Número primo


En matemáticas, un número primo es un número natural mayor que 1 que tiene únicamente dos divisores positivos distintos: él mismo y el 1.[1] Por el contrario, los números compuestos son los números naturales que tienen algún divisor natural aparte de sí mismos y del 1, y, por lo tanto, pueden factorizarse. El número 1, por convenio, no se considera ni primo ni compuesto.
Los 168 números primos menores que 1000 son:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991 y 997 (sucesión A000040 en OEIS).
El primer número primo a partir del número mil es el 1009, después de diez mil es el 10 007, a partir de cien mil es el 100 003 e inmediatamente tras un millón es el 1 000 003.
La propiedad de ser número primo se denomina primalidad.
En la teoría algebraica de números, los números primos se denominan números racionales primos para distinguirlos de los números gaussianos primos.[2] La primalidad no depende del sistema de numeración, pero sí del anillo donde se estudia la primalidad. Dos es primo racional; sin embargo tiene factores como entero gaussiano: 2 = (1+i)*(1-i).
El estudio de los números primos es una parte importante de la teoría de números, rama de las matemáticas que trata las propiedades, básicamente aritméticas,[3] de los números enteros.
Los números primos están presentes en algunas conjeturas centenarias tales como la hipótesis de Riemann y la conjetura de Goldbach, resuelta por Harald Helfgott en su forma débil.
La distribución de los números primos es un asunto reiterativo de investigación en la teoría de números: si se consideran números aisladamente, los primos parecieran estar distribuidos de modo probabilístico, pero la distribución «global» de los números primos se ajusta a leyes bien definidas.
Historia[editar]
El Oriente prehelénico[editar]

Las muescas presentes en el hueso de Ishango, que data de hace más de 20 000 años (anterior por tanto a la aparición de la escritura) y que fue hallado por el arqueólogo Jean de Heinzelin de Braucourt,[4] parecen aislar cuatro números primos: 11, 13, 17 y 19. Algunos arqueólogos interpretan este hecho como la prueba del conocimiento de los números primos. Con todo, existen muy pocos hallazgos que permitan discernir los conocimientos que tenía realmente el hombre de aquella época.[5]
Numerosas tablillas de arcilla cocida atribuidas a las civilizaciones que se fueron sucediendo en Mesopotamia a lo largo del II milenio a. C. muestran la resolución de problemas aritméticos y atestiguan los conocimientos de la época. Los cálculos requerían conocer los inversos de los naturales, que también se han hallado en tablillas.[6] En el sistema sexagesimal que empleaban los babilonios para escribir los números, los inversos de los divisores de potencias de 60 (números regulares) se calculan fácilmente; por ejemplo, dividir entre 24 equivale a multiplicar por 150 (2·60+30) y correr la coma sexagesimal dos lugares. El conocimiento matemático de los babilonios necesitaba una sólida comprensión de la multiplicación, la división y la factorización de los naturales.
En las matemáticas egipcias, el cálculo de fracciones requería conocimientos sobre las operaciones, la división de naturales y la factorización. Los egipcios solo operaban con las llamadas fracciones egipcias, suma de fracciones unitarias, es decir, aquellas cuyo numerador es 1, como , por lo que las fracciones de numerador distinto de 1 se escribían como suma de inversos de naturales, a ser posible sin repetición en lugar de .[7] Es por ello que, en cierta manera, tenían que conocer o intuir los números primos.[8]
Antigua Grecia[editar]

La primera prueba indiscutible del conocimiento de los números primos se remonta a alrededor del año 300 a. C. y se encuentra en los Elementos de Euclides (tomos VII a IX). Euclides define los números primos, demuestra que hay infinitos de ellos, define el máximo común divisor y el mínimo común múltiplo y proporciona un método para determinarlos que hoy en día se conoce como el algoritmo de Euclides. Los Elementos contienen asimismo el teorema fundamental de la aritmética y la manera de construir un número perfecto a partir de un número primo de Mersenne.
La criba de Eratóstenes, atribuida a Eratóstenes de Cirene, es un método sencillo que permite encontrar números primos. Hoy en día, empero, los mayores números primos que se encuentran con la ayuda de ordenadores emplean otros algoritmos más rápidos y complejos.
Desde la época del Renacimiento[editar]

Después de las matemáticas griegas hubo pocos avances en el estudio de los números primos hasta el siglo xvii. En 1640 Pierre de Fermat estableció (aunque sin demostración) el pequeño teorema de Fermat, posteriormente demostrado por Leibniz y Euler. Es posible que mucho antes se conociera un caso especial de dicho teorema en China.
Fermat conjeturó que todos los números de la forma 22n+1 eran primos (debido a lo cual se los conoce como números de Fermat) y verificó esta propiedad hasta n = 4 (es decir, 216 + 1). Sin embargo, el número de Fermat 232 + 1 es compuesto (uno de sus factores primos es 641), como demostró Euler. De hecho, hasta nuestros días no se conoce ningún número de Fermat que sea primo aparte de los que ya conocía el propio Fermat.
El monje francés Marin Mersenne investigó los números primos de la forma 2p − 1, con p primo. En su honor, se los conoce como números de Mersenne.
En el trabajo de Euler en teoría de números se encuentran muchos resultados que conciernen a los números primos. Demostró la divergencia de la serie , y en 1747 demostró que todos los números perfectos pares son de la forma 2p-1(2p - 1), donde el segundo factor es un número primo de Mersenne. Se cree que no existen números perfectos impares, pero todavía es una cuestión abierta.
A comienzos del siglo xix, Legendre y Gauss conjeturaron de forma independiente que, cuando n tiende a infinito, el número de primos menores o iguales que n es asintótico a , donde ln(n) es el logaritmo natural de n. Las ideas que Bernhard Riemann plasmó en un trabajo de 1859 sobre la función zeta describieron el camino que conduciría a la demostración del teorema de los números primos. Hadamard y De la Vallée-Poussin, cada uno por separado, dieron forma a este esquema y consiguieron demostrar el teorema en 1896.
Actualmente no se comprueba la primalidad de un número por divisiones sucesivas, al menos no si el número es relativamente grande.
Durante el siglo xix se desarrollaron algoritmos para saber si un número es primo o no factorizando completamente el número siguiente (p+1) o el anterior (p-1). Dentro del primer caso se encuentra el test de Lucas-Lehmer, desarrollado a partir de 1856. Dentro del segundo caso se encuentra el test de Pépin para los números de Fermat (1877). El caso general de test de primalidad cuando el número inmediatamente anterior se encuentra completamente factorizado se denomina test de Lucas.
Posteriormente se encontraron algoritmos de primalidad con solo obtener una factorización parcial de p+1 o p-1. Ejemplos de estos algoritmos son el test de Proth (desarrollado alrededor de 1878) y el test de Pocklington (1914). En estos algoritmos se requiere que el producto de los factores primos conocidos de p-1 sea mayor que la raíz cuadrada de p. Más recientemente, en 1975, Brillhart, Lehmer y Selfridge desarrollaron el test de primalidad BLS que solo requiere que dicho producto sea mayor que la raíz cúbica de p. El mejor método conocido de esta clase es el test de Koniaguin y Pomerance del año 1997, que requiere que dicho producto sea mayor que p3/10.[9][10]
A partir de la década de 1970 varios investigadores descubrieron algoritmos para determinar si cualquier número es primo o no con complejidad subexponencial, lo que permite realizar tests en números de miles de dígitos, aunque son mucho más lentos que los métodos anteriores. Ejemplos de estos algoritmos son el test APRT-CL (desarrollado en 1979 por Adleman, Pomerance y Rumely, con mejoras introducidas por Cohen y Lenstra en 1984), donde se usan los factores de pm-1, donde el exponente m depende del tamaño del número cuya primalidad se desea verificar, el test de primalidad por curvas elípticas (desarrollado en 1986 por S. Goldwasser, J. Kilian y mejorado por A. O. L. Atkin), que entrega un certificado consistente en una serie de números que permite después confirmar rápidamente si el número es primo o no. El desarrollo más reciente es el test de primalidad AKS (2002), que si bien su complejidad es polinómica, para los números que puede manejar la tecnología actual es el más lento de los tres.
Durante mucho tiempo, se pensaba que la aplicación de los números primos era muy limitada fuera de la matemática pura.[11][12] Esto cambió en los años 1970 con el desarrollo de la criptografía de clave pública, en la que los números primos formaban la base de los primeros algoritmos, tales como el algoritmo RSA.
Desde 1951, el mayor número primo conocido siempre ha sido descubierto con la ayuda de ordenadores. La búsqueda de números primos cada vez mayores ha suscitado interés incluso fuera de la comunidad matemática. En los últimos años han ganado popularidad proyectos de computación distribuida tales como el GIMPS, mientras los matemáticos siguen investigando las propiedades de los números primos.
El número 1 no se considera primo[editar]
La cuestión acerca de si el número 1 debe o no considerarse primo está basada en la convención. Ambas posturas tienen sus ventajas y sus inconvenientes. De hecho, hasta el siglo xix, los matemáticos en su mayoría lo consideraban primo. Muchos trabajos matemáticos siguen siendo válidos a pesar de considerar el 1 como un número primo, como, por ejemplo, el de Stern y Zeisel. La lista de Derrick Norman Lehmer de números primos hasta el 10.006.721, reimpresa hasta el año 1956[13] empezaba con el 1 como primer número primo.[14]
Actualmente, la comunidad matemática se inclina por no considerar al 1 en la lista de los números primos. Esta convención, por ejemplo, permite una formulación muy económica del teorema fundamental de la aritmética: «todo número natural tiene una representación única como producto de factores primos, salvo el orden».[15][16] Además, los números primos tienen numerosas propiedades de las que carece el 1, tales como la relación del número con el valor correspondiente de la función φ de Euler o la función divisor.[17] Cabe también la igualdad para todo entero positivo, , lo que permitiría decir que tiene factores.[18]
Propiedades de los números primos[editar]
Teorema fundamental de la aritmética[editar]
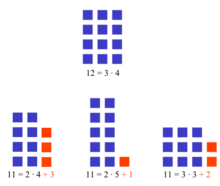
El teorema fundamental de la aritmética establece que todo número natural tiene una representación única como producto de factores primos, salvo el orden. Un mismo factor primo puede aparecer varias veces. El 1 se representa entonces como un producto vacío.
Se puede considerar que los números primos son los «ladrillos» con los que se construye cualquier número natural. Por ejemplo, se puede escribir el número 23.244 como producto de 22·3·13·149, y cualquier otra factorización del 23.244 como producto de números primos será idéntica excepto por el orden de los factores.
La importancia de este teorema es una de las razones para excluir el 1 del conjunto de los números primos. Si se admitiera el 1 como número primo, el enunciado del teorema requeriría aclaraciones adicionales.
A partir de esta unicidad en la factorización en factores primos se desarrollan otros conceptos muy utilizados en matemáticas, tales como el mínimo común múltiplo, el máximo común divisor y la coprimalidad de dos o más números. Así,
- El mínimo común múltiplo de dos o más números es el menor de los múltiplos comunes de todos ellos. Para calcularlo, se descomponen los números en factores primos y se toman los factores comunes y no comunes con su máximo exponente. Por ejemplo, el mínimo común múltiplo de 10=2·5 y 12=22·3 es 60=22·3·5.
- El máximo común divisor de dos o más números es el mayor de los divisores comunes de todos ellos. Es igual al producto de los factores comunes con su mínimo exponente. En el ejemplo anterior, el máximo común divisor de 10 y 12 es 2.
- Finalmente, dos o más números son coprimos, o primos entre sí, si no tienen ningún factor primo común; es decir, si su máximo común divisor es 1. Un número primo es, así, coprimo con cualquier número natural que no sea múltiplo de él mismo.
Otras propiedades[editar]
- En su escritura en el sistema de numeración decimal, todos los números primos, salvo el 2 y el 5, tiene como el guarismo de las unidades uno de estos: 1, 3, 7 o 9. En general, en cualquier sistema de numeración, todos los números primos salvo un número finito acaban en una cifra que es coprima con la base.
- De lo anterior se deduce que todos los números primos salvo el 2 son de la forma 4n + 1 o bien 4n + 3. Igualmente, todos los números primos salvo el 2 y el 3 son de la forma 6n + 1 o 6n - 1.
- En la progresión aritmética 3, 7, 11, 15, 19, 23, 27, 31, …, hay una cantidad infinita de números primos de la forma 4n-1, n natural.[19]
- En la progresión aritmética 7, 13, 19, 25, 31, 37, 43, 49, 55, 61, 67, …, hay una cantidad infinita de números primos de la forma 6k+1, k natural.[20]
- Lema de Euclides: Si p es un número primo y divisor del producto de números enteros ab, entonces p es divisor de a o de b.
- Pequeño teorema de Fermat: Si p es primo y a es algún número natural diferente de 1, entonces ap - a es divisible por p.
- Si un número p no divide al número m, entonces (p; m) =1[21]
- Si p es primo distinto de 2 y 5, siempre es un número periódico en su representación decimal, de periodo p − 1 o un divisor de p − 1. Esto se puede deducir directamente a partir del pequeño teorema de Fermat. expresado en base q (en lugar de en base 10) tiene propiedades similares, siempre que p no sea un factor primo de q.
- Teorema de Wilson: Un número natural n > 1 es primo si y solo si el factorial (n - 1)! + 1 es divisible por n. Asimismo, un número natural n > 4 es compuesto si y solo si (n - 1)! es divisible por n.
- La característica de todo cuerpo es, o bien cero, o bien un número primo.
- Primer teorema de Sylow: Si G es un grupo finito, p primo y pn es la mayor potencia de p que divide el orden de G. Entonces, existe un subgrupo de G de orden pn.
- Teorema de Cauchy: Si G es un grupo finito y p es un número primo que divide al orden de G, entonces G contiene un elemento de orden p.
- La constante de Copeland-Erdős 0,235711131719232931374143…, obtenida por concatenación de los números primos en el sistema decimal, es un número irracional.
- El valor de la función zeta de Riemann en cada punto del plano complejo se da como una continuación meromorfa de una función definida por un producto sobre el conjunto de todos los primos para Re(s) > 1:
- En la región donde es convergente, este producto indexado por los números primos se puede calcular, obteniéndose diversos valores, algunos de ellos importantes en teoría de números. Los dos primeros son:
- (correspondiente a la serie armónica, relacionado con la infinitud de números primos).
- (correspondiente al problema de Basilea).
- En general es un número racional cuando n es un número entero positivo par.
- El anillo es un cuerpo si y solo si p es primo. Equivalentemente: p es primo si y solo si φ(p) = p − 1.
- Si p > 1, el polinomio x p-1+x p-2+ ··· + 1 es irreducible sobre si y solo si p es primo.
- Un número natural n es primo si y solo si el n-ésimo polinomio de Chebyshov de la primera especie Tn(x), dividido entre x, es irreducible en . Además, Tn(x) ≡ xn si y solo si n es primo.
- No todo número primo es un número gaussiano primo; tal el caso de 2, que como entero gaussiano admite la descomposición don de la norma de es 2, por lo tanto no es unidad en Z[i].
- Los números primos de la forma son igual a la suma de dos cuadrados perfectos; por lo que no son números gaussianos primos. En tanto que los números primos de la forma sí son números gaussianos primos.
- Todo número racional primo es un número gaussiano entero, sin ser necesariamente número gaussiano primo.[22]
Números primos y funciones aritméticas[editar]
Las funciones aritméticas, es decir, funciones reales o complejas, definidas sobre un conjunto de números naturales, desempeñan un papel crucial en la teoría de números. Las más importantes son las funciones multiplicativas, que son aquellas funciones f en las cuales, para cada par de números coprimos (a,b) se tiene
- .
Algunos ejemplos de funciones multiplicativas son la función φ de Euler, que a cada n asocia el número de enteros positivos menores y coprimos con n, y las funciones τ y σ, que a cada n asocian respectivamente el número de divisores de n y la suma de todos ellos. El valor de estas funciones en las potencias de números primos es
- ,
- ,
- .
Gracias a la propiedad que las define, las funciones aritméticas pueden calcularse fácilmente a partir del valor que toman en las potencias de números primos. De hecho, dado un número natural n de factorización
se tiene que
con lo que se ha reconducido el problema de calcular f(n) al de calcular f sobre las potencias de los números primos que dividen n, valores que son generalmente más fáciles de obtener mediante una fórmula general. Por ejemplo, para conocer el valor de la función φ sobre n=450=2·32·52 basta con calcular
- .
Características del conjunto de los números primos[editar]
Infinitud de los números primos[editar]
Existen infinitos números primos. Euclides realizó la primera demostración alrededor del año 300 a. C. en el libro IX de su obra Elementos.[23] Una adaptación común de esta demostración original sigue así: Se toma un conjunto arbitrario pero finito de números primos p1, p2, p3, ···, pn, y se considera el producto de todos ellos más uno, . Este número es obviamente mayor que 1 y distinto de todos los primos pi de la lista. El número q puede ser primo o compuesto. Si es primo tendremos un número primo que no está en el conjunto original. Si, por el contrario, es compuesto, entonces existirá algún factor p que divida a q. Suponiendo que p es alguno de los pi, se deduce entonces que p divide a la diferencia , pero ningún número primo divide a 1, es decir, se ha llegado a un absurdo por suponer que p está en el conjunto original. La consecuencia es que el conjunto que se escogió no es exhaustivo, ya que existen números primos que no pertenecen a él, y esto es independiente del conjunto finito que se tome.
Por tanto, el conjunto de los números primos es infinito.
Si se toma como conjunto el de los n primeros números primos, entonces , donde pn# es lo que se llama primorial de pn. Un número primo de la forma pn# +1 se denomina número primo de Euclides en honor al matemático griego. También se puede elaborar una demostración similar a la de Euclides tomando el producto de un número dado de números primos menos uno, el lugar del producto de esos números primos más uno. En ese sentido, se denomina número primo primorial a un número primo de la forma pn# ± 1.
No todos los números de la forma pn# +1 son primos. En este caso, como se sigue de la demostración anterior, todos los factores primos deberán ser mayores que n. Por ejemplo: 2·3·5·7·11·13+1=30031=59·509
Otros matemáticos han demostrado la infinitud de los números primos con diversos métodos procedentes de áreas de las matemáticas tales como al álgebra conmutativa y la topología.[24] Algunas de estas demostraciones se basan en el uso de sucesiones infinitas con la propiedad de que cada uno de sus términos es coprimo con todos los demás, por lo que se crea una biyección entre los términos de la sucesión y un subconjunto (infinito) del conjunto de los primos.
Una sucesión que cumple dicha propiedad es la sucesión de Euclides-Mullin, que deriva de la demostración euclídea de la infinitud de los números primos, ya que cada uno de sus términos se define como el factor primo más pequeño de uno más el producto de todos los términos anteriores. La sucesión de Sylvester se define de forma similar, puesto que cada uno de sus términos es igual a uno más el producto de todos los anteriores. Aunque los términos de esta última sucesión no son necesariamente todos primos, cada uno de ellos es coprimo con todos los demás, por lo que se puede escoger cualquiera de sus factores primos, por ejemplo, el menor de ellos, y el conjunto resultante será un conjunto infinito cuyos términos son todos primos.
Otros enunciados que implican la infinitud de los números primos[editar]
Un resultado aún más fuerte, y que implica directamente la infinitud de los números primos, fue descubierto por Euler en el siglo xviii. Establece que la serie es divergente. Uno de los teoremas de Mertens concreta más, estableciendo que
- [25]
donde la expresión O(1) indica que ese término está acotado entre -C y C para n mayor que n0, donde los valores de C y n0 no están especificados.[26]
Otro resultado es el teorema de Dirichlet, que dice así:
|
El postulado de Bertrand enuncia así:
|
Una manera más débil pero elegante de formularlo es que, si n es un número natural mayor que 1, entonces siempre existe un número primo p tal que n < p < 2n. Esto supone que, en una progresión geométrica de primer término entero mayor que 3 y razón igual a 2, entre cada término de la progresión y el siguiente, se tiene al menos un número primo.
Frecuencia de los números primos[editar]
10 4 −0,3 2,2 2,500 102 25 3,3 5,1 4,000 103 168 23 10 5,952 104 1.229 143 17 8,137 105 9.592 906 38 10,425 106 78.498 6.116 130 12,740 107 664.579 44.158 339 15,047 108 5.761.455 332.774 754 17,357 109 50.847.534 2.592.592 1.701 19,667 1010 455.052.511 20.758.029 3.104 21,975 1011 4.118.054.813 169.923.159 11.586 24,283 … … … … …

Una vez demostrado la infinitud de los números primos, cabe preguntarse cómo se distribuyen los primos entre los números naturales, es decir, cuán frecuentes son y dónde se espera encontrar el n-ésimo número primo. Este estudio lo iniciaron Gauss y Legendre de forma independiente a finales del siglo xviii, para el cual introdujeron la función enumerativa de los números primos π(n), y conjeturaron que su valor fuese aproximadamente
- .[27]
El empeño de demostrar esta conjetura abarcó todo el siglo xix. Los primeros resultados fueron obtenidos entre 1848 y 1859 por Chebyshov, quien demostró utilizando métodos puramente aritméticos la existencia de dos constantes A y B tales que
para n suficientemente grande. Consiguió demostrar que, si existía el límite del cociente de aquellas expresiones, este debía ser 1.
Hadamard y De la Vallée-Poussin elaboraron una demostración en 1896, independientemente el uno del otro, usando métodos similares, basados en el uso de la función zeta de Riemann, que había sido introducida por Bernhard Riemann en 1859. Hubo que esperar hasta 1949 para encontrar una demostración que usara solo métodos elementales (es decir, sin usar el análisis complejo). Esta demostración fue ideada por Selberg y Erdős. Actualmente, se conoce el teorema como teorema de los números primos.
El mismo Gauss introdujo una estimación más precisa, utilizando la función logaritmo integral:
- .
En 1899 De la Vallée-Poussin demostró que el error que se comete aproximando de esta forma es
para una constante positiva a y para cada entero m. Este resultado fue ligeramente mejorado a lo largo de los años. Por otra parte, en 1901 Von Koch mostró que si la hipótesis de Riemann era cierta, se tenía la siguiente estimación, más precisa:[28]
Una forma equivalente al teorema de los números primos es que pn, el n-ésimo número primo, queda bien aproximado por nln(n). En efecto, pn es estrictamente mayor que este valor.
Diferencia entre dos primos consecutivos[editar]
Ligado a la distribución de los números primos se encuentra el estudio de los intervalos entre dos primos consecutivos. Este intervalo, con la única salvedad del que hay entre el 2 y el 3, debe ser siempre igual o mayor que 2, ya que entre dos números primos consecutivos al menos hay un número par y por tanto compuesto. Si dos números primos tienen por diferencia 2, se dice que son gemelos, y con la salvedad del «triplete» formado por los números 3, 5 y 7, los números gemelos se presentan siempre de dos en dos. Esto también es fácil de demostrar: entre tres números impares consecutivos mayores que 3 siempre hay uno que es múltiplo de 3, y por tanto compuesto. Los primeros pares de números primos gemelos son (3,5), (5,7), (11, 13), (17, 19) y (29, 31).
Por otra parte, la diferencia entre primos consecutivos puede ser tan grande como se quiera. La demostración es relativamente sencilla:
Sea un número natural . Entonces, todos los números de la forma
son números compuestos si , pues y .
Se puede construir así una lista con números compuestos, y dado que es un número natural arbitrario, entonces el intervalo puede hacerse tan grande como se desee.
Por ejemplo, si se requiere construir un intervalo de cinco números consecutivos donde ninguno sea un número primo, se hace . Estos valores corresponden a:
El siguiente valor, 6!+7=727, es primo.[29] De todas formas, el menor número primo que dista del siguiente en n es generalmente mucho menor que el factorial, por ejemplo, el caso más pequeño de dos primos consecutivos separados de ocho unidades es (89, 97), mientras que 8! es igual a 40.320.
La sucesión de las diferencias entre primos consecutivos[30] ha sido profusamente estudiada en matemáticas, y alrededor de este concepto se han establecido muchas conjeturas que permanecen sin resolver.
Conclusión[editar]


El modelado de la distribución de los números primos es un tema de investigación recurrente entre los teóricos de números. La primalidad de un número concreto es (hasta ahora) impredecible a pesar de que existen leyes, como el teorema de los números primos y el postulado de Bertrand, que gobiernan su distribución a gran escala. Leonhard Euler comentó:
Hasta el día de hoy, los matemáticos han intentado en vano encontrar algún orden en la sucesión de los números primos, y tenemos motivos para creer que es un misterio en el que la mente jamás penetrará.[31]
En una conferencia de 1975, el matemático germano-estadounidense Don Zagier comentó:
Hay dos hechos sobre la distribución de los números primos de los que espero convencerles de forma tan incontestable que quedarán permanentemente grabados en sus corazones. El primero es que, a pesar de su definición simple y del papel que desempeñan como ladrillos con los que se construyen los números naturales, los números primos crecen como malas hierbas entre los números naturales, y no parecen obedecer ninguna otra ley que la del azar, y nadie puede predecir dónde brotará el siguiente. El segundo hecho es aún más asombroso, ya que dice justo lo contrario: que los números primos muestran una regularidad pasmosa, que hay leyes que gobiernan su comportamiento, y que obedecen estas leyes con precisión casi militar.[32]
Encontrar números primos[editar]
Tests de primalidad[editar]

La criba de Eratóstenes es una manera sencilla de hallar todos los números primos menores o iguales que un número dado. Se basa en confeccionar una lista de todos los números naturales desde el 2 hasta ese número y tachar repetidamente los múltiplos de los números primos ya descubiertos. La criba de Atkin, más moderna, tiene una mayor complejidad, pero si se optimiza apropiadamente también es más rápida. También existe una reciente criba de Sundaram que genera únicamente números compuestos, siendo los primos los números faltantes.
En la práctica, lo que se desea es determinar si un número dado es primo sin tener que confeccionar una lista de números primos. Un método para determinar la primalidad de un número es la división por tentativa, que consiste en dividir sucesivamente ese número entre los números primos menores o iguales a su raíz cuadrada. Si alguna de las divisiones es exacta, entonces el número no es primo; en caso contrario, es primo. Por ejemplo, dado n menor o igual que 120, para determinar su primalidad basta comprobar si es divisible entre 2, 3, 5 y 7, ya que el siguiente número primo, 11, ya es mayor que √120. Es el test de primalidad más sencillo, y rápidamente pierde su utilidad a la hora de comprobar la primalidad de números grandes, ya que el número de factores posibles crece demasiado rápido a medida que crece el número potencialmente primo.
En efecto, el número de números primos menores que n es aproximadamente
- .
De esta forma, para determinar la primalidad de n, el mayor factor primo que se necesita no es mayor que √n, dejando el número de candidatos a factor primo en cerca de
- .
Esta expresión crece cada vez más lentamente en función de n, pero, como los n grandes son de interés, el número de candidatos también se hace grande: por ejemplo, para n = 1020 se tienen 450 millones de candidatos.
Asimismo, existen otros muchos tests de primalidad deterministas que se basan en propiedades que caracterizan a los números primos, pero su utilidad computacional depende mucho del test usado. Por ejemplo, se podría emplear el teorema de Wilson para calcular la primalidad de un número, pero tiene el inconveniente de requerir el cálculo de un factorial, una operación computacionalmente prohibitiva cuando se manejan números grandes. Aquí entra en juego el tiempo de ejecución del algoritmo empleado, que se expresa en la notación de Landau. Para poder determinar la primalidad de números cada vez más grandes (de miles de cifras) se buscan aquellos algoritmos cuyo tiempo de ejecución crezca lo más lentamente posible, a ser posible, que se pueda expresar como un polinomio. Si bien el test de primalidad AKS cumple con esta condición, para el rango de números que se usa en la práctica este algoritmo es extremadamente lento.
Por otra parte, a menudo basta con tener una respuesta más rápida con una alta probabilidad (aunque no segura) de ser cierta. Se puede comprobar rápidamente la primalidad de un número relativamente grande mediante tests de primalidad probabilísticos. Estos tests suelen tomar un número aleatorio llamado "testigo" e introducirlo en una fórmula junto con el número potencialmente primo n. Después de varias iteraciones, se resuelve que n es "definitivamente compuesto" o bien "probablemente primo". Estos últimos números pueden ser primos o bien pseudoprimos (números compuestos que pasan el test de primalidad). Algunos de estos tests no son perfectos: puede haber números compuestos que el test considere "probablemente primos" independientemente del testigo utilizado. Esos números reciben el nombre de pseudoprimos absolutos para ese test. Por ejemplo, los números de Carmichael son números compuestos, pero el test de Fermat los evalúa como probablemente primos. Sin embargo, los tests probabilísticos más utilizados, como el test de Miller-Rabin o el obsoleto test de Solovay-Strassen, superado por el anterior, no tienen este inconveniente, aun siendo igualmente tests probabilísticos.
Algunos tests probabilísticos podrían pasar a ser determinísticos y algunos tests pueden mejorar su tiempo de ejecución si se verifican algunas hipótesis matemáticas. Por ejemplo, si se verifica la hipótesis generalizada de Riemann, se puede emplear una versión determinística del test de Miller-Rabin, y el test de primalidad por curvas elípticas podría mejorar notablemente su tiempo de ejecución si se verificaran algunas hipótesis de teoría analítica de números.
Algoritmos de factorización[editar]
Un algoritmo de factorización es un algoritmo que separa uno a uno los factores primos de un número. Los algoritmos de factorización pueden funcionar también a modo de tests de primalidad, pero en general tienen un tiempo de ejecución menos ventajoso. Por ejemplo, se puede modificar el algoritmo de división por tentativa de forma que no se detenga cuando se obtenga una división exacta, sino que siga realizando nuevas divisiones, y no sobre el número original, sino sobre el cociente obtenido. Después de la división por tentativa, los métodos más antiguos que se conocen son el método de Fermat, que se basa en las diferencias entre cuadrados y que es especialmente eficaz cuando n es el producto de dos números primos próximos entre sí, y el método de Euler, que se basa en la representación de n como suma de dos cuadrados de dos formas distintas.
Más recientemente, se han elaborado algoritmos basados en una gran variedad de técnicas, como las fracciones continuas o las curvas elípticas, aunque algunos son mejoras de métodos anteriores (la criba cuadrática, por ejemplo, se basa en una mejora del método de Fermat y posee complejidad computacional subexponencial sobre el número de cifras de n). Otros, como el método rho de Pollard, son probabilísticos, y no garantizan hallar los divisores de un número compuesto.
Hoy por hoy, el algoritmo determinístico más rápido de uso general es la criba general del cuerpo de números (GNFS por las siglas de su nombre en inglés: General number field sieve), que también posee complejidad computacional subexponencial sobre el número de cifras de n.[33] Se ha propuesto un algoritmo cuyo tiempo de ejecución es polinómico sobre el número de cifras de n (el algoritmo de Shor), pero requiere ser ejecutado en un ordenador cuántico, ya que su simulación en un ordenador normal requiere un tiempo exponencial. No se conocen algoritmos para factorizar en una computadora tradicional en tiempo polinómico y tampoco se demostró que esto sea imposible.
Fórmulas que solo generasen números primos[editar]
A lo largo de la historia, se han buscado numerosas fórmulas para generar los números primos. El nivel más alto de exigencia para una fórmula así sería que asociara a cada número natural n el n-ésimo número primo. De forma más indulgente, se puede pedir una función f inyectiva que asocie a cada número natural n un número primo de tal forma que cada uno de los valores tomados aparezca solo una vez.
Además, se exige que la función se pueda aplicar, efectiva y eficazmente, en la práctica.[34] Por ejemplo, el teorema de Wilson asegura que p es un número primo si y solo si (p-1)!≡-1 (mod p). Otro ejemplo: la función f(n) = 2 + ( 2(n!) mod (n+1)) genera todos los números primos, solo los números primos, y solo el valor 2 se toma más de una vez. Sin embargo, ambas fórmulas se basan en el cálculo de un factorial, lo que las hace computacionalmente inviables.
En la búsqueda de estas funciones, se han investigado, notablemente, las funciones polinómicas. Cabe subrayar que ningún polinomio, aun en varias variables, devuelve solo valores primos.[35] Por ejemplo, el polinomio en una variable f(n) = n² + n + 41, estudiada por Leonardo Euler, devuelve valores primos para n = 0, …, 39, sin embargo para n= 40, resulta un número compuesto.[36] Si el término constante vale cero, entonces el polinomio es múltiplo de n, por lo que el polinomio es compuesto para valores compuestos de n. En caso contrario, si c es el término constante, entonces f(cn) es múltiplo de c, por lo que si el polinomio no es constante, necesariamente deberá incluir valores compuestos.
Sin embargo, hay polinomios en varias variables cuyos valores positivos (cuando las variables recorren números naturales) son precisamente números primos. Un ejemplo, es este polinomio descubierto por Jones, Sato, Wada y Wiens en 1976:[35]
Al igual que ocurre con las fórmulas con factoriales, este polinomio no es práctico de calcular, ya que, aunque los valores positivos que toma son todos primos, prácticamente no devuelve otra cosa que valores negativos cuando se hacen variar las variables a a z de 0 a infinito.
Otro enfoque al problema de encontrar una función que solo genere números primos viene dado a partir del teorema de Mills, que indica que existe una constante θ tal que
es siempre un número primo, donde es la función piso.[37] Todavía no se conoce ninguna fórmula para calcular la constante de Mills, y las aproximaciones que se emplean en la actualidad se basa en la sucesión de los así llamados números primos de Mills (los números primos generados mediante esta fórmula), que no pueden ser obtenidos rigurosamente, sino solo de manera probabilística, suponiendo cierta la hipótesis de Riemann.
Clases de números primos[editar]
De mayor interés son otras fórmulas que, aunque no solo generen números primos, son más rápidas de implementar, sobre todo si existe un algoritmo especializado que permita calcular rápidamente la primalidad de los valores que van tomando. A partir de estas fórmulas se obtienen subconjuntos relativamente pequeños del conjunto de los números primos, que suelen recibir un nombre colectivo.
Primos primoriales y primos factoriales[editar]
Los números primos primoriales, directamente relacionados con la demostración euclidiana de la infinitud de los números primos, son los de la forma p = n# ± 1 para algún número natural n, donde n# es igual al producto 2 · 3 · 5 · 7 · 11 · … de todos los primos ≤ n. Asimismo, un número primo se dice primo factorial si es de la forma n! ± 1. Los primeros primos factoriales son:
- n! − 1 es primo para n = 3, 4, 6, 7, 12, 14, 30, 32, 33, 38, 94, 166, 324, …[38]
- n! + 1 es primo para n = 0, 1, 2, 3, 11, 27, 37, 41, 73, 77, 116, 154, 320, …[39]
Números primos de Fermat[editar]

Los números de Fermat, ligados a la construcción de polígonos regulares con regla y compás, son los números de la forma , con n natural. Los únicos números primos de Fermat que se conocen hasta la fecha son los cinco que ya conocía el propio Fermat, correspondientes a n = 0, 1, 2, 3 y 4, mientras que para valores de n entre 5 y 32 estos números son compuestos.[40]
Para determinar su primalidad, existe un test especializado cuyo tiempo de ejecución es polinómico: el test de Pépin. Sin embargo, los propios números de Fermat crecen tan rápidamente que solo se lo ha podido aplicar para valores de n pequeños. En 1999 se lo aplicó para n = 24. Para determinar el carácter de otros números de Fermat mayores se utiliza el método de divisiones sucesivas y de esa manera a fecha de junio de 2009 se conocen 241 números de Fermat compuestos, aunque en la mayoría de los casos se desconozca su factorización completa.[40]
Números primos de Mersenne[editar]
Los números de Mersenne son los de forma Mp = 2p – 1, donde p es primo.[41] Los mayores números primos conocidos son generalmente de esta forma, ya que existe un test de primalidad muy eficaz, el test de Lucas-Lehmer, para determinar si un número de Mersenne es primo o no.
Actualmente, el mayor número primo que se conoce es M82 589 933 = 282 589 933 - 1, que tiene 24 862 048 cifras en el sistema decimal. Se trata cronológicamente del 51.er número primo de Mersenne conocido y su descubrimiento se anunció el 7 de diciembre de 2018[42] gracias al proyecto de computación distribuida «Great Internet Mersenne Prime Search» (GIMPS).
Otras clases de números primos[editar]
Existen literalmente decenas de apellidos que se pueden añadir al concepto de número primo para referirse a un subconjunto que cumple alguna propiedad concreta. Por ejemplo, los números primos pitagóricos son los que se pueden expresar en la forma 4n+1. Dicho de otra forma, se trata de los números primos cuyo resto al dividirlos entre 4 es 1. Otro ejemplo es el de los números primos de Wieferich, que son aquellos números primos p tales que p2 divide a 2p-1 - 1.
Algunas de estas propiedades se refieren a una relación concreta con otro número primo:
- Números primos gemelos: p y p+2 lo son si son los dos primos.
- Número primo de Sophie Germain: dado p primo, es de Sophie Germain si 2p + 1 también es primo. Una sucesión de números p1,p2,p3,··· ,pn todos ellos primos, tales que pi+1=2pi+1 para todo i ∈ {1,2,···,n-1 }, se denomina cadena (completa) de Cunningham de primera especie, y cumple por definición que cada uno de los términos, salvo el último, es un número primo de Sophie Germain. Se cree que para todo n natural existen infinitas cadenas de Cunningham de longitud n,[43] aunque hasta la fecha nadie ha proporcionado prueba de que dicha afirmación sea cierta.
- Número primo de Wagstaff: p lo es si , donde q es otro número primo.[44][45]
También se les da nombres especiales a algunas clases de primos que dependen de la base de numeración empleada o de la forma de escribir los dígitos, y no de una fórmula matemática. Es el caso de los números somirp (primos al revés), que son aquellos números primos tales que el número obtenido al invertir el orden de sus cifras también es primo. También es el caso de los números primos repunit, que son aquellos números primos que son concatenación de unos. Si, en lugar de considerarse el sistema de numeración decimal se considera el binario, se obtiene otro conjunto distinto de números primos repunit que, además, coincide con el de los números primos de Mersenne. Finalmente, los números primos triádicos son aquellos números que son primos, capicúas y simétricos respecto de una recta horizontal.
El que se le dé un nombre a una clase de números primos con una definición precisa no significa que se conozca algún número primo que sea de esa clase. Por ejemplo, no se conoce hasta el momento ningún número primo de Wall-Sun-Sun, pero su relevancia radica en que en 1992, antes de la demostración de Wiles del último teorema de Fermat, se descubrió que la falsedad del teorema para un número primo p dado implicaba que p era un número primo de Wall-Sun-Sun. Esto hizo que, durante un tiempo, la búsqueda de números primos de esta clase fuera también la búsqueda de un contraejemplo del último teorema de Fermat.[46]
Cuadro resumen[editar]
Conjeturas[editar]
Existen numerosas preguntas abiertas acerca de los números primos. Muchas de ellas son problemas bien antiguos, y una de las más significativas es la hipótesis de Riemann, varias veces mencionada en este artículo como una conjetura que, de ser cierta, permitiría conocer numerosos resultados relevantes en diversos campos de las matemáticas.
Hipótesis de Riemann[editar]
Para entender la hipótesis de Riemann, una conjetura enunciada en 1859 pero que, hasta la fecha (2024), sigue sin resolverse, es necesario entender la función zeta de Riemann. Sea un número complejo con parte real mayor que 1. Entonces,
La segunda igualdad es una consecuencia del teorema fundamental de la aritmética, y muestra que la función zeta está íntimamente relacionada con los números primos.
Existen dos tipos de ceros de la función zeta, es decir, valores s para los cuales ζ(s) = 0: los triviales, que son s=-2, s=-4, s=-6, etc., (los enteros pares negativos) y los no triviales, que son aquellos ceros que no se encuentran en el eje real. Lo que indica la hipótesis de Riemann es que la parte real de todos los ceros no triviales es igual a 1/2.
La veracidad de la hipótesis implica una profunda conexión con los números primos, en esencia, en el caso de verificarse, dice que los números primos están distribuidos de la forma más regular posible. Desde un punto de vista «físico», dice grosso modo que las irregularidades en la distribución de los números primos solo proceden de ruido aleatorio. Desde un punto de vista matemático, dice que la distribución asintótica de los números primos (según el teorema de los números primos, la proporción de primos menores que n es ) también es cierta para intervalos mucho menores, con un error de aproximadamente la raíz cuadrada de n (para intervalos próximos a n). Está ampliamente extendido en la comunidad matemática que la hipótesis sea cierta. En concreto, la presunción más simple es que los números primos no deberían tener irregularidades significativas en su distribución sin una buena razón.[47]
Otras conjeturas[editar]
Infinitud de ciertos tipos de números primos[editar]
Muchas conjeturas tratan sobre si hay infinitos números primos de una determinada forma. Así, se conjetura que hay infinitos números primos de Fibonacci[48] e infinitos primos de Mersenne, pero solo un número finito de primos de Fermat.[49] No se sabe si hay infinitos números primos de Euclides.
Distribución de los números primos[editar]
También hay numerosas conjeturas que se ocupan de determinadas propiedades de la distribución de los números primos. Así, la conjetura de los números primos gemelos enuncia que hay infinitos números primos gemelos, que son pares de primos cuya diferencia es de 2. La conjetura de Polignac es una versión más general y más fuerte de la anterior, ya que enuncia que, para cada entero positivo n, hay infinitos pares de primos consecutivos que difieren en 2n. A su vez, una versión más débil de la conjetura de Polignac dice que todo número par es la diferencia de dos números primos.
Asimismo, se conjetura la infinidad de los primos de la forma n2 + 1. Según la conjetura de Brocard, entre los cuadrados de primos consecutivos mayores que 2 existen siempre al menos cuatro números primos. La conjetura de Legendre establece que, para cada n natural, existe un número primo entre n2 y (n+1)2. Finalmente, la conjetura de Cramér, cuya veracidad implicaría la de Legendre, dice que:
Teoría aditiva de números[editar]
Otras conjeturas relacionan algunas propiedades aditivas de los números con los números primos. Así, la conjetura de Goldbach dice que todo número par mayor que 2 se puede escribir como suma de dos números primos, aunque también existe una versión más débil de la misma conjetura según la cual todo número impar mayor que 5 se puede escribir como suma de tres números primos. El matemático chino Chen Jingrun demostró, en 1966, que en efecto, todo número par suficientemente grande puede expresarse como suma de dos primos o como la suma de un primo y de un número que es el producto de dos primos. ("semi-primo").[50]
Los cuatro problemas de Landau[editar]
En 1912, Landau estableció en el Quinto Congreso Internacional de Matemáticos de Cambridge una lista de cuatro de los problemas ya mencionados sobre números primos, que se conocen como los problemas de Landau. Ninguno de ellos está resuelto hasta la fecha. Se trata de la conjetura de Goldbach, la de los números primos gemelos, la de Legendre y la de los primos de la forma n2 + 1.[51]
Generalización del concepto de número primo[editar]
El concepto de número primo es tan importante que se ha visto generalizado de varias maneras en diversas ramas de las matemáticas.
Elementos primos en un anillo[editar]

Se pueden definir los elementos primos y los elementos irreducibles en cualquier dominio de integridad.[52] En cualquier dominio de factorización única, como por ejemplo, el anillo de los enteros, el conjunto de elementos primos equivale al conjunto de los elementos irreducibles, que en es {…, −11, −7, −5, −3, −2, 2, 3, 5, 7, 11, …}.
Considérense por ejemplo los enteros gaussianos , es decir, los números complejos de la forma a+bi con a, b ∈ . Este es un dominio de integridad, y sus elementos primos son los primos gaussianos. Cabe destacar que el 2 no es un primo gaussiano, porque admite factorización como producto de los primos gaussianos (1+i) y (1-i). Sin embargo, el elemento 3 sí es primo en los enteros gaussianos, pero no lo es en otro dominio entero. En general, los primos racionales (es decir, los elementos primos del anillo ) de la forma 4k+3 son primos gaussianos, pero no lo son aquellos de la forma 4k+1.
Ideales primos[editar]
En teoría de anillos, un ideal I es un subconjunto de un anillo A tal que
- si i, j ∈ I, entonces la suma i + j pertenece a I
- y si x ∈ A, i ∈ I, entonces los productos a × i, i × a pertenecen a I.
Un ideal primo se define entonces como un ideal que cumple también que:
- para cualquier par de elementos a, b del anillo A tales que su producto a × b pertenece a I, entonces, al menos uno de los dos elementos, a o b, está en I.
- I no es el anillo A entero.
Los ideales primos son una herramienta relevante en álgebra conmutativa, teoría algebraica de números y geometría algebraica. Los ideales primos del anillo de enteros son los ideales (0), (2), (3), (5), (7), (11), …
Un problema central en teoría algebraica de números es la manera en que se factorizan los ideales primos cuando se ven sometidos a una extensión de cuerpos. En el ejemplo de los enteros gaussianos, (2) se ramifica en potencia de un primo (ya que y generan el mismo ideal primo), los ideales primos de la forma son inertes (mantienen su primalidad) y los de la forma pasan a ser producto de dos ideales primos distintos.
Primos en teoría de la valoración[editar]
En teoría algebraica de números surge otra generalización más. Dado un cuerpo , reciben el nombre de valoraciones sobre determinadas funciones de en . Cada una de estas valoraciones genera una topología sobre , y se dice que dos valoraciones son equivalentes si generan la misma topología. Un primo de es una clase de equivalencia de valoraciones. Con esta definición, los primos del cuerpo de los números racionales quedan representados por la función valor absoluto así como por las valoraciones p-ádicas sobre para cada número primo p.
Nudos primos[editar]
 |
 |

| |
| Algunos nudos primos. | |||
En teoría de nudos, un nudo primo es un nudo no trivial que no se puede descomponer en dos nudos más pequeños. De forma más precisa, se trata de un nudo que no se puede escribir como suma conexa de dos nudos no triviales.
En 1949 Horst Schubert demostró un teorema de factorización análogo al teorema fundamental de la aritmética, que asegura que cada nudo se puede obtener de forma única como suma conexa de nudos primos.[53] Por este motivo, los nudos primos desempeñan un papel central en la teoría de nudos: una clasificación de los nudos ha sido desde finales del siglo xix el tema central de la teoría.
Aplicaciones en la matemática[editar]
- En el estudio de los números complejos, se acude al concepto de "primos relativos" para definir raíces primitivas de la unidad .[54] Si n es un número primo todas las raíces enésimas de 1 son raíces primitivas, salvo la raíz 1.
- En la definición de un cuerpo finito, se exige que el número de elementos de un anillo sea entero primo. En tal caso, eliminando el cero, cada elemento tiene inverso multiplicativo y se obtiene la estructura de un cuerpo.[55]
- En la definición de un polígono estrellado de n lados, para tomar los puntos de m en m, se exige que m sea menor que n/2 y primo con n.[56]
- Al definir el representante canónico de un número racional, usando clases de equivalencia de pares ordenados de números enteros, necesariamente, el par ordenado definente tiene que involucrar dos enteros primos relativos. A fortiori, por lo menos uno de ellos, un primo absoluto.[57]
Aplicaciones en la computación[editar]
El algoritmo RSA se basa en la obtención de la clave pública mediante la multiplicación de dos números grandes (mayores que 10100) que sean primos. La seguridad de este algoritmo radica en que no se conocen maneras rápidas de factorizar un número grande en sus factores primos utilizando computadoras tradicionales.
Números primos en el arte y la literatura[editar]
- Los números primos han influido en numerosos artistas y escritores. El compositor francés Olivier Messiaen se valió de ellos para crear música no métrica. En obras tales como La Nativité du Seigneur (1935) o Quatre Études de rythme (1949-50) emplea simultáneamente motivos cuya duración es un número primo para crear ritmos impredecibles. Según Messiaen, esta forma de componer fue «inspirada por los movimientos de la naturaleza, movimientos de duraciones libres y desiguales».[58]
- En la novela escrita en 1968 2001: Una Odisea Espacial, Arthur C. Clarke menciona que el monolito de origen extraterrestre tiene la proporción del cuadrado de los primeros tres números primos: 1,4,9.
- En su novela de ciencia ficción Contact, posteriormente adaptada al cine, Carl Sagan sugiere que los números primos podrían ser empleados para comunicarse con inteligencias extraterrestres, una idea que había desarrollado de manera informal con el astrónomo estadounidense Frank Drake en 1975.[59]
- El curioso incidente del perro a medianoche, de Mark Haddon, que describe en primera persona la vida de un joven autista muy dotado en matemáticas y cálculo mental, utiliza únicamente los números primos para numerar los capítulos.
- En la novela PopCo de Scarlett Thomas, la abuela de Alice Butler trabaja en la demostración de la hipótesis de Riemann. El libro ilustra una tabla de los mil primeros números primos.[60]
- La soledad de los números primos, novela escrita por Paolo Giordano, ganó el premio Strega en 2008.
- También son muchas las películas que reflejan la fascinación popular hacia los misterios de los números primos y la criptografía, por ejemplo, Cube, Sneakers, El amor tiene dos caras y Una mente maravillosa. Esta última se basa en la biografía del matemático y premio Nobel John Forbes Nash, escrita por Sylvia Nasar.[61]
- El escritor griego Apostolos Doxiadis, escribió El tío Petros y la conjetura de Goldbach, que narra cómo un ficticio matemático prodigio de principios del siglo xx se sumerge en el mundo de las matemáticas de una forma apasionante, tratando de resolver uno de los problemas más difíciles y aún no resueltos de la matemática, la conjetura de Goldbach, la cual reza: «Todo número par puede expresarse como la suma de dos números primos».
Véase también[editar]
- Criptografía
- Diferencia entre dos números primos consecutivos
- Anillo factorial
- Elemento irreducible
- Elemento primo
- Entero gaussiano
- Espiral de Ulam
- Fórmula de los números primos
- Mayor número primo conocido
- Número primo de grado industrial
- Número primo ilegal
- Primo de Solinas
- Probable primo
- Test de primalidad
- Anexo:Números primos
- Anexo:Tabla de factores primos
 Portal:Matemática. Contenido relacionado con Matemática.
Portal:Matemática. Contenido relacionado con Matemática.
|
Referencias[editar]
- ↑ Niven y Zuckerman: Introducción a la teoría , Editorial Trillas. México D. F., pág. 55
- ↑ Niven- Zuckerman. Introducción a la teoría de números
- ↑ Abramo Hefez: Curso de álgebbra vol.1, ISBN 9972-9394-1-3, pág. 87
- ↑ Marcus du Sautoy, La symphonie des nombres premiers P.42 (en francés)
- ↑ Préhistoire de la géométrie: le problème des sources, artículo de Olivier Keller (en francés)
- ↑ «Nacimiento de las matemáticas.». Archivado desde el original el 14 de junio de 2009. Consultado el 7 de junio de 2009.
- ↑ Arnaldez, Roger y otros (1988). Las antiguas ciencias del Oriente. Barcelona: Ediciones Orbis S.A. ISBN 84-402-0159-1.
- ↑ Planetmath.org. «History of prime numbers.». Archivado desde el original el 12 de diciembre de 2009. Consultado el 7 de junio de 2009.
- ↑ Crandall, Richard (2001). Prime numbers, a computational perspective. Nueva York: Springer-Verlag. ISBN 0-387-94777-9.
- ↑ Bernstein, Daniel. «Prime tests». Consultado el 1 de julio de 2009.
- ↑ Singh, Simon (1998). «Pág. 126». El enigma de Fermat. Editorial Planeta S.A. ISBN 978-84-08-02375-3..
- ↑ Carles Pina i Estany (2005). «Curiosidades sobre números primos.». Consultado el 5 de junio de 2009.
- ↑ Hans Riesel, Prime Numbers and Computer Methods for Factorization. New York: Springer (1994): 36 (en inglés)
- ↑ Richard K. Guy & John Horton Conway, The Book of Numbers. New York: Springer (1996): 129 - 130 (en inglés)
- ↑ Gowers, T (2002). Mathematics: A Very Short Introduction. Oxford University Press. p. 118. ISBN 0-19-285361-9. «La exclusión aparentemente arbitraria del 1 de la definición de número primo … no expresa ningún conocimiento profundo sobre los números: se trata simplemente de un convenio útil, adoptado para que solo haya una manera de factorizar cualquier número en sus factores primos».
- ↑ "Why is the number one not prime?" (en inglés), accedido el 31-05-2009.
- ↑ "Arguments for and against the primality of 1" (en inglés), accedido el 31-05-2009.
- ↑ Se puede probar por el principio de inducción matemática
- ↑ G.N. Berman: Un paseo por la teoría de los números, Editorial URSS, Moscú 2007, pág. 207
- ↑ Berman: Op. cit
- ↑ T. M. Aosto: Introducción a la teoría analítica de números, Editorial Reverté S.A. Barcelona, 1980
- ↑ Niven Zuckerman. Introducción a la teoría de números
- ↑ , Euclides (1991-1996). «Vol. II, libro IX, proposición 20.». Elementos. Obra completa, Madrid, Editorial Gredos. ISBN 978-84-249-1463-9.
- ↑ DiAmOnD (2008). «Demostración topológica de la infinitud de los números primos.». Consultado el 5 de junio de 2009.
- ↑ Véase, por ejemplo, An Introduction to the Theory of Numbers, p. 24. (en inglés)
- ↑ En general, en la notación de Landau, indica que está dominada asintóticamente por , es decir, . Para más información, lea notación de Landau.
- ↑ Con esta expresión se quiere decir que el límite de la razón entre las dos expresiones tiende a 1 cuando n tiende a infinito.
- ↑ von Koch, Helge (1901). «Sur la distribution des nombres premiers». SpringerLink. Consultado el 6 de junio de 2009.
- ↑ Nótese que esto no tiene por qué ser verdad en general, por ejemplo, si n es impar, se tiene que n!+(n+1) es divisible entre 2.
- ↑ (sucesión A001223 en OEIS)
- ↑ Julian Havil, Gamma: Exploring Euler's Constant (tapa dura). Princeton: Princeton University Press (2003): 163 (en inglés)
- ↑ Julian Havil, Gamma: Exploring Euler's Constant (tapa dura). Princeton: Princeton University Press (2003): 171
- ↑ Eric W. Weisstein. «Number Field Sieve» (en inglés). Consultado el 31 de mayo de 2009.
- ↑ Introducción del capítulo 3 del libro de Ribenboim The new book of prime number records.
- ↑ a b Prime Glossary - Matijasevic's Polynomial, accedido el 06-06-2009
- ↑ I.S. Sominski «Método de inducción matemática» Editorial Mir, Moscú (1985) segunda edición
- ↑ W. H. Mills, A prime-representing function (1947) (en inglés)
- ↑ (sucesión A002982 en OEIS)
- ↑ (sucesión A002981 en OEIS)
- ↑ a b Keller, Wilfrid (2009). «Fermat factoring status». Archivado desde el original el 10 de febrero de 2016. Consultado el 1 de junio de 2009.
- ↑ DiAmOnD (2008). «Todo número de Mersenne con exponente compuesto es también compuesto». Consultado el 7 de junio de 2009.. Por contraposición, se deduce que, para buscar números primos de Mersenne, basta con buscar entre los números de Mersenne con exponente primo.
- ↑ «GIMPS Project Discovers Largest Known Prime Number: 282,589,933-1». Mersenne Research, Inc. 21 de diciembre de 2018. Consultado el 21 de diciembre de 2018.
- ↑ Nicholas Anderson, Andrew J. Havens, Brian Hydefrost, Sean Murphy y Steve Sarasin. «Prime Numbers and the Riemann Hypothesis». p. 6. Archivado desde el original el 15 de junio de 2010. Consultado el 7 de junio de 2009.
- ↑ The On-Line Encyclopedia of Integer Sequences!. «A000979. Wagstaff primes.». Archivado desde el original el 18 de junio de 2010. Consultado el 23 de abril de 2010.
- ↑ Weisstein, Eric W. «Wagstaff Prime». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Caldwell, Chris. «The Prime Glossary: Wall-Sun-Sun prime» (en inglés). The Prime Pages. Universidad de Tennessee. http://primes.utm.edu/glossary/page.php?sort=WallSunSunPrime. Consultado el 6 de junio de 2009.
- ↑ Bombieri, Enrico (2000). «The Riemann hypothesis» (en inglés). Clay Mathematics Institute. Archivado desde el original el 27 de marzo de 2009. Consultado el 6 de junio de 2009.
- ↑ Caldwell, Chris. «The Top Twenty: Lucas Number» (en inglés). The Prime Pages. Universidad de Tennessee. http://primes.utm.edu/top20/page.php?id=48. Consultado el 1 de junio de 2009.
- ↑ Por ejemplo, véase Guy, Richard K. (1981), Unsolved Problems in Number Theory, Springer-Verlag., problema A3, pp. 7–8.
- ↑ Tony Crilly (2011). 50 cosas que hay que saber sobre matemáticas. Ed. Ariel. ISBN 978-987-1496-09-9.
- ↑ Mathworld - Landau's Problems (en inglés)
- ↑ «Números algebraicos». 2004. Archivado desde el original el 29 de mayo de 2009. Consultado el 7 de junio de 2009.
- ↑ En Mathworld. (en inglés)
- ↑ Kurosch. «Álgebra superior»
- ↑ Fraleig. «Álgebra abstracta»
- ↑ G.M.Bruño. «Elementos de geometría»
- ↑ C. A. Trejo «El concepto de número»
- ↑ Peter Hill (1994). Amadeus Press, ed. The Messiaen companion. ISBN 0-931340-95-0..
- ↑ Carl Pomerance, Prime Numbers and the Search for Extraterrestrial Intelligence, accedido el 31-05-2009
- ↑ A Mathematician reviews PopCo Archivado el 12 de diciembre de 2008 en Wayback Machine. (en inglés), accedido el 31-05-2009
- ↑ Music of the Spheres Archivado el 9 de octubre de 2015 en Wayback Machine., Selección de Marcus du Sautoy de películas que versan sobre los números primos (en inglés), accedido el 31-05-2009
Enlaces externos[editar]
 Wikilibros alberga un libro o manual sobre cálculo de números primos.
Wikilibros alberga un libro o manual sobre cálculo de números primos.- «Criba de Eratóstenes para buscar los números primos aplicada en C/C++». Brainum Code.
- Calculador en línea de factores primos, por www.mathstools.com
- The Prime Pages Archivado el 7 de junio de 2004 en Wayback Machine.
- Sobre el artículo de Manindra Agrawal et al. PRIMES IS IN P, en donde afirman: "We present a deterministic polynomial-time algorithm that determines whether an input number n is prime or composite" mathmistakes
- Algoritmos eficientes para calcular números primos, por Steve Litt
- ¿Es este número primo?















![{\displaystyle \mathbb {Z} [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d4da3ac703cc7721ebba91a53f6752de7157124)



















































![{\displaystyle \mathbb {Z} [i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)














