Topología

La topología (del griego τόπος, 'lugar', y λόγος, 'estudio') es la rama de la matemática dedicada al estudio de aquellas propiedades de los cuerpos geométricos que permanecen inalteradas por transformaciones continuas.[1] Es una disciplina que estudia las propiedades de los espacios topológicos y las funciones continuas. La topología se interesa por conceptos como proximidad, número de agujeros, el tipo de consistencia (o textura) que presenta un objeto, comparar objetos y clasificar múltiples atributos donde destacan conectividad, compacidad, metricidad o metrizabilidad, entre otros.
Los matemáticos usan la palabra topología con dos sentidos: informalmente es el sentido arriba especificado, y de manera formal es la referencia a una cierta familia de subconjuntos de un conjunto dado, familia que cumple unas reglas sobre la unión y la intersección —este segundo sentido puede verse desarrollado en el artículo espacio topológico—.
Idea intuitiva[editar]
Coloquialmente, se presenta a la topología como la «geometría de la página de goma (chicle)». Esto hace referencia a que, en la geometría euclídea, dos objetos serán equivalentes mientras podamos transformar uno en otro mediante isometrías (rotaciones, traslaciones, reflexiones, etc.), es decir, mediante transformaciones que conservan las medidas de ángulo, área, longitud, volumen y otras.
En topología, dos objetos son equivalentes en un sentido mucho más amplio. Han de tener el mismo número de trozos, huecos, intersecciones, etc. En topología está permitido doblar, estirar, encoger, retorcer, etc., los objetos, pero siempre que se haga sin romper ni separar lo que estaba unido, ni pegar lo que estaba separado. Por ejemplo, un triángulo es topológicamente lo mismo que una circunferencia, ya que podemos transformar uno en otra de forma continua, sin romper ni pegar. Pero una circunferencia no es lo mismo que un segmento, ya que habría que partirla (o pegarla) por algún punto.
Esta es la razón de que se la llame la «geometría de la página de goma», porque es como si estuviéramos estudiando geometría sobre un papel de goma que pudiera contraerse, estirarse, etc.

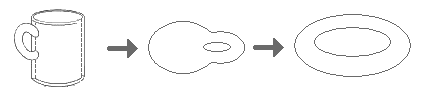
Un chiste habitual entre los topólogos (los matemáticos que se dedican a la topología) es que «un topólogo es una persona incapaz de distinguir una taza de una rosquilla». Pero esta visión, aunque muy intuitiva e ingeniosa, es sesgada y parcial. Por un lado, puede llevar a pensar que la topología trata solo de objetos y conceptos geométricos, siendo más bien al contrario, es la geometría la que trata con un cierto tipo de objetos topológicos. Por otro lado, en muchos casos es imposible dar una imagen o interpretación intuitiva de problemas topológicos o incluso de algunos conceptos. Es frecuente entre los estudiantes primerizos escuchar que «no entienden la topología» y que no les gusta esa rama; generalmente se debe a que se mantienen en esta actitud gráfica. Por último, la topología se nutre también en buena medida de conceptos cuya inspiración se encuentra en el análisis matemático. Se puede decir que casi la totalidad de los conceptos e ideas de esta rama son conceptos e ideas topológicas.
Un ejemplo clarificador[editar]
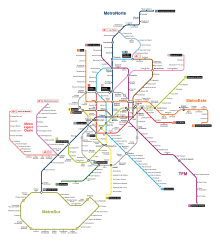
Observemos un plano del metro de Madrid. En él están representadas las estaciones y las líneas de metro que las unen, pero no es geométricamente exacto. La curvatura de las líneas de metro no coincide, ni su longitud a escala, ni la posición relativa de las estaciones... Pero aun así es un plano perfectamente útil. Sin embargo, este plano es exacto en cierto sentido, pues representa fielmente cierto tipo de información, la única que necesitamos para decidir nuestro camino por la red de metro: información topológica.
Historia de la topología[editar]
Históricamente, las primeras ideas topológicas conciernen al concepto de límite y al de completitud de un espacio métrico, y se manifestaron principalmente en la crisis de los inconmesurables de los pitagóricos, ante la aparición de números reales no racionales. El primer acercamiento concreto al concepto de límite y también al de integral aparece en el método de exhaución de Arquímedes. La aparición del análisis matemático en el siglo XVII puso en evidencia la necesidad de formalizar los conceptos de proximidad y continuidad, y la incapacidad de la geometría para tratar este tema. Fue precisamente la fundamentación del cálculo infinitesimal, así como los intentos de formalizar el concepto de variedad en Geometría los que impulsaron la aparición de la topología a finales del siglo XIX y principios del siglo XX.
Se suele fechar el origen de la topología con la resolución por parte de Euler del problema de los puentes de Königsberg, en 1735. Ciertamente, la resolución de Euler del problema utiliza una forma de pensar totalmente topológica, y la solución del problema nos lleva a la característica de Euler, el primer invariante de la topología algebraica, pero sería muy arriesgado y arbitrario fechar en ese momento la aparición de la topología. La situación es exactamente análoga a la del cálculo del área de la elipse por Arquímedes.
El término topología fue usado por primera vez por Johann Benedict Listing en 1836 en una carta a su antiguo profesor de la escuela primaria, Müller, y posteriormente en su libro Vorstudien zur Topologie ('Estudios previos a la topología'), publicado en 1847. Anteriormente se la denominaba analysis situs. Maurice Fréchet introdujo el concepto de espacio métrico en 1906.
| Año | Acontecimiento |
|---|---|
| 300 a. C. | Euclides define las secciones cónicas y estudia los poliedros regulares, una de las formas más básicas estudiadas por los topólogos. |
| 250 a. C. | Arquímedes investiga las curvas espirales y los poliedros truncados. |
| 1735 d. C. | Leonhard Euler resuelve el problema de los puentes de Königsberg. |
| 1858 | Los alemanes August Möbius y Johann Benedict Listing descubren en forma independiente la hoy llamada banda de Möbius. |
| 1890 | Giuseppe Peano aplicando la definición de Jordán demuestra que un cuadrado relleno también es una curva. |
| Década de 1920 | Pável Urysón y Karl Menger definen el concepto de curva a partir de la topología. |
Desarrollo formal[editar]
En el artículo Glosario de topología se encuentra una colección de términos topológicos con su significado. Aquí y ahora nos limitaremos a dar algunas nociones básicas.
Como hemos dicho, el concepto fundamental de la topología es la "relación de proximidad", que puede parecer ambigua y subjetiva. El gran logro de la topología es dar una formulación precisa, objetiva y útil de este concepto. Para ello tomamos un conjunto de referencia , que será el ambiente en el que nos moveremos, y al que llamaremos espacio. Tomaremos un elemento cualquiera de . A los elementos del espacio se les llama puntos, así que será llamado punto, independientemente de que sea una función, un vector, un conjunto, un ideal maximal en un anillo conmutativo y unitario. Un subconjunto de será un entorno de si incluye un conjunto abierto de manera que es elemento de . ¿Qué entenderemos por conjunto abierto? Aquí está el quid de la cuestión: una colección de subconjuntos de se dirá que es una topología sobre si es uno de los elementos de esa colección, si es un elemento de la colección, si la unión de elementos de la colección da como resultado un elemento de la colección y si la intersección finita de elementos de la colección también es un elemento de la colección. A los elementos de la colección se les denomina abiertos de la topología , y al par se le denomina espacio topológico.
Por tanto, las condiciones para que sea topología sobre son las siguientes:
Puede parecer extraño que de una definición tan altamente formal y conjuntista se obtenga una formulación precisa del concepto de proximidad. Lo primero que se observa es que sobre un mismo espacio se pueden definir distintas topologías, generando entonces distintos espacios topológicos. Por otra parte, precisamente la manera en que quede determinada una topología sobre un conjunto (es decir, la elección del criterio que nos permita decidir si un conjunto dado es o no abierto) es lo que va a dar carácter "visualizable" o no a ese espacio topológico.
Una de las maneras más sencillas de determinar una topología es mediante una distancia o métrica, método que solo es aplicable en algunos casos (si bien es cierto que muchos de los casos más intersantes de topologías en la Geometría y del Análisis Matemático pueden determinarse mediante alguna distancia). Una distancia sobre un conjunto es una aplicación que verifica las siguientes propiedades:
- ;
- si y solo si ;
cualesquiera que sean .
Si tenemos definida una distancia sobre , diremos que la pareja
es un espacio métrico. Dado un espacio métrico , queda determinada una topología sobre en la que los conjuntos abiertos son los subconjuntos de tales que cualquiera que sea el punto de existe un número de tal manera que el conjunto está totalmente incluido en . Al conjunto se le denomina bola abierta de centro y radio , y será precisamente un entorno del punto .
Como se ha apuntado antes, por desgracia no toda topología proviene de una distancia, es decir, existen espacios topológicos que no son espacios métricos. Cuando un espacio topológico es además espacio métrico (esto es, cuando dada una topología sobre un conjunto, puede definirse en ese conjunto una distancia de manera que la topología generada por la distancia coincida con la topología dada) se dice que el espacio topológico es metrizable. Un problema clásico en topología es el de determinar qué condiciones debe satisfacer un espacio topológico para que sea metrizable.
Ramas de la topología[editar]
Se suelen considerar principalmente tres ramas:
- la topología general o conjuntista,
- la topología algebraica y
- la topología diferencial.
Además de estas tres ramas, que podríamos decir propiamente topológicas, la implicación en mayor o menor medida en otras disciplinas matemáticas hacen que muchos consideren parte de la topología al análisis funcional, la teoría de la medida, la teoría de nudos (parte de la topología de dimensiones baja), la teoría de grupos topológicos, etc. Es fundamental su contribución a la teoría de grafos, análisis matemático, ecuaciones diferenciales, ecuaciones funcionales, variable compleja, geometría diferencial, geometría algebraica, álgebra conmutativa, estadística, teoría del caos, geometría fractal... Incluso tiene aplicaciones directas en biología, sociología, etc.
Topología general o conjuntista[editar]
Constituye la base de los estudios en topología. En ella se desarrollan tópicos como lo que es un espacio topológico o los entornos de un punto.
Conceptos fundamentales referidos a la topología de un conjunto[editar]
Topología, espacio topológico, abiertos, cerrados, subespacios[editar]
Sea un conjunto cualquiera y el conjunto de sus partes. Una topología sobre es un conjunto que cumpla que , , si entonces , y que si entonces . A los elementos de se les denomina conjuntos abiertos. Al par se le denomina espacio topológico. A los elementos de se les suele denominar puntos.
Nótese que desde un primer momento hemos especificado que el conjunto es cualquiera, no necesariamente un conjunto de naturaleza geométrica. La denominación de espacio (topológico) y de punto se mantiene aun cuando sea un conjunto de números, de funciones, de ecuaciones diferenciales, de figuras geométricas, de vectores, de conjuntos...
Como puede observarse, la definición es muy formal y general, y lo primero que se observa es que sobre un mismo conjunto pueden darse multitud de topologías distintas. Así es. Pero de momento, los conceptos de conjunto abierto en o en o cumplen las condiciones exigibles a una topología. Es precisamente el comprobar que otras familias de conjuntos en otros conjuntos de naturaleza no geométrica que comparten estas mismas propiedades (como en el conjunto de soluciones de una ecuación diferencial, o el conjunto de los ceros de los polinomios con coeficientes en los ideales en un anillo conmutativo, por ejemplo) lo que motiva esta definición. Así podremos aplicar a estos conjuntos las mismas (o parecidas) técnicas topológicas que aplicamos a los abiertos del plano, por ejemplo. La situación es análoga a la que se da en Álgebra Lineal cuando se pasa de trabajar en o a trabajar en espacios vectoriales arbitrarios.
En lo que sigue, representará siempre un espacio topológico.
Ligado al concepto de conjunto abierto está el de conjunto cerrado. Un conjunto se dice que es cerrado si su complementario es un conjunto abierto. Es importante observar que un conjunto que no es abierto no necesariamente ha de ser cerrado, y un conjunto que no sea cerrado no necesariamente ha de ser abierto. Así, existen conjuntos que son abiertos y cerrados a la vez, como , y pueden existir conjuntos que no sean ni abiertos ni cerrados.
Es inmediato comprobar que la intersección de cerrados es un conjunto cerrado, que la unión de una cantidad finita de conjuntos cerrados es un conjunto cerrado, y que tanto como son conjuntos cerrados.
Si , el conjunto es una topología para . Se dirá entonces que el espacio es subespacio topológico del .
La noción de subespacio topológico se presenta de manera natural, y es el concepto análogo al de subgrupo en Teoría de Grupos o al de subespacio vectorial en Álgebra Lineal.
Una propiedad relativa a espacios topológicos se dice que es hereditaria cuando si un espacio la tiene, entonces también la tiene cualquiera de sus subespacios.
Base de una topología, entornos, bases locales, axiomas de numerabilidad[editar]
Una familia se dice que es base (de la topología ) si para cualquiera que sea el existe un conjunto de manera que .
No siempre es cómodo trabajar con una topología. A veces resulta más complicado establecer una topología que una base de topología (como en espacios métricos). En cualquier caso, una base es una manera muy cómoda de establecer una topología. Aún más sencillo es establecer una subbase, que es una familia de conjuntos para la que el conjunto de sus intersecciones finitas forma una base de topología. Uno de los casos más importantes de topología, la de los espacios métricos, viene dado por una base, la del conjunto de bolas abiertas del espacio.
Un espacio topológico se dice que cumple el Segundo Axioma de Numerabilidad (IIAN) si existe alguna base de su topología que tenga cardinalidad numerable.
Sea un conjunto cualquiera y sea un punto arbitrario. Se dice que es entorno de si existe un conjunto abierto de manera que . Todo conjunto abierto es entorno de todos sus puntos. Al conjunto de todos los entornos de un punto se le denomina sistema de entornos de .
Obsérvese que no se ha exigido que un entorno sea un conjunto abierto. Los entornos abiertos son un tipo de entornos muy útiles (sobre todo en Geometría y Análisis) y muy usados, tanto que en muchas ocasiones se omite el calificativo abierto. Esto es un abuso de lenguaje y debe evitarse.
Una colección de entornos de un mismo punto x se dice que es una base de entornos (o base local) de si dado cualquier entorno de existe un de manera que .
Se dice que un espacio topológico cumple el Primer Axioma de Numerabilidad (IAN) si cada punto del espacio tiene alguna base local de cardinal numerable.
Subconjuntos notables asociados a un conjunto[editar]
Ahora podemos establecer una serie de definiciones de gran importancia, pues serán las piezas básicas del estudio de la topología y constituirán la materia prima de los conceptos posteriores.
Interior, exterior, frontera[editar]
Un punto se dirá que es un punto interior de si existe un entorno de tal que . Así, el conjunto de los puntos interiores a es un conjunto abierto, denominado Interior de A, denotado por Int (A) o también como . Es el mayor conjunto abierto incluido en A.
Un punto se dirá que es un punto exterior a si existe un entorno de tal que ⊂ .[3] Asimismo, el conjunto de los puntos exteriores a es otro conjunto abierto, denominado Exterior de A y denotado por Ext (A).
Un punto se dice que es un punto frontera de si todo entorno de es tal que y . Al conjunto de los punto frontera de se le denomina Frontera de A y se denota por Fr(A). En otras palabras, todo entorno con centro en tendrá elementos pertenecientes al conjunto y otros elementos fuera del conjunto . La frontera de es un conjunto cerrado.
Adherencia, acumulación, puntos aislados[editar]
Un punto se dice que es un punto de adherencia de si todo entorno de es tal que . Se hace pues evidente que todo punto interior y todo punto frontera es punto de adherencia. Al conjunto de los puntos de adherencia del conjunto se le denomina adherencia o clausura de , y se denota por o por . La clausura de un conjunto es un conjunto cerrado, y es el menor conjunto cerrado que contiene al conjunto.
Un punto se dice que es un punto de acumulación de si todo entorno de es tal que . Al conjunto de los puntos de acumulación de un conjunto se le denomina acumulación del conjunto, o conjunto derivado, y se le denota por o por .
Un punto se dice que es un punto de -acumulación de si todo entorno de es tal que es un conjunto infinito. Al conjunto de los puntos de -acumulación de un conjunto se le denomina -acumulación del conjunto, o conjunto -derivado, y se le denota por o por . Todo punto de -acumulación es punto de acumulación, y todo punto de acumulación es punto de adherencia del mismo conjunto.
Un punto se dice que es un punto aislado de si existe algún entorno perforado de (es decir, un conjunto de manera que es un entorno de ) de manera que . Al conjunto de los puntos aislados de se le denomina conjunto de los puntos aislados de , y se le denota por . Todo punto aislado es punto frontera y también es punto de adherencia del mismo conjunto.
En topología son de una importancia capital los conjuntos interior y clausura de un conjunto. Su importancia radica en ser, respectivamente, el mayor abierto contenido en el conjunto y el menor cerrado que contiene al conjunto. El interior puede obtenerse también como la unión de todos los abiertos contenidos en el conjunto, y la clausura como la intersección de todos los cerrados que contienen al conjunto. Sin tanta importancia en topología pero de mucha en otras áreas de la Matemática son los conjuntos de acumulación, frontera y de los puntos aislados de un conjunto.
Conceptos fundamentales referidos a aplicaciones continuas y convergencia[editar]
Convergencia[editar]
La idea de la convergencia es la de "aproximar" un objeto por otro, es decir, sustituir un objeto por otro que está próximo a él. Evidentemente, al hacerlo así se está cometiendo un error, error que en general dependerá de lo próximo que se encuentre el objeto sustituido del objeto sustituto. Para hacer esta sustitución de una manera sistemática, de forma que el error pueda ser elegido arbitrariamente pequeño, aparecen distintos tipos de conjuntos. Se obtiene así un proceso de sucesivas aproximaciones que, si todo va bien, terminarían llevándonos al objeto, aunque fuese después de un número infinito de aproximaciones. El más sencillo de estos conjuntos es una sucesión, es decir, una colección infinita (numerable) y ordenada de objetos, aunque con el mismo carácter de orden hay otros conjuntos que reflejan mejor el concepto de convergencia.
Es importante observar que la topología no trabaja con errores ni con aproximaciones. Eso entra en el ámbito del Análisis Numérico e incluso del Análisis Matemático. La topología lo que hace en este problema es aportar las herramientas básicas y los conceptos teóricos para afrontar correctamente el problema, siempre desde un punto de vista conceptual y cualitativo. Estudia qué es lo que debe entenderse cuando se dice que un conjunto (como puede ser una sucesión) se acerca a un objeto (que puede ser un punto, un conjunto, etcétera).
Convergencia de sucesiones[editar]
Una sucesión es una aplicación en un conjunto cuyo dominio es el conjunto de los números naturales. En particular, una sucesión en un espacio topológico es una aplicación .
Una sucesión es el caso más sencillo de aplicación de dominio infinito.
Se dice que es un punto límite de la sucesión , o bien que converge al punto , si se cumple que, cualquiera que sea el entorno de existe un número natural de tal manera que si es otro número natural mayor o igual que (o sea, ) entonces se cumple que .
Hay que hacer dos observaciones sobre esto:
- En primer lugar, puede darse el caso de que la sucesión no tenga puntos límites, o incluso que tenga más de un punto límite. Al conjunto de puntos límites de una sucesión se le denomina límite de (y se le denota por , o también por ).
- En segundo lugar, la interpretación de este concepto es la siguiente: tan cerca como queramos de un punto límite podemos encontrar a todos los puntos de la sucesión, excepto a lo más a una cantidad finita de ellos (que podrá o no ser muy grande, pero no deja de ser finita).
Un punto es punto de aglomeración de la sucesión si cualquiera que sea el entorno de se cumple que el conjunto es infinito. Todo punto límite es punto de aglomeración, pero el recíproco no es cierto. Por ejemplo, los límites de oscilación de una sucesión no convergente de números reales (como por ejemplo la sucesión ) son puntos de aglomeración, pero no son puntos límites (no existe límite para dicha sucesión, mientras que 1 y -1 son puntos de acumulación).
Continuidad de aplicaciones[editar]
Otro concepto totalmente fundamental estudiado en esta rama es el de aplicación continua. Una aplicación entre dos espacios topológicos se dice que es continua si dado cualquier conjunto abierto en , el conjunto es un conjunto abierto en .
Con la misma notación, si , diremos que es continua en cuando se obtiene que es un entorno de , cualquiera que sea el entorno de .
Es inmediato entonces comprobar que es continua cuando y solo cuando es continua en , cualquiera que sea este, es decir, cuando y solo cuando sea continua en cada uno de los puntos de su dominio.
Informalmente hablando, una aplicación es continua si transforma puntos que están cerca en puntos que están cerca, es decir, si respeta la "relación de cercanía". Esto además quiere decir que una función continua no "rompe" los que está unido y no "pega" lo que está separado.
Conjuntos conexos, conexos por caminos y arco-conexos[editar]
Un conjunto se dice que es conexo si no puede expresarse como unión de dos abiertos disjuntos no vacíos.
Un conjunto se dice que es conexo por caminos si todo par de puntos puede unirse mediante un camino, esto es, continua de tal manera que y . Todo conjunto conexo por caminos es conexo, pero no todo conjunto conexo es conexo por caminos (ver, por ejemplo, el seno del topólogo).
Estos conjuntos están "hechos de una pieza" (los conexos) o "hechos de manera que no tienen piezas totalmente sueltas" (los conexos por caminos). Naturalmente esto es solo una manera de interpretarlos. Las piezas de un conjunto (los mayores subconjuntos conexos que contiene el conjunto) se denominan "componentes conexas". Por ejemplo, un puñado de arena sería un conjunto en el que las componentes conexas son cada granito de arena. Un espejo roto sería un conjunto en el que cada trozo de espejo es una componente conexa. Una bola de hierro es un conjunto con una sola componente conexa, es decir, un conjunto conexo. Una rejilla también es un conjunto conexo, formado por una sola componente conexa.
Existe otra noción de conexión, la conexión por arcos o arco conexión ligeramente más restrictiva que la conexión por caminos. Se exige que el camino sea un homeomorfismo sobre su imagen. Aun así, la conexión por arcos y por caminos coinciden sobre los espacios de Hausdorff.
Compacidad[editar]
Los conjuntos compactos son un tipo de conjunto mucho más difíciles de definir. Un espacio es compacto si para todo recubrimiento por abiertos (familia de abiertos cuya unión contiene al espacio total X) existe subrecubrimiento finito (familia finita de abiertos, formada solo por conjuntos de la familia anterior, cuya unión contiene a X).
En un espacio métrico, un conjunto compacto cumple dos condiciones: es "cerrado", es decir contiene a todos sus puntos frontera; y es "acotado", es decir es posible trazar una bola que lo contenga, aunque la recíproca no es necesariamente cierta. Es decir, pueden existir conjuntos cerrados y acotados que no sean compactos. La compacidad es una propiedad muy importante en topología, así como en Geometría y en Análisis Matemático.
En cualquier espacio topológico, un conjunto cerrado dentro de un compacto, siempre es compacto. Además, en un espacio topológico de Hausdorff, un compacto siempre es cerrado.
Metrización[editar]
Una topología sobre un conjunto es metrizable si es posible encontrar una distancia de forma que los abiertos para esa distancia sean exactamente los abiertos de la topología de partida. La metrizabilidad es también una propiedad muy deseable en un espacio topológico, pues nos permite dar una caracterización muy sencilla de los abiertos de la topología, además de implicar otras ciertas propiedades.
Separación[editar]
Las propiedades de separación son ciertas propiedades, cada una un grado más restrictiva que la anterior, que nos indican la "resolución" o "finura del grano" de una topología. Por ejemplo, la propiedad de separación T2 significa que para dos puntos distintos siempre pueden encontrarse entornos disjuntos (es decir que no se cortan).
Densidad[editar]
Un conjunto es denso en el espacio si está "cerca de todos los puntos" de ese espacio. De manera más precisa, un conjunto es denso si su clausura topológica es todo el espacio. Equivalentemente, un conjunto es denso si su intersección con cualquier abierto no vacío del espacio es también no vacía. Un conjunto se dice que es separable si tiene algún subconjunto denso y numerable.
Topología producto y topología cociente[editar]
La topología producto nos proporciona una manera de dotar de una topología al producto cartesiano de varios espacios topológicos, de tal manera que se conserven buenas propiedades, en particular que las proyecciones sobre cada factor sean aplicaciones continuas y abiertas. La topología cociente nos proporciona una manera de dotar de una topología al cociente (espacio de clases) de un espacio por una relación de equivalencia, de manera que tenga el mayor número posible de conjuntos abiertos y sin embargo la proyección sea continua (es decir la imagen recíproca de cada abierto sea un abierto).
Topología algebraica[editar]
La topología algebraica estudia ciertas propiedades relacionadas con la conexión de un espacio, propiedades que podríamos describir como la "porosidad" de un espacio, la cantidad de boquetes que presenta. Para ello se vale de instrumentos algebraicos, fundamentalmente la teoría de grupos y el álgebra homológica, hasta tal punto que su desarrollo es totalmente algebraico.
En la topología algebraica se consideran una gran diversidad de problemas incluidos en la teoría de nudos por ejemplo, o en la teoría de homotopías y la teoría de homología.
Para comprender sucintamente estas cuestiones, volvamos a los ejemplos de conjuntos conexos. Según hemos dicho, una rejilla, una bola de hierro o una esponja son conjuntos conexos. Sin embargo todos entendemos que parece que no tienen el mismo «grados de conexión», por expresarlo de alguna manera. Mientras que una bola de hierro es maciza, una esponja y una rejilla tienen agujeros, e incluso parece claro que entre estos hay también una cierta diferencia. La homotopía y la homología tratan estas cuestiones.
Véase también[editar]
 Portal:Matemática. Contenido relacionado con Matemática.
Portal:Matemática. Contenido relacionado con Matemática.- Agujero de gusano
- Espacio topológico
- Banda de Möbius
- Botella de Klein
- Nudo borromeo
- Problema de los puentes de Königsberg
- Topología cociente
- Topología cuántica
- Topología geoespacial
- Topología geométrica
- Glosario de topología
- Origami
Referencias[editar]
- ↑ Stewart, Ian: Conceptos de matemática moderna. Alianza Universidad, 1988. p. 171.
- ↑ Tony Crilly (2011). 50 cosas que hay que saber sobre matemáticas. Ed. Ariel. ISBN 978-987-1496-09-9.
- ↑ Ayala y otros: "Elementos de la topología general" ISBN 84-7829-006-0
Enlaces externos[editar]
 Wikimedia Commons alberga una galería multimedia sobre Topología.
Wikimedia Commons alberga una galería multimedia sobre Topología. Wikcionario tiene definiciones y otra información sobre topología.
Wikcionario tiene definiciones y otra información sobre topología. Wikiquote alberga frases célebres de o sobre los Topólogos.
Wikiquote alberga frases célebres de o sobre los Topólogos. Wikilibros alberga un libro o manual sobre Espacios Métricos.
Wikilibros alberga un libro o manual sobre Espacios Métricos. Wikiversidad alberga proyectos de aprendizaje sobre Topología.
Wikiversidad alberga proyectos de aprendizaje sobre Topología.- http://www.ehu.es/~mtwmastm/sigma20.pdf Marta Macho Stadler: ¿Qué es la topología?
- https://web.archive.org/web/20090419031102/http://rinconmatematico.com/chamizo/APtopo.pdf La Topología... no es tan difícil.
- http://topologia.wordpress.com Juegos topológicos.
- http://www.elcorreoelectronico.com/esquemas-topologia/topologia La Topología en el correo electrónico.

































































































![{\displaystyle \,\forall x,y\in X\quad \exists \phi :[0,1]\longrightarrow X}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2b1538c7f8cc5a20d47a5ca3f9c206f28da99db)

