Topología cociente

Ilustración de un espacio cociente, S², obtenida por pegado del contorno (en azul) del disco D² a un solo punto.

En matemáticas, la topología cociente consiste intuitivamente en crear una topología pegando ciertos puntos sobre otros, en un espacio dado, por medio de una relación de equivalencia bien definida. El nuevo espacio así generado recibe el nombre de espacio cociente. Ejemplos conocidos son el toro matemático o la banda de Möbius.

Definición

Sean $(X,{\mathcal {T}}_{X})\$ un espacio topológico y $\sim \,$ una relación de equivalencia sobre $X\$. El conjunto cociente $Y=X/{\sim }\,$ es el conjunto de clases de equivalencia de los elementos de $X\$:

$Y=\{[x]:x\in X\}.$

Los conjuntos abiertos que conforman la llamada topología cociente sobre $Y$ son los conjuntos de las clases de equivalencia cuyas uniones son conjuntos abiertos en $X$:

${\mathcal {T}}_{\sim }=\{U\subseteq Y:\bigcup _{[x]\in U}[x]\in {\mathcal {T}}_{X}\}.$

Definición equivalente: sea la aplicación proyección $p:X\rightarrow X/{\sim }$ dada por $p(x)=[x]$, se definen los abiertos de ${\mathcal {T}}_{\sim }$ como los conjuntos $U\subseteq X/{\sim }$ tales que $p^{-1}(U)\subseteq X$ es abierto. Es decir, un conjunto de clases de equivalencia es abierto si los elementos que las forman son un conjunto abierto de la topología original.

${\mathcal {T}}_{\sim }$ es, en efecto, una topología. (Según la definición equivalente)

$(1)$ $\emptyset \in {\mathcal {T}}_{\sim }$ ya que $p^{-1}(\emptyset )=\emptyset$, que es un abierto de ${\mathcal {T}}_{X}$ por definición de topología. $(2)$ $X/{\sim }\in {\mathcal {T}}_{\sim }$ ya que $p^{-1}(X/{\sim })=X$, que es un abierto de ${\mathcal {T}}_{X}$ por definición de topología. $(3)$ Dados $\{U_{i}\}_{i\in I}$ abiertos de $X/{\sim }$, tenemos que $p^{-1}(U_{i})\in {\mathcal {T}}_{X}\quad \forall i\in I$ por definición de topología cociente. Por ser ${\mathcal {T}}_{X}$ topología, $\bigcup _{i\in I}{p^{-1}(U_{i})}\in {\mathcal {T}}_{X}$, pero $\bigcup _{i\in I}{p^{-1}(U_{i})}=p^{-1}\left(\bigcup _{i\in I}{U_{i}}\right)\Rightarrow \bigcup _{i\in I}{U_{i}}\in {\mathcal {T}}_{\sim }$. $(4)$ Dados $\{U_{i}\}_{i=1}^{n}$ abiertos de $X/{\sim }$, tenemos que $p^{-1}(U_{i})\in {\mathcal {T}}_{X}\quad \forall i=1,\dots ,n$ por definición de topología cociente. Por ser ${\mathcal {T}}_{X}$ topología, $\bigcap _{i=1}^{n}{p^{-1}(U_{i})}\in {\mathcal {T}}_{X}$, pero $\bigcap _{i=1}^{n}{p^{-1}(U_{i})}=p^{-1}\left(\bigcap _{i=1}^{n}{U_{i}}\right)\Rightarrow \bigcap _{i=1}^{n}{U_{i}}\in {\mathcal {T}}_{\sim }$.

Propiedades

• La aplicación proyección al cociente $p:X\rightarrow X/{\sim }$ que envía a cada elemento a su clase de equivalencia correspondiente es continua​y la topología cociente es la más fina que se puede definir en $X/{\sim }$ que cumple esto. Es decir, la topología cociente es la topología final respecto a la proyección al cociente.

Demostración

Claramente, la topología cociente hace la proyección al cociente continua. En efecto, para ver que es continua, tomamos $U\subseteq X/{\sim }$ abierto y vemos que su antiimagen por $p$ es abierta de $X$. Pero por ser $U$ abierto de la topología cociente, por definición, $p^{-1}(U)\subseteq X$ es un abierto, que es lo que queríamos. Que es la más fina que lo cumple también es inmediato por definición. Si ${\mathcal {T}}$ es una topología de $X/{\sim }$ más fina que ${\mathcal {T}}_{\sim }$, por definición, necesariamente tiene un abierto $U\subseteq X/{\sim }$ con $p^{-1}(U)$ no abierto de $X$, y esto contradice la definición de continuidad.

• Sean $p\colon X\to X/{\sim }$ la proyección al cociente y $f\colon X/{\sim }\to Y$ una aplicación. Entonces, la aplicación $f$ es continua si, y sólo si, la composición $f\circ p\colon X{\overset {p}{\to }}X/{\sim }{\overset {f}{\to }}Y$ es continua.​

Demostración

$(\Rightarrow )$ Como $f$ es continua por hipótesis y ya se ha demostrado que $p$ es continua, $f\circ p$ es continua por ser composición de aplicaciones continuas. $(\Leftarrow )$ Sea $U\subseteq Y$ abierto y veamos que su antiimagen por $f$, $f^{-1}(U)$, es un abierto de $X/{\sim }$. Esto es equivalente, por definición de topología cociente, a ver que $p^{-1}(f^{-1}(U))=(f\circ p)^{-1}(U)$ es un abierto de $X$, pero esto es cierto por ser $f\circ p$ continua, por hipótesis. $\quad \square$

• La propiedad universal: La topología cociente es la única topología que cumple que para cualquier espacio topológico (Z, T) y cualquier función g:(Y, $T_{f}$) $\rightarrow$ (Z, T) se tiene que g es continua si y sólo si $g\circ f$ es continua

Ejemplos

En los siguientes ejemplos los homeomorfismos se construyen primero deformando el espacio cociente sin tener en cuenta la relación de equivalencia (cortándola) y después pegando los trozos que estaban relacionados. Es decir, estamos admitiendo que podemos construir un espacio entre dos espacios cociente a partir de uno entre los espacios originales siempre y cuando los elementos relacionados antes y después del homeomorfismo sean los mismos. Este resultado, que justifica que las construcciones siguientes son correctas, se conoce como lema de cortar y pegar, y se demuestra a continuación

Lema de cortar y pegar: Sea $f\colon X\to Y$ un homeomorfismo y $\sim _{X},\sim _{Y}$ relaciones de equivalencia en $X$ e $Y$, respectivamente, que satisfacen que $x\sim _{X}x'\Leftrightarrow f(x)\sim _{Y}f(x')\quad \forall x,x'\in X$. Entonces, la aplicación $f_{\sim }\colon X/{\sim _{X}}\to Y/{\sim _{Y}}$ dada por $[x]_{X}\mapsto f_{\sim }([x]_{X})=[f(x)]_{Y}$ está bien definida y es un homeomorfismo.

$(1)$ Está bien definida: sean $x\sim _{X}x'$ y veamos que la imagen por $f_{\sim }$ de su clase de equivalencia $[x]_{X}$ no depende de cuál tomemos como representante. En efecto, $x\sim _{X}x'{\overset {\text{Hipótesis}}{\Rightarrow }}f(x)\sim _{Y}f(x')\Rightarrow [f(x)]_{Y}=[f(x')]_{Y}$, que es lo que queríamos. $(2)$ $f$ es exhaustiva: Sea $[y]_{Y}\in Y/{\sim _{Y}}$, con representante $y$. Como $f$ es homeomorfismo y, en particular, exhaustiva, $\exists x\in X$ tal que $f(x)=y$. Pero entonces $[y]_{Y}=[f(x)]_{Y}=f_{\sim }([x]_{X})$ y tenemos una antiimagen $[x]_{X}$ de $[y]_{Y}$. $(3)$ $f$ es inyectiva: Supongamos que $f_{\sim }([x]_{X})=f_{\sim }([x']_{X})$ y veamos que $[x]_{X}=[x']_{X}$. En efecto, $f_{\sim }([x]_{X})=f_{\sim }([x']_{X})\Rightarrow [f(x)]_{Y}=[f(x')]_{Y}\Rightarrow f(x)\sim _{Y}f(x'){\overset {\text{Hipótesis}}{\Rightarrow }}x\sim _{X}x'\Rightarrow [x]_{X}=[x']_{X}$. $(4)$ $f$ es continua. Sean $\pi _{X},\pi _{Y}$ las proyecciones a $X/{\sim _{X}},Y/{\sim _{Y}}$, respectivamente. Tenemos que $\pi _{Y}\circ f=f_{\sim }\circ \pi _{X}$: En efecto, dado $x\in X$, $\pi _{Y}(f(x))=[f(x)]_{Y}{\overset {\text{def}}{=}}f_{\sim }([x]_{X})=f_{\sim }(\pi _{X}(x))$. Pero $f$ es continua por ser homeomorfismo y $\pi _{Y}$ por ser una proyección al cociente. Por tanto, también lo es la composición $\pi _{Y}\circ f=f_{\sim }\circ \pi _{X}$, pero por la segunda propiedad del apartado de propiedades esto quiere decir que $f_{\sim }$ es continua. $(5)$ $f^{-1}$ es continua. La demostración es la misma que $(4)$ pero heredando continuidad de $f^{-1}$ (continua por ser $f$ homeomorfismo). $\quad \square$

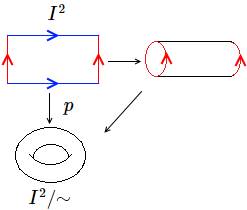
• El toro como conjunto cociente:​ Sobre $I^{2}=[0,1]\times [0,1]$ se define la relación de equivalencia $(x,0)\sim (x,1)$ y $(0,y)\sim (1,y)\quad \forall x,y\in [0,1]$. El espacio cociente $I^{2}/{\sim }$ es homeomorfo a un toro.

Toro

• La banda de Möbius como conjunto cociente:​ Sobre $I^{2}$ se define la relación de equivalencia $(0,y)\sim (1,1-y)\quad \forall y\in [0,1]$. El espacio cociente $I^{2}/{\sim }$ es homeomorfo a una banda de Möbius.

Banda de Möbius

• La botella de Klein como conjunto cociente:​ Sobre $I^{2}$ se define la relación de equivalencia $(x,0)\sim (x,1)$ y $(0,y)\sim (1,1-y)\quad \forall x,y\in [0,1]$. El espacio cociente $I^{2}/{\sim }$ es homeomorfo a una botella de Klein (es difícil de visualizar puesto que no es homeomorfo a un subespacio de $\mathbb {R} ^{3}$).

• 
• 
• 
• 
• 
• 
• 

• La esfera como conjunto cociente:​ Sobre $\{(x,y):|x|+|y|\leq 1\}$ (cuadrado de vértices $(1,0),(0,1),(-1,0),(0,-1)$) se define la relación de equivalencia $(x,y)\sim (-x,y)$ para $(x,y)$ de la frontera. El espacio cociente correspondiente es homeomorfo a una esfera.

Bibliografía

• Robles Corbalá Carlos Alberto, "Topología general" primera edición Universidad de Sonora.
• Weisstein, Eric W. «Espacio cociente». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Quotient space en PlanetMath.
• Hazewinkel, Michiel, ed. (2001), «Quotient_space&oldid=11882», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104 .

Enlaces externos

• López Camino, Rafael. «Capítulo 7. espacios cocientes» (PDF). Universidad de Granada. Archivado desde el original el 14 de agosto de 2011. Consultado el 30 de abril de 2011. 

• Wikilibros alberga un libro o manual sobre Espacios Métricos/Productos y Cocientes. incluyendo un capítulo sobre espacios cocientes.

• Datos: Q77981916