Punto aislado
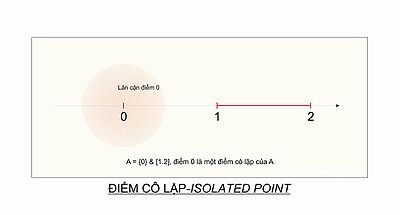
En matemáticas, y más precisamente en topología, un punto x de un espacio topológico E se llama punto aislado, si la intersección de E con un entorno de x consiste en el punto x únicamente.
Definiciones equivalentes:
- es un conjunto abierto ;
- es un entorno de x ;
- x no es adherente a (x no es un punto de acumulación).
En particular, en un espacio euclídeo (o un espacio métrico), x es un punto aislado de E si existe una bola abierta centrada en x que no contiene otros puntos de E.
Un espacio topológico en el cual todo punto es un punto aislado se llama discreto.
Un conjunto cerrado que no posee ningún punto aislado se llama conjunto perfecto.
El número de puntos aislados es un invariante topológico, es decir que si dos espacios topológicos X e Y son homeomorfos, el número de puntos aislados en ambos es igual.
Ejemplos[editar]
- En el espacio topológico con la topología natural, el punto 0 es un punto aislado.
- En el espacio , cada punto de tipo 1/k es un punto aislado, pero el 0 no lo es.
- El conjunto de los números naturales es un conjunto discreto donde cada elemento del conjunto es un punto aislado.
![{\displaystyle \{0\}\cup [1,2]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1523ab6bb767930e43ebaf0a5111f5b86a740f85)
Véase también[editar]
Referencias[editar]
- Hazewinkel, Michiel, ed. (2001), «Isolated_point&oldid=13250», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104.
- Weisstein, Eric W. «IsolatedPoint». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
| Control de autoridades |
|
|---|
Datos: Q1142889