Leonhard Euler
Leonhard Paul Euler (pron. AFI: [ˈɔʏlɐ] en alemán moderno[2][3]) (Basilea, Suiza; 15 de abril de 1707-San Petersburgo, Imperio ruso; 18 de septiembre de 1783), conocido como Leonhard Euler y también llamado Leonardo Euler en español,[4] fue un matemático y físico suizo. Se trata del principal matemático del siglo XVIII y uno de los más grandes y prolíficos de todos los tiempos, muy conocido por el número de Euler (e), número que aparece en muchas fórmulas de cálculo y física.
Vivió en San Petersburgo (Rusia), y también en Berlín (Prusia) la mayor parte de su vida adulta y realizó importantes descubrimientos en áreas tan diversas como el cálculo o la teoría de grafos. También introdujo gran parte de la terminología moderna y notación matemática, particularmente para el área del análisis matemático, como, por ejemplo, la noción de función matemática.[5] Asimismo se le conoce por sus trabajos en los campos de la mecánica, la óptica y la astronomía.
Euler ha sido uno de los matemáticos más grandes, más prolíficos, y se calcula que sus obras completas reunidas podrían ocupar entre 60 y 80 volúmenes.[6] Una afirmación atribuida a Pierre Simon Laplace expresa la influencia de Euler en los matemáticos posteriores: «Lean a Euler, lean a Euler, él es el maestro de todos nosotros».[7]
Biografía[editar]
Primeros años[editar]
Leonhard Euler nació en Basilea (Suiza), hijo de Paul Euler, un pastor calvinista, y de Marguerite Brucker, hija de otro pastor. Tuvo dos hermanas pequeñas, llamadas Anna Maria y Maria Magdalena. Poco después de su nacimiento, su familia se trasladó de Basilea al cercano pueblo de Riehen, en donde Euler pasó su infancia. Por su parte, Paul Euler era amigo de los Bernoulli, famosa familia de matemáticos entre los que destacaba Johann Bernoulli, que en ese momento era ya considerado el principal matemático europeo y que ejercería una gran influencia sobre el joven Leonhard.
La educación formal de Euler comenzó en la ciudad de Basilea, donde le enviaron a vivir con su abuela materna. A la edad de trece años se matriculó en la Universidad de Basilea y en 1723 recibió el título de maestro de Filosofía tras una disertación comparativa de las filosofías de René Descartes e Isaac Newton. Por entonces, Euler tomaba lecciones particulares todos los sábados por la tarde con Johann Bernoulli, quien descubrió rápidamente el increíble talento para las matemáticas de su nuevo pupilo.[8]
En aquella época, Euler se dedicaba a estudiar teología, griego y hebreo, siguiendo los deseos de su padre, y con la vista puesta en llegar a ser también pastor. Johann Bernoulli intervino para convencer a Paul Euler de que Leonhard estaba destinado a ser un gran matemático. En 1726 Euler finalizó su Doctorado con una tesis sobre la propagación del sonido bajo el título De Sono[9] y en 1727 participó en el concurso promovido por la Academia de las Ciencias francesa por el cual se solicitaba a los concursantes que encontraran la mejor forma posible de ubicar el mástil en un buque. Ganó el segundo puesto, detrás de Pierre Bouguer, que es conocido por ser el padre de la arquitectura naval. Más adelante, Euler conseguiría ganar ese premio hasta en doce ocasiones.[10][11]
San Petersburgo[editar]
En aquel tiempo, los dos hijos de Johann Bernoulli, Daniel y Nicolás, se encontraban trabajando en la Academia de las ciencias de Rusia en San Petersburgo. En julio de 1726, Nicolás murió de apendicitis tras haber vivido un año en Rusia y, cuando Daniel asumió el cargo de su hermano en el departamento de Matemáticas y Física, recomendó que el puesto que había dejado vacante en Fisiología fuese ocupado por su amigo Euler. En noviembre de ese mismo año, Euler aceptó la oferta, aunque retrasó su salida hacia San Petersburgo mientras intentaba conseguir, sin éxito, un puesto de profesor de Física en la Universidad de Basilea.[12]

Euler llegó a la capital rusa el 17 de mayo de 1727. Fue ascendido desde su puesto en el departamento médico de la Academia a otro en el departamento de matemáticas, en el que trabajó con Daniel Bernoulli, a menudo en estrecha colaboración. Euler aprendió ruso y se estableció finalmente en San Petersburgo a vivir. Llegó incluso a tomar un trabajo adicional como médico de la Armada de Rusia.[13]
La Academia de San Petersburgo, creada por Pedro I de Rusia, tenía el objetivo de mejorar el nivel educativo en Rusia y de reducir la diferencia científica existente entre ese país y la Europa Occidental. Como resultado, se implementaron una serie de medidas para atraer a eruditos extranjeros como Euler. La Academia poseía amplios recursos financieros y una biblioteca muy extensa, extraída directamente de las bibliotecas privadas de Pedro I y de la nobleza. La Academia admitía a un número muy reducido de estudiantes para facilitar la labor de enseñanza, a la vez que se enfatizaba la labor de investigación y se ofrecía a la facultad tanto el tiempo como la libertad necesarios para resolver cuestiones científicas.[14]
Sin embargo, la principal benefactora de la Academia, la emperatriz Catalina I de Rusia, que había continuado con la política progresista de su marido, murió el mismo día de la llegada de Euler a Rusia. Su muerte incrementó el poder de la nobleza, puesto que el nuevo emperador pasó a ser Pedro II de Rusia, por entonces un niño de tan solo doce años de edad. La nobleza sospechaba de los científicos extranjeros de la Academia, por lo que cortó la cuantía de recursos dedicados a la misma y provocó otra serie de dificultades para Euler y sus coetáneos.
Las condiciones mejoraron ligeramente tras la muerte de Pedro II, y Euler fue poco a poco ascendiendo en la jerarquía de la Academia, convirtiéndose en profesor de Física en 1731. Dos años más tarde, Daniel Bernoulli, harto de las dificultades que le planteaban la censura y la hostilidad a la que se enfrentaban en San Petersburgo, dejó la ciudad y volvió a Basilea. Euler le sucedió como director del departamento de Matemáticas.[15]
El 7 de enero de 1734, Euler contrajo matrimonio con Katharina Gsell (1707-1773) (hija del pintor suizo de la Academia de San Petersburgo Georg Gsell, y cuya madrastra era la pintora Dorothea Maria Graff, hija a su vez de la famosa naturalista holandesa Maria Sibylla Merian). La joven pareja compró una casa al lado del río Nevá y llegó a concebir trece hijos, si bien solo cinco sobrevivieron hasta la edad adulta.[16] El mayor de estos hijos, Johann Euler, fue matemático y astrónomo y miembro de la Academia de Berlín desde 1754.
Berlín[editar]
Preocupado por los acontecimientos políticos que estaban teniendo lugar en Rusia, Euler partió de San Petersburgo el 19 de junio de 1741 para aceptar un cargo en la Academia de Berlín, cargo que le había sido ofrecido por Federico II el Grande, rey de Prusia. Vivió veinticinco años en Berlín, en donde escribió más de 380 artículos. También publicó aquí dos de sus principales obras: la Introductio in analysin infinitorum, un texto sobre las funciones matemáticas publicado en 1748, y la Institutiones calculi differentialis,[17] publicada en 1755 y que versaba sobre el cálculo diferencial.[18]
Además, se le ofreció a Euler un puesto como tutor de la princesa de Anhalt-Dessau, la sobrina de Federico. Euler escribió más de 200 cartas dirigidas a la princesa que más tarde serían recopiladas en un volumen titulado Cartas de Euler sobre distintos temas de Filosofía Natural dirigidas a una Princesa alemana. Este trabajo recopilaba la exposición de Euler sobre varios temas de física y matemáticas, así como una visión de su personalidad y de sus creencias religiosas. El libro se convirtió en el más leído de todas sus obras, siendo publicado a lo largo y ancho del continente europeo y en los Estados Unidos. La popularidad que llegaron a alcanzar estas Cartas sirve de testimonio sobre la habilidad de Euler de comunicar cuestiones científicas a una audiencia menos cualificada.[18]
A pesar de la inmensa contribución de Euler al prestigio de la Academia, fue obligado finalmente a dejar Berlín. El motivo de esto fue, en parte, un conflicto de personalidad entre el matemático y el propio rey Federico, que llegó a ver a Euler como una persona muy poco sofisticada, y especialmente en comparación con el círculo de filósofos que el rey alemán había logrado congregar en la Academia. Voltaire, en particular, era uno de esos filósofos y gozaba de una posición preeminente en el círculo social del rey. Euler, como un simple hombre de carácter religioso y trabajador, era muy convencional en sus creencias y en sus gustos, representando en cierta forma lo contrario que Voltaire. Euler tenía conocimientos limitados de retórica y solía debatir cuestiones sobre las que tenía pocos conocimientos, lo cual le hacía un objetivo frecuente de los ataques del filósofo.[18] Por ejemplo, Euler protagonizó varias discusiones metafísicas con Voltaire, de las que solía retirarse enfurecido por su incapacidad en la retórica y la metafísica. Federico también mostró su descontento con las habilidades prácticas de ingeniería de Euler:
Quería tener una bomba de agua en mi jardín: Euler calculó la fuerza necesaria de las ruedas para elevar el agua a un depósito, desde el que caería después a través de canalizaciones para finalmente manar en el palacio de Sanssouci. Mi molino fue construido de forma geométrica y no podía elevar una bocanada de agua hasta más allá de cinco pasos hacia la reserva. ¡Vanidad de las vanidades! ¡Vanidad de la geometría!
[20]
Deterioro de la visión[editar]

La vista de Euler fue empeorando a lo largo de su vida. En el año 1735 Euler sufrió una fiebre casi fatal, y tres años después de dicho acontecimiento quedó prácticamente ciego del ojo derecho. Euler, sin embargo, prefería acusar de este hecho al trabajo de cartografía que realizaba para la Academia de San Petersburgo.
La vista de ese ojo empeoró a lo largo de su estancia en Alemania, hasta el punto de que Federico II hacía referencia a él como el Cíclope. Euler más tarde sufrió cataratas en su ojo sano, el izquierdo, lo que le dejó prácticamente ciego pocas semanas después de haber sido diagnosticadas. A pesar de ello, era poco probable que sus problemas de visión le afectaran a su productividad intelectual, dado que lo compensó con su gran capacidad de cálculo mental. De manera similar, Euler estudió la Eneida de Virgilio desde el comienzo hasta el final.[6] También podía calcular de manera instantánea preguntas de fórmulas de trigonometría y las primeras 6 potencias de los primeros 100 números primos sin papel ni lápiz.[22]
Pasó los últimos años de su vida ciego, pero siguió trabajando. Muchos trabajos se los dictó a su hijo mayor. Esto incrementó el respeto que la comunidad científica ya tenía por él. El matemático francés François Arago (1786-1853) se refirió en cierta ocasión a él diciendo:
«Euler calculaba sin esfuerzo aparente, como los hombres respiran, o como las águilas se sostienen en el aire».[23]
Retorno a Rusia[editar]

La situación en Rusia había mejorado enormemente tras el ascenso de Catalina la Grande, por lo que en 1766 Euler aceptó una invitación para volver a la Academia de San Petersburgo y pasar allí el resto de su vida. Su segunda época en Rusia, sin embargo, estuvo marcada por la tragedia: un incendio en San Petersburgo en 1771 le costó su casa y casi su vida, y en 1773 perdió a su esposa Katharina Gsell, después de cuarenta años de matrimonio. Euler se volvió a casar tres años más tarde con Salome Abigail Gsell (1723-1794),[24] hermana de padre de su primera mujer. Este segundo matrimonio duró hasta la muerte del matemático.
El 18 de septiembre de 1783, Euler falleció en la ciudad de San Petersburgo tras sufrir un accidente cerebrovascular y fue enterrado junto con su primera esposa en el Cementerio Luterano ubicado en la isla Vasilievski. Sus restos fueron trasladados por los soviéticos al Monasterio de Alejandro Nevski (también conocido como Leningradsky Nikropol).
El matemático y filósofo francés Nicolas de Condorcet escribió su elogio funerario para la Academia francesa:
…il cessa de calculer et de vivre — … dejó de calcular y de vivir.[25]
Por su parte, Nikolaus von Fuss, ahijado de Euler y secretario de la Academia Imperial de San Petersburgo, escribió un relato de su vida junto con un listado de sus obras.
Contribución a las matemáticas y a otras áreas científicas[editar]

Euler trabajó prácticamente en todos los ámbitos de las matemáticas: geometría, cálculo, trigonometría, álgebra, teoría de números, además de física continua, teoría lunar y otras áreas de la física. Adicionalmente, hizo aportes relevantes a la lógica matemática con su diagrama de conjuntos.
Ha sido uno de los matemáticos más prolíficos de la historia. Su actividad de publicación fue incesante (un promedio de 800 páginas de artículos al año en su época de mayor producción, entre 1727 y 1783), y una buena parte de su obra completa está sin publicar. La labor de recopilación y publicación completa de sus trabajos, llamados Opera Omnia,[26] comenzó en 1911 y hasta la fecha ha llegado a publicar 76 volúmenes. El proyecto inicial planeaba el trabajo sobre 887 títulos en 72 volúmenes. Se le considera el ser humano con mayor número de trabajos y artículos en cualquier campo del saber, solo equiparable a Gauss. Si se imprimiesen todos sus trabajos, muchos de los cuales son de una importancia fundamental, ocuparían entre 60 y 80 volúmenes.[6] Además, y según el matemático Hanspeter Kraft, presidente de la Comisión Euler de la Universidad de Basilea, no se ha estudiado más de un 10 % de sus escritos.[27] Por todo ello, el nombre de Euler está asociado a un gran número de cuestiones matemáticas.
Se cree que fue el que dio origen al pasatiempos sudoku creando una serie de pautas para el cálculo de probabilidades.[28]
Notación matemática[editar]
Euler introdujo y popularizó varias convenciones referentes a la notación en los escritos matemáticos en sus numerosos y muy utilizados libros de texto. Posiblemente lo más notable fue la introducción del concepto de función matemática,[5] siendo el primero en escribir f(x) para hacer referencia a la función f aplicada sobre el argumento x. Esta nueva forma de notación ofrecía más comodidad frente a los rudimentarios métodos del cálculo infinitesimal existentes hasta la fecha, iniciados por Newton y Leibniz, pero desarrollados basándose en las matemáticas del último.
También introdujo la notación moderna de las funciones trigonométricas, la letra e como base del logaritmo natural o neperiano (el número e es conocido también como el número de Euler), la letra griega Σ como símbolo de los sumatorios y la letra para hacer referencia a la unidad imaginaria.[29] El uso de la letra griega π para hacer referencia al cociente entre la longitud de la circunferencia y la longitud de su diámetro también fue popularizado por Euler, aunque él no fue el primero en usar ese símbolo.[30]
Análisis[editar]
El desarrollo del cálculo era una de las cuestiones principales de la investigación matemática del siglo XVIII, y la familia Bernoulli había sido responsable de gran parte del progreso realizado hasta entonces. Gracias a su influencia, el estudio del cálculo se convirtió en uno de los principales objetos del trabajo de Euler. Si bien algunas de sus demostraciones matemáticas no son aceptables bajo los estándares modernos de rigor matemático,[31] es cierto que sus ideas supusieron grandes avances en ese campo.
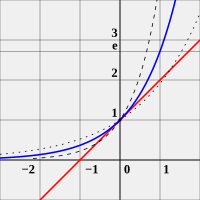
El número e[editar]
Euler definió la constante matemática conocida como número como aquel número complejo tal que el valor de la derivada (la pendiente de la línea tangente) de la función en el punto es exactamente 1. Es más, es el número real tal que la función se tiene como derivada a sí misma. La función es también llamada función exponencial y su función inversa es el logaritmo natural o logaritmo en base e, mal llamado logaritmo neperiano.
El número e puede ser representado como un número real en varias formas: como una serie infinita, un producto infinito, una fracción continua o como el límite de una sucesión. La principal de estas representaciones, particularmente en los cursos básicos de cálculo, tiene como forma el límite:
y también la serie:
.
Además, Euler es muy conocido por su análisis y su frecuente utilización de la serie de potencias, es decir, la expresión de funciones como una suma infinita de términos como la siguiente:
Uno de los famosos logros de Euler fue el descubrimiento de la expansión de series de potencias de la función arcotangente. Su atrevido, aunque, según los estándares modernos, técnicamente incorrecto uso de las series de potencias le permitieron resolver el famoso problema de Basilea en 1735,[31] por el cual quedaba demostrado que:

Euler introdujo el uso de la función exponencial y de los logaritmos en las demostraciones analíticas. Descubrió formas para expresar varias funciones logarítmicas utilizando series de potencias, y definió con éxito logaritmos para números negativos y complejos, expandiendo enormemente el ámbito de la aplicación matemática de los logaritmos.[32] También definió la función exponencial para números complejos, y descubrió su relación con las funciones trigonométricas. Para cualquier número real φ, la fórmula de Euler establece que la función exponencial compleja puede establecerse mediante la siguiente fórmula:
- .
Siendo un caso especial de la fórmula (cuando = ), lo que se conoce como la identidad de Euler:
Esta fórmula fue calificada por Richard Feynman como «la fórmula más reseñable en matemáticas», porque relaciona las principales operaciones algebraicas con las importantes constantes 0, 1, , y π, mediante la relación binaria más importante.[33] En 1988, los lectores de la revista especializada The Mathematical Intelligencer votaron la fórmula como «la más bella fórmula matemática de la historia».[34] En total, Euler fue el responsable del descubrimiento de tres de las cinco primeras fórmulas del resultado de la encuesta.[34][35]
Además de eso, Euler elaboró la teoría de las funciones trascendentes (aquellas que no se basan en operaciones algebraicas) mediante la introducción de la función gamma, e introdujo un nuevo método para resolver ecuaciones de cuarto grado. También descubrió una forma para calcular integrales con límites complejos, en lo que sería en adelante el moderno análisis complejo, e inventó el cálculo de variaciones incluyendo dentro de su estudio a las que serían llamadas las ecuaciones de Euler-Lagrange.
Euler también fue pionero en el uso de métodos analíticos para resolver problemas teóricos de carácter numérico. Con ello, Euler unió dos ramas separadas de las matemáticas para crear un nuevo campo de estudio, la teoría analítica de números. Para ello, Euler creó la teoría de las series hipergeométricas, las series q, las funciones hiperbólicas trigonométricas y la teoría analítica de fracciones continuas. Por ejemplo, demostró que la cantidad de números primos es infinita utilizando la divergencia de series armónicas, y utilizó métodos analíticos para conseguir una mayor información sobre cómo los números primos se distribuyen dentro de la sucesión de números naturales. El trabajo de Euler en esta área llevaría al desarrollo del teorema de los números primos.[36]
Otros aportes[editar]
En su Introducción al análisis de los infinitos (1748), realizó el primer tratamiento analítico completo del álgebra, la teoría de ecuaciones, la trigonometría y la geometría analítica.
Trató el desarrollo de series de funciones y formuló la regla por la que solo las series convergentes infinitas pueden ser evaluadas adecuadamente. También abordó las superficies tridimensionales y demostró que las secciones cónicas se representan mediante la ecuación general de segundo grado en dos dimensiones.
Poseedor de una asombrosa facilidad para los números y el raro don de realizar mentalmente cálculos de largo alcance. Se recuerda que, en una ocasión, cuando dos de sus discípulos, al realizar la suma de unas series de diecisiete términos, no estaban de acuerdo con los resultados en una unidad de la quincuagésima cifra significativa, se recurrió a Euler. Este repasó el cálculo mentalmente, y su decisión resultó ser correcta.
Realizó también aportaciones a la astronomía, la mecánica, la óptica y la acústica. Entre sus obras más destacadas se encuentran Instituciones del cálculo diferencial (1755), Instituciones del cálculo integral (1768-1770) e Introducción al álgebra (1770).
Teoría de números[editar]
El interés de Euler en la teoría de números procede de la influencia de Christian Goldbach, amigo suyo durante su estancia en la Academia de San Petersburgo. Gran parte de los primeros trabajos de Euler en teoría de números se basan en los trabajos de Pierre de Fermat. Euler desarrolló algunas de las ideas de este matemático francés pero descartó también algunas de sus conjeturas.
Euler unió la naturaleza de la distribución de los números primos con sus ideas del análisis matemático. Demostró la divergencia de la suma de los inversos de los números primos y, al hacerlo, descubrió la conexión entre la función zeta de Riemann y los números primos. Esto se conoce como el producto de Euler para la función zeta de Riemann.
Euler también demostró las identidades de Newton, el pequeño teorema de Fermat, el teorema de Fermat sobre la suma de dos cuadrados e hizo importantes contribuciones al teorema de los cuatro cuadrados de Joseph-Louis de Lagrange. También definió la función φ de Euler que, para todo número entero positivo, cuantifica el número de enteros positivos menores o iguales a n y coprimos con n. Más tarde, utilizando las propiedades de esta función, generalizó el pequeño teorema de Fermat a lo que se conoce como el teorema de Euler.
Contribuyó de manera significativa al entendimiento de los números perfectos (teorema de Euclides-Euler), tema que fascinó a los matemáticos desde los tiempos de Euclides, y avanzó en la investigación de lo que más tarde se concretaría en el teorema de los números primos. Los dos conceptos se consideran teoremas fundamentales de la teoría de números, y sus ideas pavimentaron el camino del matemático Carl Friedrich Gauss.[37]
En el año 1772, Euler demostró que 231 – 1 = 2 147 483 647 es un número primo de Mersenne. Esta cifra permaneció como el número primo más grande conocido hasta el año 1867.[38]
Teoría de grafos y geometría[editar]

En 1736, Euler resolvió el problema conocido como problema de los puentes de Königsberg.[39] La ciudad de Königsberg, en Prusia Oriental (actualmente Kaliningrado, en Rusia), estaba localizada en el río Pregel, e incluía dos grandes islas que estaban conectadas entre ellas por un puente, y con las dos riberas del río mediante seis puentes (siete puentes en total). El problema que se planteaban sus habitantes consistía en decidir si era posible seguir un camino, y cómo hacerlo, que cruzase todos los puentes una sola vez y que finalizase llegando al punto de partida. Euler logró demostrar matemáticamente que no lo hay, porque con esta configuración no es posible conformar lo que se denomina hoy un ciclo euleriano en el grafo que modela el recorrido, debido a que el número de puentes es impar en más de dos de los bloques (representados por vértices en el grafo correspondiente).
A esta solución se la considera el primer teorema de teoría de grafos y de grafos planares.[39] Euler también introdujo el concepto conocido como característica de Euler del espacio, y una fórmula que relacionaba el número de lados, vértices y caras de un polígono convexo con esta constante: el teorema de Euler para poliedros, que básicamente consiste en buscar una relación entre número de caras, aristas y vértices en los poliedros. Utilizó esta idea para demostrar que no existían más poliedros regulares que los sólidos platónicos conocidos hasta entonces. El estudio y la generalización de esta fórmula, especialmente por Cauchy[40] y L'Huillier,[41] supuso el origen de la topología.[42][43]
Dentro del campo de la geometría analítica descubrió además que tres de los puntos notables de un triángulo —baricentro, ortocentro y circuncentro— podían obedecer a una misma ecuación, es decir, a una misma recta. A la recta que contiene el baricentro, ortocentro y circuncentro se le denomina «Recta de Euler» en su honor.
Matemática aplicada[editar]
Algunos de los mayores éxitos de Euler fueron en la resolución de problemas del mundo real a través del análisis matemático, en lo que se conoce como matemática aplicada, y en la descripción de numerosas aplicaciones de los números de Bernoulli, las series de Fourier, los diagramas de Venn, el número de Euler, las constantes e y π, las fracciones continuas y las integrales. Integró el cálculo diferencial de Leibniz con el método de fluxión de Newton, y desarrolló herramientas que hacían más fácil la aplicación del cálculo a los problemas físicos. Euler ya empleaba las series de Fourier antes de que el mismo Fourier las descubriera y las ecuaciones de Lagrange del cálculo variacional, las ecuaciones de Euler-Lagrange.
Hizo grandes avances en la mejora de las aproximaciones numéricas para resolver integrales, inventando lo que se conoce como las aproximaciones de Euler. Las más notables de estas aproximaciones son el método de Euler para resolver ecuaciones diferenciales ordinarias, y la fórmula de Euler-Maclaurin. Este método consiste en ir incrementando paso a paso la variable independiente y hallando la siguiente imagen con la derivada. También facilitó el uso de ecuaciones diferenciales, en particular mediante la introducción de la constante de Euler-Mascheroni:
Por otro lado, uno de los intereses más llamativos de Euler fue la aplicación de las ideas matemáticas sobre la música. En 1739 escribió su obra Tentamen novae theoriae musicae, esperando con ello poder incorporar el uso de las matemáticas a la teoría musical. Esta parte de su trabajo, sin embargo, no atrajo demasiada atención del público, y llegó a ser descrita como «demasiado matemática para los músicos y demasiado musical para los matemáticos».[44]
Física y astronomía[editar]
Euler ayudó a desarrollar la ecuación de la curva elástica, que se convirtió en el pilar de la ingeniería. Aparte de aplicar con éxito sus herramientas analíticas a los problemas de mecánica clásica, Euler también las aplicó sobre los problemas de los movimientos de los astros celestes. Su trabajo en astronomía fue reconocido mediante varios premios de la Academia de Francia a lo largo de su carrera, y sus aportes en ese campo incluyen cuestiones como la determinación con gran exactitud de las órbitas de los cometas y de otros cuerpos celestes, incrementando el entendimiento de la naturaleza de los primeros, o el cálculo del paralaje solar. Formuló siete leyes o principios fundamentales sobre la estructura y dinámica del Sistema Solar y afirmó que los distintos cuerpos celestes y planetarios rotan alrededor del Sol siguiendo una órbita de forma elíptica. Sus cálculos también contribuyeron al desarrollo de tablas de longitud más exactas para la navegación.[45] También publicó trabajos sobre el movimiento de la Luna.
Además, Euler llevó a cabo importantes contribuciones en el área de la óptica. No estaba de acuerdo con las teorías de Newton sobre la luz, desarrolladas en su obra Opticks, y que eran la teoría prevalente en aquel momento. Sus trabajos sobre óptica desarrollados en la década de 1740 ayudaron a que la nueva corriente que proponía una teoría de la luz en forma de onda, propuesta por Christiaan Huygens, se convirtiese en la teoría hegemónica. La nueva teoría mantendría ese estatus hasta el desarrollo de la teoría cuántica de la luz.[46]
En el campo de la mecánica Euler, en su tratado de 1739, introdujo explícitamente los conceptos de partícula y de masa puntual y la notación vectorial para representar la velocidad y la aceleración, lo que sentaría las bases de todo el estudio de la mecánica hasta Lagrange. En el campo de la mecánica del sólido rígido definió los llamados «tres ángulos de Euler para describir la posición» y publicó el teorema principal del movimiento, según el cual siempre existe un eje de rotación instantáneo, y la solución del movimiento libre (consiguió despejar los ángulos en función del tiempo).
En hidrodinámica estudió el flujo de un fluido ideal incompresible, detallando las ecuaciones de Euler de la hidrodinámica.
Adelantándose más de cien años a Maxwell previó el fenómeno de la presión de radiación, fundamental en la teoría unificada del electromagnetismo. En los cientos de trabajos de Euler se encuentran referencias a problemas y cuestiones tremendamente avanzadas para su tiempo, que no estaban al alcance de la ciencia de su época.
Lógica[editar]
En el campo de la lógica, se atribuye a Euler el uso de curvas cerradas para ilustrar el razonamiento silogístico (1768). Las representaciones de este tipo reciben el nombre de diagramas de Euler.[47]
Arquitectura e ingeniería[editar]
En este campo, Euler desarrolló la ley que lleva su nombre sobre el pandeo de soportes verticales y generó una nueva rama de ingeniería con sus trabajos sobre la carga crítica de las columnas.
Creencias religiosas y posturas filosóficas[editar]
Euler y su amigo Daniel Bernoulli se oponían al monismo de Leibniz y a la corriente filosófica representada por Christian Wolff. Euler insistía en que el conocimiento se basa en parte en la existencia de leyes cuantitativas precisas, algo que el monismo y las teorías filosóficas de Wolff no eran capaces de proveer. Sus inclinaciones religiosas también pueden haber contribuido a que le desagradase ese tipo de doctrinas, hasta el punto de que llegó a catalogar las ideas de Wolff como «paganas y ateas».[48] Sin embargo, tuvo una inmensa influencia debido al racionalismo temprano del filósofo René Descartes.
Gran parte del conocimiento que tenemos de las creencias religiosas de Euler se deduce de su obra Cartas a una Princesa alemana, así como de un trabajo anterior llamado Rettung der Göttlichen Offenbahrung Gegen die Einwürfe der Freygeister (en español, Defensa de la revelación divina frente a las objeciones de los librepensadores). Estos trabajos muestran a Euler como un cristiano convencido de que defendía la interpretación literal de la Biblia (por ejemplo, su obra Rettung era principalmente una discusión en defensa de la inspiración divina de las escrituras).[49]
Obra[editar]

Euler cuenta con una extensísima bibliografía, en esta sección se puede encontrar alguna referencia sobre algunas de sus obras más conocidas o importantes.
- Mechanica, sive motus scientia analytica exposita[50] (1736)
- Solutio problematis ad geometriam situs pertinentis (1741)
- Methodus inveniendi líneas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici latissimo sensu accepti (1744).
- Rettung der Göttlichen Offenbahrung Gegen die Einwürfe der Freygeister (Defensa de la Revelación Divina frente a las objeciones del librepensador)[51] (1747).
- Introductio in analysin infinitorum (1748)
- Institutiones Calculi Differentialis (1765)
- Theoria motus corporum solidorum seu rigidorum (1765)
- Institutiones Calculi Integralis (1768-1770)
- Vollständige Anleitung zur Algebra[52] (1770)
- Lettres à une Princesse d'Allemagne (Cartas a una Princesa alemana)[53] (1768-1772).
En 1911, la Academia Suiza de las Ciencias comenzó a publicar una colección definitiva de los trabajos de Euler titulada Opera Omnia.[26] Existe un plan para la ampliación de la obra a la publicación de la correspondencia (en el año 2008 se han publicado ya tres volúmenes de correspondencia) y los manuscritos de Euler, aunque no se ha especificado ninguna fecha para su edición.[54]
Reconocimientos y honores[editar]

- Euler es conmemorado por la Iglesia Luterana en su Calendario de Santos el 24 de mayo, en su condición de devoto cristiano (creyente en la infalibilidad de la Biblia) y de apologista convencido contrario al ateísmo creciente de su época.[49]
- Varias calles de ciudades de todo el mundo llevan su nombre, como sucede en París (Francia), Basilea (Suiza), Binzen (Alemania), México, D. F. (México), Buenos Aires (Argentina), Padua (Italia) o Englewood (Estados Unidos).[55]
- En conmemoración suya, Euler ha aparecido en la serie sexta de los billetes de 10 francos suizos.
- Numerosos sellos postales tanto suizos como alemanes y rusos llevan su efigie.
- El cráter lunar Euler recibió ese nombre en su honor.
- El asteroide (2002) Euler también debe su nombre al gran matemático.
Véase también[editar]
Notas[editar]
- ↑ Bradley, Robert E. Leonhard Euler: Life, Work and Legacy (Volumen 5 Studies in the History and Philosophy of Mathematics). Elsevier, 2007. p. 117. ISBN 9780080471297. Existen algunas dudas acerca de cómo pudo representarse el ojo derecho de Euler en el momento de pintarse el retrato. Actualmente se encuentra en el Deutsches Museum de Múnich.
- ↑ La pronunciación en el alemán regional, alemán de Basilea del siglo XVIII, debió ser diferente AFI: ['aɪləʁ].
- ↑ pronunciación de Euler
- ↑ González Redondo, Francisco A. (2003). «La contribución de Leonardo Euler a la matematización de las magnitudes y las leyes de la mecánica, 1736-1765». Llull: Revista de la Sociedad Española de Historia de las Ciencias y de las Técnicas (España: Sociedad Española de Historia de las Ciencias y de las Técnicas, SEHCYT) 26 (57): 837-858. ISSN 0210-8615. Consultado el 17 de marzo de 2021.
- ↑ a b Dunham, William (1999). Euler: The Master of Us All. The Mathematical Association of America. p. 17.
- ↑ a b c Finkel, B.F. (1897). «Biography- Leonard Euler». The American Mathematical Monthly 4 (12): 300.
- ↑ Dunham, William (1999). Euler: The Master of Us All. The Mathematical Association of America. pp. xiii. «Lisez Euler, lisez Euler, c'est notre maître à tous.»
- ↑ James, Ioan (2002). Remarkable Mathematicians: From Euler to von Neumann. Cambridge. p. 2. ISBN 0-521-52094-0.
- ↑ «Traducción al inglés por Ian Bruce del Ph.D de Euler» (pdf). Consultado el 8 de abril de 2005.
- ↑ Calinger, Ronald (1996). «Leonhard Euler: The First St. Petersburg Years (1727-1741)». Historia Mathematica 23 (2): 156.
- ↑
- ↑ Calinger, Ronald (1996). «Leonhard Euler: The First St. Petersburg Years (1727-1741)». Historia Mathematica 23 (2): 125.
- ↑ Calinger, Ronald (1996). «Leonhard Euler: The First St. Petersburg Years (1727-1741)». Historia Mathematica 23 (2): 127.
- ↑ Calinger, Ronald (1996). «Leonhard Euler: The First St. Petersburg Years (1727-1741)». Historia Mathematica 23 (2): 124.
- ↑ Calinger, Ronald (1996). «Leonhard Euler: The First St. Petersburg Years (1727-1741)». Historia Mathematica 23 (2): 128-129.
- ↑ Fuss, Nicolas. «Eulogy of Euler by Fuss». Consultado el 30 de agosto de 2006.
- ↑ «Institutiones calculi differentialis (traducción en inglés)». Consultado el 8 de abril de 2008.
- ↑ a b c Dunham, William (1999). Euler: The Master of Us All. The Mathematical Association of America. pp. xxiv-xxv.
- ↑ Frederick II of Prussia; Traducción: Richard Aldington (1927). Letters of Voltaire and Frederick the Great, Letter H 7434, 25 January 1778. New York: Brentano's.
- ↑ «Wayback Machine». web.archive.org. Archivado desde el original el 12 de febrero de 2009. Consultado el 22 de enero de 2023.
- ↑ Calinger, Ronald (1996). «Leonhard Euler: The First St. Petersburg Years (1727-1741)». Historia Mathematica 23 (2): 154-155.
- ↑ «Leonhard Euler». Archivado desde el original el 12 de febrero de 2009.
- ↑ Carl B. Boyer (2010). «XXI. La época de Euler». Historia de la matemática (10ª edición). Madrid: Alianza Editorial. pp. 554 (de 808). ISBN 978 84 206 8186 3. «En el libro se cita la frase, pero no su procedencia exacta».
- ↑ Gekker y Euler, 2007, p. 405
- ↑ Marquis de Condorcet. «Eulogy of Euler - Condorcet». Consultado el 30 de agosto de 2006.
- ↑ a b Opera Omnia en http://www.eulerarchive.org
- ↑ Mónica Salomone (26 de diciembre de 2007). «Entrevista en el periódico El País a Hanspeter Kraft». Consultado el 8 de abril de 2008. Entrevista en el periódico El País a Hanspeter Kraft
- ↑ Historia del Sudoku
- ↑ Boyer, Carl B.; Uta C. Merzbach. A History of Mathematics. John Wiley & Sons. pp. 439-445. ISBN 0-471-54397-7.
- ↑ Wolfram, Stephen. «Mathematical Notation: Past and Future». Archivado desde el original el 1 de febrero de 2009. Consultado el agosto de 2006.
- ↑ a b Wanner, Gerhard; Harrier, Ernst (March de 2005). Analysis by its history (1st edición). Springer. p. 62.
- ↑ Boyer, Carl B.; Merzbach, Uta C. A History of Mathematics. John Wiley & Sons. pp. 439-445. ISBN 0-471-54397-7.
- ↑ Feynman, Richard. «Chapter 22: Algebra». The Feynman Lectures on Physics: Volume I. pp. p.10.
- ↑ a b Wells, David (1990). «Are these the most beautiful?». Mathematical Intelligencer 12 (3): 37-41.
- ↑ Wells, David (1988). «Which is the most beautiful?». Mathematical Intelligencer 10 (4): 30-31.
Véase también *Peterson, Ivars. «The Mathematical Tourist». Archivado desde el original el 31 de marzo de 2007. Consultado el marzo de 2008. - ↑ Dunham, William (1999). «3,4». Euler: The Master of Us All. The Mathematical Association of America.
- ↑ Dunham, William (1999). «1,4». Euler: The Master of Us All. The Mathematical Association of America.
- ↑ Caldwell, Chris. «The largest known prime by year» (en inglés). The Prime Pages. Universidad de Tennessee. http://primes.utm.edu/notes/by_year.html.
- ↑ a b Alexanderson, Gerald (July de 2006). «Euler and Königsberg's bridges: a historical view». Bulletin of the American Mathematical Society.
- ↑ Cauchy, A.L. (1813). «Recherche sur les polyèdres—premier mémoire». Journal de l'Ecole Polytechnique. 9 (Cahier 16): 66-86.
- ↑ L'Huillier, S.-A.-J. (1861). «Mémoire sur la polyèdrométrie». Annales de Mathématiques 3: 169-189.
- ↑ Marta Macho Stadler. «¿Qué es la topología?» (pdf). Archivado desde el original el 9 de junio de 2004. Consultado el 10 de abril de 2005.
- ↑ David Garro Moreno. «Historia de la topología» (pdf). Archivado desde el original el 25 de octubre de 2006. Consultado el 10 de abril de 2005.
- ↑ Calinger, Ronald (1996). «Leonhard Euler: The First St. Petersburg Years (1727-1741)». Historia Mathematica 23 (2): 144-145.
- ↑ Youschkevitch, A P; Biography in Dictionary of Scientific Biography (New York 1970–1990).
- ↑ Home, R.W. (1988). «Leonhard Euler's 'Anti-Newtonian' Theory of Light». Annals of Science 45 (5): 521-533.
- ↑ Baron, M. E.; A Note on The Historical Development of Logic Diagrams. The Mathematical Gazette: The Journal of the Mathematical Association. Vol LIII, no. 383 May 1969.
- ↑ Calinger, Ronald (1996). «Leonhard Euler: The First St. Petersburg Years (1727-1741)». Historia Mathematica 23 (2): 153-154.
- ↑ a b Euler, Leonhard (1960). «Rettung der Göttlichen Offenbahrung Gegen die Einwürfe der Freygeister». En Orell-Fussli, ed. Leonhardi Euleri Opera Omnia (series 3) 12.
- ↑ «Mechanica, sive motus scientia analytica exposita» (en francés). Consultado el 8 de abril de 2008.
- ↑ Euler, Leonhard; Arana Cañedo-Argüelles, Juan (1991). Leonhard Euler, «defensa de la revelación divina contra las objeciones del librepensador». ISSN 0212-8365. Consultado el 11 de marzo de 2024.
- ↑ «Vollständige Anleitung zur Algebra» (en francés). Consultado el 8 de abril de 2008.
- ↑ «Lettres à une Princesse d'Allemagne t. 1» (en francés). Archivado desde el original el 22 de abril de 2008. Consultado el 8 de abril de 2008. «Lettres à une Princesse d'Allemagne t. 2» (en francés). Consultado el 8 de abril de 2008. «Lettres à une Princesse d'Allemagne t. 3» (en francés). Archivado desde el original el 22 de abril de 2008. Consultado el 8 de abril de 2008.
- ↑ «Información sobre la Opera Omnia y otras publicaciones de trabajos de Euler». Archivado desde el original el 28 de junio de 2010. Consultado el 8 de abril de 2008.
- ↑ Información de GoogleMaps[1] (Consultado el 23 de noviembre de 2015)
Otras lecturas[editar]
- Lexikon der Naturwissenschaftler, 2000. Heidelberg: Spektrum Akademischer Verlag.
- Demidov, S.S., 2005, «Treatise on the differential calculus» en Grattan-Guiness, I., ed., Landmark Writings in Western Mathematics. Elsevier: 191-98.
- Dunham, William (1999) Euler: The Master of Us All, Washington: Mathematical Association of America. ISBN 0-88385-328-0.
- Euler, Leonhard (1768) - Mínguez Pérez, Carlos (ed.) (1990) Cartas a una Princesa de Alemania sobre diversos temas de Física y Filosofía, Prensas de la Universidad de Zaragoza, ISBN 84-7733-145-6
- Fraser, Craig G., 2005, «Book on the calculus of variations» en Grattan-Guiness, I., ed., Landmark Writings in Western Mathematics. Elsevier: 168-80.
- Gladyshev, Georgi, P (2007) «Leonhard Euler’s methods and ideas live on in the thermodynamic hierarchical theory of biological evolution», International Journal of Applied Mathematics & Statistics (IJAMAS) 11 (N07), Special Issue on Leonhard Paul Euler’s: Mathematical Topics and Applications (M. T. A.).
- W. Gautschi (2008). «Leonhard Euler: his life, the man, and his works». SIAM Review 50 (1): 3-33. doi:10.1137/070702710.
- Heimpell, Hermann, Theodor Heuss, Benno Reifenberg (editors). 1956. Die großen Deutschen, volume 2, Berlín: Ullstein Verlag.
- Krus, D.J (2001) «Is the normal distribution due to Gauss? Euler, his family of gamma functions, and their place in the history of statistics», Quality and Quantity: International Journal of Methodology, 35: 445-46.
- Nahin, Paul (2006) Dr. Euler's Fabulous Formula, New Jersey: Princeton, ISBN 978-0-691-11822-2
- Reich, Karin, 2005, «Introduction' to analysis» en Grattan-Guiness, I., ed., Landmark Writings in Western Mathematics. Elsevier: 181-90.
- Sandifer, Edward C (2007), The Early Mathematics of Leonhard Euler, Washington: Mathematical Association of America. ISBN 0-88385-559-3
- Simmons, J (1996) The giant book of scientists: The 100 greatest minds of all time, Sydney: The Book Company.
- Singh, Simon (1997). Fermat's last theorem, Fourth Estate: New York, ISBN 1-85702-669-1
- Thiele, Rüdiger (2005). «The mathematics and science of Leonhard Euler», in Mathematics and the Historian's Craft: The Kenneth O. May Lectures, G. Van Brummelen and M. Kinyon (eds.), CMS Books in Mathematics, Springer Verlag. ISBN 0-387-25284-3.
- «A Tribute to Leohnard Euler 1707-1783». Mathematics Magazine 56 (5). November de 1983.
Enlaces externos[editar]
 Wikimedia Commons alberga una galería multimedia sobre Leonhard Euler.
Wikimedia Commons alberga una galería multimedia sobre Leonhard Euler. Wikiquote alberga frases célebres de o sobre Leonhard Euler.
Wikiquote alberga frases célebres de o sobre Leonhard Euler.- The Euler Archive
- O'Connor, John J.; Robertson, Edmund F., «Leonhard Euler» (en inglés), MacTutor History of Mathematics archive, Universidad de Saint Andrews, https://mathshistory.st-andrews.ac.uk/Biographies/Euler/.
- Artículo en la Encyclopedia Britannica
- Leonhard-Euler Artículo en la Encyclopedia Britannica 1911
- How Euler did it Página web que contiene explicaciones sobre cómo Euler resolvió diversos problemas.
- Euler Archive
- Euler Committee of the Swiss Academy of Sciences
- Tricentenario de Euler (año 2007)
- The Euler Society
- Leonhard Euler Congress 2007 — San Petersburgo, Rusia.
- "Euler - 300th anniversary lecture" Archivado el 27 de diciembre de 2008 en Wayback Machine., discurso pronunciado por Robin Wilson en Gresham College, el 9 de mayo de 2007.
- Project Euler
- Árbol de familia de Euler
- The 100 Greatest Mental Calculators
- Hombres
- Nacidos en 1707
- Fallecidos en 1783
- Físicos de Suiza
- Filósofos cristianos
- Matemáticos de Suiza del siglo XVIII
- Teóricos de números
- Geómetras
- Calculadoras humanas
- Luteranismo
- Personas ciegas
- Miembros de la Academia de Ciencias de Rusia
- Fallecidos por apoplejía
- Fallecidos por hemorragia cerebral
- Miembros de la Academia de las Ciencias de Turín
- Científicos protestantes
- Analistas matemáticos
- Matemáticos del siglo XVIII
- Protestantes de Suiza
- Nacidos en Basilea
- Fallecidos en San Petersburgo
- Santos luteranos
- Leonhard Euler















