Método de Euler

En matemática y computación, el método de Euler, llamado así en honor de Leonhard Euler, es un procedimiento de integración numérica para resolver ecuaciones diferenciales ordinarias a partir de un valor inicial dado.

El método de Euler es el más simple de los métodos numéricos resolver un problema del siguiente tipo:

$PVI = \left \{ \begin{array}{rcl} {dy\over dx} = f(x,y)\\ y(x_0) = y_0\\ y(x_i)=? \end{array} \right .$

Una descripción informal

Considere el problema de calcular la pendiente de una curva desconocida que comienza en un punto dado y safisface una cierta ecuación diferencial dada. Se puede pensar en la ecuación diferencial como una fórmula que nos permite calcular la pendiente de la recta tangente a la curva en cualquier punto de la curva, siempre que el punto se conozca.

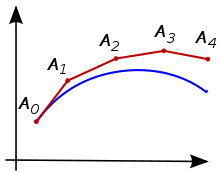
La idea es que a pesar de que la curva es desconocida en principio, su punto de comienzo(al cual denotamos por A0) es conocido. Entonces, de la ecuación diferencial se puede computar la pendiente de la curva en el punto A0 y por lo tanto la recta tangente a la curva.

Ahora, dando un pequeño paso sobre dicha recta, podemos tomarnos un nuevo punto A1 y suponer que dicho punto pertenece a la curva, entonces seguimos el mismo razonamiento aplicado anteriormente y volvemos a calcular la pendiente de la recta tangente a la curva en el punto A1. Luego de varios pasos tendremos formada una curva poligonal A0A1A2A3... En general esta curva que obtenemos al aplicar el método no diverge lejos de la curva original, además el error entre ambas curvas se puede minimizar si se dan pasos muy pequeños al avanzar sobre la recta tangente a la curva y además el intervalo sobre el que trabajamos es finito(aunque las cosas son más complicadas para ecuaciones inestables, como se discute más abajo).

Procedimiento

Consiste en dividir los intervalos que va de $x_o\,$ a $x_f\,$ en $n\,$ subintervalos de ancho $h\,$; o sea:

$h = {x_f - x_o \over n}\,$

de manera que se obtiene un conjunto discreto de $n+1 \,$ puntos: $x_o, x_1, x_2,.......,x_n\,$ del intervalo de interés $[x_o,x_f]\,$. Para cualquiera de estos puntos se cumple que:

$x_i = {x_0 + ih}, \,$ $0 \le i \le n \,$.

La condición inicial $y(x_o) = y_o \,$, representa el punto $P_o = (x_o, y_o)\,$ por donde pasa la curva solución de la ecuación de el planteamiento inicial, la cual se denotará como $F(x)= y \,$.

Ya teniendo el punto $P_o\,$ se puede evaluar la primera derivada de $F(x)\,$ en ese punto; por lo tanto:

$F'(x) = {dy\over dx} \bigg\vert\begin{matrix}\\{P_o}\end{matrix} = f(x_o,y_o)\,$

Grafica A.

Con esta información se traza una recta, aquella que pasa por $P_o\,$ y de pendiente $f(x_o, y_o)\,$. Esta recta aproxima $F(x)\,$ en una vecindad de $x_o \,$. Tómese la recta como reemplazo de $F(x) \,$ y localícese en ella (la recta) el valor de $y\,$ correspondiente a $x_1\,$. Entonces, podemos deducir según la Gráfica A:

${y_1 - y_o\over x_1 - x_o} = f(x_o,y_o) \,$

Se resuelve para $y_1\,$:

$y_1 = y_o+(x_1 - x_o) f (x_o,y_o) = y_o + h f(x_o, y_o) \,$

Es evidente que la ordenada $y_1 \,$ calculada de esta manera no es igual a $F (x_1)\,$, pues existe un pequeño error. Sin embargo, el valor $y_1 \,$ sirve para que se aproxime $F' (x) \,$ en el punto $P = (x_1,y_1)\,$ y repetir el procedimiento anterior a fin de generar la sucesión de aproximaciones siguiente:

$\begin{array}{crl} y_1 = y_o + h f (x_o,y_o)\\ y_2 = y_1 + h f (x_1,y_1)\\ .\\ .\\ .\\ y_{i+1} = y_i + h f (x_i,y_i)\\ .\\ .\\ .\\ y_n = y_{n-1} + h f (x_{n-1},y_{n-1})\\ \end{array} \quad \,$

Ejemplo

$PVI = \left \{ \begin{array}{rcl} {dy\over dx} = \sin x - \ln y\\ y(0.13) = 0.32\\ y(0.14)=? \end{array} \right .$

Calculamos el valor de $h \,$ tomando en cuenta que el $n \,$ valor de divisiones es de $4 \,$; por lo tanto quedaria así:

$h = {0.14 - 0.13 \over 4}=0.0025\,$

Antes de aplicar el método, veamos un esquema de cómo trabajaría el método en este caso concreto:

$\begin{array}{|c||c|c|} \hline {dy\over dx}& x & y \\ \hline &x_0 &y_0 \\ \hline f(x_o,y_0)=\sin(x_0)-\ln(y_0)&x_1=x_0+h &y_1=y_0+h*f(x_0,y_0) \\ \hline f(x_1,y_1)=\sin(x_1)-\ln(y_1)&x_2=x_1+h &y_2=y_1+h*f(x_1,y_1) \\ \hline f(x_2,y_2)=\sin(x_2)-\ln(y_2)&x_3=x_2+h &y_3=y_2+h*f(x_2,y_2) \\ \hline f(x_3,y_3)=\sin(x_3)-\ln(y_3)&x_4=x_3+h &y_4=y_3+h*f(x_3,y_3) \\ \hline \end{array}$

Los valores iniciales de $x \,$ y $y \,$ vienen dados por:

$x_o = 0.13 \,$, $y_o = 0.32 \,$.

Teniendo dichos valores podemos comenzar con el método. Se harán aproximaciones de hasta trece decimales. La función seno se evaluará en grados.

$\begin{array}{|c||c|c|} \hline {dy\over dx}& x & y \\ \hline &0.13 &0.32 \\ \hline \sin(0.13)-\ln(0.32)=1.1417032092692 &0.13 +0.0025=0.1325 &0.32+(0.0025*1.1417032092692)=0.322854258023173 \\ \hline \sin(0.1325)-\ln(0.322854258023173)=1.1328668303351 &0.1325+0.0025=0.135 &0.322854258023173+(0.0025*1.1328668303351)=0.32568642509901075 \\ \hline \sin(0.135)-\ln(0.32568642509901075)=1.1241764390342 &0.135+0.0025=0.1375 &0.32568642509901075+(0.0025*1.1241764390342)=0.32849686619659625 \\ \hline \sin(0.1375)-\ln(0.32849686619659625)=1.12225822270029 &0.1375+0.0025=0.14 &0.32849686619659625+(0.0025*1.12225822270029)=0.331302511753346975 \\ \hline \end{array}$

Por lo que el resultado obtenido es: $y_4 = 0.331302511753346975 \,$; posteriormente procederemos a encontrar el valor relativo entre el valor exacto de la ecuación que es ${dy\over dx} = sin x-lny = 0.3325459 \,$.

Finalmente se calcula el error relativo:

$\boldsymbol{\epsilon_r}= \left | \begin{array}{rcl} \cfrac{0.331302511753346975-0.3325459}{0.3325459}*100% \\ \end{array} \right | =0.001243388246653025=1.243388246653025*10^{-3}%$

Análisis de error para el método de Euler.

Gráfica B.

La solución de las Ecuaciones diferenciales por medio de métodos numéricos involucra varios tipos de errores:

• Error del Método (Error de Truncamiento Local y Global): Este se debe a que, cómo la aproximación de una curva mediante una línea recta no es exacta, se comete un error propio del método. En este caso, el error es de primer orden - O(h¹) -

• Local: Es la diferencia que se produce entre el valor real de la función y el aproximado mediante la recta tangente -en lugar de moverse por la curva- suponiendo que el punto desde el que partimos -donde se cruzan la curva real y la recta que la aproxima- no tiene error alguno.

• Propagado: Acumulación de errores por las aproximaciones producidas durante los pasos previos acumuladas. Es decir, ya no se supone que el punto del cual partimos -donde se cruzan la curva real y la recta que la aproxima- no tenía error sino que asumimos que dicho error existe y que se propaga de paso en paso. Dicha propagación es, en el peor de los casos, lineal.

La suma de los dos es el error global.

• Redondeo/Truncamiento: Resultado del número límite de cifras significativas que puede retener una computadora. Ya que el número de dígitos utilizados para hacer los cálculos es finito y los números representados puede que no lo sean (es decir, números con infinita cantidad de dígitos). Al limitar los números con infinita cantidad de dígitos -mediante truncamiento o redondeo- a números con finita cantidad de dígitos estamos cometiendo un error extra.

Como se muestra en la Gráfica B, básicamente el método se encarga de aproximar la curva $y = F (x) \,$ por medio de una serie de segmentos en recta.

Debido a que la aproximación de una curva por medio de una línea recta no es exacta, se comete un error derivado del método. A este error se le conoce como error de truncamiento. Este error se puede disminuir reduciendo el valor de $h \,$, pero se obtendrá un mayor número de cálculos y, por consiguiente, un error de redondeo mucho más alto.

Referencias

• Nieves, Antonio (2007). Métodos numéricos aplicados a la ingeniería. Grupo editorial Patria. ISBN 978-970-817-080-2.