Sólidos platónicos

Los sólidos platónicos o regulares son poliedros convexos tal que todas sus caras son polígonos regulares iguales entre sí, y en que todos los ángulos sólidos son iguales.[1] Reciben este nombre en honor al filósofo griego Platón (ca. 427 a. C./428 a. C.-347 a. C.), a quien se atribuye haberlos estudiado en primera instancia. También se conocen como cuerpos cósmicos, sólidos pitagóricos, poliedros platónicos o, sobre la base de propiedades geométricas, poliedros regulares convexos.
Se le atribuye la formulación de la teoría general de los poliedros regulares a Teeteto, matemático contemporáneo de Platón.[2] Están gobernados por la fórmula V+C = A+2, donde V es el número de vértices; C, número de caras y A, número de aristas, que fue descubierta por el matemático Leonhard Euler.[3]
Los sólidos platónicos son el tetraedro, el cubo (o hexaedro regular), el octaedro (o bipirámide cuadrada si se incluyera en la nomenclatura de sólidos de Johnson),[4] el dodecaedro y el icosaedro (o bipirámide pentagonal giroelongada si se incluyera en la nomenclatura de sólidos de Johnson). Esta lista es exhaustiva, ya que es imposible construir otro sólido diferente de los cinco anteriores que cumpla todas las propiedades exigidas, es decir, convexidad y regularidad.
Historia[editar]
Se desconoce con exactitud desde cuándo eran conocidas las propiedades de estos poliedros; hay referencias a unas bolas neolíticas (fechadas hacia 2000 a. C.) de piedra labrada encontradas en Escocia.[5]
Los antiguos griegos estudiaron los sólidos platónicos a fondo, y fuentes (como Proclo) atribuyen a Pitágoras su descubrimiento. Otra evidencia sugiere que solo estaba familiarizado con el tetraedro, el cubo y el dodecaedro, y que el descubrimiento del octaedro y el icosaedro pertenecen a Teeteto, un matemático griego contemporáneo de Platón. En cualquier caso, Teeteto dio la descripción matemática de los cinco poliedros y es posible que fuera el responsable de la primera demostración de que no existen otros poliedros regulares convexos.
Timeo de Locri, en el diálogo de Platón, asocia al fuego con el tetraedro; al aire, con el octaedro; al agua, con el icosaedro; a la tierra, con el cubo; e indica que como aún es posible una quinta forma (que sería el dodecaedro), Dios ha utilizado esta para el universo.[6] Una descripción detallada de los sólidos platónicos figura en Los elementos, de Euclides.
El nombre del cubo en árabe, Kaaba, nombra un santuario sumamente venerado en el islam.[7]
Clasificación[editar]
Existen únicamente cinco poliedros regulares. A continuación se dan dos demostraciones de que no pueden existir más de cinco sólidos platónicos, pero demostrar que cada uno de esos cinco es efectivamente un sólido platónico es otra cuestión, que requiere una construcción explícita.
Demostración geométrica[editar]
{3,3} Defecto 180° |
 {3,4} Defecto 120° |
 {3,5} Defecto 60° |
 {3,6} Defecto 0° |
 {4,3} Defecto 90° |
 {4,4} Defecto 0° |
 {5,3} Defecto 36° |
 {6,3} Defecto 0° |
| Un vértice es adyacente a al menos 3 caras, y debe tener un defecto angular positivo. Un defecto angular de 0º llenará el plano euclídeo con un teselado regular. | |||
El siguiente argumento es muy parecido al que da Euclides en los Elementos:
- Cada vértice del sólido tiene que ser adyacente a, al menos, tres caras.
- En cada vértice del sólido, en total, entre las caras adyacentes, la suma de los ángulos entre los lados de estas adyacentes al vértice tiene que ser estrictamente menor que 360°. El sólido restante para llegar a 360° (que tiene que ser, por tanto, estrictamente mayor que 0°) se llama defecto angular.
- Los polígonos regulares de seis o más caras tienen ángulos interiores de 120° o más, por lo que, al juntar tres o más de ellos como caras adyacentes a un vértice, el defecto angular sería 0° o menos. Por tanto, las caras tienen que ser, necesariamente, triángulos, cuadrados o pentágonos regulares. Para cada caso tenemos que:
- Caras triangulares: Cada ángulo interior de un triángulo equilátero es de 60°, por lo que alrededor de un vértice se pueden colocar 3, 4 o 5 caras con forma de triángulo antes de hacer que el defecto angular se anule o vuelva negativo. Estas opciones son, respectivamente, el tetraedro, el octaedro y el icosaedro.
- Caras cuadradas: Cada ángulo interior de un cuadrado es de 90°, por lo que sólo se pueden colocar 4 caras cuadradas alrededor de un vértice antes de hacer que el defecto angular se anule. Esta única posibilidad se corresponde con el cubo.
- Caras pentagonales: Cada ángulo interior de un pentágono regular es de 108°, por lo que sólo se pueden colocar 3 caras pentagonales alrededor de un vértice antes de que el defecto angular se vuelva negativo. Esta única posibilidad se corresponde con el dodecaedro.
Analizados todos los posibles casos, podemos concluir que no pueden existir más de cinco sólidos platónicos.
Demostración topológica[editar]

Se puede hacer una demostración puramente topológica utilizando solamente información combinatoria de los sólidos. Dado cualquier supuesto sólido platónico, podemos deformar sus aristas continuamente para que todas ellas queden dentro de un plano formando un grafo plano (ver figura). El grafo obtenido tiene tantos vértices, aristas y caras (el exterior también es una cara) como tenía el sólido. Entonces, por la fórmula de Euler en el plano tenemos que , con el número de vértices, aristas y caras, respectivamente, del grafo (y, por tanto, del sólido platónico).
Un sólido platónico, por definición, queda totalmente determinado por dos números, , el número de lados de cada cara, y el número de caras (o, equivalentemente, aristas) adyacentes a cada vértice.
Ahora, si pasamos por cada cara y contamos todos sus lados, obtendremos , con el número de lados de cada cara. Pero como cada arista es adyacente a dos caras, podemos entender que hemos contado cada arista dos veces, es decir, . Como en ambos casos hemos contado lo mismo, tenemos que , donde podemos dividir por porque siempre es mayor o igual que 3.
Si ahora pasamos por cada arista y contamos los vértices a los que es adyacente, obtendremos , pues cada arista es adyacente a exactamente dos vértices. Pero como cada vértice es adyacente a aristas por definición, hemos contado cada vértice veces y, por tanto, hemos contado . Como antes, tenemos que , donde podemos dividir por porque siempre es mayor o igual que 3.
Si ahora sustituimos y en la fórmula de Euler, tenemos que:
.
Es decir, . Como , observamos que la anterior ecuación sólo puede tener cinco soluciones enteras para : , el tetraedro; , el octaedro; , el icosaedro; , el cubo, y , el dodecaedro.
Propiedades[editar]
Regularidad[editar]
Tal y como se ha expresado para definir estos poliedros:
- Las caras de un sólido platónico son polígonos regulares iguales.
- En todos los vértices de un sólido platónico concurren el mismo número de caras y de aristas.
- Todas las aristas de un sólido platónico tienen la misma longitud.
- Todos los ángulos diedros que forman las caras de un sólido platónico entre sí son iguales.
- Todos sus vértices son convexos a los del icosaedro.
Simetría[editar]
Los sólidos platónicos tienen caracterizaciones simétricas:
- El centro de un cubo (de un hexaedro regular) es centro de simetría de dicha figura, devuelve la misma figura; pero no lo es, el centro de un tetraedro regular.[8] Todos ellos gozan respecto a un punto del espacio (centro de simetría) que equidista de sus caras, de sus vértices y de sus aristas, pero no se conserva la figura original.
- Todos ellos tienen además simetría axial respecto a una serie de ejes de simetría que pasan por el centro de simetría anterior.
- Todos ellos tienen también simetría especular respecto a una serie de planos de simetría (o planos principales), que los dividen en dos partes iguales.
Como consecuencia geométrica de lo anterior, se pueden trazar en todo sólido platónico tres esferas particulares, todas ellas centradas en el centro de simetría del poliedro:
- Una esfera inscrita, tangente a todas sus caras en su centro.
- Una segunda esfera tangente a todas las aristas en su centro.
- Una esfera circunscrita, que pase por todos los vértices del poliedro.
Proyectando los centros de las aristas de un poliedro platónico sobre su esfera circunscrita desde el centro de simetría del poliedro se obtiene una red esférica regular, compuesta por arcos iguales de círculo máximo, que constituyen polígonos esféricos regulares.
Conjugación[editar]
Si se traza un poliedro empleando como vértices los centros de las caras de un sólido platónico se obtiene otro sólido platónico, llamado conjugado o dual del primero, con tantos vértices como caras tenía el sólido inicial, y el mismo número de aristas. El poliedro conjugado de un dodecaedro es un icosaedro, y viceversa; el de un cubo es un octaedro; y poliedro conjugado de un tetraedro es otro tetraedro.
Ecuación intrisetica[editar]
El teorema de Euler para poliedros expresa una cualidad topológica de los poliedros convexos, al margen de sus medidas y formas, y de modo especial de los poliedros regulares.[9] Enuncia que el número de caras de un poliedro platónico más el número de sus vértices es igual al número de sus aristas más dos, mediante la siguiente ecuación:
Tabla comparativa[editar]
| Sólidos Platónicos | Tetraedro | Hexaedro o Cubo | Octaedro | Dodecaedro | Icosaedro |
|---|---|---|---|---|---|

|

|

|

|

| |
| Animación | 
|

|

|
|

|
| Desarrollo | 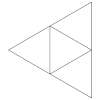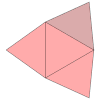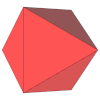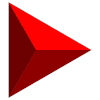
|
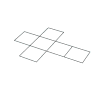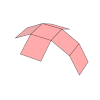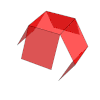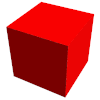
|
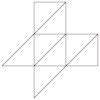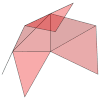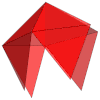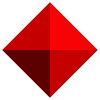
|

|

|
| Número de caras | 4 | 6 | 8 | 12 | 20 |
| Polígonos que forman las caras | Triángulos Equiláteros | Cuadrados | Triángulos Equiláteros | Pentágonos Regulares | Triángulos Equiláteros |
| Número de aristas | 6 | 12 | 12 | 30 | 30 |
| Número de vértices | 4 | 8 | 6 | 20 | 12 |
| Caras concurrentes en cada vértice | 3 | 3 | 4 | 3 | 5 |
| Vértices contenidos en cada cara | 3 | 4 | 3 | 5 | 3 |
| Grupo de simetría | Tetraédrico (Td) | Hexaédrico (Hh) | Octaédrico (Oh) | Icosaédrico (Lh) | Icosaédrico (Lh) |
| Poliedro dual | Tetraedro (autoconjugado) | Octaedro | Hexaedro, Cubo | Dodecaedro | Icosaedro |
| Símbolo de Schläfli | {3,3} | {4,3} | {3,4} | {5,3} | {3,5} |
| Símbolo de Wythoff | 3 | 2 3 | 3 | 2 4 | 4 | 2 3 | 3 | 2 5 | 5 | 2 3 |
| Ángulo diedro | 70.53° = arccos(1/3) | 90° | 109.47° = arccos(-1/3) | 116.56° | 138.189685° |
| Radio externo | |||||
| Radio interno | |||||
Poliedros regulares en la naturaleza[editar]
En la naturaleza hay estructuras que son poliedros regulares casi perfectos, por ejemplo, la estructura básica del VIH es un icosaedro regular.[10]
Bibliografía[editar]
- Sutton, David (2005). Sólidos platónicos y arquimedianos. Oniro S. A. ISBN 84-9754-131-6.
- QUINCE SALAS, Ricardo. Propiedades elementales de los poliedros regulares. Santander: [s.n.], 1974. 17 p. Comunicación presentada a las Reuniones sobre Geometría aplicada a la Arquitectura y a la Ingeniería Civil.
- QUINCE SALAS, Ricardo. Áreas y volúmenes de cuerpos geométricos. Teoría y ejercicios. Santander: Escuela Superior de Ingenieros de Caminos, Canales y Puertos, [s.a.]. 202 p.
- QUINCE SALAS, Ricardo. Áreas y volúmenes de cuerpos geométricos. Tomo 2: soluciones. Santander: Escuela Superior de Ingenieros de Caminos, Canales y Puertos, [s.a.]. 124 p.
Referencias[editar]
- ↑ Bruño, G. M.: Elementos de Geometría.
- ↑ Isaac Moisés Yaglom. La matemática real ISBN 978-5-396-00062-9, Distribuye Hayka libros desde Sevilla, España
- ↑ Boyer Historia de la Matemática
- ↑ * Norman Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pp. 169-200. Enumeración original de los 92 sólidos, y conjetura sobre que no existen otros.
- ↑ "[www.bdigital.unal.edu.co/4949/1/GloriaJudithFlórez.2011.pdf De los poliedros a los polígonos usando herramientas tecnológicas para potenciar el avance entre niveles de razonamiento geométrico]", Gloria Judith Flórez, Director: Humberto Sarria Zapata, Universidad Nacional de Colombia, Facultad de Ciencias, Departamento de Ciencias Básicas, Bogotá D.C., 2011, página 9: "Con exactitud, no se sabe en qué momento llegaron a conocerse los poliedros en la antigüedad. Los arqueólogos han hallado unas bolas labradas en piedra en Escocia (2000 a. C.) con formas de cubo, dodecaedro, icosaedro, tetraedro y octaedro (figura 1), al igual se ha hallado en Pádova (Italia 500 a. C.), un dodecaedro etrusco que probablemente era usado como juguete o decoración (figura 2)[...]". Los sólidos regulares neolíticos se encuentran en Ashmolean Museum de Oxford y fueron datados como de un período ubicado 2.000 años antes de nuestra era.
- ↑ Platón, Timeo 55a-56c.
- ↑ «Gran Enciclopedia Espasa 13» ISBN 978-9972-58-780-1
- ↑ Clemens y otros: "Geometría" ISBN 0-201-64407-X
- ↑ Tola P.: Introducción a la topología, en "La fórmula de Euler para los poliedros"
- ↑ Factores del Huésped que afectan a la progresión de la infección por el virus de la inmunodeficiencia humana de tipo 1 (VIH-1), Tesis Doctoral presentada para obtener el grado de Doctor en Ciencias Biológicas, Universidad Autónoma de Barcelona, diciembre de 2009, Anuska Llano Montero, pág. 13
Enlaces externos[editar]
 Wikimedia Commons alberga una categoría multimedia sobre Sólidos platónicos.
Wikimedia Commons alberga una categoría multimedia sobre Sólidos platónicos.












































