Tetraedro
| Tetraedro regular | ||
|---|---|---|
| Familia: Sólidos platónicos | ||
 Imagen del sólido | ||
| Caras | 4 | |
| Aristas | 6 | |
| Vértices | 4 | |
| Grupo de simetría | Tetraédrico (Td) | |
| Poliedro dual | Tetraedro regular (autoconjugado) | |
| Ángulo diedro | cos-1(13) ≈ 70.52878° | |
| Símbolo de Schläfli | {3, 3} | |
| Símbolo de Wythoff | 3 | 2 3 | |
| Propiedades | ||
| Poliedro regular convexo, deltaedro | ||

Un tetraedro (del griego τέτταρες 'cuatro' y ἕδρα 'asiento, base de apoyo o cara') o pirámide triangular es un poliedro con cuatro caras, seis aristas y cuatro vértices. Las caras de un tetraedro son triángulos y en cada vértice concurren tres caras; si las cuatro caras del tetraedro son triángulos equiláteros, iguales entre sí, el tetraedro se denomina regular. Además es un sólido platónico. De otra manera un tetraedro es una pirámide con base triangular.
El tetraedro es el más simple de todos los poliedros convexos ordinarios y el único que tiene menos de cinco caras.[1]
Otros elementos[editar]
Además de cara, vértice, arista y altura, se precisan otros elementos:
- Esfera inscrita
Es la esfera cuyo centro es interior y la esfera es tangente a las cuatro caras. Su radio se suele denotar por r.[cita requerida]
- Esfera circunscrita
Se llama así a la esfera tal que los vértices del tetraedro están en la superficie esférica y su centro es un punto interior. Su radio se suele denotar por R.[cita requerida]
- Bimediana
Es el segmento que une los puntos medios de dos aristas opuestas; se denota por mi, i = 1,...,4. La de menor longitud se escribe m.[2]
Propiedades geométricas[editar]

En todo tetraedro se verifican las siguientes propiedades:
- Los segmentos que unen los puntos medios de las aristas opuestas (bimedianas) son concurrentes en un punto; este es el punto medio de dichos segmentos.
- Los segmentos que unen cada vértice con los puntos de intersección de las medianas de su cara opuesta son también concurrentes en un punto, que los divide separando tres cuartas partes del lado del vértice respectivo (Teorema de Commandino).
- Los seis planos perpendiculares a las aristas por sus puntos medios pasan por un mismo punto, centro de la esfera circunscrita al tetraedro.
- Las rectas perpendiculares a las caras por su circuncentro son concurrentes en un punto, centro de la esfera circunscrita al tetraedro.
- Los planos bisectores de los diedros interiores de un tetraedro concurren en un punto equidistante (incentro) de las cuatro caras, centro de la esfera inscrita al tetraedro.
- El plano que pasa por una arista y por el punto medio de la arista opuesta biseca el tetraedro regular en dos figuras congruentes. El volumen de cada parte es la mitad del volumen de la figura original.[3]
- El tetraedro tiene característica de Euler 2.[4]
- Las bimedianas se cortan en un punto interior llamado centro de masas, y se bisecan mutuamente.
Propiedades métricas[editar]
Volumen[editar]
El volumen de un tetraedro es
- V = , siendo B el área de una cara y h la altura del tetraedro, o sea el segmento perpendicular al plano de la base desde el vértice opuesto.
El volumen de un tetraedro de altura y base regular de lado es[5]
Recurso de geometría analítica del espacio[editar]
Existe una fórmula general para calcular del volumen de un tetraedro OABC, donde O coincide con el origen de coordenadas, sea o no regular, en función de las coordenadas cartesianas (x, y, z) de tres de sus vértices, A, B, C:
Esta fórmula también se puede escribir en términos de las coordenadas cartesianas de los cuatro vértices ; el volumen de un tetraedro (regular o no) viene dado por la siguiente fórmula:
Otra fórmula, que puede obtenerse de la anterior, permite calcular el volumen de un tetraedro, regular o irregular, conociendo la longitud de dos aristas opuestas y , la distancia y el ángulo entre ellas:
Esta fórmula es aplicable para calcular, de forma aproximada, el volumen de un terraplén, de una carretera o una presa de materiales sueltos, por ejemplo, a partir de la longitud de su coronación , la longitud en la base y su altura.

La generalización de la fórmula de Herón permite calcular el volumen de un tetraedro a partir de la medida de sus aristas a, b, c, ab, ac y bc:
u, v y w son los vectores determinados por las aristas a, b y c. Se tiene en cuenta la fórmula .
Alturas del tetraedro[editar]
Un tetraedro (no necesariamente regular) se define en ℝ3 conociendo las coordenadas de sus cuatro vértices, por ejemplo . Cualquiera de sus cuatro caras se define por el triángulo formado por los tres vértices de la misma, cada una de las caras define un plano (plano por tres puntos) base de la altura que forma con el vértice opuesto, siendo dicho vértice opuesto el punto restante que no se usó al definir la cara.
Se puede imaginar un tetraedro pensando en que su base está definida por el triángulo formado por tres vértices cualquiera del mismo a los que llamaremos y y que existe un vértice opuesto a esa base al que llamaremos .
Para calcular la altura que forma un vértice opuesto cualquiera con su cara base solo hay que poner los valores de dicho vértice opuesto en y después poner los valores de los tres vértices de la cara opuesta al mismo en y , luego aplicarlos en la fórmula siguiente:
Para conocer las cuatro alturas del tetraedro basta con ir rotando las coordenadas de sus vértices. Esta fórmula no requiere que el tetraedro sea regular, vale para cualquier tetraedro no degerado.
Tetraedro regular[editar]
Es un poliedro formado por cuatro caras que son triángulos equiláteros, y cuatro vértices en cada uno de los cuales concurren tres caras. Es uno de los cinco poliedros perfectos llamados sólidos platónicos. Además es uno de los ocho poliedros convexos denominados deltaedros. Aplicándole la nomenclatura estándar de los sólidos de Johnson podría ser denominado pirámide triangular.
- es la expresión Geométrica que representa la cantidad de caras aristas y vértices que posee el tetraedro regular. Este posee en el superíndice izquierdo seis (6) aristas uniformes de categoría planas, el numeredro indica cuatro caras uniforme (4) y el polígono básico (3) indican que este poliedro posee caras triangulares equiláteras congruentes entre sí. Cuando interpretamos los números colocados en el par poliédrico 4(3, 3) que simboliza al tetraedro, leemos que existen cuatro vértices uniformes y que cada vértices se unen tres triángulos equiláteros uniforme.
Para la escuela pitagórica el tetraedro representaba el elemento fuego, puesto que pensaban que las partículas (átomos) del fuego tenían esta forma.
Diversas medidas usando la arista[editar]
Exclusivamente a partir de la arista a se pueden calcular el resto de las dimensiones fundamentales de un tetraedro regular. Así, para las esferas singulares del tetraedro:
- Radio R de la esfera circunscrita al tetraedro (la que contiene en su superficie los cuatro vértices del mismo):
- Radio r de la esfera inscrita al tetraedro (la tangente a las cuatro caras del tetraedro):
- Radio ρ de la esfera tangente a las seis aristas del tetraedro:
En un tetraedro regular cada pareja de aristas opuestas (las que no concurren en un mismo vértice) son ortogonales entre sí, siendo la mínima distancia entre ellas el segmento que une sus puntos medios, de longitud doble al radio ρ de la esfera tangente a las aristas del tetraedro.
- La altura H del tetraedro regular (apoyado el tetraedro de manera estable sobre un plano horizontal, distancia perpendicular desde el plano de apoyo al vértice opuesto):[6][7]
Volumen, área y desarrollo[editar]
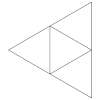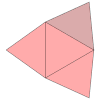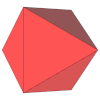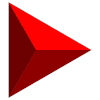
Dado un tetraedro regular de arista a, podemos calcular su volumen V mediante la siguiente fórmula:[6][8]
Y el área total de sus caras A (que es 4 veces el área de una de ellas, Ac), mediante:[6][8]
Ángulos[editar]
Los ángulos planos que forman las aristas concurrentes son, como en el resto de los sólidos platónicos, todos iguales; y con un valor de 60° (π/3 rad), al constituir los ángulos interiores de un triángulo equilátero.
Los ángulos diedros que forman las caras son, como en el resto de los sólidos platónicos, todos iguales, y pueden calcularse:
Los ángulos sólidos que forman los vértices son, como en el resto de los sólidos platónicos, todos iguales, y pueden calcularse:
Propiedades particulares[editar]
Simetría[editar]


Un tetraedro regular tiene cuatro ejes de simetría de orden tres, las rectas perpendiculares a cada cara por el vértice opuesto de tetraedro; y seis planos de simetría, los formados por cada arista y el punto medio de la arista opuesta. Esto hace que este cuerpo tenga un orden de simetría total de 24: 2x(4x3).
Los elementos de simetría anteriores definen uno de los grupos de simetría tetraédricos, el denominado Td según la notación de Schläfli.
El tetraedro tiene también tres ejes de simetría de orden dos: las rectas que pasan por el punto medio de una arista y por el de la arista opuesta.
- Un plano que pasa por una arista y el punto medio de la arista opuesta de un tetraedro regular es un plano de simetría del tetraedro regular.En total hay 6 planos de simetría.[9]
Conjugación[editar]
El tetraedro regular es el único sólido platónico conjugado de sí mismo (se suele denominar autoconjugado), ya que el poliedro conjugado de un tetradro de arista a es otro tetraedro de arista b, tal que:
Proyecciones[editar]
Las proyecciones ortogonales de un tetraedro regular sobre un plano pueden ser:
- Triángulos;
- En particular, si el plano de proyección es paralelo a una cara, la proyección del tetraedro es un triángulo equilátero, correspondiente a una cara en verdadera magnitud.
- Cuadriláteros;
- En particular, si el plano de proyección es paralelo a dos aristas opuestas del tetraedro, la proyección es un cuadrado, con un lado igual a la longitud de la arista del tetraedro dividida por la raíz cuadrada de dos.
Secciones[editar]

Las infinitas secciones que podemos tomar de un tetraedro regular pueden resultar:
- Triángulos;
- En particular, cualquier sección tomada por un plano paralelo a una de las caras del tetraedro es un triángulo equilátero.
- Cuadriláteros;
- En particular, cualquier sección tomada por un plano paralelo a dos aristas opuestas es un rectángulo.
- Si, además de ser paralelo a dos aristas opuestas, el plano de corte equidista de ambas, la sección resultante es un cuadrado de lado mitad de la arista del tetraedro. Como existen tres pares de aristas opuestas, un tetraedro regular se puede seccionar de esta forma por tres planos diferentes.
Composición, descomposición y maclado[editar]
Es posible incluir un tetraedro regular en un cubo de tal forma que cada uno de los vértices del tetraedro coincida con un vértice del cubo, coincidiendo las aristas del tetraedro con diagonales de las caras del cubo. El volumen del cubo necesario para incluir un tetraedro en la forma descrita es el triple que el del tetraedro. Hay dos posiciones posibles para incluir los tetraedros en el cubo en esta forma;
- Las aristas de los tetraedros colocados en ambas posiciones son perpendiculares entre sí (son las diagonales cruzadas de las caras del cubo).
- Las tres secciones cuadradas de ambos tetraedros coinciden.
- El sólido conjunto (o macla) de ambas es un poliedro compuesto denominado estrella octángula de Kepler (stella octangula).
- El sólido común de ambos es un octaedro regular de arista mitad que la de los tetraedros.
No es posible rellenar el espacio únicamente con tetraedros regulares (aunque, parece ser, que Aristóteles así lo creía), pero sí es posible hacerlo con elementos formados por una combinación de un octaedro regular y dos tetraedros regulares.
De las infinitas formas de truncar un tetraedro regular, hay dos que producen resultados singulares:
- Truncando el tetraedro con planos que pasen por el punto medio de sus aristas, obtenemos un octaedro regular.
- Truncando el tetraedro con planos que pasen por la tercera parte de sus aristas, obtenemos un sólido arquimediano que toma el nombre genérico de tetraedro truncado.
Un tetraedro no puede ser estrellado, puesto que todas las intersecciones entre los planos de las caras del tetraedro son aristas del tetraedro.
Tetraedros en la naturaleza y en la técnica[editar]

La forma tetraédrica aparece en la naturaleza en ciertas moléculas de enlace covalente. La más común de ellas es la molécula de metano (CH4), en la que los cuatro átomos de hidrógeno se sitúan aproximadamente en los cuatro vértices de un tetraedro regular del que el átomo de carbono es el centro.
Existen también estructuras cristalinas naturales de forma tetraédrica.
A pesar de ser el tetraedro un poliedro de forma simple y totalmente regular no existen muchos objetos de uso común basados en su forma.
Como medio de almacenamiento es una forma desastrosa: no es posible rellenar el espacio con ella, que sería la forma de no desperdiciar volumen entre las piezas; tampoco resulta fácilmente apilable al no tener caras paralelas; y, además, es muy ineficaz: para contener un litro de producto son necesarios más de 7,2 dm² de «pared», mientras que utilizando un cubo con 6 dm² es suficiente. A pesar de todos estos inconvenientes, la empresa sueca Tetra Pak desarrolló un envase de cartón metalizado en forma tetraédrica en la década de 1950, únicamente porque su fabricación resultaba singularmente sencilla: bastaba con enrollar una hoja de papel formando un cilindro, para después aplastar sus dos extremos, pero en direcciones perpendiculares, logrando con ello un tetraedro.
En cualquier posición que sea apoyado un tetraedro, uno de sus vértices queda vertical hacia arriba. Por este motivo se basa en su forma la fabricación de ciertos modelos de elementos móviles de balizamiento de carreteras ya que, al ser indiferente la posición en la que se apoyen, su colocación es rápida y sencilla, y no pueden ser derribados por los vehículos.

Es una forma sencilla con gran facilidad para trabarse y engancharse, puesto que sus vértices son muy agudos y dirigidos en las cuatro direcciones. Por este motivo se busca su forma en elementos cuya principal función sea engancharse, como las anclas de barco (en esquema, un ancla está formada por las dos aristas opuestas de un tetraedro unidas por su perpendicular), o trabarse entre sí, como las escolleras de hormigón armado para defensa contra el oleaje. Existen al menos tres modelos de uso frecuente basados en la forma de un tetraedro regular:
- Los tetrápodos, formados por cuatro troncos de cono colocados según las alturas de un tetraedro regular, entre sus vértices y su centro.

- Los doloses (plural de dolos), diseñados por el ingeniero Eric M. Merrifield, formados por tres piezas rectas, dos materializando las aristas opuestas de un tetraedro regular y una tercera uniéndolas por su perpendicular.
- Los akmon (yunque), desarrollados en el Laboratorio de Hidráulica de Delf (Países Bajos), de forma similar a los doloses, pero más robusta.
A principios del siglo XX Alexander Graham Bell, inventor del teléfono, experimentó intensamente con cometas, con el fin de desarrollar el vuelo tripulado con vehículos más pesados que el aire, y llegó tras una serie de experimentos a esta forma.
Las cometas tetraédricas están compuestas de múltiples celdas con forma de tetraedro, en el que se materializan únicamente dos de sus caras. Llegó a construir cometas enormes, formadas por un gran número de estas celdas.

En 1907 construyó una de 3.393 celdas que arrastró con un barco de vapor, siendo capaz de elevarla 50 m con un tripulante a bordo. Intentó después otras construcciones aún más grandes, y equipadas con motor, pero no dieron el resultado deseado. A los motores les faltaba potencia y las construcciones resultaban frágiles en exceso, por lo que abandonó el proyecto, dedicándose a otras actividades.
La sonda espacial Mars Pathfinder de la NASA también tuvo forma de tetraedro, cuyas caras se abrieron como pétalos al amartizar, el 4 de julio de 1997, para permitir la salida del robot Sojourner que llevaba en su interior.
Otra aplicación práctica del tetraedro es la de dar forma al dado de cuatro caras, cuya notación escrita es «d4»[10] y al que se utiliza sobre todo en numerosos juegos de rol. Al no mostrar este dado una cara hacia arriba, suele llevar marcado el valor de la tirada en los vértices o en la base.
Poliedros relacionados[editar]
| Pirámides | ||||||||
|---|---|---|---|---|---|---|---|---|
| Digonal | Triangular | Cuadrada | Pentagonal | Hexagonal | Heptagonal | Octogonal | Eneagonal | Decagonal... |
| Impropia | Regular | Equilátera | Isósceles | |||||

|

|

|

| |||||

|

|

|

|

|

|

|

|

|
Véase también[editar]
Referencias[editar]
- ↑ Weisstein, Eric W. «Tetrahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ S. V. Gashkov: Desigualdades geométricas, Editorial URSS, Moscú- 2015
- ↑ Elementos de Geometría de Bruño
- ↑ Shishkin: Característica de Euler
- ↑ Sapiña, R. «Área y volumen de un tetraedro». Problemas y ecuaciones. ISSN 2659-9899. Consultado el 9 de julio de 2020.
- ↑ a b c Llopis, José L. «Calcular área y volumen del tetraedro regular». Matesfacil. ISSN 2659-8442. Consultado el 6 de septiembre de 2020.
- ↑ Köller, Jürgen, "Tetrahedron", Mathematische Basteleien, 2001
- ↑ a b Coxeter, Harold Scott MacDonald; Regular Polytopes, Methuen and Co., 1948, Table I(i)
- ↑ Claudi Alsina 'Las mil caras de la belleza geométrica Los poliedros, 2011, Barcelona, impreso por Novagrafik ISBN 978-84-9006-022-3
- ↑ Dice-Play, página web especializada en juegos basados en el uso de dados (en inglés)
Bibliografía complementaria[editar]
- Ball, W. W. Rouse; Coxeter, H. S. M. (1987). Mathematical recreations and essays (en inglés) (13.ª edición). Nueva York: Dover Publications. ISBN 0486253570.
- Campos Newman, Luis E.; Raeder Vogel, Pablo H. (1982). Geodésicas: trazo básico. México: Universidad Iberoamericana. ISBN 968859198X.
- Coxeter, H. S. M. (1961). Introduction to geometry (en inglés). Nueva York: John Wiley & Sons. ISBN 0471504580.
- ——— (1971). Fundamentos de geometría. México: Editorial Limusa-Wiley.
- ——— (1973). Regular polytopes (en inglés) (3.ª edición). Nueva York: Dover Publications. ISBN 0486614808.
- Critchlow, Keith (1970). Order in space: a design source book (en inglés). Nueva York: Viking Press.
- Cromwell, Peter R. (1997). Polyhedra (en inglés). Cambridge: Cambridge University Press. ISBN 0521664055.
- Cundy, Henry Martyn; Rollett, Arthur Percy (1961). Mathematical models (en inglés) (2.ª edición). Londres: Oxford University Press.
- Hilbert, David; Cohn-Vossen, Stephan (1944). Anschauliche Geometrie (en alemán).
- ———; ——— (1952). Geometry and the imagination (en inglés). Trad. por P. Nemenyi. New York: Chelsea Publishing Company. ISBN 0821819984.
- Holden, Alan; Morrison (née Singer), Phylis (1982). Crystals and crystal growing (en inglés). Cambridge: The MIT Press. ISBN 0262580500.
- ——— (1971). Shapes, space and symmetry (en inglés). Nueva York: Columbia University Press. ISBN 0486268519.
- Kappraff, Jay (2001). Connections: the geometric bridge between art and science. Series on Knots and Everything (en inglés). Vol. 25 (2.ª edición). Singapur: World Scientific Publishing. ISBN 9810245858.
- Pugh, Anthony (1976). Polyhedra: a visual approach (en inglés). Berkeley: University of California Press. ISBN 0520030567.
- Sutton, Daud (2002). Platonic & Archimedean solids. Wooden Books (en inglés). Walker & Company. ISBN 0802713866.
- ——— (2005). Sólidos platónicos y arquimedianos. La aventura de la ciencia. Vol. 6. Ediciones Oniro. ISBN 8497541316.
- Wenninger, Magnus J. (1974). Polyhedron models (en inglés). Londres: Cambridge University Press. ISBN 0521098599.
- Williams, Robert W. (1979). The geometrical foundation of natural structure: a source book of design (en inglés). Nueva York: Dover Publications. ISBN 048623729X.
- Claudi Alsina: Las mil caras del poliedro 2014
Enlaces externos[editar]
 Wikimedia Commons alberga una categoría multimedia sobre Tetraedro.
Wikimedia Commons alberga una categoría multimedia sobre Tetraedro. Wikcionario tiene definiciones y otra información sobre tetraedro.
Wikcionario tiene definiciones y otra información sobre tetraedro.- Hart, George W. «The Five Platonic Solids». Virtual Polyhedra (en inglés). Consultado el 20 de junio de 2013. Sitio con miles de poliedros mostrados en realidad virtual.
- Maeder, Roman E. «Tetrahedron». The Uniform Polyhedra (en inglés). Consultado el 20 de junio de 2013. Sitio con una lista de los 75 poliedros uniformes.
- Weisstein, Eric W. «Tetrahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Regular Tetrahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.

































