Poliedro convexo
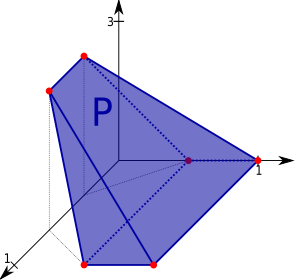
Un poliedro convexo es un politopo tridimensional cuyo interior describe un conjunto convexo. Un poliedro convexo cumple con la propiedad de que, para cualquier segmento, si sus extremos se encuentran en el interior del poliedro, el resto del segmento también lo está.
Definiciones[editar]
Definición 1[editar]
Un poliedro es convexo si cumple que, si se traza un plano que contiene una de sus caras, el poliedro queda totalmente contenido en uno de los semiespacios y en el plano trazado.[1]
Definición 2[editar]
Para todo poliedro convexo de s caras existe una matriz de s filas y tres columnas M y un vector b de s componentes:
tales que las coordenadas cartesianas de los puntos de su interior satisfacen el sistema de desigualdades lineales:
donde . Cada una de las s ecuaciones exige que los puntos se encuentren en el lado correcto del plano que contiene a la cara. Las soluciones de un sistema de la forma cuando los elementos de la matriz ' y del vector son números reales arbitrarios no es siempre un poliedro. Para serlo tanto como han de satisfacer ciertas condiciones.
Relación fundamental[editar]
Para un poliedro convexo con un número finito de vértices, la característica de Euler debe coincidir con la de la esfera, es válida la siguiente fórmula entre el número de vértices (V), aristas (A) y caras (C):
Referencias[editar]
- ↑ A. Pogorelov Geometry Mir Publishers Moscow (1987)
Véase también[editar]
Enlaces externos[editar]
- Weisstein, Eric W. «Poliedro convexo». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Komei Fukuda, Cómputos de los poliedros








