Pirámide cuadrada
| Pirámide cuadrada | ||
|---|---|---|
| Familia: Sólidos de Johnson | ||
 Imagen del sólido | ||
| Caras |
4 triángulos 1 cuadrado | |
| Aristas | 8 | |
| Vértices | 5 | |
| Configuración de vértices |
4(32.4) (34) | |
| Grupo de simetría | C4v | |
| Poliedro dual | autodual | |
| Propiedades | ||
| convexo | ||
| Desarrollo | ||
 | ||
En geometría, una pirámide cuadrada o pirámide cuadrangular es una pirámide de base cuadrada, a diferencia del tetraedro, cuya base es triangular. Si la cúspide está situada exactamente sobre el centro del cuadrado (pirámide recta),.
Sólido de Johnson (J1)
[editar]
Derecha: Pirámide con volumen máximo para una superficie dada

Si todas las caras son triángulos equiláteros, entonces la pirámide es uno de los sólidos de Johnson (J1). En este caso, todas las aristas tienen la misma longitud.[1]
La pirámide cuadrada de Johnson se puede caracterizar por un solo parámetro, que es la longitud de una de sus aristas a. La altura H (del punto central del cuadrado a la cúspide), el área total A y el volumen V de la pirámide son[2]
Volumen máximo para una superficie dada
[editar]Entre todas las pirámides cuadradas con una superficie dada (que incluye las cuatro caras laterales y el área de la base), la que contiene el mayor volumen mide:
- y por lo tanto
Su volumen es entonces .
La altura de esta pirámide es el doble de la altura de la pirámide de Jhonson cuadrada.
Para probarlo, basta plantaer la ecuación para teniendo en cuenta que y determinar el máximo local de .
Otras pirámides cuadradas
[editar]Otras pirámides cuadradas tienen caras que son triángulos isósceles. Un ejemplo es la Gran Pirámide de Guiza, cuyos triángulos tienen una longitud de base de 230 metros y una altura inclinada de 219 metros. Dicha pirámide tiene la curiosa propiedad de que la proporción entre la altura inclinada (a lo largo de la bisectriz de la cara) y la altura se aproxima muy bien a la razón áurea, por lo que el área de cada una de las caras triangulares es igual al cuadrado de la altura de la pirámide
En las pirámides cuadradas rectas en general, si el lado de base mide y su altura es , el área y el volumen se calculan según las expresiones siguientes:[3]
La fórmula anterior del volumen es también válida para el caso de las pirámides oblicuas, por el principio de Cavalieri.
Poliedros relacionados
[editar]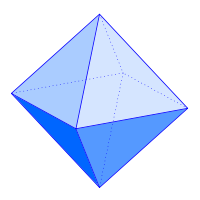
|
|
|---|---|
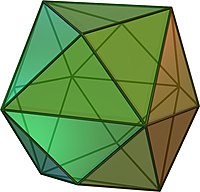
| Un octaedro regular se puede considerar una bipirámide cuadrada que se compone de dos Johnson pirámides cuadradas conectadas base a base. | El tetraquis hexaedro se puede considerar un cubo a cada una de cuyas caras se añaden pirámides cuadradas chatas. |
| Pirámides | ||||||||
|---|---|---|---|---|---|---|---|---|
| Digonal | Triangular | Cuadrada | Pentagonal | Hexagonal | Heptagonal | Octogonal | Eneagonal | Decagonal... |
| Impropia | Regular | Equilátera | Isósceles | |||||

|

|

|

| |||||

|

|

|

|

|

|

|

|

|
Topología
[editar]Al igual que cualquier pirámide, la pirámide cuadrada es autodual, al contener el mismo número de vértices y caras.
Una pirámide cuadrada puede representarse por el grafo de rueda W5.
Véase también
[editar] Portal:Matemática. Contenido relacionado con Matemática.
Portal:Matemática. Contenido relacionado con Matemática. Portal:Geometría. Contenido relacionado con Geometría.
Portal:Geometría. Contenido relacionado con Geometría.
Referencias
[editar]- ↑ Hocevar, Franz (1903). A. & C. Black, ed. Solid Geometry. p. 44.
- ↑ Sapiña, R. «Sólido de Johnson J₁». Problemas y ecuaciones. ISSN 2659-9899. Consultado el 26 de junio de 2020.
- ↑ Sapiña, R. «Calculadora del área y volumen de la pirámide cuadrada». Problemas y ecuaciones. ISSN 2659-9899. Consultado el 26 de junio de 2020.
Enlaces externos
[editar]- Weisstein, Eric W. «Square pyramid». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Johnson solid». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Wheel graph». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Square Pyramid -- Interactive Polyhedron Model
- Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra (VRML model Archivado el 18 de febrero de 2012 en Wayback Machine.)















