Derivada
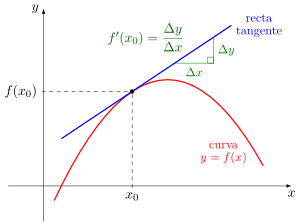
En cálculo diferencial y análisis matemático, la derivada de una función es la razón de cambio instantánea con la que varía el valor de dicha función matemática, según se modifique el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño.[1] Por eso se habla del valor de la derivada de una función en un punto dado.
Un ejemplo habitual aparece al estudiar el movimiento: si una función representa la posición de un objeto con respecto al tiempo, su derivada es la velocidad de dicho objeto para todos los momentos. Un avión que realice un vuelo transatlántico de 4500 km entre las 12:00 y las 18:00, viaja a una velocidad media de 750 km/h. Sin embargo, puede estar viajando a velocidades mayores o menores en distintos tramos de la ruta. En particular, si entre las 15:00 y las 15:30 recorre 400 km, su velocidad media en ese tramo es de 800 km/h. Para conocer su velocidad instantánea a las 15:20, por ejemplo, es necesario calcular la velocidad media en intervalos de tiempo cada vez menores alrededor de esta hora: entre las 15:15 y las 15:25, entre las 15:19 y las 15:21.
Entonces el valor de la derivada de una función en un punto puede interpretarse geométricamente, ya que se corresponde con la pendiente de la recta tangente a la gráfica de la función en dicho punto. La recta tangente es, a su vez, la gráfica de la mejor aproximación lineal de la función alrededor de dicho punto. La noción de derivada puede generalizarse para el caso de funciones de más de una variable con la derivada parcial y el diferencial.
Historia de la derivada[editar]
Los problemas típicos que dieron origen al cálculo infinitesimal comenzaron a plantearse en la época clásica de la antigua Grecia (siglo III a. C.), pero no se encontraron métodos sistemáticos de resolución hasta diecinueve siglos después (en el siglo XVII por obra de Isaac Newton y Gottfried Leibniz).
En lo que atañe a las derivadas existen dos conceptos de tipo geométrico que le dieron origen:
- El problema de la tangente a una curva (Apolonio de Perge)
- El Teorema de los extremos: máximos y mínimos (Pierre de Fermat)
En su conjunto dieron origen a lo que actualmente se conoce como cálculo diferencial.
Siglo XVII[editar]
Los matemáticos perdieron el miedo que los griegos les habían tenido a los infinitesimales: Johannes Kepler y Bonaventura Cavalieri fueron los primeros en usarlos, empezaron a andar un camino que llevaría en medio siglo al descubrimiento del cálculo infinitesimal.
A mediados del siglo XVII las cantidades infinitesimales fueron cada vez más usadas para resolver problemas de cálculos de tangentes, áreas, volúmenes; los primeros darían origen al cálculo diferencial, los otros al integral.
Newton y Leibniz[editar]
A finales del siglo XVII se sintetizaron en dos conceptos los algoritmos usados por sus predecesores, en lo que hoy llamamos «derivada» e «integral». La historia de la matemática reconoce que Isaac Newton y Gottfried Leibniz son los creadores del cálculo diferencial e integral. Ellos desarrollaron reglas para manipular las derivadas (reglas de derivación) e Isaac Barrow demostró que la derivación y la integración son operaciones inversas.
Newton desarrolló en Cambridge su propio método para el cálculo de tangentes. En 1665 encontró un algoritmo para derivar funciones algebraicas que coincidía con el descubierto por Fermat. A finales de 1665 se dedicó a reestructurar las bases de su cálculo, intentando desligarse de los infinitesimales, e introdujo el concepto de fluxión, que para él era la velocidad con la que una variable «fluye» (varía) con el tiempo.
Gottfried Leibniz, por su parte, formuló y desarrolló el cálculo diferencial en 1675. Fue el primero en publicar los mismos resultados que Isaac Newton descubriera 10 años antes, de manera independiente. En su investigación conservó un carácter geométrico y trató a la derivada como un cociente incremental y no como una velocidad, viendo el sentido de su correspondencia con la pendiente de la recta tangente a la curva en dicho punto.
Leibniz es el inventor de diversos símbolos matemáticos. A él se deben los nombres de: cálculo diferencial y cálculo integral, así como los símbolos de derivada y el símbolo de la integral ∫.
Conceptos y aplicaciones[editar]
El concepto de derivada es uno de los conceptos básicos del análisis matemático. Los otros son los de integral definida e indefinida, sucesión; sobre todo, el concepto de límite. Este es usado para la definición de cualquier tipo de derivada y para la integral de Riemann, sucesión convergente y suma de una serie y la continuidad. Por su importancia, hay un antes y un después de tal concepto que biseca las matemáticas previas, como el álgebra, la trigonometría o la geometría analítica, del cálculo. Según Albert Einstein, el mayor aporte que se obtuvo de la derivadas fue la posibilidad de formular diversos problemas de la física mediante ecuaciones diferenciales [cita requerida].
La derivada es un concepto que tiene variadas aplicaciones. Se aplica en aquellos casos donde es necesario medir la rapidez con que se produce el cambio de una magnitud o situación. Es una herramienta de cálculo fundamental en los estudios de Física, Química y Biología, o en ciencias sociales como la Economía y la Sociología. Por ejemplo, cuando se refiere a la gráfica de dos dimensiones de , se considera la derivada como la pendiente de la recta tangente del gráfico en el punto . Se puede aproximar la pendiente de esta tangente como el límite cuando la distancia entre los dos puntos que determinan una recta secante tiende a cero, es decir, se transforma la recta secante en una recta tangente. Con esta interpretación, pueden determinarse muchas propiedades geométricas de los gráficos de funciones, tales como monotonía de una función (si es creciente o decreciente) y la concavidad o convexidad.
Algunas funciones no tienen derivada en todos o en alguno de sus puntos. Por ejemplo, una función no tiene derivada en los puntos en que se tiene una tangente vertical, una discontinuidad o un punto anguloso. Afortunadamente, gran cantidad de las funciones que se consideran en las aplicaciones prácticas son continuas y su gráfica es una curva suave, por lo que es susceptible de derivación.
Las funciones que son diferenciables (derivables si se habla en una sola variable), son aproximables linealmente.
Definiciones de derivada[editar]
Derivada en un punto a partir de cocientes diferenciales[editar]

La derivada de una función en el punto es la pendiente de la recta tangente a la gráfica de en el punto . El valor de esta pendiente será aproximadamente igual a la pendiente de una recta secante a la gráfica que pase por el punto y por un punto cercano ; por conveniencia suele expresarse , donde es un número cercano a 0. A partir de estos dos puntos se calcula la pendiente de la recta secante como
(Esta expresión se denomina «cociente diferencial» o «cociente de Newton».[2]) A medida que el número se acerca a cero, el valor de esta pendiente se aproximará mejor al de la recta tangente. Esto permite definir la derivada de la función en el punto , denotada como , como el límite de estos cocientes cuando tiende a cero:
- .
No obstante, esta definición sólo es válida cuando el límite es un número real: en los puntos donde el límite no existe, la función no tiene derivada.

Derivada de una función[editar]

Dada una función , se puede definir una nueva función que, en cada punto , toma el valor de la derivada . Esta función se denota y se denomina función derivada de o simplemente derivada de . Esto es, la derivada de es la función dada por
- .
Esta función sólo está definida en los puntos del dominio de donde el límite existe; en otras palabras, el dominio de está contenido en el de .
Ejemplos[editar]
Considere la función cuadrática definida para todo . Se trata de calcular la derivada de esta función aplicando la definición
- Para el caso general tendríamos
- Teniendo en cuenta el teorema del binomio;
- Tenemos;
Continuidad y diferenciabilidad[editar]
La continuidad es necesaria[editar]
Para que una función sea derivable en un punto es necesario que también sea continua en ese punto: intuitivamente, si la gráfica de una función está «rota» en un punto, no hay una manera clara de trazar una recta tangente a la gráfica. Más precisamente, esto se debe a que, si una función no es continua en un punto , entonces la diferencia entre el valor y el valor en un punto cercano no va a tender a 0 a medida que la distancia entre los dos puntos tiende a 0; de hecho, el límite no tiene por qué estar bien definido si los dos límites laterales no son iguales. Tanto si este límite no existe como si existe pero es distinto de 0, el cociente diferencial
no tendrá un límite definido.

Como ejemplo de lo que ocurre cuando la función no es continua, se puede considerar la función de Heaviside, definida como
Esta función no es continua en : el valor de la función en este punto es 1, pero en todos los puntos a su izquierda la función vale 0. En este caso, el límite por la izquierda de la diferencia es igual a 1, por lo que el cociente diferencial no tendrá un límite bien definido.
La continuidad no es suficiente[editar]

La relación no funciona a la inversa: el que una función sea continua no garantiza su derivabilidad. Es posible que los límites laterales sean iguales pero las derivadas laterales no; en este caso concreto, la función presenta un punto anguloso en dicho punto.
Un ejemplo es la función valor absoluto , que se define como
Esta función es continua en el punto : en este punto la función toma el valor 0, y para valores de infinitamente cercanos a 0, tanto positivos como negativos, el valor de la función tiende a 0. Sin embargo, no es derivable: la derivada lateral por la derecha de es igual a 1, mientras que por la izquierda la derivada lateral vale -1. Como las derivadas laterales dan resultados diferentes, no existe derivada en , a pesar de que la función sea continua en dicho punto.
De manera informal, si el gráfico de la función tiene puntas agudas, se interrumpe o tiene saltos, no es derivable. Sin embargo, la función f(x)=x|x| es diferenciable para todo x.
Notación[editar]
Existen diversas formas para nombrar a la derivada. Siendo f una función, se escribe la derivada de la función respecto al valor en varios modos.
Notación de Lagrange[editar]
La notación más simple para diferenciación, en uso actual, se debe a Lagrange, y consiste en denotar la derivada de una función como : se lee «f prima de x». Esta notación se extiende a derivadas de orden superior, dando lugar a («f segunda de x» o «f dos prima de x») para la derivada segunda, y a para la derivada tercera. La derivada cuarta y siguientes se pueden denotar de dos formas:
- con números romanos: ,
- con números entre paréntesis: .
Esta última opción da lugar también a la notación para denotar la derivada n-ésima de .
Notación de Leibniz[editar]
Otra notación común para la diferenciación es debida a Leibniz. Para la función derivada de , se escribe:
También puede encontrarse como , o . Se lee «derivada de ( o de ) con respecto a ». Esta notación tiene la ventaja de sugerir a la derivada de una función con respecto a otra como un cociente de diferenciales.
Con esta notación, se puede escribir la derivada de en el punto de dos modos diferentes:
Si , se puede escribir la derivada como
Las derivadas sucesivas se expresan como
- o
para la enésima derivada de o de respectivamente. Históricamente, esto viene del hecho que, por ejemplo, la tercera derivada es
la cual se puede escribir como
La notación de Leibniz es muy útil, por cuanto permite especificar la variable de diferenciación (en el denominador); lo cual es pertinente en caso de diferenciación parcial. También facilita recordar la regla de la cadena, porque los términos «d» parecen cancelarse simbólicamente:
En la formulación popular del cálculo mediante límites, los términos «d» no pueden cancelarse literalmente, porque por sí mismos son indefinidos; son definidos solamente cuando se usan juntos para expresar una derivada. En análisis no estándar, no obstante, se pueden ver números infinitesimales que se cancelan.
Ciertamente, Leibnitz (sí) consideró la derivada dy/dx como el cociente de dos «infinitésimos» dy y dx, llamados «diferenciales». Estos infinitésimos no eran números sino cantidades más pequeños que cualquier número positivo.[3]
Notación de Newton[editar]
La notación de Newton para la diferenciación respecto al tiempo, era poner un punto arriba del nombre de la función:
y así sucesivamente.
Se lee «punto » o « punto». Actualmente está en desuso en el área de matemáticas puras, sin embargo se sigue usando en áreas de la física como la mecánica, donde otras notaciones de la derivada se pueden confundir con la notación de velocidad relativa. Se usa para definir la derivada temporal de una variable.
Esta notación de Newton se usa principalmente en mecánica, normalmente para derivadas que involucran la variable tiempo, como variable independiente; tales como velocidad y aceleración, y en teoría de ecuaciones diferenciales ordinarias. Usualmente solo se emplea para las primeras y segundas derivadas.
Notación de Euler[editar]
se lee « sub de », y los símbolos D y ∂ deben entenderse como operadores diferenciales.
Cálculo de la derivada[editar]
La derivada de una función, en principio, puede ser calculada a partir de la definición, expresando el cociente de diferencias y calculando su límite. Sin embargo, salvo para unos pocos casos esto puede resultar laborioso. En la práctica existen fórmulas precalculadas para las derivadas de las funciones más simples, mientras que para las funciones más complicadas se utilizan una serie de reglas que permitan reducir el problema al cálculo de la derivada de funciones más sencillas. Por ejemplo, para calcular la derivada de la función bastaría con conocer: la derivada de , la derivada de , y cómo derivar una composición de funciones.
Derivadas de funciones elementales[editar]
La mayor parte de los cálculos de derivadas requieren tomar eventualmente la derivada de algunas funciones comunes. La siguiente tabla incompleta proporciona algunas de las más frecuentes funciones de una variable real usadas y sus derivadas.
| Función | Derivada | |
|---|---|---|
| Función potencia | Función constante | |
| Función identidad | ||
| Potencia de exponente natural: | ||
| Función raíz cuadrada | ||
| Función recíproca | ||
| Caso general: | ||
| Función exponencial | Base : | |
| Caso general: | ||
| Función logarítmica | Logaritmo en base : | [Nota 1] |
| Caso general: | [Nota 1] | |
| Funciones trigonométricas | Función seno: | |
| Función coseno: | ||
| Función tangente: | ||
| Funciones trigonométricas inversas | Función arcoseno: | |
| Función arcocoseno: | ||
| Función arcotangente: | ||
Reglas usuales de derivación[editar]
En muchos casos, el cálculo de límites complicados mediante la aplicación directa del cociente de diferencias de Newton puede ser anulado mediante la aplicación de reglas de diferenciación. Algunas de las reglas más básicas son las siguientes:
- Regla de la constante: si f(x) es constante, entonces
- Regla de la suma:
- , para toda función f y g y todo número real y .
- para toda función f y g. Por extensión, esto significa que la derivada de una constante multiplicada por una función es la constante multiplicada por la derivada de la función. Por ejemplo,
- para toda función f y g para todos aquellos valores tales que g ≠ 0.
- Regla de la cadena: Si , siendo g derivable en x, y h derivable en g(x), entonces[4]
Ejemplo de cálculo[editar]
La derivada de
es
Aquí, el segundo término se calculó usando la regla de la cadena y el tercero usando la regla del producto. La derivadas conocidas de funciones elementales x2, x4, sen(x), ln(x) y exp(x) = ex, así como la constante 7, también fueron usadas.
Diferenciabilidad[editar]
Una función con dominio en un subconjunto de los reales es diferenciable en un punto si su derivada existe en ese punto; una función es diferenciable en un intervalo abierto si es diferenciable en todos los puntos del intervalo.
Si una función es diferenciable en un punto , la función es continua en ese punto. Sin embargo, una función continua en , puede no ser diferenciable en dicho punto (punto crítico). En otras palabras, diferenciabilidad implica continuidad, pero no su recíproco.
La derivada de una función diferenciable puede ser, a su vez, diferenciable. La derivada de una primera derivada se llama derivada segunda. De un modo parecido, la derivada de una derivada segunda es la derivada tercera, y así sucesivamente. Esto también recibe el nombre de derivación sucesiva o derivadas de orden superior.
Generalizaciones del concepto de derivada[editar]
El concepto simple de derivada de una función real de una sola variable ha sido generalizado de varias maneras:
- Para funciones de varias variables:
- Derivada parcial, que se aplica a funciones reales de varias variables.
- Derivada direccional, extiende el concepto de derivada parcial.
- En análisis complejo:
- Función holomorfa, que extiende el concepto de derivada a cierto tipo de funciones de variables complejas.
- En análisis funcional:
- Derivada fraccional, que extiende el concepto de derivada de orden superior a orden r, r no necesita ser necesariamente un número entero como sucede en las derivadas convencionales.
- Derivada funcional, que se aplica a funcionales cuyos argumentos son funciones de un espacio vectorial de dimensión no finita.
- Derivada en el sentido de las distribuciones, extiende el concepto de derivada a funciones generalizadas o distribuciones, así puede definirse la derivada de una función discontinua como una distribución.
- En geometría diferencial:
- La Derivación un concepto de geometría diferencial.
- En teoría de la probabilidad y teoría de la medida:
- Derivada de Malliavin derivada de un proceso estocástico o variable aleatoria que cambia con el tiempo.
- Derivada de Radon-Nikodym usada en teoría de la medida.
- Diferenciabilidad:
- Diferenciablidad, otra generalización posible para funciones de varias variables cuando existen derivadas continuas en todas direcciones es el de:
- Función diferenciable, que se aplica a funciones reales de varias variables que poseen derivadas parciales según cualquiera de las variables (El argumento de una función de varias variables pertenece a un espacio del tipo de dimensión n finita).
- La Diferenciación en el sentido de Fréchet generaliza el concepto de función diferenciable a espacios de Banach de dimensión infinita.
Aplicaciones[editar]
- Derivada parcial, supongamos que estamos sobre un puente y observamos como varía la concentración de peces con el tiempo exactamente. Estamos en una posición fija del espacio, por lo que se trata de una derivada parcial de la concentración con respecto al tiempo manteniendo fijas la posición en la dirección "x", "y" o "z".
- Derivada total con respecto al tiempo, supongamos que nos movemos en una lancha a motor que se mueve en el río en todas direcciones, unas veces en contra de la corriente, otras a través y otras a favor. Al referir la variación de concentración de peces con el tiempo, los números que resultan han de reflejar también el movimiento de la lancha. La variación de la concentración con el tiempo corresponde a la derivada total.
- Derivada substancial con respecto al tiempo, supongamos que vamos en una canoa a la que no se comunica energía, sino que simplemente flota. En este caso, la velocidad del observador es exactamente la misma que la velocidad de la corriente "v". Al referir la variación de la concentración de peces con respecto al tiempo, los números dependen de la velocidad local de la corriente. Esta derivada es una clase especial de derivada total con respecto al tiempo que se denomina <<derivada sustancial>> o, a veces (más lógicamente) derivada siguiendo al movimiento.
Véase también[editar]
- Reglas de derivación
- Tabla de derivadas
- Derivación de funciones trigonométricas
- Criterio de la derivada de mayor orden
- Derivación numérica
- Integral
Referencias[editar]
- ↑ «derivada». RAE.
- ↑ Serge Lang: Introducción al análisis matemático, pág. 55, ISBN 0-201-62907-0
- ↑ Lee, Karel de: Calculus, Editorial Universitaria de Buenos Aires, pág. 61, 1972
- ↑ Serge Lang: Introducción al análisis matemático pág. 56
Bibliografía[editar]
- Apostol, Tom M. (1967). Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra 1 (2ª edición). Wiley. ISBN 978-0-471-00005-1.
- Spivak, Michael (1994). Calculus (3ª edición). Publish or Perish. ISBN 978-0-914098-89-8.
- Stewart, James (2002). Calculus (5ª edición). Brooks Cole. ISBN 978-0-534-39339-7.
Enlaces externos[editar]
 Wikimedia Commons alberga una categoría multimedia sobre derivada.
Wikimedia Commons alberga una categoría multimedia sobre derivada. Wikilibros alberga un libro o manual sobre cálculo diferencial.
Wikilibros alberga un libro o manual sobre cálculo diferencial. Wikilibros alberga un libro o manual sobre cálculo de derivadas.
Wikilibros alberga un libro o manual sobre cálculo de derivadas.- Weisstein, Eric W. «Derivative». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Hazewinkel, Michiel, ed. (2001), «Derivada», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104.
Parte de la información ha sido extraída de la web Derivadas.es fundada por Jesús en 2004









































































































