Derivación numérica
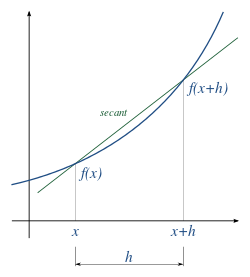
La derivación numérica es una técnica de análisis numérico para calcular una aproximación a la derivada de una función en un punto utilizando los valores y propiedades de la misma.
Formulación mediante diferencias finitas[editar]
Por definición la derivada de una función es:
Las aproximaciones numéricas que podamos hacer (para h > 0) serán:
- Diferencias hacia adelante:
- Diferencias hacia atrás:
La aproximación de la derivada por este método entrega resultados aceptables con un determinado error. Para minimizar los errores se estima que el promedio de ambas entrega la mejor aproximación numérica al problema dado:
- Diferencias centrales:
Véase también[editar]
Enlaces externos[editar]
- Weisstein, Eric W. «Numerical Differentiation». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.






