Movimiento (física)


En física, el movimiento es un cambio de la posición de un cuerpo a lo largo del tiempo respecto de un sistema de referencia.
El estudio del movimiento se puede realizar a través de la cinemática o a través de la dinámica. En función de la elección del sistema de referencia quedarán definidas las ecuaciones del movimiento, ecuaciones que determinarán la posición, la velocidad y la aceleración del cuerpo en cada instante de tiempo. Todo movimiento puede representarse y estudiarse mediante gráficas. Las más habituales son las que representan el espacio, la velocidad o la aceleración en función del tiempo, su medición es mediante kilometraje o metros sobre segundo.
La velocidad y la aceleración siempre son relativas ya que dependen del sistema de referencia elegido para medirlas o calcularlas. Una vez escogido un sistema de referencia y definidas las ecuaciones del movimiento la velocidad y la aceleración del cuerpo en cada instante de tiempo.
Introducción[editar]
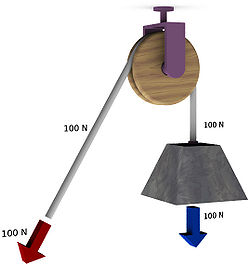
Un sistema físico real se caracteriza por, al menos, tres propiedades importantes:
- Tener una posición en el espacio-tiempo.
- Tener un estado físico definido sujeto a evolución temporal.
- Poderle asociar una magnitud física llamada energía.
El movimiento se refiere al cambio a lo largo del tiempo de una propiedad en el espacio, como puede ser la ubicación, la orientación, la forma geométrica o el tamaño, tal como es medido por un observador físico. Un poco más generalmente el cambio de propiedad en el espacio puede verse influido por las propiedades internas de un cuerpo o sistema físico, o incluso el estudio del movimiento en toda su generalidad lleva a considerar el cambio de dicho estado físico.
La descripción del movimiento de los cuerpos físicos sin considerar las causas que lo originan se denomina cinemática (del griego κινεω, kineo, movimiento) (que solo se ocuparía de las propiedades 1 y 2 anteriores). Se limita al estudio de la trayectoria y el desplazamiento en función de elementos geométricos que evolucionan con el tiempo. Esta disciplina pretende describir el modo en que un determinado cuerpo se mueve. La física clásica nació estudiando la cinemática de cuerpos rígidos.
Posteriormente el estudio de la evolución en el tiempo de un sistema físico en relación con las causas que provocan o conservan el movimiento llevó al desarrollo de la dinámica. Los principios dinámicos más importantes son la inercia, la cantidad de movimiento, la fuerza y la energía mecánica.
La integración de la cinemática y la dinámica desarrolla la disciplina general denominada como mecánica (Griego Μηχανική y de latín mechanica o 'arte de construir máquinas') que es la rama de la física que estudia y analiza el movimiento y reposo de los cuerpos. La mecánica teórica fue durante los siglos XVII, XVIII y principios del siglo XIX, la disciplina de la física que alcanzó mayor abstracción matemática y fue una fuente de mejora del conocimiento científico del mundo. La mecánica aplicada está usualmente relacionada con la ingeniería. Ambos puntos de vista se justifican parcialmente ya que, si bien la mecánica es la base para la mayoría de las ciencias de la ingeniería clásica, no tiene un carácter tan empírico como estas y, en cambio, por su rigor y razonamiento deductivo, se parece más a la matemática. Durante el siglo XX la aparición de nuevos hechos físicos, tanto la consideración de cuerpos físicos moviéndose a velocidades cercanas a la velocidad de la luz como el movimiento de las partículas subatómicas, llevaron a la formulación de teorías más abstractas como la mecánica relativista y la mecánica cuántica que seguían interesándose por la evolución en el tiempo de los sistemas físicos, aunque de una manera más abstracta y general de lo que había hecho la mecánica clásica, cuyo objetivo era básicamente cuantificar el cambio de posición en el espacio de las partículas a lo largo del tiempo y los agentes responsables de dichos cambios.
Características cinemáticas del movimiento[editar]
Móvil[editar]
Se entiende por móvil al objeto en movimiento del que se quiere estudiar tanto su cinemática como su dinámica. De acuerdo al móvil estudiado se pueden identificar diferentes perspectivas del movimiento:
- Móvil puntual: El móvil se reduce a un punto teórico para simplificar su estudio. Desde un punto de vista cinemático, el único tipo de movimiento admisible para un móvil puntual es aquel en el que se observa un cambio de ubicación con respecto a un sistema de coordenadas de referencia, definido como movimiento de traslación.
- Móvil sólido rígido: El móvil es un objeto tridimensional no deformable. El término "rígido" se refiere desde una idealización matemática, a que la distancia entre dos puntos materiales cualesquiera del cuerpo permanece invariable en el transcurso del tiempo.

El movimiento más general de un móvil sólido rígido puede considerarse como la superposición de dos tipos de movimiento básicos:
- - movimiento de traslación, en donde un punto de referencia denominado centro de masas se describe de acuerdo a la simplificación mecánica de un móvil puntual
- - movimiento de rotación, en el que se describe el cambio de orientación del móvil o un sistema de referencia de forma que un punto o una línea (llamada eje de rotación), permanecen fijos.
- Móvil sólido deformable: El móvil es un objeto tridimensional deformable, es decir, existe a lo largo de la evolución temporal un estado tal en el que la distancia entre dos puntos materiales cualesquiera del cuerpo puede variar, lo que se puede evidenciar como un cambio en el tamaño o forma del móvil, denominada deformación. La deformación puede ser:
- -plástica, si el cuerpo no regresa a su forma original después de retirar la carga aplicada o
- -elástica, si el cuerpo regresa a su forma original después de retirar la carga aplicada. Si una deformación elástica genera un movimiento repetitivo alrededor de una posición de equilibrio, se denomina vibración.
El movimiento global de un móvil sólido deformable se descompone en sus movimientos de traslación, rotación y deformación.

- Fluido: El móvil es descrito como un medio continuo sin forma definida, infinitamente deformable, en el cual los desplazamientos que un punto material puede alcanzar en el seno del fluido no están determinados (esto contrasta con los sólidos deformables, donde los desplazamientos están mucho más limitados). Presenta ausencia de memoria de forma, es decir, toma la forma del recipiente que lo contenga, sin que existan fuerzas de recuperación elástica como en los móviles sólidos.
Instante y duración[editar]
El tiempo es una magnitud física con la que medimos la duración o separación de acontecimientos. El tiempo permite ordenar los sucesos en secuencias. Dados dos eventos puntuales E1 y E2, que ocurren respectivamente en dos coordenadas temporales t1 y t2, y en puntos del espacio diferentes P1 y P2, todas las teorías físicas admiten que estos pueden cumplir una y solo una de las siguientes tres condiciones:[1]
- Es posible para un observador estar presente en el evento E1, y luego estar en el evento E2, y en ese caso se afirma que E1 es un evento anterior a E2. Además, si eso sucede, ese observador no podrá verificar E2.
- Es posible para un observador estar presente en el evento E2 y luego estar en el evento E1, y en ese caso se afirma que E1 es un evento posterior a E2. Además si eso sucede, ese observador no podrá verificar E1.
- Es imposible, para un observador puntual, estar presente simultáneamente en los dos eventos E1 y E2.
Para fines de descripción del movimiento, una duración entre las coordenadas temporales t1 y t2 se puede definir como Δt. Si dicha duración es infinitesimal (dt) se denomina como instante.
Posición y desplazamiento[editar]

El espacio físico es el lugar donde se encuentran los entes materiales. El espacio físico es habitualmente concebido con tres dimensiones lineales, aunque los físicos modernos usualmente lo consideran, con el tiempo, como una parte de un infinito continuo de cuatro dimensiones conocido como espacio-tiempo, que en presencia de materia es curvo. La posición de un móvil se define como la variable de estado que proporciona una descripción geométrica definida en un instante dt determinado con respecto a un lugar geométrico descrito por el espectador. Así, se puede utilizar un sistema de coordenadas ortogonales, cilíndricas o esféricas para describir la posición de un cuerpo.
El desplazamiento es el vector que define la posición de un punto o partícula en relación con un origen A con respecto a una posición B. El vector se extiende desde el punto de referencia hasta la posición final. Cuando se habla del desplazamiento en el espacio solo importa la posición inicial y la posición final, ya que la trayectoria que se describe no es de importancia.
Trayectoria[editar]


La trayectoria es el lugar geométrico de las posiciones sucesivas por las que pasa un cuerpo en su movimiento. La trayectoria depende del sistema de referencia en el que se describa el movimiento, con respecto al tipo de móvil y el punto de vista del observador. La trayectoria de un movimiento de traslación se define por la ecuación parametrizada de la curva descrita en el espacio geométrico por un móvil puntual o el centro de masas de un móvil sólido . Las trayectorias de una rotación se describen en función a los ángulos de Euler y de superficies de revolución. La trayectoria de una deformación se describe mediante las medidas geométricas de deformación. Para fluidos en movimiento, el análogo a la trayectoria es el tipo de flujo: un flujo laminar es el movimiento de un fluido cuando este es ordenado, estratificado, suave. En un flujo laminar el fluido se mueve en láminas paralelas sin entremezclarse y cada partícula de fluido sigue una trayectoria suave, llamada línea de corriente. Se llama flujo turbulento al movimiento de un fluido que se da en forma caótica, en que las partículas se mueven desordenadamente y las trayectorias de las partículas se encuentran formando pequeños remolinos periódicos, (no coordinados).
Velocidad y rapidez[editar]

De manera genérica, una rapidez o velocidad se define como la tasa de variación de una determinada magnitud física con respecto al tiempo. En el caso de movimientos traslacionales, la velocidad es una magnitud física de carácter vectorial que expresa el desplazamiento de un objeto por unidad de tiempo.
En el lenguaje cotidiano se emplea las palabras rapidez y velocidad de manera indistinta. En física se hace una distinción entre ellas. De manera muy sencilla, la diferencia es que la velocidad es la rapidez en una dirección determinada. Cuando se dice que un auto viaja a 60 km/h se está indicando su rapidez. Pero al decir que un auto se desplaza a 60 km/h hacia el norte se está especificando su velocidad. La rapidez describe qué tan aprisa se desplaza un objeto; la velocidad describe que tan aprisa lo hace y en que dirección.
La velocidad de movimiento en un instante dado depende del observador tanto en mecánica clásica como en teoría de la relatividad. En mecánica cuántica la velocidad de un móvil al igual que su trayectoria no tiene porqué estar definida en un instante dado, de acuerdo con algunas interpretaciones de la teoría. El fenómeno del Zitterbewegung sugiere que un electrón podría tener un movimiento oscilatorio transversal alrededor de lo que su "trayectoria" clásica (es decir, el camino que debería seguir si la descripción clásica fuera correcta).
La rapidez o también llamada celeridad es la relación entre la distancia recorrida y el tiempo empleado en recorrerla. Un auto, por ejemplo, recorre un cierto número de kilómetros en una hora que puede ser de 110km/h. La rapidez es una medida de que tan veloz se mueve un objeto. Es la razón de cambio a la que se recorre la distancia, ya que la expresión razón de cambio indica que estamos dividiendo alguna cantidad entre el tiempo, por lo tanto, la rapidez se mide siempre en términos de una unidad de distancia dividida entre una unidad de tiempo.
En movimientos rotacionales, se define la velocidad angular como la tasa de variación entre el ángulo girado por una unidad de tiempo y se designa mediante la letra griega ω. Su unidad en el Sistema Internacional es el radián por segundo (rad/s). Se emplea como una medida de la velocidad de rotación.
La velocidad de deformación es una magnitud que mide el cambio de deformación respecto al tiempo. Para problemas uniaxiales es simplemente la derivada temporal de la deformación longitudinal, mientras que para problemas o situaciones tridimensionales se representa por un tensor de segundo rango. En movimientos periódicos se emplea adicionalmente la frecuencia, la cual es una magnitud que mide el número de repeticiones por unidad de tiempo de cualquier fenómeno o suceso periódico, tales como rotaciones, oscilaciones y vibraciones. Su unidad es el Herzio.
En el movimiento de un fluido, el flujo volumétrico es una variable cinématica que se define como el volumen de fluido que pasa por una superficie dada en un tiempo determinado. Dada un área A, sobre la cual fluye un fluido con un ángulo desde la dirección perpendicular a A con un flujo volumétrico Q, se puede definir la velocidad de flujo como:
Aceleración[editar]
En física el término aceleración es una magnitud vectorial que se aplica tanto a los aumentos como a las disminuciones de rapidez en una unidad de tiempo. El término aceleración se aplica tanto a cambios de rapidez como a cambios de dirección.
En movimientos de traslación, el vector velocidad v es tangente a la trayectoria, mientras que el vector aceleración a puede descomponerse en dos componentes (llamadas componentes intrínsecas) mutuamente perpendiculares: una componente tangencial at (en la dirección de la tangente a la trayectoria), llamada aceleración tangencial, y una componente normal an (en la dirección de la normal principal a la trayectoria), llamada aceleración normal o centrípeta (este último nombre en razón a que siempre está dirigida hacia el centro de curvatura).

Si se recorre una curva con una rapidez constante de 50 km/h, se sentirán los efectos de la aceleración como una tendencia a inclinarse hacia el exterior de la curva (inercia). Se puede recorrer la curva con rapidez constante, pero la velocidad no es constante ya que la dirección cambia a cada instante, por lo tanto, el estado de movimiento cambia, es decir, se está acelerando. Por ejemplo, los frenos de un auto pueden producir grandes aceleraciones retardantes, es decir, pueden producir un gran decremento por segundo de su rapidez. A esto se le suele llamar desaceleración o aceleración negativa.
La aceleración normal es una medida de la curvatura de la trayectoria, diferentes observadores en movimiento no uniforme respecto a ellos observarán fuerzas y aceleraciones diferentes y por tanto trayectorias diferentes. Si un observador inercial examina la trayectoria de una partícula que se mueve en línea recta y con velocidad uniforme (trayectoria de curvatura cero), cualquier otro observador inercial verá la partícula moverse en línea recta y con velocidad uniforme (aunque no la misma recta), en el caso de observadores arbitrarios en movimiento acelerado entre ellos las formas de las trayectorias pueden diferir notablemente, ya que al medir los dos observadores aceleraciones completamente diferentes, la trayectoria de la partícula se curvará de maneras muy diferentes para uno y otro observador.
En movimientos rotacionales, se emplea el concepto de aceleración angular a la tasa de variación entre la velocidad angular con respecto al tiempo.

Características dinámicas del movimiento[editar]
Todas las teorías físicas del movimiento atribuyen al movimiento una serie de características o atributos dinámicos como:
- Inercia.
- La cantidad de movimiento
- El sistema de fuerzas ejercidos sobre el móvil
- La energía mecánica
En mecánica clásica y mecánica relativista todos ellos son valores numéricos medibles, mientras que en mecánica cuántica esas magnitudes son en general variables aleatorias para las que es posible predecir sus valores medios, pero no el valor exacto en todo momento.
Inercia[editar]
En física, la inercia (del latín inertĭa) es la propiedad que tienen los cuerpos de permanecer en su estado de reposo relativo o movimiento relativo. Dicho de forma general, es la resistencia que opone la materia al modificar su estado de movimiento, incluyendo cambios en la velocidad o en la dirección del movimiento. Como consecuencia, un cuerpo conserva su estado de reposo relativo o movimiento rectilíneo uniforme relativo si no hay una fuerza que, actuando sobre él, logre cambiar su estado de movimiento.
En movimientos de traslación, la medida de inercia lo proporciona la masa. En un móvil puntual se asume que toda la masa se concentra en el punto que describe al móvil, mientras que en móviles sólidos se puede simplificar su traslación describiendo a un punto denominado Centro de masas de manera análoga a un móvil puntual.
En movimientos de rotación, el momento de inercia rotacional (símbolo I) es una medida de resistencia a la rotación de un cuerpo que refleja la distribución de masa de un cuerpo respecto a un eje de giro. El momento de inercia únicamente depende de la geometría del cuerpo y de la posición del eje de giro.

Por otro lado, las medidas de resistencia a la deformación son representadas principalmente por las medidas de rigidez, como por ejemplo la constante de Hooke.
En el movimiento de un fluido, la inercia de un flujo está representada tanto por su densidad como por su viscosidad, su rozamiento con el recipiente y su adhesión a las paredes.
Cantidad de movimiento (momentum)[editar]
La cantidad de movimiento, momento lineal, ímpetu o momentum es una magnitud física fundamental de tipo vectorial que describe el movimiento de un cuerpo en cualquier teoría mecánica definida como el producto de una unidad de inercia y una tasa de variación espacial con respecto al tiempo dado un instante determinado.
De acuerdo al concepto de la cantidad de movimiento, se define como reposo mecánico al estado mecánico en el que para cualquier instante dado, cualquier medida de cantidad de movimiento es igual a cero.
De acuerdo al concepto de la cantidad de movimiento, se define como movimiento uniforme aquel en donde la cantidad de movimiento permanece constante a lo largo del tiempo.
Se denomina impulso a la magnitud vectorial definida como la variación en la cantidad de movimiento que experimenta un objeto físico en un sistema cerrado.

En movimientos de traslación de un solo móvil, se define la cantidad de movimiento lineal (o momento lineal) como el producto de la masa con su velocidad lineal. La idea intuitiva tras esta definición está en que la "cantidad de movimiento" dependía tanto de la masa como de la velocidad: si se imagina una mosca y un camión, ambos moviéndose a 40 km/h, la experiencia cotidiana dice que la mosca es fácil de detener con la mano mientras que el camión no, aunque los dos vayan a la misma velocidad. Esta intuición llevó a definir una magnitud que fuera proporcional tanto a la masa del objeto móvil como a su velocidad.
En movimientos de rotación, el momento angular o momento cinético es una magnitud física que se relaciona con el producto vectorial entre el momento de inercia y la velocidad angular. Esta magnitud desempeña respecto a las rotaciones un papel análogo al momento lineal en las traslaciones. El momento angular para un cuerpo rígido que rota respecto a un eje es la resistencia que ofrece dicho cuerpo a la variación de la velocidad angular. Sin embargo, eso no implica que sea una magnitud exclusiva de las rotaciones; por ejemplo, el momento angular de una partícula que se mueve libremente con velocidad constante (en módulo y dirección) también se conserva.
Si estamos interesados en averiguar la cantidad de movimiento de, por ejemplo, un fluido que se mueve según un campo de velocidades es necesario sumar la cantidad de movimiento de cada partícula del fluido, es decir, de cada diferencial de masa o elemento infinitesimal:
En movimientos de fluidos, la conservación del momento lineal de un fluido en movimiento se encuentra generalizado por las ecuaciones de Navier-Stokes.
Fuerza[editar]
En física, la fuerza es una magnitud física que mide la tasa de variación del intercambio de cantidad de movimiento entre dos móviles con respecto a la duración de dicho intercambio. Según una definición clásica, fuerza es todo agente capaz de modificar la cantidad de movimiento o la forma de los cuerpos materiales. En el Sistema Internacional de Unidades, la fuerza se mide en "Newtons (N)".
Cuando varias fuerzas actúan sobre un solo móvil, todas se sumarán vectorialmente para constituir una sola fuerza denominada fuerza resultante. En movimientos de traslación de móviles puntuales o sólidos, cuando la fuerza resultante es cero y la cantidad de movimiento es cero, se observará equilibrio mecánico a manera de reposo. Cuando la fuerza resultante es cero y la cantidad de movimiento es constante con valor distinto a cero, se observará un movimiento rectilíneo uniforme. Si la fuerza resultante es distinta a cero, ésta será equivalente al producto de la masa instantánea por la aceleración instantánea. En términos de cantidad de movimiento, se aplicó un impulso. Esto es enunciado en la primera y segunda leyes de Newton. Los movimientos de traslación curvilíneos implican la aplicación de un fuerza normal denominada fuerza centrípeta.
En los movimientos rotacionales, el análogo a la fuerza se denomina como momento de una fuerza (respecto a un punto dado) o torque a una magnitud obtenida como producto vectorial del vector de posición del punto de aplicación de la fuerza (con respecto al punto al cual se toma el momento) por el vector fuerza, en ese orden. Así, la suma de todos los torques en un sistema rotatorio conllevará a un torque resultante. Si el torque resultante es cero con momento angular cero, el cuerpo no presentará rotación. Si el torque resultante es cero con momento angular constante diferente de cero, se observará una rotación uniforme o un movimiento circular uniforme. Si el torque resultante es distinto a cero, se apreciará una aceleración angular neta y por lo tanto se cambiará el estado de rotación. Las ecuaciones de Euler describen el movimiento de un sólido rígido en rotación en un sistema de referencia con el sólido.
En deformaciones, el análogo a las fuerzas son los esfuerzos mecánicos, las tensiones mecánicas y las torsiones mecánicas. La dinámica de las deformaciones se describe por:
- -ecuaciones de equilibrio, que relacionan tensiones internas del sólido con las cargas aplicadas. Esta parte es análoga a la primera Ley de Newton.
- -ecuaciones constitutivas, que relacionan tensión y deformación. La más representativa es la ecuación de Hooke. En las ecuaciones constitutivas pueden intervenir también otras magnitudes como temperatura, velocidad de deformación, deformaciones plásticas acumuladas, variables de endurecimiento, etc. Esta parte es análoga a la segunda ley de Newton.
- -ecuaciones de compatibilidad, a partir de la cual pueden calcularse los desplazamientos en función de las deformaciones y las condiciones de contorno o enlace con el exterior.
En mecánica de fluidos, el equivalente a la fuerza es la presión. En un fluido puede haber los siguientes tipos de presión:
- - La presión hidrostática, debida al efecto gravitatorio de un fluido en reposo. El teorema de Torricelli enuncia que la velocidad de un líquido en una vasija abierta, por un orificio, es la que tendría un cuerpo cualquiera, cayendo libremente en el vacío desde el nivel del líquido hasta el centro de gravedad del orificio y explica el flujo de un líquido contenido en un recipiente, a través de un pequeño orificio, bajo la acción de la presión hidrostática.
- - La presión externa en la que se aplica un factor de fuerza extrínseca al fluido, como puede ser un émbolo o un objeto caído. El efecto de la presión externa en un fluido incompresible se explica por el principio de Pascal mientras que el efecto de la presión externa en un fluido compresible se explica con la ley de Boyle. La tensión superficial es la tensión que actúa tangencialmente por unidad de longitud en el borde de una superficie libre de un líquido en equilibrio y que tiende a contraer dicha superficie. Las fuerzas cohesivas entre las moléculas de un líquido son las responsables del fenómeno conocido como tensión superficial y presentan resistencia a la penetración de la superficie del fluido incompresible.
- - La presión hidrodinámica es aquella dependiente de la dirección considerada alrededor de un punto de acuerdo al estado de movimiento del mismo. La viscosidad dinámica, es una magnitud que relaciona el esfuerzo o tensión local en un fluido en movimiento con la velocidad de deformación de las partículas fluidas. La viscosidad de un fluido es la resistencia a que las distintas láminas deslicen entre sí. Los fluidos newtonianos son aquellos cuya viscosidad dinámica puede considerarse constante y por lo tanto a ciertos valores de velocidad presentan flujos laminares. El efecto Venturi consiste en un fenómeno en el que un fluido newtoniano en flujo laminar dentro de un conducto cerrado disminuye su presión cuando aumenta la velocidad al pasar por una zona de sección menor. En un fluido en movimiento general, al medir la presión según diferentes direcciones alrededor de un punto, esta no será constante, dependiendo la dirección donde la presión es máxima y mínima, y de la dirección y valor de la velocidad en ese punto.

Energía[editar]
En física, la energía se define como la capacidad para realizar una transformación en un sistema físico, por ejemplo, al elevar un objeto, transportarlo (movimiento), deformarlo o calentarlo. La energía no es un estado físico real, ni una "sustancia intangible" sino una magnitud escalar que se le asigna al estado del sistema físico, es decir, la energía es una herramienta o abstracción matemática de una propiedad de los sistemas físicos. Por ejemplo, se puede decir que un sistema con energía cinética nula está en reposo. La energía se mide con la unidad "joule (J)".
De esta manera, a todo movimiento en un instante específico se le asigna una cantidad de energía asociada cinemáticamente a su velocidad y dinámicamente a su cantidad de movimiento. A dicha magnitud se le nombra energía cinética.
Para cualquier movimiento de traslación, su energía cinética instantánea se define como función de la mitad de la masa y el cuadrado de la magnitud de la velocidad lineal instantánea: . Así, un cuerpo en reposo tiene energía cinética instantánea igual a cero. En un movimiento rectilíneo uniforme, la energía cinética es constante para cualquier instante dado.

El trabajo que realiza una fuerza se define como el producto de esta por el camino que recorre su punto de aplicación y por el coseno del ángulo que forman el uno con el otro.[2] El trabajo es una magnitud física escalar que se representa con la letra (del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.
Matemáticamente, el trabajo para una partícula que se desplaza a lo largo de una curva C se expresa como:
Para el caso de una fuerza constante la ecuación anterior se reduce a:
Donde es el trabajo mecánico, es la magnitud de la fuerza, es el desplazamiento y es el ángulo que forman entre sí el vector fuerza y el vector desplazamiento (véase dibujo).
Cuando el vector fuerza es perpendicular al vector desplazamiento del cuerpo sobre el que se aplica, dicha fuerza no realiza trabajo alguno. Asimismo, si no hay desplazamiento, el trabajo también será nulo.
Para cualquier movimiento de rotación, la energía cinética rotacional se describe como función de la mitad del momento de inercia rotacional y el cuadrado de la magnitud de la velocidad angular instantánea: . Así, una rotación en movimiento circular uniforme presenta un valor constante de energía cinética rotacional.
Para movimientos armónicos y cualquier tipo de deformaciones, se puede describir la energía cinética como consecuencia de las fuerzas involucradas son centrales y, por tanto, conservativas. En consecuencia, se puede definir un campo escalar llamado energía potencial (Ep) asociado a la fuerza. Para hallar la expresión de la energía potencial, basta con integrar la expresión de la fuerza (esto es extensible a todas las fuerzas conservativas) y cambiarla de signo, obteniéndose:
(15)
La energía potencial alcanza su máximo en los extremos de la trayectoria y tiene valor nulo (cero) en el punto x = 0, es decir el punto de equilibrio.
La energía cinética cambiará a lo largo de las oscilaciones pues lo hace la velocidad:
(16)
La energía cinética es nula en -A o +A (v=0) y el valor máximo se alcanza en el punto de equilibrio (máxima velocidad Aω).
(17)
En el caso de los fluidos, el principio de Bernoulli establece que la energía total de un fluido en cualquier momento consta de tres componentes:
- cinética: es la energía debida a la velocidad que posea el fluido;
- potencial o gravitacional: es la energía debido a la altitud que un fluido posea;
- energía de presión: es la energía que un fluido contiene debido a la presión que posee.
Una forma de representar la ecuación del principio de Bernoulli se expresa como la suma de la energía cinética, la energía de flujo y la energía potencial gravitatoria por unidad de masa:
En una línea de corriente cada tipo de energía puede subir o disminuir en virtud de la disminución o el aumento de las otras dos. Pese a que el principio de Bernoulli puede ser visto como otra forma de la ley de la conservación de la energía realmente se deriva de la conservación de la Cantidad de movimiento.
Historia del concepto físico de movimiento[editar]
Las cuestiones acerca de las causas del movimiento surgieron en la mente del hombre hace más de 25 siglos, pero las respuestas que hoy conocemos no se desarrollaron hasta los tiempos de Galileo Galilei (1564–1642) e Isaac Newton (1642–1727).
Estudios del movimiento en la época clásica[editar]
- Anaximandro pensaba que la naturaleza procedía de la separación, por medio de un eterno movimiento, de los elementos opuestos (por ejemplo, frío-calor), que estaban encerrados en algo llamado materia primordial.
- Demócrito decía que la naturaleza está formada por piezas indivisibles de materia llamadas átomos, y que el movimiento era la principal característica de estos, siendo el movimiento un cambio de lugar en el espacio.
- Las paradojas de Zenón son una serie de paradojas o aporías ideadas por Zenón de Elea. Dedicado principalmente al problema del continuo y a las relaciones entre espacio, tiempo y movimiento, Zenón habría planteado — según señala Proclo — un total de 40 paradojas, de las cuales se han conservado nueve o diez descripciones completas (en la Física[3][4] de Aristóteles y el comentario de Simplicio a esta obra).
- Aristóteles rechaza la tarea de retomar el concepto de átomo, de Democrito, y de la energía, de Aristóteles, definiendo a la energía como indeterminación absoluta de la materia, lo que comprendemos como materia no másica y a los cuerpos como determinación absoluta de la materia, lo que comprendemos como materia másica. Recordemos que Epícuro es el primer físico absoluto, de ahí se dan dos importantes rasgos, que los cuerpos percibidos son materiales y que la energía, que provoca el movimiento en estos, también es material.
La importancia de esta tesis, epicúrea, es inconmensurable en la historia de la física, debido a que resuelve las problemáticas de las tesis expuestas antes de esta, y posteriormente tiene influencia en la física, sobre todo a partir de los siglos XVI y XVII, gracias al redescubrimiento de Poggio Bracciolini y de Pierre Gassendi de las obras de Epícuro. Un ejemplo claro de influencia esta en Newton, que de hecho desvirtuó la teoría, llegando así a errores en su ley de gravitación universal, un error claro es el fundamento que da al movimiento en la gravedad, analógicamente comparado con el determinismo mecanicista de Demócrito. Quienes que confirmaron definitivamente, con sus trabajos, la tesis de Epícuro fueron Max Planck y Albert Einstein, después de veintiún siglos de duda sobre la tesis de Epícuro.
- Lucrecio:para evitar el determinismo mecanicista, ya criticado por Aristóteles, toma el pensamiento de Epicuro e introduce la tesis de que los átomos caen en el vacío y experimentan por sí mismos una declinación que les permite encontrarse. De esta forma se trata de imponer un cierto orden a la idea original que suponía que las cosas se formaban con un movimiento caótico de átomos.
- El gran filósofo griego Aristóteles (384 a. C.-322 a. C.) propuso explicaciones sobre lo que ocurría en la naturaleza, considerando las observaciones que hacía de las experiencias cotidianas y su razonamiento, aunque no se preocupaba por comprobar sus afirmaciones.
Aristóteles formuló su teoría sobre la caída de los cuerpos afirmando que los más pesados caían más rápido que los más ligeros, es decir entre más peso tengan los cuerpos más rápido caen. Esta teoría fue aceptada por casi dos mil años hasta que en el siglo XVII Galileo realiza un estudio más cuidadoso sobre el movimiento de los cuerpos y su caída, sobre la cual afirmaba: "cualquier velocidad, una vez impartida a un cuerpo se mantendrá constantemente, en tanto no existan causas de aceleración o retardamiento, fenómeno que se observará en planos horizontales donde la fricción se haya reducido al mínimo" Esta afirmación lleva consigo el principio de la inercia de Galileo la cual brevemente dice: «Si no se ejerce ninguna fuerza sobre un cuerpo, este permanecerá en reposo o se moverá en línea recta con velocidad constante».
Él fue estudiando los movimientos de diversos objetos en un plano inclinado y observó que en el caso de planos con pendiente descendente hay una causa de aceleración, mientras que en los planos con pendiente ascendente hay una causa de retardamiento. De esta experiencia razonó que cuando las pendientes de los planos no son descendentes ni ascendentes no debe haber aceleración ni retardamiento por lo que llegó a la conclusión de que cuando el movimiento es a lo largo de un plano horizontal debe ser permanente. Galileo hizo un estudio para comprobar lo que había dicho Aristóteles acerca de la caída de los cuerpos, para hacerlo se subió a lo más alto de la torre de Pisa y soltó dos objetos de distinto peso; y observó que los cuerpos caen a la misma velocidad sin importar su peso, quedando así descartada la teoría de la caída de los cuerpos de Aristóteles.
Movimiento de acuerdo a la Mecánica Clásica[editar]
La mecánica clásica es una formulación de la mecánica para describir mediante leyes el comportamiento de cuerpos físicos macroscópicos en reposo y a velocidades pequeñas comparadas con la velocidad de la luz. A partir de Galileo, los hombres de ciencia comenzaron a desarrollar técnicas de análisis que permitían una descripción cuantificable del fenómeno.
En mecánica clásica, la trayectoria es el lugar geométrico de las posiciones sucesivas por las que pasa un cuerpo en su movimiento. La trayectoria depende del sistema de referencia en el que se describa el movimiento; es decir, el punto de vista del observador. La descripción del movimiento de partículas puntuales o corpúsculos (cuya estructura interna no se requiere para describir la posición general de la partícula) es similar en mecánica clásica y mecánica relativista. En ambas, la trayectoria del movimiento es una curva parametrizada por un parámetro escalar. En la descripción de la mecánica clásica el parámetro es el tiempo universal, mientras que en relatividad se usa el intervalo relativista ya que el tiempo propio percibido por la partícula y el tiempo medido por diferentes observadores no coincide.
En mecánica clásica es perfectamente posible definir unívocamente la longitud Lc de la trayectoria o camino recorrido por un cuerpo. También puede definirse sin ambigüedad la distancia d que hay entre un punto inicial y el final de su trayectoria; está representado por la longitud de la línea recta que une el punto inicial con el punto final. Ambas magnitudes están relacionadas por la desigualdad siguiente:
Existen varias formulaciones diferentes, de la mecánica clásica para describir un mismo fenómeno natural, que independientemente de los aspectos formales y metodológicos que utilizan llegan a la misma conclusión.
- La mecánica vectorial, deviene directamente de las leyes de Newton, por eso también se le conoce con el gentilicio de newtoniana. Es aplicable a cuerpos que se mueven en relación con un observador a velocidades pequeñas comparadas con la de la luz. Fue construida en un principio para una sola partícula moviéndose en un campo gravitatorio. Se basa en el tratamiento de dos magnitudes vectoriales bajo una relación causal: la fuerza y la acción de la fuerza, medida por la variación del momentum (cantidad de movimiento). El análisis y síntesis de fuerzas y momentos constituye el método básico de la mecánica vectorial. Requiere del uso privilegiado de sistemas de referencia inercial.
- La mecánica analítica (analítica en el sentido matemático de la palabra y no filosófico). Sus métodos son poderosos y trascienden de la Mecánica a otros campos de la física. Se puede encontrar el germen de la mecánica analítica en la obra de Leibniz que propone para solucionar los problemas mecánicos otras magnitudes básicas (menos oscuras según Leibniz que la fuerza y el momento de Newton), pero ahora escalares, que son: la energía cinética y el trabajo. Estas magnitudes están relacionadas de forma diferencial. La característica esencial es que, en la formulación, se toman como fundamentos primeros principios generales (diferenciales e integrales), y que a partir de estos principios se obtengan analíticamente las ecuaciones de movimiento.
La cinemática clásica trata del estudio del movimiento de los cuerpos en general, y, en particular, el caso simplificado del movimiento de un punto material. Para sistemas de muchas partículas, tales como los fluidos, las leyes de movimiento se estudian en la mecánica de fluidos. El movimiento trazado por una partícula lo mide un observador respecto a un sistema de referencia. Desde el punto de vista matemático, la Cinemática expresa cómo varían las coordenadas de posición de la partícula (o partículas) en función del tiempo. La función que describe la trayectoria recorrida por el cuerpo (o partícula) depende de la velocidad (la rapidez con la que cambia de posición un móvil) y de la aceleración (variación de la velocidad respecto del tiempo).
El movimiento de una partícula (o cuerpo rígido) se puede describir según los valores de velocidad y aceleración, que son magnitudes vectoriales.
- Si la aceleración es nula, da lugar a un movimiento rectilíneo uniforme y la velocidad permanece constante a lo largo del tiempo.
- Si la aceleración es constante con igual dirección que la velocidad, da lugar al movimiento rectilíneo uniformemente acelerado y la velocidad variará a lo largo del tiempo.
- Si la aceleración es constante con dirección perpendicular a la velocidad, da lugar al movimiento circular uniforme, donde el módulo de la velocidad es constante, cambiando su dirección con el tiempo.
- Cuando la aceleración es constante y está en el mismo plano que la velocidad y la trayectoria, tenemos el caso del movimiento parabólico, donde la componente de la velocidad en la dirección de la aceleración se comporta como un movimiento rectilíneo uniformemente acelerado, y la componente perpendicular se comporta como un movimiento rectilíneo uniforme, generándose una trayectoria parabólica al componer ambas.
- Cuando la aceleración es constante pero no está en el mismo plano que la velocidad y la trayectoria, se observa el efecto de Coriolis.
- En el movimiento armónico simple se tiene un movimiento periódico de vaivén, como el del péndulo, en el cual un cuerpo oscila a un lado y a otro desde la posición de equilibrio en una dirección determinada y en intervalos iguales de tiempo. La aceleración y la velocidad son funciones, en este caso, sinusoidales del tiempo.
Al considerar el movimiento de traslación de un cuerpo extenso, en el caso de ser rígido, conociendo como se mueve una de las partículas, se deduce como se mueven las demás. Así basta describir el movimiento de una partícula puntual tal como el centro de masa del cuerpo para especificar el movimiento de todo el cuerpo. En la descripción del movimiento de rotación hay que considerar el eje de rotación respecto del cual rota el cuerpo y la distribución de partículas respecto al eje de giro. El estudio del movimiento de rotación de un sólido rígido suele incluirse en la temática de la mecánica del sólido rígido por ser más complicado. Un movimiento interesante es el de una peonza, que al girar puede tener un movimiento de precesión y de nutación
Cuando un cuerpo posee varios movimientos simultáneamente, tal como uno de traslación y otro de rotación, se puede estudiar cada uno por separado en el sistema de referencia que sea apropiado para cada uno, y luego, superponer los movimientos.
En mecánica newtoniana el movimiento de una partícula en el espacio tridimensional se representa por una función vectorial:
El conjunto imagen se denomina trayectoria y se obtiene integrando la ecuación diferencial anterior con las condiciones de contorno adecuadas. Dado que la ecuación diferencial puede ser complicada a veces se buscan integrales de movimiento que permitan encontrar la trayectoria más fácilmente. Para un sistema de n partículas libres que ejercen acciones a distancia instáneas la idea anterior se generaliza:
Si existen ligaduras en el movimiento puede resultar más sencillo y económico pasar a un sistema de coordenadas generalizadas y trabajar con una formulación abstracta típica de la mecánica analítica.

Una ley de movimiento es una relación cuantitiva entre variables necesarias para describir el movimiento de los cuerpos. Históricamente la mecánica clásica surgió tras la formulación por parte de Isaac Newton de tres "leyes" cuantitativas que describían el movimiento de una partícula material.
Las Leyes de Newton, también conocidas como Leyes del movimiento de Newton, son tres principios a partir de los cuales se explican la mayor parte de los problemas planteados por la dinámica, en particular aquellos relativos al movimiento de los cuerpos. Revolucionaron los conceptos básicos de la física y el movimiento de los cuerpos en el universo.
En tanto que constituyen los cimientos no solo de la dinámica clásica sino también de la física clásica en general. Aunque incluyen ciertas definiciones y en cierto sentido pueden verse como axiomas, Newton afirmó que estaban basadas en observaciones y experimentos cuantitativos; ciertamente no pueden derivarse a partir de otras relaciones más básicas. La demostración de su validez radica en sus predicciones y la validez de esas predicciones fue verificada en todos y cada uno de los casos durante más de dos siglos.
Los estudios que el realizó se pueden definir con las siguientes tres leyes que postuló:
- La primera ley del movimiento rebate la idea aristotélica de que un cuerpo solo puede mantenerse en movimiento si se le aplica una fuerza. Newton expone que:
Todo cuerpo permanece en su estado inicial de reposo o movimiento uniforme rectilíneo a menos que sobre él se ejerza una fuerza exterior no equilibrada.
- El ser la primera de las tres leyes de Newton suele inducir a un error muy común atribuyendo el descubrimiento de esta propiedad al propio Newton cuando, en realidad, fue Galileo Galilei en el siglo XVI el primero en observar, estudiar y formalizar dicha propiedad y posteriormente, ya en el siglo XVII, fue tomada por Newton. Esta ley postula, por tanto, que un cuerpo no puede cambiar por sí solo su estado inicial, ya sea en reposo o en movimiento rectilíneo uniforme, a menos que se aplique una fuerza o una serie de fuerzas cuyo resultante no sea nulo sobre él. Newton toma en cuenta, así, el que los cuerpos en movimiento están sometidos constantemente a fuerzas de roce o fricción, que los frena de forma progresiva, algo novedoso respecto de concepciones anteriores que entendían que el movimiento o la detención de un cuerpo se debía exclusivamente a si se ejercía sobre ellos una fuerza, pero nunca entendiendo como esta a la fricción.
- La segunda ley del movimiento de Newton afirma que:
El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.
- Esta ley explica qué ocurre si sobre un cuerpo en movimiento (cuya masa no tiene por qué ser constante) actúa una fuerza neta: la fuerza modificará el estado de movimiento, cambiando la velocidad en módulo o dirección. En concreto, los cambios experimentados en la cantidad de movimiento de un cuerpo son proporcionales a la fuerza motriz y se desarrollan en la dirección de esta; esto es, las fuerzas son causas que producen aceleraciones en los cuerpos. A diferencia de la primera ley de Newton que es descriptiva, la segunda ley también conocida como ley del movimiento permite calcular cuantitativamente las fuerzas, las masas y aceleraciones de los cuerpos.
- Donde:
- F, fuerza que se mide en Newton (N)
- m, masa que se mide en kilogramos o gramos (kg, g)
- a, aceleración que se mide en metros sobre segundos al cuadrado (m/s2)
Nota: hay que tomar en cuenta que 1 N= kg m/s2
- La Tercera ley de Newton afirma que:
Con toda acción ocurre siempre una reacción igual y contraria: o sea, las acciones mutuas de dos cuerpos siempre son iguales y de dirección contraria.
- La tercera ley es completamente original de Newton (pues las dos primeras ya habían sido propuestas de otras maneras por Galileo, Hooke y Huygens) y hace de las leyes de la mecánica un conjunto lógico y completo. Expone que por cada fuerza que actúa sobre un cuerpo, este realiza una fuerza de igual intensidad, pero de dirección contraria sobre el cuerpo que la produjo. Dicho de otra forma, las fuerzas, situadas sobre la misma recta, siempre se presentan en pares de igual magnitud y opuestas en dirección. Es importante observar que este principio de acción y reacción relaciona dos fuerzas que no están aplicadas al mismo cuerpo, produciendo en ellos aceleraciones diferentes, según sean sus masas.
Por lo demás, cada una de esas fuerzas obedece por separado a la segunda ley. Junto con las anteriores leyes, esta permite enunciar los principios de conservación del momento lineal y del momento angular.
Ecuaciones de movimiento en mecánica clásica[editar]
Históricamente el primer ejemplo de ecuación del movimiento que se introdujo en física fue la segunda ley de Newton para sistemas físicos compuestos de agregados partículas materiales puntuales. En estos sistemas el estado dinámico de un sistema quedaba fijado por la posición y velocidad de todas las partículas en un instante dado. Hacia finales del siglo XVIII se introdujo la mecánica analítica o racional, como generalización de las leyes de Newton aplicables a sistemas de referencia inerciales. Se concibieron dos enfoques básicamente equivalentes conocidos como mecánica lagrangiana y mecánica hamiltoniana, que pueden llegar a un elevado grado de abstracción y formalización. Los ejemplos clásicos de ecuación del movimiento más conocidos son:
- La segunda ley de Newton que se usa en mecánica newtoniana:
- Las ecuaciones de Euler-Lagrange que aparecen en mecánica lagrangiana:
- Las ecuaciones de Hamilton que aparecen en mecánica hamiltoniana:
Históricamente el concepto de cantidad de movimiento surgió en el contexto de la mecánica newtoniana en estrecha relación con el concepto de velocidad y el de masa. En mecánica newtoniana se define la cantidad de movimiento lineal como el producto de la masa por la velocidad:
La idea intuitiva tras esta definición está en que la "cantidad de movimiento" dependía tanto de la masa como de la velocidad: si se imagina una mosca y un camión, ambos moviéndose a 40 km/h, la experiencia cotidiana dice que la mosca es fácil de detener con la mano mientras que el camión no, aunque los dos vayan a la misma velocidad. Esta intuición llevó a definir una magnitud que fuera proporcional tanto a la masa del objeto móvil como a su velocidad.
Mecánica lagrangiana y hamiltoniana[editar]
En las formulaciones más abstractas de la mecánica clásica, como la mecánica lagrangiana y la mecánica hamiltoniana, además del momento lineal y del momento angular se pueden definir otros momentos, llamados momentos generalizados o momentos conjugados, asociados a cualquier tipo de coordenada generalizada. Se generaliza así la noción de momento.
Si se tiene un sistema mecánico definido por su lagrangiano L definido en términos de las coordenadas generalizadas (q1,q2,...,qN) y las velocidades generalizadas, entonces el momento conjugado de la coordenada qi viene dado por:
Cuando la coordenada qi es una de las coordenadas de un sistema de coordenadas cartesianas, el momento conjugado coincide con una de las componentes del momento lineal, y, cuando la coordenada generalizada representa una coordenada angular o la medida de un ángulo, el momento conjugado correspondiente resulta ser una de las componentes del momento angular.

Movimiento de acuerdo a la Mecánica relativista[editar]
Para describir la posición de una partícula material, la mecánica relativista hace uso de un sistema de cuatro coordenadas definidas sobre un espacio-tiempo de cuatro dimensiones. El movimiento de una partícula material viene dado por una curva en una 4-variedad lorentziana, cuyo vector tangente es de tipo temporal. Además, las acciones a distancia instantáneas están excluidas ya que al propagarse más rápido que la velocidad de la luz dan lugar a contracciones en el principio de causalidad. Por lo que un sistema de partículas puntuales en interacción debe ser descrito con la ayuda de "campos retardados", es decir, que no actúan de manera instantánea, cuya variación debe determinarse como propagación a partir de la posición de la partícula. Esto complica razonablemente el número de ecuaciones necesarias para describir un conjunto de partículas en interacción.
Otra dificultad añadida es que no existe un tiempo universal para todos los observadores, por lo que relacionar las medidas de diferentes observadores en movimiento relativo es ligeramente más complejo que en la mecánica clásica. Una manera conveniente es definir el intervalo invariante relativista y parametrizar las trayectorias en el espacio-tiempo en función de dicho parámetro. La descripción campos de fuerzas o fluidos requiere definir ciertas magnitudes tensoriales sobre el espacio vectorial tangente al espacio-tiempo.
En mecánica relativista, la trayectoria es el lugar geométrico de las posiciones sucesivas por las que pasa un cuerpo en su movimiento. La trayectoria depende del sistema de referencia en el que se describa el movimiento; es decir, el punto de vista del observador. La descripción del movimiento de partículas puntuales o corpúsculos (cuya estructura interna no se requiere para describir la posición general de la partícula) es similar en mecánica clásica y mecánica relativista. En ambas, la trayectoria del movimiento es una curva parametrizada por un parámetro escalar. En la descripción de la mecánica clásica el parámetro es el tiempo universal, mientras que en relatividad se usa el intervalo relativista ya que el tiempo propio percibido por la partícula y el tiempo medido por diferentes observadores no coincide.
Movimiento de acuerdo a la mecánica cuántica[editar]
La mecánica cuántica[5][6] es una de las ramas principales de la física, y uno de los más grandes avances del siglo XX para el conocimiento humano, que explica el comportamiento de la materia y de la energía. La descripción cuántica del movimiento es más compleja ya que realmente la descripción cuántica del movimiento no asume necesariamente que las partículas sigan una trayectoria de tipo clásico (algunas interpretaciones de la mecánica cuántica sí asumen que exista una trayectoria única, pero otras formulaciones prescinden por completo del concepto de trayectoria), por lo que en esas formulaciones no tiene sentido hablar ni de posición, ni de velocidad.
La aplicación de la mecánica cuántica ha hecho posible el descubrimiento y desarrollo de muchas tecnologías, como por ejemplo los transistores que se usan más que nada en la computación. Igualmente la mecánica cuántica daba cuenta de las propiedades de la estructura atómica y de muchos otros problemas para los cuales la mecánica clásica da predicciones totalmente incorrectas. La descripción que hace la mecánica cuántica de las partículas abandona por el completo la noción de trayectoria, ya que debido al principio de incertidumbre no puede existir un estado cuántico convencional donde posición y el momento tengan valores perfectamente definidos. En su lugar, el objeto fundamental en la descripción cuántica de las partículas no son estados definidos por posición y momentum, es decir punto de un espacio de fases, sino distribuciones sobre un espacio fásico. Estas distribuciones pueden ser dotadas de estructura de espacio de Hilbert.
La mecánica cuántica tal como fue originalmente formulada no incorporaba la teoría de la relatividad en su formalismo, que inicialmente solo podía ser tenida en cuenta mediante teoría de perturbaciones.[7] La parte de la mecánica cuántica que sí incorpora elementos relativistas de manera formal y con diversos problemas, es la mecánica cuántica relativista o ya, de forma más exacta y potente, la teoría cuántica de campos (que incluye a su vez a la electrodinámica cuántica, cromodinámica cuántica y teoría electrodébil dentro del modelo estándar)[8] y más generalmente, la teoría cuántica de campos en espacio-tiempo curvo. La única interacción que no se ha podido cuantificar ha sido la interacción gravitatoria.
La mecánica cuántica es la base de los estudios del átomo, los núcleos y las partículas elementales (siendo ya necesario el tratamiento relativista), pero también en teoría de la información, criptografía y química.
Movimientos de traslación[editar]
Para un cuerpo clásico (y, por tanto, moviéndose en un espacio euclídeo), una traslación es la operación que modifica las posiciones de todos los cuerpos según la fórmula:
donde es un vector constante. Dicha operación puede ser generalizada a otras coordenadas, por ejemplo la coordenada temporal. Obviamente una traslación matemática es una isometría del espacio euclídeo.
En cinemática clásica se utiliza un sistema de coordenadas para describir las trayectorias de traslación, denominado sistema de referencia. El estudio de la cinemática usualmente empieza con la consideración de casos particulares de movimientos de traslación con características particulares. Usualmente se empieza el estudio cinemático considerando el movimiento de un móvil puntual o cuerpo sólido cuya estructura y propiedades internas pueden ignorarse para explicar su movimiento global. Entre los movimientos típicos que puede ejecutar un móvil puntual son particularmente interesantes los siguientes:
Movimientos rectilíneos[editar]
Un movimiento es rectilíneo cuando describe una trayectoria recta. La trayectoria rectilínea se define cuando el componente de aceleración normal es igual a cero. Usualmente se estudian tres casos particulares de movimiento rectilíneo:
- El movimiento rectilíneo uniforme. El móvil recorre la trayectoria a velocidad constante, es decir, con una aceleración nula. Esto implica que la velocidad media entre dos instantes cualesquiera siempre tendrá el mismo valor. Además la velocidad instantánea y media de este movimiento coincidirán. Dinámicamente, el móvil presenta cantidad de movimiento y energía cinética constantes, y de acuerdo a la primera Ley de Newton, la fuerza resultante es de cero.
- El Movimiento rectilíneo uniformemente acelerado es aquel en el que un móvil se desplaza sobre una recta con aceleración constante y colineal con la velocidad. Esto implica que en cualquier intervalo de tiempo, la aceleración del cuerpo tendrá siempre el mismo valor, y que el valor neto de la aceleración resultante corresponde a la aceleración tangencial, mientras que el valor de la aceleración normal es de cero. Por ejemplo la caída libre de un cuerpo, con aceleración de la gravedad constante.

- El movimiento armónico simple es un caso particular de sistema rectilíneo conservativo periódico de vaivén, en el que un cuerpo oscila de un lado al otro de su posición de equilibrio, en una dirección determinada, y en intervalos iguales de tiempo. El móvil se desplaza oscilando alrededor de la posición de equilibrio cuando se separa de ella y regresa al origen. La velocidad y la aceleración varían de manera periódica. El modelo matemático es:
donde:
- es la frecuencia angular del movimiento.
- es la amplitud del movimiento.
- es la fase inicial.
Movimientos curvilíneos[editar]
Un movimiento es curvilíneo cuando describe una trayectoria curva. Se genera una traslación curvilínea cuando existe una componente de aceleración normal a la trayectoria. Cuando un cuerpo realiza un movimiento circular uniforme, la dirección del vector velocidad va cambiando a cada instante. Esta variación la experimenta el vector lineal, debido a una fuerza llamada centrípeta, dirigida hacia el centro de la circunferencia que da origen a la aceleración centrípeta
Cuando una partícula se mueve en una trayectoria curvilínea, aunque se mueva con rapidez constante (por ejemplo el MCU), su velocidad cambia de dirección, ya que esta es un vector tangente a la trayectoria, y en las curvas dicha tangente no es constante.
La aceleración centrípeta, a diferencia de la aceleración centrífuga, está provocada por una fuerza real requerida para que cualquier observador inercial pudiera dar cuenta de como se curva la trayectoria de una partícula que no realiza un movimiento rectilíneo.
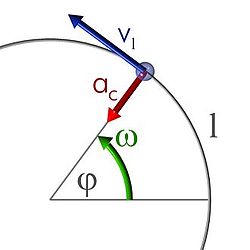
- Movimiento circular. El movimiento circular es el que se basa en un eje de giro y radio constante: la trayectoria será una circunferencia. Si, además, la velocidad de giro es constante, se produce el movimiento circular uniforme, que es un caso particular de movimiento circular, con radio fijo y velocidad angular referente. En este caso la velocidad vectorial no es constante, aunque sí puede ser constante la celeridad (o módulo de la velocidad). La aceleración centrípeta constantemente cambia la dirección de la velocidad tangencial y siempre se mantiene perpendicular a ella.
- Movimiento pendular. El movimiento pendular es una forma de desplazamiento que presentan algunos sistemas físicos como aplicación práctica de movimiento cuasi-armónico. Existen diversas variantes de movimiento pendular: péndulo simple, péndulo de torsión y péndulo físico.
Los tres primeros son de interés tanto en mecánica clásica, como en mecánica relativista y mecánica cuántica. Mientras que el movimiento parabólico y el movimiento pendular son de interés casi exclusivamente en la mecánica clásica. El movimiento armónico simple también es interesante en mecánica cuántica para aproximar ciertas propiedades de los sólidos a nivel atómico.
- Movimiento elíptico. Un movimiento elíptico es un caso de movimiento acotado en el que una partícula describe una trayectoria elíptica. Existen diversos sistemas físicos donde sucede esto, entre ellos el movimiento planetario en un potencial gravitatorio newtoniano.
- Movimientos espirales. Aquellos en donde se combinan un movimiento circular y una velocidad normal o aceleración adicional a la centrípeta. El ejemplo clásico es el movimiento espiral uniforme, en el que las trayectoria corresponde a una espiral de Arquímedes en la cual el móvil puntual se mueve a velocidad constante sobre una recta que gira sobre un punto de origen fijo a velocidad angular constante.

- Movimiento helicoidal es aquel que presenta una trayectoria cuyas tangentes forman un ángulo constante (α), siguiendo una dirección fija en el espacio.
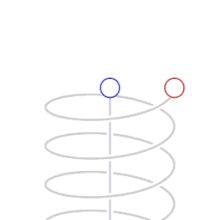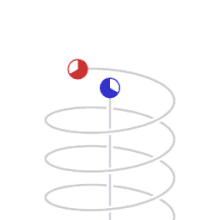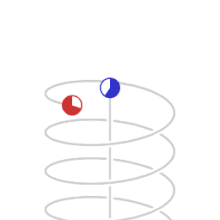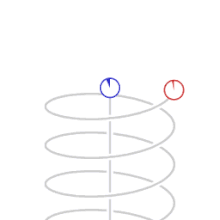
- Movimientos trocoides. Aquellos que describen una trayectoria curva del plano, determinada por un punto fijo de una circunferencia llamada generatriz, la misma que rueda, tangencialmente, sin resbalar sobre una recta nombrada directriz. Se da el nombre de cicloide a la curva descrita por un punto de la circunferencia, cuando esta rueda recorre sin resbalar una recta:

Una curva braquistócrona o curva del descenso más rápido, es la curva entre dos puntos que es recorrida en menor tiempo, por un cuerpo que comienza en el punto inicial con velocidad cero, y que debe desplazarse a lo largo de la curva hasta llegar al segundo punto, bajo acción de una fuerza de gravedad constante y suponiendo que no existe fricción.[9]

Una hipotrocoide, en geometría, es la curva plana que describe un punto vinculado a una circunferencia generatriz que rueda dentro de una circunferencia directriz, tangencialmente, sin deslizamiento.

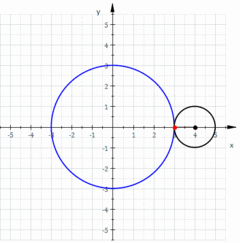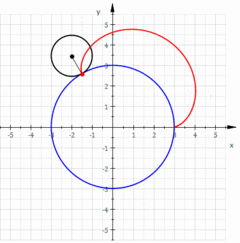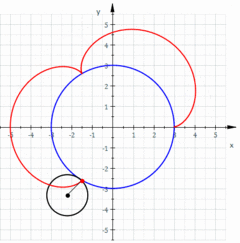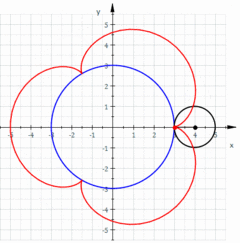
La epicicloide es la curva generada por la trayectoria de un punto perteneciente a una circunferencia (generatriz) que rueda, sin deslizamiento, por el exterior de otra circunferencia (directriz). Es un tipo de ruleta cicloidal.
- Movimiento parabólico. Se denomina movimiento parabólico al realizado por un objeto cuya trayectoria describe una parábola. Se genera cuando un móvil con velocidad de magnitud y dirección constante presenta una aceleración normal neta y la aceleración tangencial es cero. En mecánica clásica se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme. También es posible demostrar que puede ser analizado como la composición de dos movimientos rectilíneos, un movimiento rectilíneo uniforme horizontal y movimiento rectilíneo uniformemente acelerado vertical.
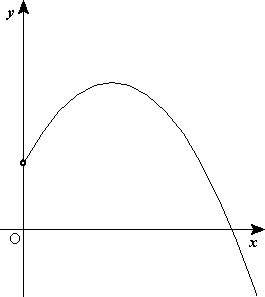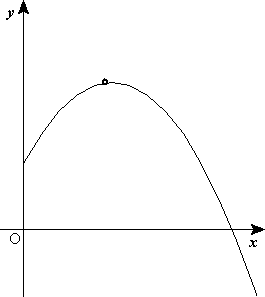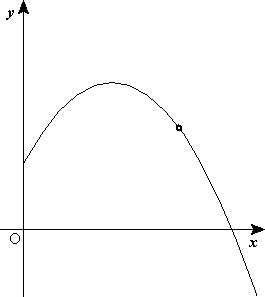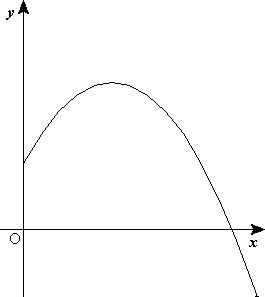
- Movimiento hiperbólico. Movimiento en el que el móvil sigue una trayectoria en forma de hipérbola. En mecánica celeste, un móvil con velocidad superior a la necesaria para escapar de la atracción gravitatoria de un cuerpo central describe una trayectoria hiperbólica.
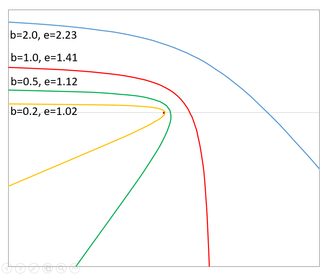
En términos más técnicos, esto puede expresarse por la condición de que la excentricidad orbital sea mayor que uno. En una trayectoria hiperbólica, la anomalía verdadera está vinculada a la distancia entre los cuerpos en órbita () por la ecuación orbital:

- Movimiento de persecución es aquel que describe un objeto (situado en P) que es arrastrado por otro (situado en A), que se mantiene a distancia constante d y que se desplaza en línea recta. Su trayectoria es una tractriz.[10]
- Movimiento ondulatorio o sinusoidal simple, se denomina al movimiento que puede ser analizado como la composición de dos movimientos rectilíneos, un movimiento rectilíneo uniforme horizontal y movimiento rectilíneo armónico simple vertical. Este movimiento se da sobre un medio continuo en el que una perturbación se propaga desde una partícula a las partículas vecinas sino que exista un flujo neto de masa, aun cuando sí haya transporte de energía en el medio. Se corresponde con la trayectoria ideal de un cuerpo que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme.

Movimientos rotatorios[editar]

Las rotaciones tridimensionales revisten especial interés práctico por corresponderse con la geometría del espacio físico en que vivimos (naturalmente siempre que se consideren regiones de escala mediana, ya que para distancias grandes la geometría no es estrictamente euclídea). En tres dimensiones conviene distinguir entre las rotaciones planas o rectangulares, que son aquellas en las que el vector rotado y el que determina el eje de giro forman un ángulo recto, y las cónicas, en las que el ángulo entre estos vectores no es recto. Las rotaciones planas son de tratamiento matemático más simple, pues se pueden reducir al caso bidimensional descrito más arriba, mientras que las cónicas son mucho más complejas y por lo general se tratan como una combinación de rotaciones planas (especialmente los ángulos de Euler y los parámetros de Euler-Rodrigues).
Cuando se estudia el movimiento de un sólido rígido resulta conveniente descomponerlo en un movimiento de traslación más un movimiento de rotación:
- Para describir la traslación solo necesitamos calcular las fuerzas resultantes y aplicar las leyes de Newton como si se tratara de puntos materiales.
- En cambio la descripción de la rotación es más compleja, ya que necesitamos alguna magnitud que de cuenta de como está distribuida la masa alrededor de cierto punto o eje de rotación (por ejemplo un eje que pase por el centro de masa). Esa magnitud es el tensor de inercia que caracteriza la inercia rotacional del sólido.
Ese tensor de inercia sólido rígido se define como un tensor simétrico de segundo orden tal que la forma cuadrática construida a partir del tensor y la velocidad angular ω da la energía cinética de rotación, es decir:
(4)
No solo la energía cinética se puede expresar sencillamente en términos del tensor de inercia, si reescribimos la expresión (3) para el momento angular introduciendo en ella la definición del tensor de inercia, tenemos que este tensor es la aplicación lineal que relaciona la velocidad angular y el momento angular:
(5)
De acuerdo con la mecánica del sólido rígido, además de la rotación alrededor de su eje de simetría, un giróscopo presenta en general dos movimientos principales: la precesión y la nutación.

En un giroscopio debemos tener en cuenta que el cambio en el momento angular de la rueda debe darse en dirección del momento de la fuerza que actúa sobre la rueda.
Movimiento ondulatorio y vibracional[editar]
Se denomina movimiento ondulatorio al realizado por un objeto cuya trayectoria describe una ondulación. Un tipo de movimiento ondulatorio frecuente, el sonido que involucra la propagación en forma de ondas elásticas longitudinales (sean audibles o no), generalmente a través de un fluido (u otro medio elástico) que esté generando el movimiento vibratorio de un cuerpo.
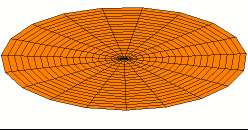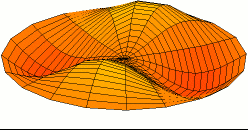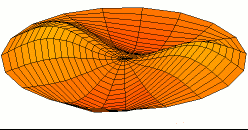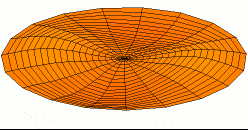
Un movimiento armónico complejo es un movimiento superposición lineal de movimientos armónicos simples. Aunque un movimiento armónico simple es siempre periódico, un movimiento armónico complejo no necesariamente es periódico, aunque sí puede ser analizado mediante análisis armónico de Fourier. Un movimiento armónico complejo es periódico solo si es la combinación de movimientos armónicos simples cuyas frecuencias son todas múltiplos racionales de una frecuencia base. En mecánica clásica, la trayectoria de un movimiento armónico complejo bidimensional es una curva de Lissajous.
Registro del movimiento[editar]
La tecnología hoy en día nos ofrece muchas formas de registrar el movimiento efectuado por un cuerpo. Así, para medir la velocidad se dispone del radar de tráfico cuyo funcionamiento se basa en el efecto Doppler. El taquímetro es un indicador de la velocidad de un vehículo basado en la frecuencia de rotación de las ruedas. Los caminantes disponen de podómetros que detectan las vibraciones características del paso y, suponiendo una distancia media característica para cada paso, permiten calcular la distancia recorrida. El vídeo, unido al análisis informático de las imágenes, permite igualmente determinar la posición y la velocidad de los vehículos.
Movimiento molecular[editar]

La dinámica molecular (DM) es una técnica de simulación en la que se permite que átomos y moléculas interactúen por un período, permitiendo una visualización del movimiento de las partículas. Originalmente fue concebida dentro de la física teórica, aunque hoy en día se utiliza sobre todo en biofísica y ciencia de materiales. Su campo de aplicación va desde superficies catalíticas hasta sistemas biológicos como las proteínas. Si bien los experimentos de cristalografía de rayos X permiten tomar "fotografías estáticas" y la técnica de RMN nos da indicios del movimiento molecular, ningún experimento es capaz de acceder a todas las escalas de tiempo involucradas. Resulta tentador, aunque no es enteramente correcto, describir a la DM como un "microscopio virtual" con alta resolución espacial y temporal.
En general, los sistemas moleculares son complejos y consisten de un gran número de partículas, por lo cual sería imposible encontrar sus propiedades de forma analítica. Para evitar este problema, la DM utiliza métodos numéricos. La DM representa un punto intermedio entre los experimentos y la teoría. Puede ser entendida como un experimento en la computadora.
Sabemos que la materia está constituida de partículas en movimiento e interacción al menos desde la época de Boltzmann en el siglo XIX. Pero muchos aún se imaginan a las moléculas como los modelos estáticos de un museo. Richard Feynman dijo en 1963 que "todo lo que hacen los seres vivos puede ser entendido a través de los saltos y contorsiones de los átomos.
Una de las contribuciones más importantes de la dinámica molecular es crear conciencia de que el DNA y las proteínas son máquinas en movimiento. Se le utiliza para explorar la relación entre estructura, movimiento y función.
La dinámica molecular es un campo multidisciplinario. Sus leyes y teorías provienen de las Matemáticas, Física y Química. Emplea algoritmos de las Ciencias de la Computación y Teoría de la información. Permite entender a los materiales y las moléculas no cómo entidades rígidas, sino como cuerpos animados. También se le ha llamado "estadística mecánica numérica" o "la visión de Laplace de la mecánica Newtoniana", en el sentido de predecir el futuro al animar las fuerzas de la naturaleza.
Para utilizar esta técnica de forma correcta, es importante entender las aproximaciones utilizadas y evitar caer en el error conceptual de que estamos simulando el comportamiento real y exacto de un sistema molecular. La integración de las ecuaciones de movimiento están mal condicionadas, lo cual genera errores numéricos acumulativos, que pueden ser minimizados seleccionando apropiadamente los algoritmos, pero no eliminados del todo. Por otro lado, las interacciones entre las partículas se modelan con un campo de fuerza aproximado, que puede o no ser adecuado dependiendo del problema que queremos resolver. De cualquier forma, la dinámica molecular nos permite explorar su comportamiento representativo en el espacio fásico.
En la DM, hay que balancear el costo computacional y la fiabilidad en los resultados. En la DM clásica se utilizan las Ecuaciones de Newton, cuyo costo computacional es mucho menor que el de las de la mecánica cuántica. Es por ello que muchas propiedades que pueden resultar de interés, como la formación o ruptura de enlace= no puedan ser estudiadas mediante este método ya que no contempla estados excitados o reactividad.
Existen métodos híbridos denominados QM/MM (Quantum Mechanics/Molecular Mechanics) en los que un centro reactivo es tratado de modo cuántico mientras que el ambiente que lo rodea se trata de modo clásico. El desafío en este tipo de métodos resulta en la definición de manera precisa de la interacción entre los dos formas de describir el sistema...
El resultado de una simulación de dinámica molecular son las posiciones y velocidades de cada átomo de la molécula, para cada instante en el tiempo discretizado. A esto se le llama trayectoria.

El movimiento browniano es el movimiento aleatorio que se observa en las partículas que se hallan en un medio fluido (líquido o gas), como resultado de choques contra las moléculas de dicho fluido. Este fenómeno recibe su nombre en honor al escocés Robert Brown, biólogo y botánico. En 1827, mientras miraba a través de un microscopio a las partículas atrapadas en las cavidades dentro de un grano de polen en el agua, señaló que las partículas se movían a través del líquido; pero no fue capaz de determinar los mecanismos que provocaron este movimiento. Los átomos y las moléculas habían sido teorizadas como componentes de la materia, y Albert Einstein publicó un artículo en 1905, donde explicó con todo detalle cómo el movimiento que Brown había observado era el resultado del polen siendo movido por moléculas de agua individuales. La dirección de la fuerza de bombardeo atómico está cambiando constantemente, y en diferentes momentos, la partícula es golpeada más en un lado que en otro, lo que lleva a la naturaleza aleatoria del movimiento.
El movimiento browniano se encuentra entre los procesos estocásticos más simples, y es afín a otros dos procesos estocásticos más simples y complejos: el camino aleatorio y el teorema de Donsker. Esta universalidad está estrechamente relacionada con la universalidad de la distribución normal. En ambos casos, a menudo es la conveniencia matemática, más que exactitud de los modelos, lo que lleva al uso de la distribución normal. Tanto la difusión como la ósmosis se basan en el movimiento browniano.
Véase también[editar]
- Física
- Cantidad de movimiento
- Cinemática del sólido rígido
- Mecánica
- Fuerza de empuje
- Velocidad relativa
- Aceleración centrípeta
Referencias[editar]
- ↑ Robert M. Wald, 1984
- ↑ [1] Definición de la RAE
- ↑ Aristotle's Physics "Física" de Aristóteles traducida al inglés por R. P. Hardie de R. K. Gaye
- ↑ Física - Aristóteles "Física", Bibliotheca Scriptorum Graecorum et Romanorum Mexicana Obras (Aristóteles (Universidad Nacional Autónoma de México))), traducción de Ute Schmidt Osmanczik, UNAM 2001, ISBN 968-36-8136-0, ISBN 978-968-36-8136-2
- ↑ De Broglie (1926): Ondes et mouvements, París, Gauthier-Villars
- ↑ Schrödinger, [Quantisierung als Eigenwertproblem (Erste Mitteilung.)], Ann. Phys., 79, p. 361-376, (1926)1924 & 1926
- ↑ Cohen-Tannoudji, Claude; Bernard Diu, Franck Laloë (1977). Quantum Mechanics. vol.1 (3ª edición). París, Francia: Hermann. pp. 898. ISBN 0-471-16432-1.
- ↑ Halzen, Francis; D.Martin, Alan (1984). Universidad de Wisconsin, ed. Quarks and Lepons: An Introducory Course in Modern Particle Physics. Universidad de Durham (1ª edición). Canadá: Wiley. p. 396. ISBN QC793.5.Q2522H34
|isbn=incorrecto (ayuda). - ↑ Hofmann: Historia de la matemática ISBN 968-18-6286-4
- ↑ I. Bronshtein, K Semendiaev Manual para ingenieros y estudiantes Editorial Mir Moscú (1973)
Bibliografía[editar]
- Una pequeña parte de este artículo corresponde a la información adquirida por el libro enciclopédico Estudios de la naturaleza, Yaditzha Irausquin (2008).
- Physics – Physical Science Study Committee (1966). ISBN 978-0-669-97451-5
- Physics (second edition 1996)






































