Vector
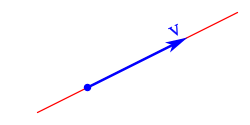
En matemática y física, un vector[a] es cualquier ente matemático que se puede representar mediante un segmento de recta orientado dentro del espacio euclidiano.
Un vector con un origen fijado queda determinado a partir de dos elementos:
- Una semirrecta a partir de dicho origen, es decir, una dirección hacia la que apunta.[b]
- Un número no negativo, llamado módulo del vector y que mide su tamaño.
Alternativamente, se puede fijar un sistema de coordenadas del espacio -dimensional; entonces un vector queda unívocamente determinado mediante números, llamados coordenadas del vector. El ejemplo más sencillo son las coordenadas cartesianas, un sistema de ejes reglados que se suelen tomar perpendiculares entre sí.
Así, fijado un sistema de ejes cartesianos —en otras palabras, un punto origen y una base— un vector tridimensional queda completamente determinado por tres números, llamados coordenadas cartesianas. Más concretamente, dados tres números se puede trazar una flecha o vector siguiendo estos pasos:
- Desplazarse unidades en la dirección del eje .
- Desplazarse unidades en la dirección del eje .
- Desplazarse unidades en la dirección del eje .
- Trazar la flecha desde el punto origen hasta el de llegada.
En matemáticas se define vector como un elemento de un espacio vectorial. Esta noción es más abstracta, ya que para muchos espacios vectoriales no es posible representar sus vectores mediante el módulo y la dirección. En particular los espacios de dimensión infinita sin producto escalar no son representables de ese modo. Los vectores en un espacio euclidiano se pueden representar geométricamente como segmentos de recta , en el plano (bidimensional), o en el espacio (tridimensional).
Por lo tanto, la definición usada en física de vector como un segmento de recta orientado (en el plano o en el espacio) es un caso particular de esta noción. Es posible describir fenómenos físicos mediante magnitudes físicas vectoriales como las siguientes:
- La velocidad de un automóvil. No sería suficiente describirla con tan solo un número, que es lo que marca el velocímetro, sino que se requiere indicar la dirección (hacia donde se dirige).
- La fuerza que actúa sobre un objeto, ya que su efecto depende, además de su magnitud o módulo, de la dirección en la que actúa.
- El desplazamiento de un objeto, pues es necesario definir la distancia que recorre, y la dirección del movimiento, o bien la posición inicial y final del objeto.
Conceptos fundamentales en vectores euclídeos[editar]
Esta sección explica los aspectos básicos, la necesidad de los vectores para representar ciertas magnitudes físicas, los componentes de un vector euclídeo o geométrico, así como la notación de los mismos, etc. En otra sección más adelante se tratan otro tipo de vectores más generales.
Definición[editar]

Un vector es un elemento de un espacio vectorial. En la práctica, cuando se tratan con vectores usualmente se expresan a una base vectorial. Así fijada un espacio vectorial específico y una base dentro del mismo:
Un vector (real) de dimensión viene representado por una tupla de números reales (que se llaman componentes del vector). El conjunto de todos los vectores de dimensión se representa como (formado mediante el producto cartesiano). Así, un vector perteneciente a un espacio se representa como:
, donde
Un vector también se puede ver desde el punto de vista de la geometría como vector geométrico (usando frecuentemente el espacio tridimensional o bidimensional ).
Un vector fijo del plano euclidiano es un segmento orientado, en el que hay que distinguir tres características:[1][2][3]
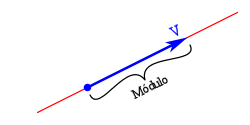
- Módulo: la longitud del segmento expresado en términos de un valor numérico y una unidad.
- Dirección: el ángulo u orientación angular del vector con respecto al eje x. Una dirección puede ser recorrida en dos sentidos opuestos (por ej. puede tener una orientación norte-sur, este-oeste, vertical, horizontal, paralela, etc.).
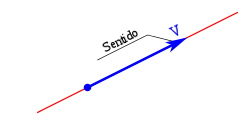
- Sentido: es cada una de las dos orientaciones opuestas de una misma dirección, indicando el origen y extremo (representado en general con la punta de una flecha en un vector) de ésta. Puede ser positivo o negativo.
En inglés, la palabra direction indica tanto la dirección como el sentido del vector, con lo que se define el vector con solo dos características: módulo y dirección.[4]
Los vectores fijos del plano se denotan con dos letras mayúsculas (y una flecha hacia la derecha encima), por ejemplo , que indican su origen y extremo respectivamente. Es decir, el punto A es el origen o punto de aplicación y el punto B es el extremo del vector , cuyas coordenadas son:
Características de un vector[editar]

Un vector se puede definir por sus coordenadas, si el vector está en el plano xy, se representa:
siendo sus coordenadas:
Si consideramos el triángulo formado por los componentes (como catetos) y (como hipotenusa): se puede calcular multiplicando por el (siendo el ángulo formado por y ) o multiplicando por el (siendo el ángulo formado por y ). De igual forma se puede calcular multiplicando por el o multiplicando por el (considerando las posiciones de y mencionadas anteriormente).
Siendo el vector la suma vectorial de sus coordenadas:

Si un vector es de tres dimensiones reales, representado sobre los ejes x, y, z, se puede representar:
siendo sus coordenadas:
Si representamos el vector gráficamente podemos diferenciar los siguientes elementos:
La recta soporte o dirección, sobre la que se traza el vector.

El módulo o amplitud con una longitud proporcional al valor del vector.
El sentido, indicado por la punta de flecha, siendo uno de los dos posibles sobre la recta soporte.
El punto de aplicación que corresponde al lugar geométrico al cual corresponde la característica vectorial representado por el vector.

El nombre o denominación es la letra, secuencia o signo de signos que define al vector.
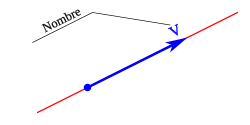
Por lo tanto en un vector podemos diferenciar:

- Nombre
- Dirección
- Sentido
- Módulo
- Punto de aplicación
Magnitudes vectoriales[editar]


Frente a aquellas magnitudes físicas, tales como la masa, la presión, el volumen, la energía, la temperatura, etc; que quedan completamente definidas por un número y las unidades utilizadas en su medida, aparecen otras, tales como el desplazamiento, la velocidad, la aceleración, la fuerza, el campo eléctrico, etc., que no quedan completamente definidas dando un dato numérico, sino que llevan asociadas una dirección. Estas últimas magnitudes son llamadas vectoriales en contraposición a las primeras llamadas escalares.
Las magnitudes vectoriales quedan representadas por un ente matemático que recibe el nombre de vector. En un espacio euclidiano, de no más de tres dimensiones, un vector se representa por un segmento orientado. Así, un vector queda caracterizado por los siguientes elementos: su longitud o módulo, siempre positivo por definición, y su dirección, la cual puede ser representada mediante la suma de sus componentes vectoriales ortogonales, paralelas a los ejes de coordenadas; o mediante coordenadas polares, que determinan el ángulo que forma el vector con los ejes positivos de coordenadas.[5] [6]
Se representa como un segmento orientado, con una dirección, dibujado de forma similar a una "flecha". Su longitud representa el módulo del vector, la recta indica la dirección, y la "punta de flecha" indica su sentido.[1][2][3]
Notación[editar]
Las magnitudes vectoriales se representan en los textos impresos por letras en negrita, para diferenciarlas de las magnitudes escalares que se representan en cursiva. En los textos manuscritos, las magnitudes vectoriales se representan colocando una flecha sobre la letra que designa su módulo (el cual es un escalar).
- Ejemplos
- … representan, respectivamente, las magnitudes vectoriales de módulos A, a, ω, … El módulo de una magnitud vectorial también se representa encerrando entre barras la notación correspondiente al vector: …
- En los textos manuscritos se escribe: … para los vectores y … o … para los módulos.
Cuando convenga, se representan la magnitud vectorial haciendo referencia al origen y al extremo del segmento orientado que la representa geométricamente; así, se designan los vectores representados en la Figura 2 en la forma , … resultando muy útil esta notación para los vectores que representan el desplazamiento.
Además de estas convenciones los vectores unitarios o versores, cuyo módulo es la unidad, se representan frecuentemente con un circunflejo encima, por ejemplo .
Clasificación de vectores[editar]
Según los criterios que se utilicen para determinar la igualdad o equipolencia de dos vectores, pueden distinguirse:
- Vectores libres: no están aplicados en determinado punto.
- Vectores deslizantes: su punto de aplicación puede deslizar a lo largo de su recta de acción.
- Vectores fijos o ligados: están aplicados en un determinado punto.
Podemos referirnos también a:
- Vectores unitarios: vectores de módulo uno.
- Vectores concurrentes o angulares: vectores cuyas direcciones o líneas de acción pasan por un mismo punto. También se les suele llamar angulares porque forman un ángulo entre ellas.
- Vectores opuestos: vectores de igual magnitud y dirección, pero sentidos contrarios.[1] En inglés se dice que son de igual magnitud pero direcciones contrarias, ya que la dirección también indica el sentido.
- Vectores colineales: vectores que comparten una misma recta de acción.
- Vectores paralelos: vectores cuyas líneas de acción son paralelas.
- Vectores coplanarios: vectores cuyas rectas de acción son coplanarias (situadas en un mismo plano).
- Vectores Perpendiculares: son dos vectores que forman un ángulo de 90 grados y su producto escalar es cero.
Componentes de un vector[editar]

Un vector en el espacio euclidiano tridimensional se puede expresar como una combinación lineal de tres vectores unitarios o versores, que son perpendiculares entre sí y constituyen una base vectorial.
En coordenadas cartesianas, los vectores unitarios se representan por , , , ( o u, v, w) paralelos a los ejes , , correspondientes. Los componentes del vector en una base predeterminada pueden escribirse entre paréntesis y separadas con comas:
o expresarse como una combinación de los vectores unitarios definidos en la base vectorial. Así, en un sistema de coordenadas cartesiano, será
Estas representaciones son equivalentes entre sí, y los valores , , , son los componentes de un vector que, salvo que se indique lo contrario, son números reales.
Una representación conveniente de las magnitudes vectoriales es mediante un vector columna o un vector fila, particularmente cuando están implicadas operaciones matrices (tales como el cambio de base), del modo siguiente:
Por ejemplo, los vectores unitarios se expresarían de la siguiente manera:
El lema de Zorn, consecuencia del axioma de elección, permite establecer que todo espacio vectorial admite una base vectorial, por lo que todo vector es representable como el producto de unos componentes respecto a dicha base. Dado un vector, solamente existen un número finito de componentes diferentes de cero.
Representación gráfica de los vectores[editar]
Hay personas que no recomiendan usar gráficos para evitar la confusión de conceptos y la inducción al error, sin investigación que lo corrobore, también es cierto que la memoria se estimula con mejores resultados. Para ello:
- Se llama vector a la representación visual con el símbolo de flecha (un segmento y un triángulo en un extremo).
- La rectitud visual de una flecha o curvatura de la misma, no la hace diferente en símbolo si los dos extremos permanecen en el mismo lugar y orden.
- El que una flecha cierre en sí misma, indica la ausencia de efectos algebraicos.
- Para visualizar la suma de vectores se hará encadenándolos, es decir, uniendo el extremo que tiene un triángulo (final) del primer vector con el extremo que no lo tiene (origen) del segundo vector manteniendo la dirección y distancia, propias al espacio, de sus dos extremos, ya que estas dos cualidades los distingue visualmente de otros vectores.
- Los escalares se representarán con una línea de trazos a modo, exclusivamente, de distinción ya que no siempre pertenecen al espacio de vectores.
Se examinan cada uno de los casos que aparecen en la definición de las operaciones suma de vectores y producto por un escalar:
Suma de vectores[editar]
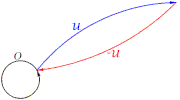
La definición suma de vectores en el orden u+v produce otro vector, es como encadenar, siempre visualmente, un vector u y luego uno v. Diremos que u+v se simplifica como un vector w o que w descompone como suma de vectores u y v.

- 1) Decir que u+v=v+u, es exigir que las dos sumas simplifiquen en el mismo vector, en negro. Véase que en física los vectores en rojo simulan la descomposición de fuerzas ejercidas por el vector negro en su origen, y se representa con un paralelogramo.

- 2) Decir que u+(v+w)=(u+v)+w, es exigir que las simplificaciones de sumas de vectores puedan ser optativas en cualquier cadena de sumas.

- 3) Decir que existe un vector cero (elemento neutro) tal que u+0=u, equivale a exigir que exista un vector incapaz de efectuar, mediante la suma, modificación alguna a todos los vectores.

- 4) Decir que u+(-u)=0, es exigir la existencia de un elemento opuesto, -u, que sumado a u simplifique en un vector cero.
Producto por un escalar[editar]
La definición producto por un escalar produce otro vector; es como modificar el extremo final del vector u, siempre visualmente.
Por un lado, la representación del producto en el caso de que el cuerpo de los escalares sea modifica, visualmente, la longitud de la imagen del vector, quedando ambos siempre superpuestos; por otro lado, las representaciones en el caso de que además de modificar la longitud, también agrega rotaciones, para facilitarlas visualmente considérense centradas en el origen del vector, siendo estas modificaciones un poco más expresivas, visualmente, pero no más fáciles que en el caso real:

- a)Decir que a(bu)=(ab)u, es exigir que los productos encadenados a(b(u)) pueden simplificarse como uno, c=ab, luego (ab)u queda como cu.
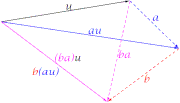
- b) Decir que existe el escalar 1 tal que 1u=u, equivale a decir exista un escalar incapaz de efectuar, mediante producto, modificación alguna a todos los vectores.

- c) Decir que a(u+v)=au+av, es exigir la propiedad distributiva respecto la suma vectorial.

- d) Decir que (a+b)u=au+bu, es exigir la propiedad distributiva respecto la suma escalar.

Para el caso real se han de eliminar las rotaciones de los ejemplos anteriores.
Operaciones con vectores euclídeos[editar]
Suma de vectores[editar]
Para sumar dos vectores libres (vector y vector) se escogen como representantes dos vectores tales que el extremo final de uno coincida con el extremo origen del otro vector.
Suma de vectores sobre un mismo punto[editar]
La suma de vectores está bien definida si ambos vectores pertenecen al mismo espacio vectorial, en física para que dos vectores puedan ser sumados deben estar aplicados en el mismo punto. La composición de fuerzas sobre un sólido rígido cuando los puntos de aplicación no coinciden lleva a la noción de momento de fuerza dados dos fuerzas con puntos de aplicación se definen la fuerza resultante como el par:[cita requerida]
Donde es la suma generalizada a vectores aplicados en diferentes puntos. El punto de aplicación es el punto de intersección de las rectas de acción de las fuerzas. Los componentes del vector de fuerza resultante es de hecho la suma de componentes ordinarias de vectores:
El momento resultante es el momento de fuerza del conjunto de fuerzas respecto al punto calculado para la fuerza resultante.
Método del paralelogramo[editar]

Este método permite solamente sumar vectores de dos en dos. Consiste en disponer gráficamente los dos vectores de manera que los orígenes de ambos coincidan en un punto, trazando rectas paralelas a cada uno de los vectores, en el extremo del otro y de igual longitud, formando así un paralelogramo (ver gráfico). El vector resultado de la suma es la diagonal de dicho paralelogramo que parte del origen común de ambos vectores.
Método del triángulo o método poligonal[editar]

Consiste en disponer gráficamente un vector a continuación de otro, ordenadamente: el origen de cada uno de los vectores coincidirá con el extremo del siguiente. El vector resultante es aquel cuyo origen coincide con el del primer vector y termina en el extremo del último.
Método analítico para la suma y diferencia de vectores[editar]
Dados dos vectores libres,
El resultado de su suma o de su diferencia se expresa en la forma
y ordenando los componentes,
Con la notación matricial sería
Conocidos los módulos de dos vectores dados, y , así como el ángulo que forman entre sí, el módulo de es:
La deducción de esta expresión puede consultarse en deducción del módulo de la suma.
Producto de un vector por un escalar[editar]

El producto de un vector por un escalar es otro vector cuyo módulo es el producto del escalar por el módulo del vector, cuya dirección es igual a la del vector, y cuyo sentido es contrario a este si el escalar es negativo.
Partiendo de la representación gráfica del vector, sobre la misma línea de su dirección tomamos tantas veces el módulo de vector como indica el escalar.
Sean un escalar y un vector, el producto de por se representa y se realiza multiplicando cada una de los componentes del vector por el escalar; esto es,
Con la notación matricial sería
Producto escalar[editar]
Producto vectorial[editar]
Derivada ordinaria de un vector[editar]
Dado un vector que es función de una variable independiente
Calculamos la derivada ordinaria del vector con respecto de la variable t, calculando la derivada de cada una de sus componentes como si de escalares se tratara:
teniendo en cuenta que los vectores unitarios son constantes en módulo y dirección.
Con notación matricial sería

Veamos un ejemplo de derivación de un vector, partiendo de una función vectorial:
Esta función representa una curva helicoidal alrededor del eje z, de radio unidad, como se ilustra en la figura. Podemos imaginar que esta curva es la trayectoria de una partícula y la función representa el vector posición en función del tiempo t. Derivando tendremos:
Realizando la derivada:
La derivada del vector posición respecto al tiempo es la velocidad, así que esta segunda función determina el vector velocidad de la partícula en función del tiempo, podemos escribir:
Este vector velocidad es un vector tangente a la trayectoria en el punto ocupado por la partícula en cada instante. El sentido es hacia los valores crecientes de los valores escalares.[4] Si derivásemos de nuevo obtendríamos el vector aceleración.
Derivada covariante de un vector[editar]
Cuando en lugar de emplear una "base fija" en todo el dominio de un vector se usan "bases móviles" como cuando se emplean coordenadas curvilíneas la variación total de un vector dependiente del tiempo depende no solo de la variación de componentes como en el caso de la derivada ordinaria sino también de la variación de la orientación de la base. La variación total se llama derivada covariante:
Cuando se emplea una base fija (coordenadas cartesianas) la derivada covariante coincide con la derivada ordinaria. Por ejemplo cuando se estudia el movimiento de una partícula desde un sistema de referencia no inercial en rotación, las aceleraciones de Coriolis y centrípeta se deben a los factores que contienen y otros factores menos comunes.
Ángulo entre dos vectores[editar]
El ángulo determinado por las direcciones de dos vectores y viene dado por:
Descomposiciones de un vector[editar]
Dado un vector y una dirección de referencia dada por un vector unitario se puede descomponer el primer vector en un componente paralela y otro componente perpendicular a la dirección de referencia:
En física esta descomposición se usa en diferentes contextos como descomponer la aceleración en un componente paralela a la velocidad y otro componente perpendicular a la misma. También el tensión mecánica en un punto sobre un plano puede descomponerse en un componente normal al plano y otra paralela.
También dado un campo vectorial definido sobre un dominio de Lipschitz, acotado, simplemente conexo y de cuadrado integrable admite la llamada descomposición Helmholtz como suma de un campo conservativo y un campo solenoidal:
Cambio de base vectorial[editar]

En matemáticas las rotaciones son transformaciones lineales que conservan las normas en espacios vectoriales en los que se ha definido una operación de producto interno. La matriz de transformación tiene la propiedad de ser una matriz unitaria, es decir, es ortogonal y su determinante es 1. Sea un vector expresado en un sistema de coordenadas cartesianas (x, y, z) con una base vectorial asociada definida por los versores ; esto es,
Ahora, supongamos que giramos el sistema de ejes coordenados, manteniendo fijo el origen del mismo, de modo que obtengamos un nuevo triedro ortogonal de ejes (x′, y′, z′), con una base vectorial asociada definida por los versores . Los componentes del vector en esta nueva base vectorial serán:
La operación de rotación de la base vectorial siempre puede expresarse como la acción de un operador lineal (representado por una matriz) actuando sobre el vector (multiplicando al vector):
que es la matriz de transformación para el cambio de base vectorial.
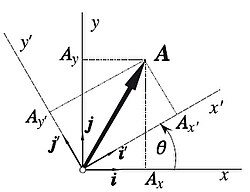
- Ejemplo
En el caso simple en el que el giro tenga magnitud alrededor del eje z, tendremos la transformación:
Al hacer la aplicación del operador, es decir, al multiplicar la matriz por el vector, obtendremos la expresión del vector en la nueva base vectorial:
siendo
los componentes del vector en la nueva base vectorial.
Vectores en el caso general[editar]
En matemáticas, se define la estructura de espacio vectorial y a cada uno de los elementos o puntos de ese espacio se les denomina vector. En muchos casos los vectores no pueden ser representados por módulo dirección y sentido. Por ejemplo, en un espacio vectorial complejo sobre los números complejos la noción de módulo no está automáticamente defindida. Igualmente en un espacio vectorial de dimensión infinita, como es el caso de espacios de Hilbert no existe una representación gráfica de los vectores como segmentos orientados.
Requerimientos físicos de las magnitudes vectoriales[editar]
No cualquier n-tupla de funciones o números reales constituye un vector físico. Para que una n-tupla represente un vector físico, los valores numéricos de los componentes del mismo medidos por diferentes observadores deben transformarse de acuerdo con ciertas relaciones fijas.
En mecánica newtoniana generalmente se utilizan vectores genuinos, llamados a veces vectores polares, junto con pseudovectores, llamados vectores axiales que realmente representan el dual de Hodge de magnitudes tensoriales antisimétricas. El momento angular, el campo magnético y todas las magnitudes en cuya definición interviene el producto vectorial son en realidad pseudovectores o vectores axiales.
En teoría de la relatividad especial, solamente los vectores tetradimensionales cuyas medidas tomadas por diferentes observadores pueden ser relacionadas mediante alguna transformación de Lorentz constituyen magnitudes vectoriales. Así los componentes de dos magnitudes vectoriales medidas por dos observadores y deben relacionarse de acuerdo con la siguiente relación:
Donde son los componentes de la matriz que da la transformación de Lorentz. Magnitudes como el momento angular, el campo eléctrico o el campo magnético de hecho en teoría de la relatividad no son magnitudes vectoriales sino tensoriales.
Véase también[editar]
Notas[editar]
- ↑ También llamado vector euclidiano o vector geométrico para distinguirlo del concepto más genérico de espacio vectorial o de otras acepciones.[cita requerida]
- ↑ En los textos en castellano, es habitual con dirección referirse a una recta (o una familia de rectas paralelas), y con sentido a una de las dos semirrectas (o familias de semirrectas paralelas). «2». Compendio de Física. Editorial San Marcos. 2018. ISBN 978-612-315-362-5.
Referencias[editar]
- ↑ a b c Enrico Bompiani, Universidad Nacional del Litoral, ed., Geometría Analítica, pp. 14-15, ISBN 9789875084339.
- ↑ a b Llopis, GÁlvez, Rubio, López (1998), Editorial Tebar, ed., Física: curso teórico-práctico de fundamentos físicos de la ingeniería, p. 26-27,36,70,71,82, ISBN 9788473601870, «(cito algunos ejemplos) [de página 26] [Otras magnitudes] llamadas vectoriales, donde no basta conocer su valor numerico, sino que además es necesario dar también su dirección y sentido. [página 70] […] el cual es un vector que en general tendrá distinta dirección y sentido que r(t). [página 71] […] Consecuencia de la definición es que la dirección de este vector derivada, dr/dt, es tangente a la curva indicatriz, su sentido es el de los valors crecientes del parámetro escalar t, y que su módulo es: […]».
- ↑ a b Manuela Blanco Sánchez, Marcial Carreto Sánchez, José Ma González Clouté (1997), Ediciones de la Torre, ed., Programa de diversificación curricular: ámbito científico-tecnológico: 2o. ciclo de ESO, Proyecto Didáctico Quirón. Ciencias y tecnología 102 (ilustrada edición), pp. 200,202,216, ISBN 9788479601867.
- ↑ a b Mitiguy, Paul, Chapter 2: Vectors and dyadics (en inglés), p. nota 1 en página 2, archivado desde el original el 20 de noviembre de 2012, consultado el 12 de febrero de 2012.
- ↑ «Euclidean vector» (en inglés). PlanetMath.org. Archivado desde el original el 6 de marzo de 2016. Consultado el 3 de junio de 2010.
- ↑ «Vector» (en inglés). Math Academy Online. Archivado desde el original el 28 de octubre de 2012. Consultado el 3 de junio de 2010.
Bibliografía[editar]
- Ortega, Manuel R. (1989-2006). Lecciones de Física (4 volúmenes). Monytex. ISBN ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7
|isbn=incorrecto (ayuda). - Resnick, Robert & Krane, Kenneth S. (2001). Physics (en inglés). New York: John Wiley & Sons. ISBN 0-471-32057-9.
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (en inglés) (6.ª edición). Brooks/Cole. ISBN 0-534-40842-7.
- Tipler, Paul A. (2000). Física para la ciencia y la tecnología (2 volúmenes). Barcelona: Ed. Reverté. ISBN 84-291-4382-3.
Enlaces externos[editar]
 Wikcionario tiene definiciones y otra información sobre vector.
Wikcionario tiene definiciones y otra información sobre vector.- Weisstein, Eric W. «Vector». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.

















































![{\displaystyle \mathbf {a} ={\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\\\end{bmatrix}}\qquad \mathbf {a} =[a_{x}\ a_{y}\ a_{z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74dd5bf24782a78879c23ed46b4f08fdc7e16421)
![{\displaystyle {\mathbf {i} }=[1\ 0\ 0],\ {\mathbf {j} }=[0\ 1\ 0],\ {\mathbf {k} }=[0\ 0\ 1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07c3a1a35a66b5e4b06fe445b3fba02953572873)

























































