Combinación lineal
En matemáticas, particularmente en álgebra lineal, una combinación lineal es una expresión matemática que consiste en la suma entre pares de elementos, de determinados conjuntos, multiplicados entre sí.
En particular, la combinación lineal de un sistema de vectores se trata de un vector de la forma
con los elementos de un cuerpo. La definición, provista de esta manera, da lugar a otras definiciones y herramientas importantes, como son los conceptos de independencia lineal y base de un espacio vectorial.
Definición[editar]
Dados dos conjuntos cualesquiera A y B.
|
Resulta de especial interés la definición de combinación lineal de vectores con respecto a un conjunto de escalares.
Espacios vectoriales[editar]
Dado un espacio vectorial V sobre un cuerpo y un conjunto de vectores en V, es decir, .
|
En términos no tan formales, diremos que es combinación lineal de vectores de si podemos expresarlo como una suma de productos por escalar de una cantidad finita de elementos de . En este caso, también se dice que depende linealmente de los vectores de .[1]
Ejemplos[editar]
-
La terna ordenada (20, 12, 37) es una combinación lineal de (1, 3, 5) y (6, 2, 9):
-
En general, dado un vector v en un espacio vectorial, todo múltiplo suyo es combinación lineal. Para el caso particular , sus múltiplos son vectores en el plano con la misma dirección, es decir, paralelos.
-
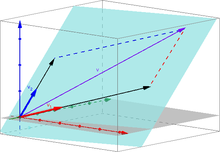
Dado , decir que v es combinación lineal de otros dos vectores no paralelos equivale a afirmar que los tres vectores son coplanarios, es decir, que se encuentran en un mismo plano.
- En la ecuación se dice que es combinación lineal de y de , porque podemos escribir sin más que despejar la . De la misma manera, despejando oportunamente, cada una de estas variables se podría expresar como combinación lineal de las otras dos.
Espacio generado[editar]
Dado un conjunto de vectores A del espacio vectorial V, finito o infinito, se llama espacio generado, denotado como , al conjunto:[2]
donde es el cuerpo sobre el cual está definido V. En términos menos formales, el espacio generado a partir de A es el conjunto de todas las combinaciones lineales que pueden formarse con los vectores de A. Dicho conjunto es el mínimo subespacio vectorial de V que contiene al conjunto A.[cita requerida]
Véase también[editar]
- Sistema generador
- Independencia lineal
- Base (álgebra)
- Base Ortogonal
- Base Ortonormal
- Coordenadas cartesianas
- Producto escalar
- Producto vectorial
- Producto mixto
- Producto tensorial
Referencias[editar]
- ↑ De Burgos, Juan (2006). Álgebra lineal y geometría cartesiana (3ª edición). McGraw-Hill. p. 26. ISBN 9788448149000. Consultado el 27 de enero de 2015.
- ↑ Poole, David (2011). Álgebra lineal (3.ª edición). Cengage Learning. p. 96. ISBN 9786074816082.






















