Coordenadas polares

Las coordenadas polares o sistema de coordenadas polares son un sistema de coordenadas bidimensional en el que cada punto del plano se determina por una distancia y un ángulo. Este sistema es ampliamente utilizado en física y trigonometría.
De manera más precisa, como sistema de referencia se toma: (a) un punto O del plano, al que se llama origen o polo; y (b) una recta dirigida (o rayo, o segmento OL) que pasa por O, llamada eje polar (equivalente al eje x del sistema cartesiano). Con este sistema de referencia y una unidad de medida métrica (para poder asignar distancias entre cada par de puntos del plano), todo punto P del plano corresponde a un par ordenado (r, θ) donde r es la distancia de P al origen y θ es el ángulo formado entre el eje polar y la recta dirigida OP que va de O a P. El valor θ crece en sentido antihorario y decrece en sentido horario. La distancia r (r ≥ 0) se conoce como la «coordenada radial» o «radio vector», mientras que el ángulo es la «coordenada angular» o «ángulo polar».
En el caso del origen, O, el valor de r es cero, pero el valor de θ es indefinido. En ocasiones se adopta la convención de representar el origen por (0,0°).
Historia[editar]

Si bien existen testimonios de que los conceptos de ángulo y radio se conocen y manejan desde la antigüedad, no es sino hasta el siglo XVII, posterior a la invención de la geometría analítica, cuando se puede hablar del concepto formal de sistema coordenadas polares.
Los primeros usos empíricos de relaciones entre ángulos y distancias se relacionan con aplicaciones a la navegación y el estudio de la bóveda celeste. El astrónomo Hiparco (190 a. C.-120 a. C.) creó una tabla trigonométrica que daba la longitud de una cuerda en función del ángulo. También existen referencias del uso de coordenadas polares para establecer la posición de las estrellas.[1] En el tratado Sobre las espirales, Arquímedes describe la llamada espiral de Arquímedes, una función cuyo radio depende del ángulo. Sin embargo, estas aplicaciones no hacían uso de un sistema de coordenadas como medio de localizar puntos en el plano, situación análoga al estado de la geometría antes de la invención de la geometría analítica.
En tiempos modernos, Grégoire de Saint-Vincent y Bonaventura Cavalieri introdujeron de forma independiente el concepto de coordenada polar a mediados del siglo XVII en la solución de problemas geométricos. Saint-Vincent escribió sobre este tema en 1625 y publicó sus trabajos en 1647, mientras que Cavalieri publicó sus escritos en 1635 y una versión corregida en 1653. Cavalieri utilizó en primer lugar las coordenadas polares para resolver un problema relacionado con el área dentro de una espiral de Arquímedes. Blaise Pascal utilizó posteriormente las coordenadas polares para calcular la longitud de arcos parabólicos.
Sin embargo, el concepto abstracto de sistema de coordenada polar se debe a sir Isaac Newton, quien en su Método de las fluxiones escrito en 1671 y publicado en 1736, introduce ocho nuevos sistemas de coordenadas (además de las cartesianas) para resolver problemas relativos a tangentes y curvas, uno de los cuales, el séptimo, es el de coordenadas polares.[2] En el periódico Acta Eruditorum Jacob Bernoulli utilizó en 1691 un sistema con un punto en una línea, llamándolos polo y eje polar respectivamente. Las coordenadas se determinaban mediante la distancia al polo y el ángulo respecto al eje polar. El trabajo de Bernoulli sirvió de base para encontrar el radio de curvatura de ciertas curvas expresadas en este sistema de coordenadas.
El término actual de coordenadas polares se atribuye a Gregorio Fontana, y fue utilizado por los escritores italianos del siglo XVIII. El término aparece por primera vez en inglés en la traducción de 1816 efectuada por George Peacock del Tratado del cálculo diferencial y del cálculo integral de Sylvestre François Lacroix,[3] mientras que Alexis Clairaut fue el primero que pensó en ampliar las coordenadas polares a tres dimensiones.
Representación de puntos con coordenadas polares[editar]

- El punto (3, 60°) indica que está a una distancia de 3 unidades desde O, medidas con un ángulo de 60° sobre OL.
- El punto (4, 210°) indica que está a una distancia de 4 unidades desde O y un ángulo de 210° sobre OL.
Un aspecto a considerar en los sistemas de coordenadas polares es que un único punto del plano puede representarse con un número infinito de coordenadas diferentes, lo cual no sucede en el sistema de coordenadas cartesianas. O sea que en el sistema de coordenadas polares no hay una correspondencia biunívoca entre los puntos del plano y el conjunto de las coordenadas polares. Esto ocurre por dos motivos:
- Un punto, definido por un ángulo y una distancia, es el mismo punto que el indicado por ese mismo ángulo más un número de revoluciones completas y la misma distancia. En general, el punto (, θ) se puede representar como (, θ ± ×360°) o (−, θ ± (2 + 1)180°), donde es un número entero cualquiera.[4]
- El centro de coordenadas está definido por una distancia nula, independientemente de los ángulos que se especifiquen. Normalmente se utilizan las coordenadas arbitrarias (0, θ) para representar el polo, ya que independientemente del valor que tome el ángulo θ, un punto con radio 0 se encuentra siempre en el polo.[5] Estas circunstancias deben tenerse en cuenta para evitar confusiones en este sistema de coordenadas. Para obtener una única representación de un punto, se suele limitar a números no negativos ≥ 0 y θ al intervalo [0, 360°] o [−180°, 180°] (en radianes, [0, 2π] o [−π, π]).[6]
Los ángulos en notación polar se expresan normalmente en grados o en radianes, dependiendo del contexto. Por ejemplo, las aplicaciones de navegación marítima utilizan las medidas en grados, mientras que algunas aplicaciones físicas (especialmente la mecánica rotacional) y la mayor parte del cálculo matemático expresan las medidas en radianes.[7]
Conversión de coordenadas[editar]
Paso de coordenadas polares a rectangulares y viceversa[editar]
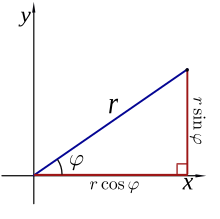
En el plano de ejes xy con centro de coordenadas en el punto O se puede definir un sistema de coordenadas polares de un punto M del plano, definidas por la distancia r al centro de coordenadas, y el ángulo del vector de posición sobre el eje x.
Conversión de coordenadas polares a rectangulares[editar]
Definido un punto en coordenadas polares por su ángulo sobre el eje x, y su distancia r al centro de coordenadas, se tiene:
Conversión de coordenadas rectangulares a polares[editar]
Definido un punto del plano por sus coordenadas rectangulares (x,y), se tiene que la coordenada polar r es:
- (aplicando el Teorema de Pitágoras)
Para determinar la coordenada angular θ, se deben distinguir dos casos:
- Para = 0, el ángulo θ puede tomar cualquier valor real.
- Para ≠ 0, para obtener un único valor de θ, debe limitarse a un intervalo de tamaño 2π. Por convención, los intervalos utilizados son [0, 2π) y (−π, π].
Para obtener θ en el intervalo [0, 2π), se deben usar las siguientes fórmulas ( denota la inversa de la función tangente):
Para obtener en el intervalo , se considera que es una función creciente en su dominio:
Muchos lenguajes de programación modernos evitan tener que almacenar el signo del numerador y del denominador gracias a la implementación de la función atan2, que tiene argumentos separados para el numerador y el denominador. En los lenguajes que permiten argumentos opcionales, la función atan puede recibir como parámetro la coordenada x (como ocurre en Lisp).
Ecuaciones polares[editar]
Se le llama ecuación polar a la ecuación que define una curva expresada en coordenadas polares. En muchos casos se puede especificar tal ecuación definiendo como una función de θ. La curva resultante consiste en una serie de puntos en la forma ((θ), θ) y se puede representar como la gráfica de una función .
Se pueden deducir diferentes formas de simetría de la ecuación de una función polar . Si (−θ) = (θ) la curva será simétrica respecto al eje horizontal (0°/180°), si (180°−θ) = (θ) será simétrica respecto al eje vertical (90°/ 270°), y si (θ−α°) = (θ) será simétrico rotacionalmente α° en sentido horario respecto al polo.
Debido a la naturaleza circular del sistema de coordenadas polar, muchas curvas se pueden describir con una simple ecuación polar, mientras que en su forma cartesiana sería mucho más intrincado. Algunas de las curvas más conocidas son la rosa polar, la espiral de Arquímedes, la lemniscata, el caracol de Pascal y la cardioide.
Para los apartados siguientes se entiende que el círculo, la línea y la rosa polar no tienen restricciones en el dominio y rango de la curva.
Circunferencia[editar]
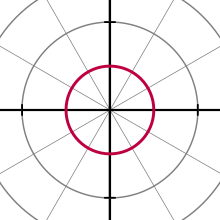
La ecuación general para una circunferencia con centro en (0, φ) y radio es
En ciertos casos específicos, la ecuación anterior se puede simplificar. Por ejemplo, para una circunferencia con centro en el polo y radio a, se obtiene:[8]
Línea[editar]
Las líneas radiales (aquellas que atraviesan el polo) se representan mediante la ecuación
donde φ es el ángulo de elevación de la línea, esto es, φ = arctan donde es la pendiente de la línea en el sistema de coordenadas cartesianas. La línea no radial que cruza la línea radial θ = φ perpendicularmente al punto (0, φ) tiene la ecuación
Rosa polar[editar]

La rosa polar es una famosa curva matemática que parece una flor con pétalos, y puede expresarse como una ecuación polar simple,
para cualquier constante (incluyendo al 0). Si k es un número entero, estas ecuaciones representan una rosa de k pétalos cuando k es impar, o 2k pétalos si k es par. Si k es racional, pero no entero, la gráfica es similar a una rosa, pero con los pétalos solapados. Nótese que estas ecuaciones nunca definen una rosa con 2, 6, 10, 14, etc., pétalos. La variable a representa la longitud de los pétalos de la rosa.
Si tomamos solo valores positivos para r y valores en el intervalo para , la gráfica de la ecuación:
es una rosa de k pétalos, para cualquier número natural . Y si , la gráfica es una circunferencia de radio
Espiral de Arquímedes[editar]

La espiral de Arquímedes es una famosa espiral descubierta por Arquímedes, la cual puede expresarse también como una ecuación polar simple. Se representa con la ecuación
Un cambio en el parámetro a producirá un giro en la espiral, mientras que b controla la distancia entre los brazos, la cual es constante para una espiral dada. La espiral de Arquímedes tiene dos brazos, uno para θ > 0 y otro para θ < 0. Los dos brazos están conectados en el polo. La imagen especular de un brazo sobre el eje vertical produce el otro brazo. Esta curva fue una de las primeras curvas, después de las secciones cónicas, en ser descritas en tratados matemáticos. Además es el principal ejemplo de curva que puede representarse de forma más fácil con una ecuación polar.
Otros ejemplos de espirales son la espiral logarítmica y la espiral de Fermat.
Secciones cónicas[editar]

Una sección cónica con un foco en el polo y el otro en cualquier punto del eje horizontal (de modo que el semieje mayor de la cónica descanse sobre el eje polar) es dada por:
donde e es la excentricidad y es el semilado recto (la distancia perpendicular a un foco desde el eje mayor a la curva). Si e > 1, esta ecuación define una hipérbola; si e = 1, define una parábola; y si e < 1, define una elipse. Para la elipse, el caso especial e = 0 resulta en un círculo de radio .
Números complejos[editar]


Cada número complejo se puede representar como un punto en el plano complejo, y se puede expresar, por tanto, como un punto en coordenadas cartesianas o en coordenadas polares. El número complejo z se puede representar en forma rectangular como
donde i es la unidad imaginaria. De forma alternativa, se puede escribir en forma polar (mediante las fórmulas de conversión dadas arriba) como
por lo que se deduce que
donde e es la constante de Napier.[9] Esta expresión es equivalente a la mostrada en la fórmula de Euler. (Nótese que en esta fórmula, al igual que en todas aquellas en las que intervienen exponenciales de ángulos, se asume que el ángulo θ está expresado en radianes.) Para pasar de la forma polar a la forma rectangular de un número complejo dado se pueden usar las fórmulas de conversión vistas anteriormente.
Para las operaciones de multiplicación, división y exponenciación de números complejos, es normalmente mucho más simple trabajar con números complejos expresados en forma polar que con su equivalente en forma rectangular:
- Multiplicación:
- División:
- Exponenciación (fórmula de De Moivre):
Cálculo infinitesimal[editar]
El cálculo infinitesimal puede ser aplicado a las ecuaciones expresadas en coordenadas polares. A lo largo de esta sección se expresa la coordenada angular θ en radianes, al ser la opción convencional en el análisis matemático.[10][11]
Cálculo diferencial[editar]
Partiendo de las ecuaciones de conversión entre coordenadas rectangulares y polares, y tomando derivadas parciales se obtiene
Para encontrar la pendiente en cartesianas de la recta tangente a una curva polar r(θ) en un punto dado, la curva debe expresarse primero como un sistema de ecuaciones paramétricas
Diferenciando ambas ecuaciones respecto a θ resulta
Dividiendo la segunda ecuación por la primera se obtiene la pendiente cartesiana de la recta tangente a la curva en el punto (r, r(θ)):
Cálculo integral[editar]
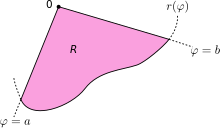
Sea R una región del plano delimitada por la curva continua r(θ) y las semirrectas θ = a y θ = b, donde 0 < b − a < 2π. Entonces, el área de R viene dado por
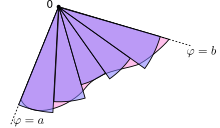
Este resultado puede obtenerse de la siguiente manera. En primer lugar, el intervalo [a, b] se divide en n subintervalos, donde n es un entero positivo cualquiera. Por lo tanto Δθ, la longitud de cada subintervalo, es igual a b − a (la longitud total del intervalo) dividido por n (el número de subintervalos). Para cada subintervalo i = 1, 2, …, n, sea θi su punto medio. Se puede construir un sector circular con centro en el polo, radio r(θi), ángulo central Δθ y longitud de arco . El área de cada sector es entonces igual a
- .
Por lo tanto, el área total de todos los sectores es
Cuanto mayor sea n, mejor es la aproximación al área. En el límite, cuando n → ∞, la suma pasa a ser una suma de Riemann, y por tanto converge en la integral
Generalización[editar]
Usando las coordenadas cartesianas, un elemento de área infinitesimal puede ser calculado como dA = dx dy. El método de integración por sustitución para las integrales múltiples establece que, cuando se utiliza otro sistema de coordenadas, debe tenerse en cuenta la matriz de conversión Jacobiana:
Por lo tanto, un elemento de área en coordenadas polares puede escribirse como:
Una función en coordenadas polares puede ser integrada como sigue:
donde R es la región comprendida por una curva r(θ) y las rectas θ = a y θ = b.
La fórmula para el área de R mencionada arriba se obtiene tomando f como una función constante igual a 1. Una de las aplicaciones de estas fórmulas es el cálculo de la Integral de Gauss :
Cálculo vectorial[editar]
El cálculo vectorial puede aplicarse también a las coordenadas polares. Sea el vector de posición , con r y dependientes del tiempo t.
Sea
un vector unitario en la dirección de y
un vector unitario ortogonal a . Las derivadas primera y segunda del vector de posición son:
Extensión a más de dos dimensiones[editar]
Tres dimensiones[editar]
El sistema de coordenadas polares puede extenderse a tres dimensiones con dos sistemas de coordenadas diferentes: el sistema de coordenadas cilíndricas y el sistema de coordenadas esféricas. El sistema de coordenadas cilíndricas añade una coordenada de distancia, mientras que el sistema de coordenadas esféricas añade una coordenada angular.
Coordenadas cilíndricas[editar]

El sistema de coordenadas cilíndricas es un sistema de coordenadas que extiende al sistema de coordenadas polares añadiendo una tercera coordenada que mide la altura de un punto sobre el plano, de la misma forma que el sistema de coordenadas cartesianas se extiende a tres dimensiones. La tercera coordenada se suele representar por h, haciendo que la notación de dichas coordenadas sea (r, θ, h).
Las coordenadas cilíndricas pueden convertirse en coordenadas cartesianas de la siguiente manera:
Coordenadas esféricas[editar]
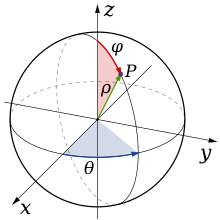
Las coordenadas polares también pueden extenderse a tres dimensiones usando las coordenadas (ρ, φ, θ), donde ρ es la distancia al origen, φ es el ángulo con respecto al eje z (medido de 0° a 180°), y θ es el ángulo con respecto al eje x (igual que en las coordenadas polares, entre 0° y 360°). Este sistema de coordenadas es similar al sistema utilizado para denotar la altitud y la latitud de un punto en la superficie de la Tierra, donde se sitúa el origen en el centro de la Tierra, la latitud δ es el ángulo complementario de φ (es decir, δ = 90° − φ), y la longitud l viene dada por θ − 180°.[12]
Las coordenadas esféricas pueden convertirse en coordenadas cartesianas de la siguiente manera:
Las coordenadas polares en el espacio tienen especial interés cuando los ángulos determinan la función, como en el caso de la hélice.
n dimensiones[editar]
Es posible generalizar estas ampliaciones de forma que se obtenga un sistema de representación para 4 o más dimensiones. Por ejemplo, para 4 dimensiones se obtiene
Aplicaciones[editar]
Las coordenadas polares son bidimensionales, por lo que solamente se pueden usar donde las posiciones de los puntos se sitúen en un plano bidimensional. Son las más adecuadas en cualquier contexto donde el fenómeno a considerar esté directamente ligado con la dirección y longitud de un punto central, como en las figuras de revolución, en los movimientos giratorios, en las observaciones estelares, etc. Los ejemplos vistos anteriormente muestran la facilidad con la que las coordenadas polares definen curvas como la espiral de Arquímedes, cuya ecuación en coordenadas cartesianas sería mucho más intrincada. Además muchos sistemas físicos, tales como los relacionados con cuerpos que se mueven alrededor de un punto central, o los fenómenos originados desde un punto central, son más simples y más intuitivos de modelar usando coordenadas polares. La motivación inicial de la introducción del sistema polar fue el estudio del movimiento circular y el movimiento orbital.
[editar]
Las coordenadas polares se usan a menudo en navegación, ya que el destino o la dirección del trayecto pueden venir dados por un ángulo y una distancia al objeto considerado. Las aeronaves, por ejemplo, utilizan un sistema de coordenadas polares ligeramente modificado para la navegación.
Modelado[editar]
Los sistemas que representan simetría radial poseen unas características adecuadas para el sistema de coordenadas polares, con el punto central actuando como polo. Un primer ejemplo de este uso es la ecuación del flujo de las aguas subterráneas cuando se aplica a pozos radialmente simétricos. De la misma manera, los sistemas influenciados por una fuerza central son también buenos candidatos para el uso de las coordenadas polares. Algunos ejemplos son las antenas radioeléctricas, o los campos gravitatorios, que obedecen a la ley de la inversa del cuadrado (véase el problema de los dos cuerpos).
Los sistemas radialmente asimétricos también pueden modelarse con coordenadas polares. Por ejemplo la directividad de un micrófono, que caracteriza la sensibilidad del micrófono en función de la dirección del sonido recibido, puede representarse por curvas polares. La curva de un micrófono cardioide estándar, el más común de los micrófonos, tiene por ecuación r = 0,5 + 0,5 sen θ.[13]
Campos escalares[editar]
Un problema en el análisis matemático de funciones de varias variables es la dificultad para probar la existencia de un límite, ya que pueden obtenerse diferentes resultados según la trayectoria de aproximación al punto. En el origen de coordenadas, uno de los puntos que tienen más interés para el análisis (por anular habitualmente funciones racionales o logarítmicas), este problema puede solventarse aplicando coordenadas polares. En otros puntos es posible realizar un cambio de sistema de referencia y así aplicar el truco.
Al sustituir las coordenadas cartesianas x, y, z, …, por sus correspondientes equivalencias en coordenadas polares, el límite al aproximarse al origen se reduce a un límite de una única variable, lo que resulta fácil de calcular por ser el seno y el coseno funciones acotadas y r un infinitésimo. Si el resultado no muestra dependencia angular, es posible aseverar que el límite es indistinto del punto y trayectoria desde el que se ha aproximado.
Véase también[editar]
Referencias[editar]
- ↑ Friendly, Michael. «Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization». Archivado desde el original el 24 de diciembre de 2008. Consultado el 10 de noviembre de 2008.
- ↑ Boyer, C. B. (1949). «Newton as an Originator of Polar Coordinates». American Mathematical Monthly 56. 10.2307/2306162, pags. 73-78.
- ↑ Smith, David Eugene (1925). History of Mathematics, Vol II. Boston: Ginn and Co. pp. 324.
- ↑ «Polar Coordinates and Graphing» (PDF). 13 de abril de 2006. Archivado desde el original el 15 de febrero de 2012. Consultado el 11 de enero de 2009.
- ↑ David Cohen, Theodore Lee; David Sklar (2005). Thomson Brooks/Cole, ed. Precalculus: With Unit-Circle Trigonometry (Cuarta Edición edición). ISBN 0534402305.
- ↑ Ian Stewart; David Tall (1983). Cambridge University Press, ed. Complex Analysis (the Hitchhiker's Guide to the Plane). ISBN 0521287634.
- ↑ Raymond A. Serway; John W. Jewett, Jr. (2005). Brooks/Cole—Thomson Learning, ed. Principles of Physics. ISBN 0-534-49143-X.
- ↑ Claeys, Johan. «Polar coordinates». Archivado desde el original el 27 de abril de 2006. Consultado el 11 de enero de 2009.
- ↑ Smith, Julius O. «Euler's Identity». Mathematics of the Discrete Fourier Transform (DFT). W3K Publishing. ISBN 0-9745607-0-7. Archivado desde el original el 15 de septiembre de 2006. Consultado el 11 de enero de 2009.
- ↑ Husch, Lawrence S. «Areas Bounded by Polar Curves». Archivado desde el original el 1 de marzo de 2000. Consultado el 11 de enero de 2009.
- ↑ Lawrence S. Husch. «Tangent Lines to Polar Graphs». Archivado desde el original el 21 de noviembre de 2019. Consultado el 11 de enero de 2009.
- ↑ Wattenberg, Frank (1997). «Coordenadas esféricas». Archivado desde el original el 22 de diciembre de 2008. Consultado el 26 de noviembre de 2008.
- ↑ Eargle, John (2005). Springer, ed. Handbook of Recording Engineering (Fourth Edition edición). ISBN 0387284702.
Enlaces externos[editar]
 Wikimedia Commons alberga una galería multimedia sobre Coordenadas polares.
Wikimedia Commons alberga una galería multimedia sobre Coordenadas polares.









![{\displaystyle (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)

















































