Sector circular

Sector circular de ángulo θ.

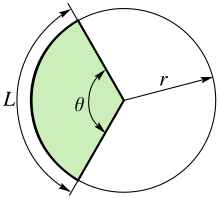
Se denomina sector circular a la porción del círculo determinada por un ángulo central formado por dos radios; Quedando así delimitada por un arco y dos radios.​

Área del sector circular

El área de un sector circular depende las dos líneas rectas al ángulo central, y está dada por las siguientes fórmulas equivalentes:

$A={\frac {r\cdot L}{2}}={\frac {r^{2}\theta }{2}}=\pi r^{2}{\frac {\alpha }{360^{\circ }}}$

Donde

• $r$ es el radio.
• $L$ es la longitud del arco ($0<L<2\pi r$).
• $\theta \,$ es el ángulo central en radianes($L=\theta r$ y $0<\theta <2\pi$).
• $\alpha \,$ corresponde al ángulo $\theta \,$ en grados sexagesimales($0<\alpha <360^{\circ }$).

Demostración

Véase que el área del sector circular es una fracción del área total de un círculo $A_{T}=\pi \cdot r^{2}$ expresada en función de la longitud total del arco $2\pi r$, es decir: $A_{T}={\frac {r}{2}}(2\pi r)$ expresado como $A={\frac {r}{2}}(2\pi r{\frac {\alpha }{360^{\circ }}})$ interpretado como $A=A_{T}{\frac {\alpha }{360^{\circ }}}$ las fracciones de equivalencia son: $0\leq {\frac {\alpha }{360^{\circ }}}={\frac {\theta }{2\pi }}={\frac {L}{2\pi r}}\leq 1$

Longitud del arco

$L={2\pi r\cdot \alpha \over 360^{\circ }}=r\theta$

Véase también

• Cuerda (geometría).
• Segmento circular: la parte del sector comprendida entre el arco y la cuerda.
• Sección cónica.
• Región circular

Enlaces externos

• Definition and properties of a circle sector con animación interactiva
• Weisstein, Eric W. «Sector circular». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 

• Datos: Q203435
• Multimedia: Circular sectors / Q203435