Circunferencia

La circunferencia es una curva plana y cerrada tal que todos sus puntos están a igual distancia del centro.^[1]

Está definida por los infinitos puntos de un plano que distan de un punto fijo (centro) en una magnitud constante denominada radio.

Una circunferencia es el lugar geométrico de los puntos de un plano que equidistan a otro punto llamado centro.

Distíngase de círculo, cuyo lugar geométrico queda determinado por una circunferencia, y la región del plano que encierra esta.

Historia

El interés por conocer la longitud de una circunferencia surge en Babilonia. Cuando usaban los carros con ruedas, era primordial relacionar el diámetro o radio con la circunferencia ayudando a mejorar la precisión a la hora de fabricación de las ruedas y a su vez facilitar el transporte .^[2]

Partes

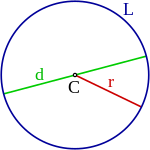
Elementos relevantes de la circunferencia, heredados por el círculo:

El centro es el punto equidistante a todos los puntos de una circunferencia. Señalado con el nombre $C$ en la figura.
Un radio es cualquier segmento que une el centro de la circunferencia con un punto cualquiera de la misma. El radio también es la longitud de los segmentos del mismo nombre. Señalado con el nombre $r$ en la figura.
Un diámetro es cualquier segmento que une dos puntos de la circunferencia pasando por su centro. El diámetro también es la longitud del segmento del mismo nombre. Señalado con el nombre $d$ en la figura.
El perímetro es el contorno de la circunferencia y su longitud. Señalado con el nombre $L$ en la figura.
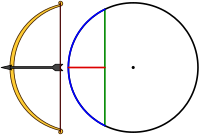
Una cuerda es cualquier segmento que une dos puntos de una circunferencia. El diámetro es una cuerda de máxima longitud. Segmento verde en la figura.
Un arco es cualquier porción de circunferencia delimitada por dos puntos sobre esta. Se dice también que una cuerda subtiende cada arco que determinan sus extremos. Línea curva azul en la figura.
Una flecha o sagita respecto una cuerda es el segmento de su mediatriz que hay entre esta cuerda y el arco que determina esta, sin pasar por el centro. Segmento rojo en la figura.
Una semicircunferencia es cualquier arco delimitado por los extremos de un diámetro.

Perímetro

La longitud de una circunferencia en función del radio $r$ o del diámetro $d=2\cdot r$ es:

\ell =2\pi \cdot r=

\pi \cdot d

donde $\pi =3,14159\dots$ es la constante pi.

Área

Artículo principal: Círculo

El área del círculo o de la región del plano delimitada por una circunferencia:

A =

{\frac {\ell \cdot r}{2}}=

\pi \cdot r^{2}=

{\frac {\pi \cdot d^{2}}{4}}

Propiedades

Solo las rectas que contengan el centro de la circunferencia pueden ser un eje de simetría de esta.
Los puntos de la circunferencia sobre cualquier perpendicular a las recta que pasa por el centro son equidistantes a esta. Al construir un triángulo isósceles con dos radios y la perpendicular queda probado que son equidistantes a la recta que ahora se le puede llamar recta de simetría.

Las circunferencias son invariantes a cualquier rotación con el eje en el centro de esta circunferencia.
Trivial después de entender que los radios sufren una rotación, por tanto, no modifican su longitud ni su origen común, ya que se trata de un desplazamiento del plano y por tanto una isometría.

Posiciones relativas respecto la circunferencia

Véase también: Posiciones relativas en el círculo

Puntos

Posiciones de los puntos respecto de la circunferencia:

Un punto exterior es el que está a una distancia mayor al radio de la circunferencia respecto la posición de su centro.
Un punto interior es el que está a una distancia menor al radio de la circunferencia respecto la posición de su centro.

Rectas

Posiciones de las rectas respecto de la circunferencia:

Una recta exterior es cualquier recta que no tiene puntos en común con la circunferencia.
Una recta tangente es cualquier recta que toca la circunferencia en un único punto.
Una recta secante es cualquier recta que corta la circunferencia en dos puntos.^[3]

Se llama punto de tangencia cada uno de los puntos que comparte la circunferencia con los diferentes elementos tangentes, es decir, el punto donde se produce la tangencia. En todo punto de la circunferencia se pueden hacer tangencias.

Propiedades

Toda recta tangente a una circunferencia es perpendicular al radio que contiene el punto de tangencia.
Por reducción al absurdo, se puede suponer que no es perpendicular, por tanto, se puede construir un triángulo isósceles con otro radio, probando así que hay otro punto de tangencia diferente al primero y como este debería ser único implica la negación de que no sean perpendiculares y por tanto es un ángulo recto.

Entre circunferencias

Posiciones entre circunferencias:

Una circunferencia es exterior a otra, si todos sus puntos son exteriores a esta otra. Véase la figura 1 y 8.
Una circunferencia es interior a otra, si todos sus puntos son interiores a esta otra. Véase la figura 5.
Una circunferencia es circundante a otra, si todos sus puntos no son interiores a esta otra que a su vez no es exterior a la primera. Véase las figuras 7 y 8.
Una circunferencia es tangente exterior a otra, si tienen un único punto común y todos los demás puntos de una son exteriores a la otra. Véase la figura 2.
Una circunferencia circundante es tangente exterior a otra, si tienen un único punto común. Véase la figura 7.
Una circunferencia es tangente interior a otra, si tienen un único punto común y todos los demás puntos de una son interiores a la otra. Véase la figura 4.
Una circunferencia es secante a otra, si se cortan en dos puntos distintos. Véase la figura 3.
Una circunferencia es secante ortogonalmente a otra, si el ángulo de su intersección es recto, es decir, sus rectas tangentes en cada una de las intersecciones son perpendiculares.
Son excéntricas las circunferencias que no tienen el mismo centro.
Son concéntricas las circunferencias que tienen el mismo centro, es decir, las que no son excéntricas.
Son coincidentes las circunferencias que tienen el mismo centro y el mismo radio, es decir, que todos los puntos de una son los de la otra y viceversa. Véase la figura 6.

Propiedades

Los centros de las circunferencias tangentes están alineados con el punto de tangencia.
Como la recta tangente en el punto es perpendicular al radio, implica que todos los radios son perpendiculares a dicha recta tangente en el mismo punto, es decir, todos los centros están alineados.

Ángulos en una circunferencia

Posición de los ángulos respecto de una circunferencia, puede ser:

Un ángulo central es el que tiene su vértice en el centro de la circunferencia.^[4] Véase la figura 1.
Un ángulo inscrito es el que tiene su vértice sobre la circunferencia cuyos lados determinan una cuerdas cada uno en la dicha circunferencia.^[4] Véase la figura 2.
Un ángulo semi-inscrito es el que tiene su vértice sobre la circunferencia y uno de sus lados secantes determina una cuerda y el otro una recta tangente a la circunferencia, es decir, que el vértice es un punto de tangencia.^[4] Véase la figura 3.
Un ángulo ex-inscrito es el que tiene su vértice sobre la circunferencia y uno de sus lados determina una cuerda y la prolongación del otro determina otra cuerda, es decir, es el ángulo exterior de un ángulo inscrito.^[5] Véase la figura 4.
Un ángulo interior es el que tiene su vértice en el interior de la circunferencia.^[4] Véase la figura 5.
Un ángulo exterior es el que tiene su vértice en el exterior de la circunferencia y cada lado es tangente o secante a la circunferencia.^[4] Véanse las figuras 6,7 y 8.

Propiedades

En el ángulo central su amplitud $\alpha$ y el radio $r$ de la circunferencia, determina la longitud del arco $\ell ,$ resaltado en la figura en azul. Si el ángulo está en grados:

$\ell _{\alpha }=$ ${\frac {\alpha }{180^{\circ }}}\cdot \pi \cdot r$
El ángulo central indica qué fracción de circunferencia que tiene el arco, así, si $\ell =2\pi \cdot r=$ entonces: $\ell _{\alpha }={\frac {\alpha }{360^{\circ }}}\cdot 2\pi \cdot r$ Es decir, el arco es directamente proporcional al ángulo central, y que simplificando queda la fórmula buscada.

Si el ángulo está en radianes:

\ell _{\alpha }=

\alpha \cdot r

Artículo principal: Arco capaz

El arco capaz relaciona el ángulo central, inscrito, semi-inscrito y ex-inscrito siempre que las intersecciones de los lados mantengan la misma distancia.

Si el ángulo inscrito, semi-inscrito y ex-inscrito tienen la misma amplitud $\alpha$ , entonces, determinan la misma longitud de arco, de color azul en la imagen, sobre una misma circunferencia de radio $r$ . Si el ángulo está en grados:

$\ell _{\alpha }=$ ${\frac {\alpha }{90^{\circ }}}\cdot \pi \cdot r$
Como el ángulo central mide el doble que el ángulo inscrito, semi-inscrito y ex-inscrito, este hecho se sustituye en la fórmula usada en el ángulo central quedando: $\ell _{\alpha }={\frac {2\cdot \alpha }{360^{\circ }}}\cdot 2\pi \cdot r$ Simplificando queda la fórmula buscada.

Si el ángulo está en radianes:

\ell _{\alpha }=

\alpha \cdot 2\cdot r

Diversos tipos de ángulos aparecen en el análisis de la potencia de un punto respecto de una circunferencia.

Inscripción y circunscripción

Diremos que una circunferencia está circunscrita a un polígono cuando todos los vértices de dicho polígono están sobre esta, se dice que este polígono está inscrito.

Diremos que una circunferencia está inscrita a un polígono cuando sea tangente a todos los lados de dicho polígono, se dice que este polígono está circunscrito.

Construcción con regla y compás

Hay muchas construcciones con regla y compás que resultan en circunferencias.

A partir del centro y un punto de la circunferencia

Esta es la más sencilla. Basta colocar la aguja del compás en el centro de la circunferencia y el otro extremo en el otro punto y girar.

A partir del diámetro

Construye el punto medio $M$ del diámetro.
Construye la circunferencia con centro en $M$ que pasa por los extremos del diámetro como se describe en el apartado anterior.

A partir de tres puntos no alineados

Llama a los puntos $A,B$ y $C$ .
Construye el triángulo $ABC$ construyendo los segmentos $AB,BC$ y $CA$ .
Construye la mediatriz del segmento $AB$ .
Construye la mediatriz del segmento $BC$ .
Encuentra la intersección de estas dos mediatrices (existe porque $A,B$ y $C$ no están alineados) y llámala $M$ . Esta intersección es el circuncentro de $ABC$ y, por tanto, equidista de los tres vértices.
Construye como se describe en el primer apartado la circunferencia con centro $M$ que pasa por alguno de los puntos $A,B$ o $C$ (también pasará por los otros dos por equidistar $M$ de los tres vértices).

Representación de la circunferencia

La circunferencia se puede representar mediante ecuaciones o funciones que determinan la posición de cada uno de sus puntos. Para ello solo hace falta garantizar que la distancia de cada punto $P$ de la circunferencia a su centro $C$ sea constante para cada una de las ecuaciones y funciones que se tenga.

Ecuación de la circunferencia

circunferencia de radio dos en un sistema de coordenadas

Una circunferencia queda determinada por un centro $C=(a,\,b)$ y un radio $r$ , por tanto, su ecuación queda determinada al imponer que la distancia de sus puntos, $P=(x,\,y)$ , al centro sea constante, es decir, $\|P-C\|=r$ dando la siguiente ecuación:^[6]^[7]

(x-a)^{2}+(y-b)^{2}=r^{2}.

Su representación en un sistema de coordenadas viene dada por cada punto de la forma $(x,\,y)$ que satisfacen la ecuación.

La ecuación anterior es más sencilla si está centrada en el origen de coordenadas $C=(0,\,0):$

x^{2}+y^{2}=r^{2}.

La circunferencia de centro en el origen de coordenadas y radio uno se denomina circunferencia unidad o circunferencia goniométrica y su ecuación es:^[8]^[9]^[10]^[11]^[12]

x^{2}+y^{2}=1.

Su función implícita es $f(x,\,y)=x^{2}+y^{2}-1$ y para representar la circunferencia se buscan los puntos del plano que cumplen la ecuación $f(x,\,y)=0.$

Propiedades

Es posible usar cuadratura para hallar la ecuación de la circunferencia a partir de su ecuación extendida:

$x^{2}+y^{2}+Dx+Ey+F=0$
Aplicando cuadratura a $x^{2}+Dx$ y $y^{2}+Ey$ se deduce que: $a=-{\frac {D}{2}}$ $b=-{\frac {E}{2}}$ y por tanto $(x-a)^{2}+(y-b)^{2}=a^{2}+b^{2}-F$ de donde: $r={\sqrt {a^{2}+b^{2}-F}}.$

A partir de los puntos extremos de un diámetro, $(x_{1},y_{1})$ y $(x_{2},y_{2})$ , la ecuación de la circunferencia es:

$(x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})=0.$
Solo hace falta extender el producto de la ecuación dada para identificar la circunferencia: $(x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})=$ $x^{2}-x\cdot x_{1}-x\cdot x_{2}+x_{1}\cdot x_{2}+y^{2}-y\cdot y_{1}-y\cdot y_{2}+y_{1}\cdot y_{2}$ Finalmente se debe observar que los dos puntos anulan la ecuación y probar que el punto medio es el centro.

Función paramétrica

La circunferencia con centro en $C=(a,\,b)$ y radio $r$ se puede parametrizar usando funciones trigonométricas de un solo parámetro $\theta$ para obtener una función paramétrica $r_{C}(\theta )=(x,\,y):$

{\begin{array}{l}x=a+r\,\cos \theta \\y=b+r\,\operatorname {sen} \theta \end{array}}

\theta \in [0,\,2\,\pi )

También se puede parametrizar con funciones funciones racionales como

${\begin{array}{l}x=a+r\left({\frac {1-t^{2}}{1+t^{2}}}\right)\\y=b+r\left({\frac {2t}{1+t^{2}}}\right)\end{array}}$ $t\in {\bar {\mathbb {R} }}$
Primero se utiliza un haz de rectas del tipo $y=ax$ para proyectar los valores de $t$ sobre la recta vertical $x=1$ que serán de la forma $(1,\,t)$ y proyectando serán de la forma $(a,\,a\cdot t)$ . Proyección sobre recta horizontal. Si se sustituye sobre la circunferencia unidad $(x-1)^{2}+y^{2}=1,$ nos dará la intersección de la proyección sobre esta circunferencia y por tanto los puntos de esta paramétricamente: $(a-1)^{2}+(a\cdot t)^{2}=1\Leftrightarrow$ $a^{2}\cdot (1+t^{2})=2\cdot a\Rightarrow$ $a={\frac {2}{1+t^{2}}}$ finalmente sustituyendo sobre el haz y arreglando las fracciones queda $\left({\frac {1-t^{2}}{1+t^{2}}},\,{\frac {2\cdot t}{1+t^{2}}}\right)$

donde ${\bar {\mathbb {R} }}$ incluye el punto en el infinito.^[13]

Función paramétrica en el plano complejo

En el plano complejo, una circunferencia con centro $C=a+i\,b$ y radio $r$ a partir de la ecuación de la circunferencia $|z-c|=r$ se obtiene la forma paramétrica:^[14]^[15]

z=re^{i\theta }+C=

r(\cos \theta +i\operatorname {sen} \theta )+a+i\,b

donde $\theta \in [0,\,2\,\pi ).$

Función vectorial

Como en la función paramétrica, la circunferencia puede representarse en cualquier subespacio de dimensión dos de un espacio vectorial usando dos vectores ortonormales ${\vec {u}}$ y ${\vec {v}}$ , y por tanto generadores de dicho subespacio, permitiendo construir la circunferencia en cualquier plano oblicuo con centro ${\vec {c}}$ y radio $r$ que viene dada o descrita por la función vectorial:

r(\theta )=

{\vec {c}}+{\vec {u}}r\cos \theta +{\vec {v}}r\operatorname {sen} \theta

donde

\theta \in [0,\,2\pi ).

Ecuación en coordenadas polares

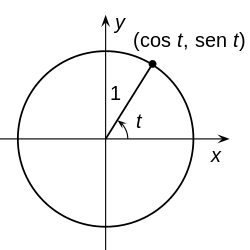
Toda curva plana dada en coordenadas polares es de la forma $\alpha (\theta )=$ $(\rho (\theta )\cos \theta ,\,\rho (\theta )\operatorname {sen} \theta )$ donde $\rho (\theta )$ es la distancia al centro o polo $O$ y $\theta$ el ángulo respecto el eje OX, por tanto la expresión de una circunferencia con centro en el polo y radio $r$ es:

$\alpha (\theta )=$ $(r\cos \theta ,\,r\operatorname {sen} \theta )$
La curva $\alpha (\theta )$ tiene que cumplir la ecuación: $x^{2}+y^{2}=r^{2}.$ Es decir: $(\rho (\theta )\cos \theta )^{2}+(\rho (\theta )\operatorname {sen} \theta )^{2}=r^{2}.$ De donde se deduce que $\rho (\theta )=r$

Cuando el centro está en el punto $(d,0)$ con radio $r$ la circunferencia es:

$\alpha (\theta )=$ $(\rho (\theta )\cos \theta ,\,\rho (\theta )\operatorname {sen} \theta )$ donde $\rho (\theta )=$ $d\cos \theta +{\sqrt {r^{2}-d^{2}\operatorname {sen} \theta }}$
Extendiendo la ecuación de la circunferencia: $(x-d)^{2}+y^{2}=r^{2}\Rightarrow$ $x^{2}-2x\cdot d+d^{2}+y^{2}=r^{2}\Rightarrow$ $x^{2}+y^{2}-2x\cdot d+d^{2}-r^{2}=0.$ Se hace el cambio $x=\rho (\theta )\cos \theta$ y $y=\rho (\theta )\operatorname {sen} \theta$ y se simplifica como: $\rho (\theta )^{2}-2\rho (\theta )d\cos \theta +d^{2}-r^{2}=0\Rightarrow$ $\rho (\theta )=$ $d\cos \theta \pm {\sqrt {r^{2}-d^{2}\operatorname {sen} \theta }}.$ Finalmente se toma la raíz positiva para que $\rho (\theta )>0.$ El polo no puede ser exterior a la circunferencia porque el dominio del parámetro no queda definido continuamente en la parametrización.

Propiedad

Dados tres puntos cualesquiera no alineados $(x_{1},\,y_{1}),\,(x_{2},\,y_{2})$ y $(x_{3},\,y_{3})$ existe una única circunferencia que contiene a estos tres puntos, es decir, esta circunferencia estará circunscrita al triángulo definido por estos puntos. La ecuación de la circunferencia está dada de por el determinante matricial:

\det {\begin{bmatrix}x&y&x^{2}+y^{2}&1\\x_{1}&y_{1}&x_{1}^{2}+y_{1}^{2}&1\\x_{2}&y_{2}&x_{2}^{2}+y_{2}^{2}&1\\x_{3}&y_{3}&x_{3}^{2}+y_{3}^{2}&1\\\end{bmatrix}}=0.

Formas de identificar circunferencias

Según el área que se trabaje, hay formas de identificar y usar una circunferencia implícitamente, además de sus funciones y ecuaciones.

En topología

En topología, se denomina circunferencia a cualquier curva cerrada simple que sea homeomorfa a la circunferencia usual de la geometría (es decir, la esfera 1–dimensional). Se la puede definir como el espacio cociente determinado al identificar como uno los dos extremos de un intervalo cerrado. Sin embargo, los geómetras llaman 2-esfera a la circunferencia, mientras que los topólogos se refieren a ella como 1-esfera y la indican como $S^{1}\,\!$ , dando lugar a posibles confusiones.^[16]

La dimensión de la circunferencia es 1. De igual modo, la dimensión de una recta no acotada, o de un arco — esto es de un conjunto homeomorfo con un intervalo cerrado — y de una curva cerrada simple, i.e. un conjunto homeomorfo con una circunferencia, es igual a 1.^[17] También el caso de una poligonal cerrada.

En ecuaciones diferenciales

En el tema de ecuaciones diferenciales, una circunferencia puede determinarse mediante una curva integral de una ecuación diferencial como:

{\begin{array}{l}x'=-y\\y'=\,x\end{array}}

En geometría diferencial de curvas

En teoría local de la curva, se considera como circunferencia una curva de curvatura constante sin torsión.

Circunferencias particulares

Circunferencias de Cardanus

Un par de circunferencias que se desplazan, tangencial e interiormente, una sobre la otra guardando una razón entre sus radios de 1:2. Investigadas, originalmente, por el matemático italiano, Girolamo de Cardano^[18]

Circunferencia directriz

Usada en una alternativa definitoria de la elipse y de la hipérbola, siendo estas el lugar de los centros de las circunferencias tangentes a la llamada «circunferencia directriz».^[18]

Circunferencia osculatriz

Al tratar de la curvatura de una curva o de una superficie, en el punto de contacto, además de la tangente se toma en cuenta la circunferencia de la curvatura, llamada «circunferencia osculatriz».^[18]^[19]

Véase también

Referencias

↑ Real Academia Española. «Circunferencia». Diccionario de la lengua española (23.ª edición).
↑ Boyer: Historia de la matemática
↑ De forma muy particular y para facilitar explicaciones didácticas en diferentes libros es posible encontrar por recta radial o recta diametral a las rectas que contienen al centro, un diámetro o un radio de una circunferencia.
↑ ^a ^b ^c ^d ^e RACEFN, ed. (1999). Diccionario Esencial de las Ciencias. Editorial Espasa Calpe, S.A. p. 61. ISBN 84-239-7921-0.
↑ Dibujo técnico I Escrito por CÉSAR CALAVERA OPI, ISABEL JIMÉNEZ RUIZ, pg 52
↑ Haaser, La Salle, Sulivan: Análisis Matemático I
↑ Según la especialización del libro consultado, la barra simple o la doble barra vertical representa la distancia, en este caso corresponde a la distancia euclidiana donde la distancia entre dos puntos es $d(P,\,C)=$ $\|P-C\|=$ ${\sqrt {(x-a)^{2}+(y-b)^{2}}}.$
↑ "Introducción a la geometría" Eugenio Roanes Macías. Anaya editorial. 1.ª ed, 1980. ISBN 84-207-1478-X
↑ "Geometría Diferencial" Antonio López de la Rica, Agustín de la Villa Cuenca. 1997. ISBN 84-921847-3-6
↑ "Geometría analítica del plano y del espacio". Jesús M. Ruiz. Anaya, 1.ª ed, 2003. ISBN 84-667-2612-8
↑ "Cálculus" (Volumen I). Tom M. Apostol. Segunda edición, 1991. Editorial Reverté, S.A. ISBN 84-291-5002-1
↑ "Cálculo" (Volumen I) Ron Larson, Robert P. Hostetler, Bruce H. Edwards. McGraw-Hill, Octava edición, 2006. ISBN 970-10-5274-9
↑ Geometría analítica de Pastor, Santaló y Balanzat, página 76.
↑ $e^{z}$ es una función analítica, usada para describir regiones circulares en plano complejo como arcos de circunferencias alrededor de un punto, por tanto, frecuente en diversa bibliografía de análisis.
↑ Weinberger, Hans F. (1992). Ecuaciones diferenciales en derivadas parciales (Dr. D. Francisco Vélez Cantarell, trad.) [Partial differential equations]. Ed Reverté, S.A. pp. a partir de la gágina 215. ISBN 84-291-5160-5.
↑ Weisstein, Eric W. «Circle». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. Consultado el 2016.
↑ Kazimierz Kuratowski: Introducción a la teoría de conjuntos y a la topología, Editorial Vicens Vives, Barcelona, España, 1966
↑ ^a ^b ^c Diccionarios RIODUERO. Matemáticas. ISBN 84-220-0832-7
↑ Cf. Barrett O'Neill. Elementos de Geometría Diferencial pág. 80 Limusa Wiley

Enlaces externos

Wikimedia Commons alberga una categoría multimedia sobre círculos y circunferencias.
Wikiversidad alberga proyectos de aprendizaje sobre Circunferencia.
Ejercicios resueltos y video tutoriales sobre la circunferencia
Círculo y circunferencia, en Descartes. Centro Nacional de Información y Comunicación Educativa. Ministerio de Educación, Política Social y Deporte de España
Materiales didácticos: Circunferencia, en Descartes
Círculo y circunferencia en webdelprofesor.ula.ve, de la Universidad de Los Andes, Venezuela
Weisstein, Eric W. «Circunferencia "Circumference"». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.

Datos: Q843905

[1] Real Academia Española. «Circunferencia». Diccionario de la lengua española (23.ª edición).

[2] Boyer: Historia de la matemática

[3] De forma muy particular y para facilitar explicaciones didácticas en diferentes libros es posible encontrar por recta radial o recta diametral a las rectas que contienen al centro, un diámetro o un radio de una circunferencia.

[RAC-4] RACEFN, ed. (1999). Diccionario Esencial de las Ciencias. Editorial Espasa Calpe, S.A. p. 61. ISBN 84-239-7921-0.

[5] Dibujo técnico I Escrito por CÉSAR CALAVERA OPI, ISABEL JIMÉNEZ RUIZ, pg 52

[6] Haaser, La Salle, Sulivan: Análisis Matemático I

[7] Según la especialización del libro consultado, la barra simple o la doble barra vertical representa la distancia, en este caso corresponde a la distancia euclidiana donde la distancia entre dos puntos es $d(P,\,C)=$ $\|P-C\|=$ ${\sqrt {(x-a)^{2}+(y-b)^{2}}}.$

[8] "Introducción a la geometría" Eugenio Roanes Macías. Anaya editorial. 1.ª ed, 1980. ISBN 84-207-1478-X

[9] "Geometría Diferencial" Antonio López de la Rica, Agustín de la Villa Cuenca. 1997. ISBN 84-921847-3-6

[10] "Geometría analítica del plano y del espacio". Jesús M. Ruiz. Anaya, 1.ª ed, 2003. ISBN 84-667-2612-8

[11] "Cálculus" (Volumen I). Tom M. Apostol. Segunda edición, 1991. Editorial Reverté, S.A. ISBN 84-291-5002-1

[12] "Cálculo" (Volumen I) Ron Larson, Robert P. Hostetler, Bruce H. Edwards. McGraw-Hill, Octava edición, 2006. ISBN 970-10-5274-9

[13] Geometría analítica de Pastor, Santaló y Balanzat, página 76.

[14] $e^{z}$ es una función analítica, usada para describir regiones circulares en plano complejo como arcos de circunferencias alrededor de un punto, por tanto, frecuente en diversa bibliografía de análisis.

[15] Weinberger, Hans F. (1992). Ecuaciones diferenciales en derivadas parciales (Dr. D. Francisco Vélez Cantarell, trad.) [Partial differential equations]. Ed Reverté, S.A. pp. a partir de la gágina 215. ISBN 84-291-5160-5.

[16] Weisstein, Eric W. «Circle». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. Consultado el 2016.

[17] Kazimierz Kuratowski: Introducción a la teoría de conjuntos y a la topología, Editorial Vicens Vives, Barcelona, España, 1966

[Diccionarios_RIODUERO_1-18] Diccionarios RIODUERO. Matemáticas. ISBN 84-220-0832-7

[19] Cf. Barrett O'Neill. Elementos de Geometría Diferencial pág. 80 Limusa Wiley

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]