Punto (geometría)
El punto en la geometría es uno de los entes fundamentales de la geometría, junto con la recta y el plano, pues son considerados conceptos primarios, es decir, que solo es posible describirlos en relación con otros elementos similares o parecidos[1]. El punto carece de largo, espesor o grosor.[2] Se suelen describir apoyándose en los postulados característicos, que determinan las relaciones entre los entes geométricos fundamentales. El punto es la unidad más simple, irreductiblemente mínima, de la comunicación visual;[3] es una figura geométrica sin dimensión, tampoco tiene longitud, área, volumen, ni otro ángulo dimensional. No es un objeto físico. Describe una posición en el plano, determinada respecto de un sistema de coordenadas preestablecidas[4].
Historia[editar]
El concepto de punto como ente geométrico surge en la antigua concepción griega de la geometría compilada en Alejandría por Euclides en su tratado Los Elementos, dando una definición de punto excluyente: «lo que no tiene ninguna parte». El punto, en la geometría clásica, se basa en la idea de que era un concepto intuitivo, el ente geométrico «sin dimensiones» y solo era necesario asumir la noción de punto.[5]
Representación gráfica[editar]
En algunos textos de geometría se suele utilizar una pequeña cruz (+), círculo (o), cuadrado o triángulo. Con relación a otras figuras, suele representarse con un pequeño segmento perpendicular cuando pertenece a una recta, semirrecta o segmento.
A los puntos se les suele nombrar con una letra mayúscula: A, B, C, etc. (a las rectas con letras minúsculas, y a los ángulos con letras griegas).
La forma de representar un punto mediante dos segmentos que se cortan (una pequeña “cruz” +) presupone que el punto es la intersección. Cuando se representa con un pequeño círculo, circunferencia u otra figura geométrica, presupone que el punto es su centro.
Determinación geométrica[editar]
Un punto puede determinarse con diversos sistemas de referencia:
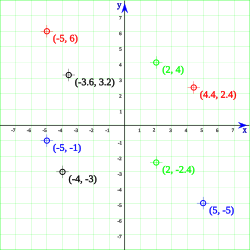
En el sistema de coordenadas cartesianas, se determina mediante las distancias ortogonales a los ejes principales, que se indican con dos letras o números: (x, y) en el plano; y con tres en el espacio (x, y, z).
En coordenadas polares, mediante su distancia al centro y la medida angular respecto del eje de referencia: (r, θ).
En coordenadas esféricas, mediante su distancia al centro y la medida angular respecto de los ejes de referencia: (r, θ, φ).
En coordenadas cilíndricas, mediante coordenadas radial, acimutal y altura: (u, φ, z).
También se pueden emplear sistemas de coordenadas elípticas, parabólicas, esferoidales, toridales, etc.
Dimensión de un punto[editar]
Hay varias definiciones no equivalentes de dimensión en matemáticas. En todas las definiciones comunes, un punto es de dimensión 0.
Dimensión del espacio vectorial[editar]
La dimensión de un espacio vectorial es el tamaño máximo de un subconjunto linealmente independiente. En un espacio vectorial que consiste en un solo punto (que debe ser el vector cero 0), no hay ningún subconjunto linealmente independiente. El vector cero no es en sí mismo linealmente independiente, porque hay una combinación lineal no trivial que lo hace cero: .
Dimensión topológica[editar]
La dimensión topológica de un espacio topológico se define como el valor mínimo de n, tal que toda cobertura abierta finita de admite una cubierta abierta finita de que refina en la que ningún punto esté incluido en más de n+1 elementos. Si no existe tal mínimo n, se dice que el espacio es de dimensión de cobertura infinita.[6]
Un punto es cero dimensional con respecto a la dimensión que lo cubre porque cada cobertura abierta del espacio posee un refinamiento consistente en un conjunto abierto.
Dimensión de Hausdorff[editar]
Sea X un espacio métrico. Si S ⊂ X y d ∈ [0, ∞), el contenido de Hausdorff-dimensional d de S es el infimum del conjunto de números δ ≥ 0 tal que hay alguna colección (indexada) de bolas cubriendo S con ri: > 0 para cada i ∈ I que satisface
La dimensión de Hausdorff de X está definida por
Un punto tiene dimensión de Hausdorff 0 porque puede ser cubierto por una sola bola de radio arbitrariamente pequeño.
Puntos, rectas y planos: posiciones relativas[editar]
Dados tres o más puntos en el plano o en el espacio (según corresponda), se pueden dividir en conjuntos que cumplan o no con las siguientes condiciones. Colineales: los denominados colineales son aquellos contenidos en una recta. Coplanarios: se denominan puntos coplanarios aquellos que están contenidos en un mismo plano.[7]
Algunos postulados y teoremas relacionados con el punto[editar]
- Postulados en geometría euclidiana
- Por un punto pasan infinitas rectas y planos.
- Dos puntos determinan una recta y solo una.
- Una recta contiene infinitos puntos.
- Un plano contiene infinitos puntos e infinitas rectas.
- El espacio contiene infinitos puntos, rectas y planos.
Estos postulados se pueden generalizar para espacios de n dimensiones.
- Teoremas en geometría euclidiana
- Tres puntos no alineados determinan un plano y solo uno.
Masa puntual y función delta de Dirac[editar]
A menudo, en física y matemáticas, es útil imaginar que tiene una masa o carga distinta de cero (esto es especialmente común en el electromagnetismo, donde los electrones se idealizan como puntos con carga distinta de cero). La función delta de Dirac, o función δ, es una función generalizada (informalmente) de la recta numérica real que es cero en todas partes excepto en cero, con una integral de uno en toda la recta real.[8][9][10] La función delta a veces se considera como un pico infinitamente alto e infinitamente delgado en la fuente, con un área total de uno debajo del pico, y representa físicamente una masa puntual idealizada o una carga puntual.[11] Fue publicado por primera vez por el físico teórico Paul Dirac. En el contexto del procesamiento de señales , a menudo se lo denomina símbolo (o función) de impulso unitario.[12] Su análogo discreto es la función delta de Kronecker, que a menudo se define en un dominio limitado y toma los valores 0 y 1.
Véase también[editar]
- Punto medio
- Punto del infinito
- Punto fijo
- Vértice (geometría)
- Recta
- Plano
- Figura geométrica
- Postulados característicos
Referencias[editar]
- ↑ Ohmer, Merlin M. (1969). Elementary Geometry for Teachers. Reading: Addison-Wesley. p. 34–37. OCLC 00218666. (requiere registro).
- ↑ Ohmer, Merlin M. (1969). Elementary Geometry for Teachers. Reading: Addison-Wesley. p. 34–37. OCLC 00218666. (requiere registro).
- ↑ Dondis, A. Donis (2011). La sintaxis de la imagen. Introducción al alfabeto visual. Gustavo Gili. p. 55.
- ↑ Karl Menger, General Spaces and Cartesian Spaces, (1926) Communications to the Amsterdam Academy of Sciences. English translation reprinted in Classics on Fractals, Gerald A.Edgar, editor, Addison-Wesley (1993) ISBN 0-201-58701-7
- ↑ E. Szpilrajn (1937). «La dimension et la mesure». Fundamenta Mathematicae 28: 81-9.
- ↑ V. V. Fedorchuk, The Fundamentals of Dimension Theory, appearing in Encyclopaedia of Mathematical Sciences, Volume 17, General Topology I, (1993) A. V. Arkhangel'skii and L. S. Pontryagin (Eds.), Springer-Verlag, Berlin ISBN 3-540-18178-4.
- ↑ Dirac, Paul (1930), The Principles of Quantum Mechanics (1st edición), Oxford University Press..
- ↑ Dirac, 1958, §15 The δ function
- ↑ Gel'fand y Shilov, 1968, Volume I, §§1.1, 1.3
- ↑ Schwartz, 1950, p. 3
- ↑ Arfken y Weber, 2000, p. 84
- ↑ Bracewell, 1986, Chapter 5
Bibliografía[editar]
- Clarke, Bowman, 1985, "Individuals and Points," Notre Dame Journal of Formal Logic 26: 61–75.
- De Laguna, T., 1922, "Point, line and surface as sets of solids," The Journal of Philosophy 19: 449–61.
- Gerla, G., 1995, "Pointless Geometries" in Buekenhout, F., Kantor, W. eds., Handbook of incidence geometry: buildings and foundations. North-Holland: 1015–31.
- Whitehead, A. N., 1919. An Enquiry Concerning the Principles of Natural Knowledge. Cambridge Univ. Press. 2nd ed., 1925.
- Munkres, James R. (2000). Topology (2nd edición). Prentice-Hall. ISBN 0-13-181629-2.
- Karl Menger, Dimensionstheorie, (1928) B.G Teubner Publishers, Leipzig.
- A. R. Pears, Dimension Theory of General Spaces, (1975) Cambridge University Press. ISBN 0-521-20515-8
- Gannon, Terry (2006), Moonshine beyond the Monster: The Bridge Connecting Algebra, Modular Forms and Physics, ISBN 0-521-83531-3.
- Dodson, M. Maurice; Kristensen, Simon (12. 6. 2003.). «Hausdorff Dimension and Diophantine Approximation». Fractal Geometry and Applications: A Jubilee of Benoît Mandelbrot. Proceedings of Symposia in Pure Mathematics 72 (1). pp. 305-347. Bibcode:2003math......5399D. ISBN 9780821836378. S2CID 119613948. arXiv:math/0305399. doi:10.1090/pspum/072.1/2112110.
- Marstrand, J. M. (1954). «The dimension of cartesian product sets». Proc. Cambridge Philos. Soc. 50 (3): 198-202. Bibcode:1954PCPS...50..198M. doi:10.1017/S0305004100029236.
- Mattila, Pertti (1995). Geometry of sets and measures in Euclidean spaces. Cambridge University Press. ISBN 978-0-521-65595-8.
- Arfken, G. B.; Weber, H. J. (2000), Mathematical Methods for Physicists (5th edición), Boston, Massachusetts: Academic Press, ISBN 978-0-12-059825-0.
Enlaces externos[editar]
 Wikimedia Commons alberga una categoría multimedia sobre punto.
Wikimedia Commons alberga una categoría multimedia sobre punto.- Weisstein, Eric W. «Point». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Point-free geometry, en planetmath.org







