Simetría
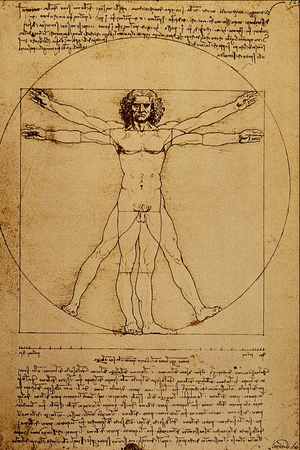
La simetría (del griego őύν "con" y μέτροv "medida") es un rasgo característico de formas geométricas, sistemas, ecuaciones y otros objetos materiales, o entidades abstractas, relacionada con su invariancia bajo ciertas transformaciones, movimientos o intercambios.
Existen cinco tipos de simetría claramente establecidos:
- De rotación. Es el giro que experimenta todo motivo de manera repetitiva hasta que finaliza consiguiendo la posición idéntica que tenía al principio.
- De abatimiento. En este caso lo que se logra es dos partes iguales de un objeto concreto tras llevarse a cabo un giro de 180° de una con respecto a la otra.
- De traslación. Este es el término que se utiliza para referirse al conjunto de repeticiones que lleva a cabo un objeto a una distancia siempre idéntica del eje y durante una línea que puede estar colocada en cualquier posición.
- De ampliación. Se emplea para dejar patente que dos partes de un todo son semejantes y es que tienen la misma forma pero no un tamaño igual.
- Bilateral. Es la que permite que se obtenga un retrato bilateral que tiene como espina dorsal un eje de simetría. A los lados de este aparecen formas iguales a la misma distancia de él que serán las que permitan crear ese citado retrato.
En condiciones formales, un objeto es simétrico en lo que concierne a una operación matemática si el resultado de aplicar esa operación o transformación al objeto, el resultado es un objeto indistinguible en su aspecto del objeto original. Dos objetos son simétricos uno al otro en lo que concierne a un grupo dado de operaciones si uno es obtenido de otro por algunas operaciones (y viceversa). En la geometría 2D las clases principales de simetría de interés son las que conciernen a las isometrías de un espacio euclídeo: traslación, rotaciones, reflexiones y reflexiones que se deslizan. Además de simetrías geométricas existen simetrías abstractas relacionadas con operaciones abstractas como la permutación de partes de un objeto.
En matemática[editar]
En geometría[editar]

Cuando hablamos de objetos físicos o elementos geométricos el concepto de simetría está asociado a transformaciones geométricas tales como las rotaciones, las reflexiones o las traslaciones. Dos simetrías sencillas son la simetría axial y la simetría central. Así se dice que un objeto presenta:
- Simetría esférica si existe simetría bajo cualquier rotación, matemáticamente equivale a que el grupo de simetría de un objeto físico o entidad matemática sea SO(3).
- Simetría cilíndrica o simetría axial si existe un eje tal que los giros alrededor de él no conducen a cambios de posición en el espacio, matemáticamente está asociado a un grupo de isometría SO(2).
- Simetría reflectiva o simetría especular que se caracteriza por la existencia de un único plano, matemáticamente está asociado al grupo O(1) o su representación equivalente . En dos dimensiones tiene un eje de simetría y en tres dimensiones tiene un plano. El eje de simetría de una figura bidimensional es una línea, si se construye una perpendicular, cualquier punto que reposee en esta perpendicular a la misma distancia del eje de simetría son idénticos. Otra manera de verlo es que si la forma se doblara por la mitad sobre el eje, las dos mitades serían iguales. Por ejemplo, un cuadrado tiene cuatro ejes de simetría, ya que hay cuatro formas diferentes de doblarlo haciendo que sus bordes coincidan. Un círculo tendría infinitos ejes de simetría por la misma razón.
- Simetría traslacional se da cuando la transformación deja invariable a un objeto bajo un grupo de traslaciones discretas o continuas. El grupo es discreto si la invariancia solo se da para un número numerable de valores de a y continuo si la invariancia se presenta para un conjunto infinito no numerable de valores de a en caso contrario.
Algunos tipos de simetría que combinan dos o más de los anteriores tipos son:
- Simetría antitraslacional que implica una reflexión en una línea o plano combinado con una traslación a lo largo de ese mismo eje. El grupo de simetría es isomorfo a .
- Simetría de rotorreflexión o simetría de rotación impropia, implica rotación alrededor de un eje combinado con reflexión en un eje perpendicular al de rotación.
- Simetría helicoidal implica un movimiento de rotación en torno a un eje dado con un movimiento de traslación a lo largo de ese mismo eje. Puede ser de tres clases:
- Simetría helicoidal infinita
- Simetría helicoidal de n-ejes
- Simetría helicoidal que no se repite
En lógica[editar]
Una relación binaria R = S × S es simétrica si para cada elemento a, b en S, siempre que sea cierto que Rab, también será cierto Rba.[1] Por lo tanto, la relación «tiene la misma edad que» es simétrica, porque si Pablo tiene la misma edad que María, entonces María tiene la misma edad que Pablo.
En lógica proposicional, las conectivas lógicas binarias simétricas incluyen y (∧, o &), o (∨, o |) y si y solo si (↔), mientras que la conectiva si (→) no es simétrica.[2] Otras conectivas lógicas simétricas incluyen no y (no-y, o ⊼), xor (no-bicondicional, o ⊻) y ni (no-o, o ⊽).
Otras áreas de las matemáticas[editar]
Se puede decir que un objeto matemático es simétrico con respecto a una operación matemática dada, si, cuando se aplica al objeto, esta operación conserva alguna propiedad del objeto.[3] El conjunto de operaciones que preservan una propiedad dada del objeto forman un grupo.
En general, todo tipo de estructura en matemáticas tendrá su propio tipo de simetría. Los ejemplos incluyen funciones pares e impares en cálculo, grupos simétricos en álgebra abstracta, matrices simétricas en álgebra lineal,[4] y grupos de Galois en la teoría de Galois. En estadística, la simetría también se manifiesta como distribuciones de probabilidad simétricas y como asimetría, la asimetría de distribuciones.[5]
En el arte[editar]

En arquitectura[editar]
La simetría se encuentra en la arquitectura en todas las escalas, desde las vistas externas generales de edificios como las catedrales góticas y la Casa Blanca, pasando por el diseño de los plantas y hasta el diseño de elementos de construcción individuales como mosaicos de baldosas. Los edificios islámicos como el Taj Mahal y la mezquita de Lotfollah hacen un uso elaborado de la simetría tanto en su estructura como en su ornamentación.[6][7] Los edificios moriscos como la Alhambra están ornamentados con patrones complejos realizados utilizando simetrías de traslación y reflexión, así como rotaciones.[8]
La arquitectura modernista, comenzando con el estilo internacional, se basa en cambio en «alas y equilibrio de masas».[9]
En dibujo[editar]
En dibujo existen cinco simetrías importantes que son simetría de traslación, rotación, ampliación, bilateral, abatimiento.
- Simetría de traslación o invariancia traslacional es la repetición de una forma a lo largo de una línea en cualquier posición, vertical, horizontal, diagonal o curva, que se desplaza a cualquier distancia constante sobre el eje.
- Simetría de rotación giro de un motivo que se repite cierto número de veces hasta ser idéntico al inicio, tiene determinado orden en la rotación (15°, 30°, 45°, 60°, 90°, hasta 360°). La forma gira en torno a un centro que puede estar dentro de la misma.
- Simetría de ampliación, las partes de él son semejantes, pues tienen la misma forma pero no el mismo tamaño, ya que se extiende del centro hacia afuera para ser cada vez mayor.
- Simetría de abatimiento El eje de giro nos muestra dos partes idénticas con un giro de 180° una en relación con la otra.
- Simetría bilateral Un retrato bilateral, está compuesto por formas iguales a igual distancia a ambos lados de un eje. Todo eso dentro de un eje de simetría.
En alfombras y tapetes[editar]
Una larga tradición del uso de la simetría en alfombras abarca una variedad de culturas. Los indios navajos estadounidenses usaban diagonales en negrita y motivos rectangulares. Muchas alfombras orientales tienen intrincados centros y bordes reflejados que traducen un patrón. No es sorprendente que las alfombras rectangulares tengan típicamente las simetrías de un rectángulo, es decir, motivos que se reflejan tanto en el eje horizontal como en el vertical.[10][11]
En quilts[editar]
Como los quilts están hechas de bloques cuadrados (generalmente 9, 16 o 25 piezas por bloque) y cada pieza más pequeña generalmente consiste en triángulos de tela, la artesanía se presta fácilmente a la aplicación de la simetría.[12]
En otras artes y oficios[editar]

Aparecen simetrías en el diseño de objetos de todo tipo. Los ejemplos incluyen abalorios, muebles, pinturas de arena, nudos, máscaras e instrumentos musicales. Las simetrías son fundamentales para el arte de M. C. Escher y las muchas aplicaciones del mosaico en formas de arte y artesanía como papel tapiz, azulejos de cerámica como en la decoración geométrica islámica, batik, ikat, fabricación de alfombras y muchos tipos de patrones textiles y bordados.[13]
La simetría también se utiliza en el diseño de logotipos.[14] Al crear un logotipo en una cuadrícula y utilizar la teoría de la simetría, los diseñadores pueden organizar su trabajo, crear un diseño simétrico o asimétrico, determinar el espacio entre letras, determinar cuánto espacio negativo se requiere en el diseño y cómo acentuar partes del logo para que se destaque.
En estética[editar]
La relación de la simetría con la estética es compleja. Los seres humanos encuentran la simetría bilateral en los rostros físicamente atractivos;[15] indica salud y aptitud genética.[16][17] A esto se opone la tendencia a que la simetría excesiva se perciba como aburrida o poco interesante. La gente prefiere formas que tengan algo de simetría, pero con la complejidad suficiente para hacerlas interesantes.[18]
En literatura[editar]
La simetría se puede encontrar en varias formas en la literatura, un ejemplo simple es el palíndromo donde un texto breve lee lo mismo hacia adelante o hacia atrás. Las historias pueden tener una estructura simétrica, como en el patrón de subida/bajada de Beowulf.[19]
En física[editar]
En física el concepto de simetría puede formularse en una forma no geométrica. Si K es un conjunto de objetos matemáticos del mismo tipo (funciones, formas geométricas, ecuaciones, ...) que representan algunas propiedades de un sistema físico y G es un grupo de transformaciones que actúa sobre K de tal manera que:
Se dice que un elemento presenta simetría si:[20]
Así por ejemplo varias leyes de conservación de la física son consecuencia de la existencia de simetrías abstractas del lagrangiano, tal como muestra el teorema de Noether. En ese caso K representaría el conjunto de lagrangianos admisibles, k0 el lagrangiano del sistema bajo estudio y G puede representar traslaciones espaciales (conservación del momento lineal), traslaciones temporales (conservación de la energía), rotaciones (conservación del momento angular) u otro tipo de simetrías abstractas (conservación de la carga eléctrica, el número leptónico, la paridad, etc.)
- Ejemplo 1. Como primer ejemplo consideremos un electrón moviéndose entre dos placas infinitas cargadas uniformemente (dicho sistema se aproxima cierto tipo de condensadores), dado que cualquier traslación paralela a los planos constituye una simetría del sistema físico, entonces tanto la fuerza paralela a dichos planos es nula y por tanto la velocidad paralela a los planos es constante.
- Ejemplo 2. Consideremos un satélite orbitando alrededor de un astro (planeta o estrella) con simetría esférica perfecta, consideremos además que la velocidad del satélite sea perpendicular a la línea entre el centro del satélite y el astro. En ese caso, el lagrangiano es totalmente invariante respecto a rotaciones según un eje que pase por el centro de la fuente del campo gravitatorio. En este caso debido a la simetría de rotación tanto del lagrangiano como de las condiciones iniciales del movimiento, la velocidad perpendicular al planeta es constante y la trayectoria es un círculo invariante bajo una rotación perpendicular al plano de la órbita.
Estos dos ejemplos anteriores son casos del teorema de Noether, un resultado general que establece que si existe un grupo uniparamétrico de simetría G para el lagrangiano tal que:
Entonces la cantidad escalar:
Siendo v el campo vectorial que general el grupo uniparamétrico de transformaciones de simetría, y pi los momentos conjugados de las coordenadas generalizadas de posición.
En química[editar]
La simetría es importante para la química (en particular en la química orgánica) porque sustenta esencialmente todas las interacciones específicas entre moléculas en la naturaleza (es decir, a través de la interacción de moléculas quirales naturales y artificiales con sistemas biológicos inherentemente quirales). El control de la simetría de las moléculas producidas en la síntesis química moderna contribuye a la capacidad de los científicos para ofrecer intervenciones terapéuticas con efectos secundarios mínimos. Una comprensión rigurosa de la simetría explica las observaciones fundamentales en química cuántica y en las áreas aplicadas de espectroscopia y cristalografía. La teoría y aplicación de la simetría a estas áreas de la ciencia física se basa en gran medida en el área matemática de la teoría de grupos.[21] Además, el momento dipolar pueden predecirse o ser explicadas a partir de la simetría de la molécula.
Las simetrías que aparecen en química están asociadas a grupos finitos de isometrías, en concreto son grupos puntuales de transformaciones de isometría.
En biología[editar]

Simetría en biología es la equilibrada distribución en el cuerpo de los organismos de aquellas partes que aparecen duplicadas. Los planes corporales de la mayoría de organismos pluricelulares exhiben alguna forma de simetría, bien sea simetría radial o simetría bilateral. Una pequeña minoría no presenta ningún tipo de simetría (son asimétricos).
Simetría radial[editar]
La simetría radial es la simetría definida por un eje heteropolar (distinto en sus dos extremos). El extremo que contiene la boca se llama lado oral, y su opuesto lado aboral o abactinal. Sobre este eje, se establecen planos principales de simetría; dos perpendiculares que definen las posiciones per-radiales. Las estructuras en otros planos (bisectrices de los per-radiales) quedan en posiciones inter-radiales. La zona entre los per-radiales y los inter-radiales es la zona ad-radial
Simetría bilateral[editar]

La mayoría de especies animales tiene simetría bilateral y pertenece por tanto al grupo Bilateria, aunque hay especies como los erizos y las estrellas de mar, que presentan simetría radial secundaria (las fases de desarrollo tempranas y las larvas poseen simetría bilateral que posteriormente se pierde en el adulto).
La simetría bilateral permite la definición de un eje corporal en la dirección del movimiento, lo que favorece la formación de un sistema nervioso centralizado y la cefalización...
En psicología y neurociencia[editar]
Para un observador humano, algunos tipos de simetría son más sobresalientes que otros, en particular el más sobresaliente es un reflejo con un eje vertical, como el presente en el rostro humano. Ernst Mach hizo esta observación en su libro «El análisis de las sensaciones»,[22] y esto implica que la percepción de simetría no es una respuesta general a todo tipo de regularidades. Tanto los estudios conductuales como los neurofisiológicos han confirmado la sensibilidad especial a la simetría de reflexión en humanos y también en otros animales.[23] Los primeros estudios dentro de la tradición Gestalt sugirieron que la simetría bilateral era uno de los factores clave en la agrupación perceptiva. Esto se conoce como principio de simetría. El papel de la simetría en la agrupación y la organización figura / suelo ha sido confirmado en muchos estudios. Por ejemplo, la detección de la simetría de reflexión es más rápida cuando esta es una propiedad de un solo objeto.[24] Los estudios de percepción humana y psicofísica han demostrado que la detección de simetría es rápida, eficiente y robusta a las perturbaciones. Por ejemplo, la simetría se puede detectar con presentaciones entre 100 y 150 milisegundos.[25]
Estudios de neuroimagen más recientes han documentado qué regiones del cerebro están activas durante la percepción de la simetría. Sasaki y otros[26] utilizaron imágenes de resonancia magnética funcional (fMRI) para comparar las respuestas de patrones con puntos simétricos o aleatorios. Hubo una fuerte actividad en las regiones extraestriadas de la corteza occipital, pero no en la corteza visual primaria. Las regiones extraestriadas incluyeron V3A, V4, V7 y el complejo occipital lateral (LOC). Los estudios electrofisiológicos han encontrado una negatividad posterior tardía que se origina en las mismas áreas.[27] En general, una gran parte del sistema visual parece estar involucrado en el procesamiento de la simetría visual, y estas áreas involucran redes similares a las responsables de detectar y reconocer objetos.[28]
En música[editar]
En música clásica, existen composiciones en las que podemos encontrar distribuciones de las notas generadas mediante simetría bilateral, traslación o giros de media vuelta. Algunos ejemplos de composiciones, son: el Preludio de Johann Sebastian Bach, la Sonata en Sol mayor de Domenico Scarlatti, Lotosblume de Robert Schumann, o Die Meistersinger de Richard Wagner.
Estructuras de tono[editar]
La simetría también es una consideración importante en la formación de escalas y acordes, ya que la música tradicional o tonal está formada por grupos de tonos no simétricos, como la escala diatónica o el acorde mayor. Se dice que las escalas o acordes simétricos, como la escala de tonos enteros, el acorde aumentado o el acorde de séptima disminuida, carecen de dirección o sentido de movimiento hacia adelante, son ambiguas en cuanto a la tonalidad o el centro tonal, y tienen una funcionalidad diatónica menos específica. Sin embargo, compositores como Alban Berg, Béla Bartók y George Perle han utilizado ejes de simetría y/o ciclos de intervalo de forma análoga a las claves o centros tonales no tonales.[29]
Los ciclos de intervalo son simétricos y, por lo tanto, no diatónicos. Sin embargo, un segmento de siete tonos de Do5 (el ciclo de quintas, que son enarmónicos con el ciclo de cuartas) producirá la escala diatónica mayor. Las progresiones tonales cíclicas en las obras de compositores románticos como Gustav Mahler y Richard Wagner forman un vínculo con las sucesiones tonales cíclicas en la música atonal de modernistas como Bartók, Alexander Scriabin, Edgard Varèse y la escuela de Viena. Al mismo tiempo, estas progresiones señalan el final de la tonalidad.[29][30]
La primera composición extendida basada consistentemente en relaciones tonales simétricas fue probablemente el Cuarteto de Alban Berg, op. 3 (1910).[30]
En alimentación de corriente alterna[editar]
En el contexto de la electrónica de radiofrecuencia, se habla de una alimentación simétrica de corriente alterna cuando ninguno de los conductores está a la masa. Cuando uno de los conductores está a la masa y el otro experimenta las variaciones de tensión, se dice que la alimentación es asimétrica.
Existen importantes aplicaciones tecnológicas basadas en la alimentación simétrica, ya que la alimentación simétrica tiene la gran ventaja de que la pérdida de potencia en la línea de transmisión es un orden de magnitud menor que la alimentación asimétrica por cable coaxial.
- En efecto, el campo alterno generado por el conductor ascendente es cancelado por el campo generado por su homólogo descendente.
- Además, la alimentación simétrica en delta permite la simplificación de la construcción.
La alimentación simétrica es por lo tanto la alimentación preferida en la operación QRP y en el modo EME, modos donde cada dB de ganancia cuenta.
Véase también[editar]
En estadística[editar]
En juegos y puzles[editar]
En literatura[editar]
Sobre simetría moral[editar]
En física[editar]
- Chen Ning Yang
- Izquierda y derecha en el Cosmos, libro de divulgación científica de Martin Gardner
- Ruptura espontánea de simetría electrodébil
Otros[editar]
- Asimetría
- Maurits Cornelis Escher
- Gödel, Escher, Bach: un Eterno y Grácil Bucle y Yo soy un extraño bucle, de Douglas Hofstadter
- Paridad de una función
- Relación simétrica
Referencias[editar]
- ↑ Josiah Royce, Ignas K. Skrupskelis (2005) The Basic Writings of Josiah Royce: Logic, loyalty, and community (Google eBook) Fordham Univ Press, p. 790
- ↑ Gao, Alice (2019). «Propositional Logic: Introduction and Syntax». University of Waterloo — School of Computer Science. Consultado el 12 de noviembre de 2019.
- ↑ Christopher G. Morris (1992) Academic Press Dictionary of Science and Technology Gulf Professional Publishing
- ↑ «The Definitive Glossary of Higher Mathematical Jargon — Invariance». Math Vault (en inglés estadounidense). 1 de agosto de 2019. Consultado el 12 de noviembre de 2019.
- ↑ Petitjean, M. (2003). «Chirality and Symmetry Measures: A Transdisciplinary Review». Entropy 5 (3): 271-312 (see section 2.9). Bibcode:2003Entrp...5..271P. doi:10.3390/e5030271.
- ↑ Williams: Symmetry in Architecture. Members.tripod.com (1998-12-31). Retrieved on 2013-04-16.
- ↑ Aslaksen: Mathematics in Art and Architecture. Math.nus.edu.sg. Retrieved on 2013-04-16.
- ↑ Derry, Gregory N. (2002). What Science Is and How It Works. Princeton University Press. pp. 269-. ISBN 978-1-4008-2311-6.
- ↑ Dunlap, David W. (31 de julio de 2009). «Behind the Scenes: Edgar Martins Speaks». New York Times. Consultado el 11 de noviembre de 2014. «“My starting point for this construction was a simple statement which I once read (and which does not necessarily reflect my personal views): ‘Only a bad architect relies on symmetry; instead of symmetrical layout of blocks, masses and structures, Modernist architecture relies on wings and balance of masses.’».
- ↑ Marla Mallett Textiles & Tribal Oriental Rugs. The Metropolitan Museum of Art, New York.
- ↑ Dilucchio: Navajo Rugs. Navajocentral.org (2003-10-26). Retrieved on 2013-04-16.
- ↑ Quate: Exploring Geometry Through Quilts Archivado el 31 de diciembre de 2003 en Wayback Machine.. Its.guilford.k12.nc.us. Retrieved on 2013-04-16.
- ↑ Cucker, Felipe (2013). Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. Cambridge University Press. pp. 77–78, 83, 89, 103. ISBN 978-0-521-72876-8.
- ↑ «How to Design a Perfect Logo with Grid and Symmetry».
- ↑ Grammer, K.; Thornhill, R. (1994). «Human (Homo sapiens) facial attractiveness and sexual selection: the role of symmetry and averageness». Journal of Comparative Psychology (Washington, D.C.) 108 (3): 233-42. PMID 7924253. doi:10.1037/0735-7036.108.3.233.
- ↑ Rhodes, Gillian; Zebrowitz, Leslie, A. (2002). Facial Attractiveness - Evolutionary, Cognitive, and Social Perspectives. Ablex. ISBN 1-56750-636-4.
- ↑ Jones, B. C., Little, A. C., Tiddeman, B. P., Burt, D. M., & Perrett, D. I. (2001). Facial symmetry and judgements of apparent health Support for a “‘ good genes ’” explanation of the attractiveness – symmetry relationship, 22, 417–429.
- ↑ Arnheim, Rudolf (1969). Visual Thinking. University of California Press. (requiere registro).
- ↑ Jenny Lea Bowman (2009). «Symmetrical Aesthetics of Beowulf». University of Tennessee, Knoxville.
- ↑ Wald, 1984, p. 441-444.
- ↑ Lowe, John P; Peterson, Kirk (2005). Quantum Chemistry (Third edición). Academic Press. ISBN 0-12-457551-X.
- ↑ Mach, Ernst (1897). Symmetries and Group Theory in Particle Physics: An Introduction to Space-Time and Internal Symmetries. Open Court Publishing House.
- ↑ Wagemans, J. (1997). «Characteristics and models of human symmetry detection». Trends in Cognitive Sciences 1 (9): 346-352. PMID 21223945. S2CID 2143353. doi:10.1016/S1364-6613(97)01105-4.
- ↑ Bertamini, M. (2010). «Sensitivity to reflection and translation is modulated by objectness». Perception 39 (1): 27-40. PMID 20301844. S2CID 22451173. doi:10.1068/p6393.
- ↑ Barlow, H.B.; Reeves, B.C. (1979). «The versatility and absolute efficiency of detecting mirror symmetry in random dot displays». Vision Research 19 (7): 783-793. PMID 483597. S2CID 41530752. doi:10.1016/0042-6989(79)90154-8.
- ↑ Sasaki, Y.; Vanduffel, W.; Knutsen, T.; Tyler, C.W.; Tootell, R. (2005). «Symmetry activates extrastriate visual cortex in human and nonhuman primates». Proceedings of the National Academy of Sciences of the USA 102 (8): 3159-3163. PMC 549500. PMID 15710884. doi:10.1073/pnas.0500319102.
- ↑ Makin, A.D.J.; Rampone, G.; Pecchinenda, A.; Bertamini, M. (2013). «Electrophysiological responses to visuospatial regularity». Psychophysiology 50: 1045-1055. PMID 23941638. doi:10.1111/psyp.12082.
- ↑ Bertamini, M.; Silvanto, J.; Norcia, A.M.; Makin, A.D.J.; Wagemans, J. (2018). «The neural basis of visual symmetry and its role in middle and high-level visual processing». Annals of the New York Academy of Sciences 132: 280-293. PMID 29604083. doi:10.1111/nyas.13667.
- ↑ a b Perle, George (1992). «Symmetry, the twelve-tone scale, and tonality». Contemporary Music Review 6 (2): 81-96. doi:10.1080/07494469200640151.
- ↑ a b Perle, George (1990). The Listening Composer. University of California Press. p. 21. ISBN 978-0-520-06991-6.
Bibliografía[editar]
- Wald, Robert M.: General relativity, Chicago University Press, 1984, ISBN 0-226-87032-4.
- Sánchez Bautista F., Sánchez Hernández S. Laura: Texto y prácticas de diseño, 2011, ISBN 970-95086-0-1
Enlaces externos[editar]
 Wikcionario tiene definiciones y otra información sobre simetría.
Wikcionario tiene definiciones y otra información sobre simetría.
http://recursosbiblio.url.edu.gt/tesisjcem/2016/03/05/Letona-Diana-Investigacion.pdf
https://www.um.es/analesps/v17/v17_2/12-17_2.pdf
- Esta obra contiene una traducción parcial derivada de «Symmetry» de Wikipedia en inglés, concretamente de esta versión del 28 de mayo de 2021, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.








