Ley de la inversa del cuadrado
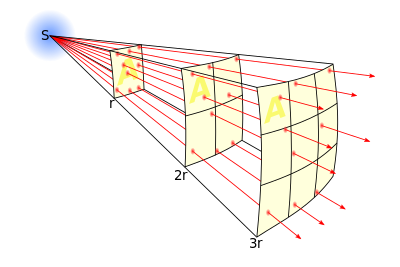
La ley de la inversa del cuadrado, ley cuadrática inversa o ley del cuadrado inverso de la distancia, se refiere a algunos fenómenos físicos cuya intensidad es inversamente proporcional al cuadrado de la distancia al centro donde se originan. En particular, se refiere a fenómenos ondulatorios (sonido y luz), y en general a campos centrales en un espacio euclídeo tridimensional, a campos eléctricos y a radiación ionizante no particulada.
Discusión
[editar]En mecánica ondulatoria la ley de la inversa del cuadrado establece que para una onda como, por ejemplo, el sonido o la luz, que se propaga desde una fuente puntual en todas direcciones por igual, la intensidad de la misma disminuye de acuerdo con el cuadrado de la distancia a la fuente de emisión. Esta ley se aplica naturalmente a la intensidad sonora y a la intensidad de luz (iluminación) y a los rayos X y radiación gamma, puesto que tanto el sonido como la luz son fenómenos ondulatorios (ondas electromagnéticas en el caso de la luz).
A distancias suficientemente grandes de los emisores de luz, radiación electro magnética o sonido, estos pueden ser vistos como fuentes puntuales. Por ejemplo, si se considera una fuente de luz pequeña y se hacen mediciones de la intensidad lumínica a una distancia d y a una distancia 2d, en el primer caso la intensidad es [(1/d)/(1/2d)]² = 4 veces mayor que en el segundo.
En teoría clásica de campos, en particular en campos centrales, la intensidad de campo también está gobernada por una ley de la inversa del cuadrado. Típicamente se observa en:
- La ley de la gravitación universal de Isaac Newton.
- El campo electrostático creado por una carga puntual.
El hecho de que los campos centrales disminuyan de intensidad según la inversa del cuadrado, está relacionado con que el espacio tiene tres dimensiones espaciales. De hecho, puede probarse que todo campo central que responde a la ecuación de Poisson en un espacio de D dimensiones decrece a grandes distancias como 1/rD-1, siendo r la distancia al centro de la fuente del campo.
Deducción de la ley inversa para ondas
[editar]La ley de la inversa del cuadrado para la intensidad de una onda sonora lumínica o de otro tipo puede ser deducida rigurosamente a partir de la ecuación de onda () y la definición de intensidad (), tal como sigue. Se parte de las siguientes ecuaciones:
(1)
(2)
Para una onda esférica emitida por una fuente puntual, Ψ sólo depende de la distancia r al centro de emisión y por tanto escribiendo el operador laplaciano que aparece en la ecuación de onda () en coordenadas esféricas para Ψ = Ψ(r,t) se tiene:
(1')
La solución de la ecuación de onda anterior, con c = ω/k, es:
Se puede aplicar la ecuación () para la intensidad o promedio cuadrático temporal <Ψ2>t es igual a:
Es decir, este último resultado muestra que la intensidad decrece con el cuadrado de la distancia al centro emisor, que es lo que se pretendía probar.
Deducción de la ley inversa para campos centrales
[editar]Si V(r) es un campo central y, por tanto, con simetría esférica, generado por una densidad de carga ρ o de masa concentrada y que satisface la ecuación de Laplace (), entonces el campo para distancias grandes de la fuente viene dado por la ecuación:
(3)
Que escribiendo en coordenadas esféricas el operador laplaciano para un espacio de D dimensiones nos lleva a:
(3')
La solución de esa ecuación se puede calcular muy fácilmente y es precisamente:
(4)
Donde kc es la constante del campo, p el valor total de la magnitud de la fuente (masa o carga total de la fuente que crea el campo) y D el número de dimensiones del espacio. Para un espacio tridimensional D = 3, el campo de fuerzas descrito por () viene dado por:
(5)
Es decir, un campo con simetría esférica descrito por el potencial () en un espacio de tres dimensiones debe decrecer según la ley inversa del cuadrado.
Espacios no euclídeos
[editar]La teoría de la relatividad afirma que en presencia de materia la geometría efectiva del espacio-tiempo no es euclídea, sino que existe una curvatura del espacio-tiempo. En esos casos el decaimiento según la ley de la inversa del cuadrado no es exacta y debe ajustarse de acuerdo a la curvatura. Por ejemplo, alrededor de una estrella con simetría esférica aun cuando el campo es radial, dado que la geometría viene dada por la métrica de Schwarzschild, la fuerza efectiva resulta ser como la de un campo gravitatorio clásico de la forma:
donde:
- es el momento angular el cuerpo respecto a la estrella.
- es la masa del cuerpo.
- es la velocidad de la luz.
Respecto a la forma global del universo, para un universo con tres dimensiones espaciales de curvatura positiva aproximadamente constante, la intensidad de un campo que emana de una fuente puede calcularse a partir del operador de Laplace-Beltrami
Obviamente, para distancias pequeñas comparadas con el inverso de la raíz cuadrada de la curvatura, la diferencia con un decaimiento según la inversa del cuadrado es inapreciable, pero a grandes distancias el efecto de la curvatura sí llega a hacerse notorio.















