Rotacional
En el cálculo vectorial, el rotacional o rotor es un operador vectorial sobre campos vectoriales definidos en un abierto de que muestra la tendencia de un campo vectorial a inducir rotación alrededor de un punto.
Matemáticamente, esta idea se expresa como el límite de la circulación del campo vectorial, cuando la curva sobre la que se integra se reduce a un punto:
Aquí, es el área de la superficie apoyada en la curva , que se reduce a un punto. El resultado de este límite no es el rotacional completo (que es un vector), sino solo su componente según la dirección normal a y orientada según la regla de la mano derecha. Para obtener el rotacional completo deberán calcularse tres límites, considerando tres curvas situadas en planos perpendiculares.
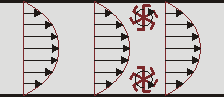
Aunque el que el rotacional de un campo alrededor de un punto sea distinto de cero no implica que las líneas de campo giren alrededor de ese punto y lo encierren. Por ejemplo, el campo de velocidades de un fluido que circula por una tubería (conocido como perfil de Poiseuille) posee un rotacional no nulo en todas partes, salvo en el eje central, pese a que la corriente fluye en línea recta:
La idea es que si colocamos una rueda de paletas infinitamente pequeña en el interior del campo vectorial, esta rueda girará, aunque el campo tenga siempre la misma dirección, debido a la diferente magnitud del campo a un lado y a otro de la rueda.
Historia[editar]
El concepto fue por primera vez usado por el matemático irlandés James MacCullagh en 1839[1][2] si bien no recibió su nombre y terminología modernas hasta el trabajo de compilación de teoría de campos de James Clerk Maxwell en 1871.[3]
Fuente vectorial y escalar[editar]
Al campo vectorial, , que se obtiene calculando el rotacional de un campo en cada punto,
se conoce como las fuentes vectoriales de (siendo las fuentes escalares las que se obtienen mediante la divergencia).
Un campo cuyo rotacional es nulo en todos los puntos del espacio se denomina irrotacional o se dice que carece de fuentes vectoriales. Y si está definido sobre un dominio simplemente conexo entonces dicho campo puede expresarse como el gradiente de una función escalar, o dicho de otra forma, el campo deriva de un potencial (es decir, es conservativo):
Expresión en coordenadas cartesianas[editar]
Partiendo de la definición mediante un límite, puede demostrarse que la expresión, en coordenadas cartesianas, del rotacional es
que se puede expresar de forma más concisa con ayuda del operador nabla como un producto vectorial, calculable mediante un determinante:
Debe tenerse muy presente que dicho determinante en realidad no es tal pues los elementos de la segunda fila no tienen argumento y por tanto carecen de sentido. Además, dicho determinante solo puede desarrollarse por la primera fila. En definitiva, la notación en forma de determinante sirve para recordar fácilmente la expresión del rotacional.
En la notación de Einstein, con el símbolo de Levi-Civita se escribe como:
Expresión en otros sistemas de coordenadas[editar]
Si se emplean sistemas de coordenadas diferentes del cartesiano, la expresión debe generalizarse, para incluir el que los vectores de la base dependen de la posición. Para un sistema de coordenadas ortogonales, como las cartesianas, las cilíndricas o las esféricas, la expresión general precisa de los factores de escala:
(donde, en cartesianas, y reobtenemos la expresión anterior. En coordenadas cilíndricas y en coordenadas esféricas ).
Expresión mediante formas diferenciales[editar]
Usando la derivada exterior, el rotacional se escribe simplemente como:
Obsérvese que tomando la derivada exterior de un campo (co)vectorial no da lugar a otro campo vectorial, sino a una 2-forma o un campo de bivector, escrito correctamente como . Sin embargo, puesto que los bivectores generalmente se consideran menos intuitivos que los vectores ordinarios, el R³-dual se utiliza comúnmente en lugar de otro: esto es una operación quiral, produciendo un pseudovector que adquiere valores opuestos en conjuntos coordenados izquierdos y derechos.
Propiedades[editar]
- Todo campo potencial (expresable como el gradiente de un potencial escalar) cuyo dominio es simplemente conexo es irrotacional y viceversa, esto es,
- Todo campo central (radial y dependiente solo de la distancia al centro) es irrotacional.
- En particular, el campo eléctrostático de una carga puntual (y por superposición, cualquier campo electrostático) es irrotacional.
- El rotacional de un campo vectorial es siempre un campo solenoidal, esto es, su divergencia siempre es nula:
Identidades[editar]
En general, en las coordenadas curvilíneas, (no solo en coordenadas cartesianas), el rotacional de un producto de vectores de campo v y F puede expresarse:
Intercambiando el vector de campo v y el operador ∇, llegamos al producto vectorial de un vector de campo con el rotacional de otro:
usando la notación de Feynman, ∇F, que opera solo con el vector de campo F.
Otra identidad es el rotacional del rotacional de un vector de campo. Puede ser expresado de la siguiente forma, en coordenadas cartesianas:
en esta identidad el Operador laplaciano de F se representa como ∇2F.
El rotacional del gradiente de cualquier campo escalar φ es siempre nulo
Si φ es una función escalar y F es un vector de campo, entonces:
Ejemplos[editar]
Un campo vectorial sencillo[editar]
Sea el campo vectorial:
que depende linealmente de x y y, que se muestra a continuación:

Mediante inspección visual, se observa que el campo está girando. Si indicáramos la dirección de un fluido y pusiéramos verticalmente una rueda de palas, de las que se utilizaban en los barcos de vapor, tendería a rotar en el sentido de las agujas del reloj. Utilizando la Regla de la mano derecha el vector rotacional apuntará a la parte negativa del eje zeta (hacia dentro) y no contendrá componentes en el eje x o y.
Calculando el rotacional:
Que está en la parte negativa del eje z, como se esperaba. En este caso, el rotacional es constante, independientemente de su posición. La "cantidad" de rotación es la misma en todo punto del espacio. La siguiente figura muestra el rotacional del campo vectorial en tres dimensiones.

Un ejemplo más complejo[editar]
Supongamos otro campo vectorial un poco más complejo:
Su gráfica es:

No se observa con facilidad que este campo sea rotacional, pero investigando un poco se puede observar que, por ejemplo, el campo es mayor en x=4 que en x=3. Al igual que en el caso anterior, si pusiéramos de nuevo una rueda de palas en la zona derecha del gráfico, la «corriente» más fuerte a la derecha haría rotar a la rueda en el sentido de las agujas del reloj, lo cual corresponde a un rotacional en la dirección negativa del eje z. Por contra, en la parte izquierda del gráfico se observa que la corriente más fuerte esta hacia la izquierda por lo que las palas girarían en el sentido contrario a las agujas del reloj y el rotacional, en este caso, apuntaría hacia la parte positiva el eje z. Calculando el rotacional podemos comprobar las suposiciones realizadas.
Efectivamente, el rotacional apunta a la dirección positiva del eje z para x negativa y a la parte negativa del eje z para x positivo. Obsérvese que el rotacional ya no es uniforme en todos los puntos:
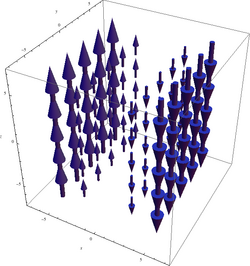
Obsérvese que el rotacional solamente depende de la coordenada x.
Otros ejemplos[editar]
- En un tornado los vientos están rotando sobre el ojo, y un campo vectorial que muestra las velocidades del viento tendría un rotacional diferente de cero en el ojo, y posiblemente en otras partes (véase vorticidad).
- En un campo vectorial que describa las velocidades lineales de cada parte individual de un disco que rota, el rotacional tendrá un valor constante en todas las partes del disco.
- Si una autopista fuera descrita con un campo vectorial, y los carriles tuvieran diversos límites de velocidad, el rotacional en las fronteras entre los carriles sería diferente de cero.
- La ley de Faraday de la inducción y la ley de Ampère-Maxwell, dos de las ecuaciones de Maxwell, se pueden expresar muy simplemente usando el rotacional. La primera indica que el rotacional de un campo eléctrico es igual a la tasa de variación de la densidad del flujo magnético, con signo opuesto debido a la Ley de Lenz; la segunda indica que el rotacional de un campo magnético es igual a la suma de la densidad de corrientes y la derivada temporal de la densidad de flujo eléctrico.
Véase también[editar]
Referencias[editar]
Bibliografía[editar]
- Spiegel, M. & Abellanas, L.: Fórmulas y tablas de matemática aplicada, Ed. McGraw-Hill, 1988. ISBN 84-7615-197-7.






















![{\displaystyle \nabla \times \left(\mathbf {v\times F} \right)=\left[\left(\mathbf {\nabla \cdot F} \right)+\mathbf {F\cdot \nabla } \right]\mathbf {v} -\left[\left(\mathbf {\nabla \cdot v} \right)+\mathbf {v\cdot \nabla } \right]\mathbf {F} \ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce40e8152b636cf496fdd637517b812b55dcf739)





![{\displaystyle {\nabla }\times \mathbf {F} =0{\boldsymbol {\hat {x}}}+0{\boldsymbol {\hat {y}}}+\left[{\frac {\partial }{\partial x}}(-x)-{\frac {\partial }{\partial y}}y\right]{\boldsymbol {\hat {z}}}=-2{\boldsymbol {\hat {z}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28cd3fa48f892c1df357ac7060797eb7dd1a8572)

