Ecuaciones de Maxwell
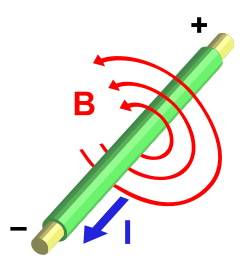

Las ecuaciones de Maxwell son un conjunto de cuatro ecuaciones (originalmente 20 ecuaciones) que describen por completo los fenómenos electromagnéticos. La gran contribución de James Clerk Maxwell fue reunir en estas ecuaciones largos años de resultados experimentales, debidos a Charles-Augustin de Coulomb, Carl Friederich Gauss, André-Marie Ampère, Michael Faraday entre otros, introduciendo los conceptos de campo y corriente de desplazamiento, unificando los campos eléctricos y magnéticos en un solo concepto: el campo electromagnético.[1]
Desarrollo histórico de las ecuaciones de Maxwell[editar]

Desde finales del siglo XVIII diversos científicos formularon leyes cuantitativas que relacionaban las interacciones entre los campos eléctricos, los campos magnéticos y las corrientes sobre conductores. Entre estas leyes están la ley de Ampère, la ley de Faraday o la ley de Lenz. Maxwell lograría unificar todas estas leyes en una descripción coherente del campo electromagnético.
Maxwell se dio cuenta de que la conservación de la carga eléctrica parecía requerir introducir un término adicional en la ley de Ampère. De hecho, actualmente se considera que uno de los aspectos más importantes del trabajo de Maxwell en el electromagnetismo es el término que introdujo en dicha ley: la derivada temporal de un campo eléctrico, conocida como corriente de desplazamiento. El trabajo que Maxwell publicó en 1865, A Dynamical Theory of the Electromagnetic Field, modificaba la versión de la ley de Ampère con lo que se predecía como la existencia de ondas electromagnéticas propagándose, dependiendo del medio material, a la velocidad de la luz en dicho medio. De esta forma Maxwell identificó la luz como una onda electromagnética, unificando así la óptica con el electromagnetismo.[2]
Exceptuando la modificación a la ley de Ampère, ninguna de las otras ecuaciones era original. Lo que hizo Maxwell fue reobtener dichas ecuaciones a partir de modelos mecánicos e hidrodinámicos usando su modelo de vórtices de líneas de fuerza de Faraday.
En 1884, Oliver Heaviside junto con Willard Gibbs agrupó estas ecuaciones y las reformuló en la notación vectorial actual. Sin embargo, es importante conocer que al hacer eso, Heaviside usó derivadas parciales temporales, diferentes a las derivadas totales usadas por Maxwell, en la ecuación (54). Ello provocó que se perdiera el término que aparecía en la ecuación posterior del trabajo de Maxwell (número 77). En la actualidad, este término se usa como complementario a estas ecuaciones y se conoce como fuerza de Lorentz.
La historia es aún confusa, debido a que el término ecuaciones de Maxwell se usa también para un conjunto de ocho ecuaciones en la publicación de Maxwell de 1865, A Dynamical Theory of the Electromagnetic Field, y esta confusión se debe a que seis de las ocho ecuaciones son escritas como tres ecuaciones para cada eje de coordenadas, así se puede uno confundir al encontrar veinte ecuaciones con veinte incógnitas. Los dos tipos de ecuaciones son casi equivalentes, a pesar del término eliminado por Heaviside en las actuales cuatro ecuaciones.
Detalle de las ecuaciones[editar]
Ley de Gauss para el campo eléctrico[editar]
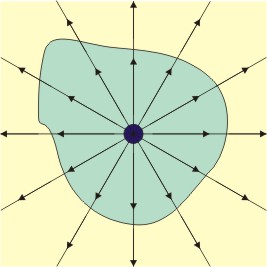
La ley de Gauss explica la relación entre el flujo del campo eléctrico a través una superficie cerrada con la carga neta encerrada por dicha superficie. Se define como flujo eléctrico () a la cantidad de fluido eléctrico que atraviesa una superficie dada. Análogo al flujo de la mecánica de fluidos, este fluido eléctrico no transporta materia, pero ayuda a analizar la cantidad de campo eléctrico () que pasa por una superficie S.[3] Matemáticamente se expresa como:
La ley dice que el flujo del campo eléctrico a través de una superficie cerrada es igual al cociente entre la carga (q) o la suma de las cargas que hay en el interior de la superficie y la permitividad eléctrica en el vacío (), así:[4][5]
La forma diferencial de la ley de Gauss, en forma local, afirma que por el teorema de Gauss-Ostrogradsky, la divergencia del campo eléctrico es proporcional a la densidad de carga eléctrica, es decir,
donde es la densidad de carga en el medio interior a la superficie cerrada. Intuitivamente significa que el campo E diverge o sale desde una carga , lo que se representa gráficamente como vectores que salen de la fuente que las genera en todas direcciones. Por convención si el valor de la expresión es positivo entonces los vectores salen, si es negativo estos entran a la carga.
Para casos generales se debe introducir una cantidad llamada densidad de flujo eléctrico () y nuestra expresión obtiene la forma:
Ley de Gauss para el campo magnético[editar]

Experimentalmente se llegó al resultado de que los campos magnéticos, a diferencia de los eléctricos, no comienzan y terminan en cargas diferentes. Esta ley primordialmente indica que las líneas de los campos magnéticos deben ser cerradas. En otras palabras, se dice que sobre una superficie cerrada, sea cual sea esta, no seremos capaces de encerrar una fuente o sumidero de campo, esto expresa la inexistencia del monopolo magnético. Al encerrar un dipolo en una superficie cerrada, no sale ni entra flujo magnético, por lo tanto el campo magnético no diverge, no sale de la superficie. Entonces la divergencia es cero.[6] Matemáticamente esto se expresa así:[5]
donde es la densidad de flujo magnético, también llamada inducción magnética. Es claro que la divergencia sea cero porque no salen ni entran vectores de campo sino que este hace caminos cerrados. El campo no diverge, es decir la divergencia de B es nula.
Su forma integral equivalente:
Como en la forma integral del campo eléctrico, esta ecuación solo funciona si la integral está definida en una superficie cerrada.
Ley de Faraday-Lenz[editar]
La ley de Faraday nos habla sobre la inducción electromagnética, la que origina una fuerza electromotriz en un campo magnético. Es habitual llamarla ley de Faraday-Lenz en honor a Heinrich Lenz ya que el signo menos proviene de la ley de Lenz. También se le llama como ley de Faraday-Henry, debido a que Joseph Henry descubrió esta inducción de manera separada a Faraday pero casi simultáneamente.[7] Lo primero que se debe introducir es la fuerza electromotriz (), si tenemos un campo magnético variable con el tiempo, una fuerza electromotriz es inducida en cualquier circuito eléctrico; y esta fuerza es igual a menos la derivada temporal del flujo magnético, así:[8]
- ,
como el campo magnético es dependiente de la posición tenemos que el flujo magnético es igual a:
- .
Además, el que exista fuerza electromotriz indica que existe un campo eléctrico que se representa como:
con lo que finalmente se obtiene la expresión de la ley de Faraday:[5]
Lo que indica que un campo magnético que depende del tiempo implica la existencia de un campo eléctrico, del que su circulación por un camino arbitrario cerrado es igual a menos la derivada temporal del flujo magnético en cualquier superficie limitada por el camino cerrado.
El signo negativo explica que el sentido de la corriente inducida es tal que su flujo se opone a la causa que lo produce, compensando así la variación de flujo magnético (ley de Lenz).
La forma diferencial local de esta ecuación es:
Es decir, el rotacional del campo eléctrico es la derivada parcial de la inducción magnética con respecto al tiempo.
Se interpreta como sigue: si existe una variación de campo magnético B entonces este provoca un campo eléctrico E o bien la existencia de un campo magnético no estacionario en el espacio libre provoca circulaciones del vector E a lo largo de líneas cerradas. En presencia de cargas libres, como los electrones, el campo E puede desplazar las cargas y producir una corriente eléctrica. Esta ecuación relaciona los campos eléctrico y magnético, y tiene otras aplicaciones prácticas como los motores eléctricos y los generadores eléctricos y explica su funcionamiento. Más precisamente, demuestra que un voltaje puede ser generado variando el flujo magnético que atraviesa una superficie dada.
Ley de Ampère generalizada[editar]
André-Marie Ampère formuló una relación para un campo magnético inmóvil y una corriente eléctrica que no varía en el tiempo. La ley de Ampère dice que la circulación en un campo magnético () a lo largo de una curva cerrada C es igual a la densidad de corriente () sobre la superficie encerrada en la curva C, matemáticamente así:[5]
donde es la permeabilidad magnética en el vacío.
Pero cuando esta relación se la considera con campos que sí varían a lo largo del tiempo llega a cálculos erróneos, como el de violar la conservación de la carga.[9] Maxwell corrigió esta ecuación para lograr adaptarla a campos no estacionarios y posteriormente pudo ser comprobada experimentalmente por Heinrich Rudolf Hertz.
Maxwell reformuló esta ley así:[5]
- .
En el caso específico estacionario esta relación corresponde a la ley de Ampère, además confirma que un campo eléctrico que varía con el tiempo produce un campo magnético y además es consecuente con el principio de conservación de la carga.[9]
En forma diferencial, esta ecuación toma la forma:
- .
En forma sencilla esta ecuación explica que si se tiene un conductor, un alambre recto por el que circula una densidad de corriente J, esta provoca la aparición de un campo magnético B rotacional alrededor del alambre y que el rotor de B apunta en el mismo sentido que J.
En medios materiales[editar]
Para el caso de que las cargas estén en medios materiales, y asumiendo que estos son lineales, homogéneos, isótropos y no dispersivos, se puede encontrar una relación entre los vectores intensidad eléctrica e inducción magnética mediante dos parámetros conocidos como permitividad eléctrica y la permeabilidad magnética:[10]
Pero estos valores también dependen del medio material, por lo que se dice que un medio es lineal cuando la relación entre E/D y B/H es lineal. Si esta relación es lineal, matemáticamente se puede decir que y están representadas por una matriz 3x3. Si un medio es isótropo es porque esta matriz ha podido ser diagonalizada y consecuentemente es equivalente a una función ; si en esta diagonal uno de los elementos es diferente del otro se dice que es un medio anisótropo. Estos elementos también son llamados constantes dieléctricas y, cuando estas constantes no dependen de su posición, el medio es homogéneo.[11]
Los valores de y en medios lineales no dependen de las intensidades del campo. Por otro lado, la permitividad y la permeabilidad son escalares cuando las cargas están en medios homogéneos e isótropos. Los medios heterogéneos e isótropos dependen de las coordenadas de cada punto por lo que los valores, escalares, van a depender de la posición. Los medios anisótropos son tensores.[10] Finalmente, en el vacío tanto como son cero porque suponemos que no hay fuentes.
En la siguiente tabla encontramos las ecuaciones como se las formula en el vacío y en la materia.[12]
| En el vacío | En la materia |
|---|---|
Ecuaciones de Maxwell[editar]
Las ecuaciones de Maxwell como ahora las conocemos son las cuatro citadas anteriormente y a manera de resumen se pueden encontrar en la siguiente tabla:
| Nombre | Forma diferencial | Forma integral |
|---|---|---|
| Ley de Gauss: | ||
| Ley de Gauss para el campo magnético: | ||
| Ley de Faraday: | ||
| Ley de Ampère generalizada: |
Estas cuatro ecuaciones junto con la fuerza de Lorentz son las que explican cualquier tipo de fenómeno electromagnético. La importancia de las ecuaciones de Maxwell es que permanecen invariantes con cualquier sistema de unidades, salvo con pequeñas excepciones, y que son compatibles con la relatividad especial y general. Además Maxwell descubrió que la cantidad era simplemente la velocidad de la luz en el vacío, por lo que la luz es una forma de radiación electromagnética. Los valores aceptados actualmente para la velocidad de la luz, la permitividad y la permeabilidad magnética se resumen en la siguiente tabla:
| Símbolo | Nombre | Valor numérico | Unidad de medida SI | Tipo |
|---|---|---|---|---|
| Velocidad de la luz en el vacío | metros por segundo | definido | ||
| Permitividad del vacío | faradios por metro | derivado | ||
| Permeabilidad magnética | henrios por metro | definido hasta 2019
ahora es un valor derivado |
Potencial escalar y potencial vector[editar]
Como consecuencia matemática de las ecuaciones de Maxwell y además con el objetivo de simplificar sus cálculos se han introducido los conceptos de potencial vector () y potencial escalar (). Este potencial vector no es único y no tiene significado físico claro pero se sabe que un elemento infinitesimal de corriente da lugar a una contribución paralela a la corriente.[13] Este potencial se obtiene como consecuencia de la ley de Gauss para el flujo magnético, ya que se conoce que si la divergencia de un vector es cero, ese vector como consecuencia define a un rotacional, así:[14]
A partir de este potencial vector y de la ley de Faraday puede definirse un potencial escalar así:[12]
donde el signo menos () es por convención. Estos potenciales son importantes porque poseen una simetría gauge que nos da cierta libertad a la hora de escogerlos.[12] El campo eléctrico en función de los potenciales:
Hallamos que con la introducción de estas cantidades las ecuaciones de Maxwell quedan reducidas solo a dos, puesto que, la ley de Gauss para el campo magnético y la ley de Faraday quedan satisfechas por definición. Así la ley de Gauss para el campo eléctrico escrita en términos de los potenciales:
y la ley de ampère generalizada
.
Nótese que se ha pasado de un conjunto de cuatro ecuaciones diferenciales parciales de primer orden a solo dos ecuaciones diferenciales parciales pero de segundo orden. Sin embargo, estas ecuaciones se pueden simplificar con ayuda de una adecuada elección del gauge.
Consecuencias físicas de las ecuaciones[editar]
Principio de conservación de la carga[editar]
Las ecuaciones de Maxwell llevan implícitas el principio de conservación de la carga. El principio afirma que la carga eléctrica no se crea ni se destruye, ni global ni localmente, sino que únicamente se transfiere; y que si en una superficie cerrada está disminuyendo la carga contenida en su interior, debe haber un flujo de corriente neto hacia el exterior del sistema. Es decir la densidad de carga y la densidad de corriente satisfacen una ecuación de continuidad.
A partir de la forma diferencial de la ley de Ampère se tiene:
que al reemplazar la ley de Gauss y tomar en cuenta que (para cualquier vector ), se obtiene:
o bien en forma integral: .
Ecuaciones originales de Maxwell[editar]
En el capítulo III de A Dynamical Theory of the Electromagnetic Field, titulado «Ecuaciones generales del campo electromagnético», Maxwell formuló ocho ecuaciones que nombró de la A a la H.[15] Estas ecuaciones llegaron a ser conocidas como «las ecuaciones de Maxwell», pero ahora este epíteto lo reciben las ecuaciones que agrupó Heaviside. La versión de Heaviside de las ecuaciones de Maxwell realmente contiene solo una ecuación de las ocho originales, la ley de Gauss que en el conjunto de ocho sería la ecuación G. Además Heaviside fusionó la ecuación A de Maxwell de la corriente total con la ley circuital de Ampère que en el trabajo de Maxwell era la ecuación C. Esta fusión, que Maxwell por sí mismo publicó en su trabajo On Physical Lines of Force de 1861 modifica la ley circuital de Ampère para incluir la corriente de desplazamiento de Maxwell.
Las ocho ecuaciones originales de Maxwell pueden ser escritas en forma vectorial así:
| Denominación | Nombre | Ecuación |
|---|---|---|
| A | Corriente de desplazamiento | |
| B | Ecuación de Fuerza magnética | |
| C | Ley circuital de Ampère | |
| D | Fuerza de Lorentz | |
| E | Ecuación de electricidad elástica | |
| F | Ley de Ohm | |
| G | Ley de Gauss | |
| H | Ecuación de continuidad de carga |
donde: es el vector intensidad de campo magnético (llamado por Maxwell como intensidad magnética); es la densidad de corriente eléctrica y es la corriente total incluida la corriente de desplazamiento; es el campo desplazamiento (desplazamiento eléctrico); es la densidad de carga libre (cantidad libre de electricidad); es el vector potencial magnético (impulso magnético); es el campo eléctrico (fuerza electromotriz [no confundir con la actual definición de fuerza electromotriz]); es el potencial eléctrico y es la conductividad eléctrica (resistencia específica, ahora solo resistencia).
Maxwell no consideró a los medios materiales en general, esta formulación inicial usa la permitividad y la permeabilidad en medios lineales, isótropos y no dispersos, a pesar de que también se las puede usar en medios anisótropos.
Maxwell incluyó el término en la expresión de la fuerza electromotriz de la ecuación D, que corresponde a la fuerza magnética por unidad de carga en un conductor que se mueve a una velocidad . Esto significa que la ecuación D es otra formulación de la fuerza de Lorentz. Esta ecuación primero apareció como la ecuación 77 de la publicación On Physical Lines of Force de Maxwell, anterior a la publicación de Lorentz. En la actualidad esta fuerza de Lorentz no forma parte de las ecuaciones de Maxwell pero se la considera una ecuación adicional fundamental en el electromagnetismo.
Expresión de las ecuaciones en relatividad[editar]
En la relatividad especial, las ecuaciones de Maxwell en el vacío se escriben mediante unas relaciones geométricas, las cuales toman la misma forma en cualquier sistema de referencia inercial. Estas ecuaciones están escritas en términos de cuadrivectores y tensores contravariantes, que son objetos geométricos definidos en M4. Estos objetos se relacionan mediante formas diferenciales en relaciones geométricas que al expresarlas en componentes de los sistemas coordenados Lorentz proporcionan las ecuaciones para el campo electromagnético.
La cuadricorriente está descrita por una 1-forma y lleva la información sobre la distribución de cargas y corrientes. Sus componentes son:
Que debe cumplir la siguiente relación geométrica para que se cumpla la ecuación de continuidad.
Escrito en componentes de los sistemas coordenados Lorentz queda:
Para poner en correspondencia objetos del mismo rango, se utiliza el operador de Laplace-Beltrami o laplaciana definida como:
Podemos poner en correspondencia el cuadrivector densidad de corriente con otro objeto del mismo rango como es el cuadripotencial, que lleva la información del potencial eléctrico y el potencial vector magnético.
O escrito en coordenadas Lorentz obtenemos que:
Expresión que reproduce las ecuaciones de onda para los potenciales electromagnéticos.
La 1-forma A lleva la información sobre los potenciales de los observadores inerciales siendo sus componentes:
Para obtener el objeto geométrico que contiene los campos, tenemos que subir el rango de A mediante el operador diferencial exterior obteniendo la 2-forma F campo electromagnético. En forma geométrica podemos escribir:
Que expresado para un sistema inercial Lorentz tenemos que:
Con lo que obtenemos el tensor de campo electromagnético.
Primer par de ecuaciones de Maxwell[editar]
Las siguientes expresiones ligan los campos con las fuentes, relacionamos la cuadricorriente con el tensor campo electromagnético mediante la forma geométrica:
o bien en coordenadas Lorentz:
Obtención de las ecuaciones[editar]
Para un observable en S partiendo de expresión en coordenadas Lorentz podemos obtener:
- Para tenemos que: , entonces:
Por tanto:
- Para podemos obtener de la misma forma que:
Segundo par de ecuaciones de Maxwell[editar]
Corresponden a las ecuaciones homogéneas. Escritas en forma geométrica tenemos que:
Que corresponden con la expresión en los sistemas coordenados Lorentz:
Donde el tensor es el tensor dual de F. Se obtiene mediante el operador de Hodge.
Obtención de las ecuaciones[editar]
- Para :
Por tanto:
- Para se obtiene la ecuación vectorial:
La propiedad reproduce las ecuaciones de Maxwell internas, que se puede expresar como , que se puede escribir en los sistemas coordenados Lorentz como:
Podemos resumir el conjunto de expresiones que relacionan los objetos que describen el campo electromagnético en la siguiente tabla. La primera columna son las relaciones geométricas, independientes de cualquier observador; la segunda columna son las ecuaciones descritas mediante un sistema coordenado Lorentz; y la tercera es la descripción de la relación y la ley que cumple.
| Forma geométrica | Covariante Lorentz | Descripción |
|---|---|---|
| Condición/gauge de Lorenz (*) | ||
| Definición de campos electromagnéticos | ||
| Ecuación de onda | ||
| Ecuaciones de Maxwell | ||
| Ley de conservación de la carga |
(*) Existe una confusión habitual en cuanto a la nomenclatura de este gauge. Las primeras ecuaciones en las que aparece tal condición (1867) se deben a Ludvig V. Lorenz, no al mucho más conocido Hendrik A. Lorentz. (Véase: J.D. Jackson: Classical Electrodynamics, 3rd edition p.294)
Finalmente el cuadrigradiente se define así:
Los índices repetidos se suman de acuerdo al convenio de sumación de Einstein. De acuerdo con el cálculo tensorial, los índices pueden subirse o bajarse por medio de la matriz fundamental g.
El primer tensor es una expresión de dos ecuaciones de Maxwell, la ley de Gauss y la ley de Ampère generalizada; la segunda ecuación es consecuentemente una expresión de las otras dos leyes.
Se ha sugerido que el componente de la fuerza de Lorentz se puede derivar de la ley de Coulomb y por eso la relatividad especial asume la invarianza de la carga eléctrica.[16][17]
Expresión de las ecuaciones para una frecuencia constante[editar]
En las ecuaciones de Maxwell, los campos vectoriales no son solo funciones de la posición, en general son funciones de la posición y del tiempo, como por ejemplo . Para la resolución de estas ecuaciones en derivadas parciales, las variables posicionales se encuentran con la variable temporal. En la práctica, la resolución de dichas ecuaciones pueden contener una solución armónica (sinusoidal).
Con ayuda de la notación compleja se puede evitar la dependencia temporal de los resultados armónicos, eliminando así el factor complejo de la expresión . Gran parte de las resoluciones de las ecuaciones de Maxwell toman amplitudes complejas, además de no ser solo función de la posición. En lugar de la derivación parcial en el tiempo se tiene la multiplicación del factor imaginario , donde es la frecuencia angular.
En la forma compleja, las ecuaciones de Maxwell toman la siguiente forma:[10]
Véase también[editar]
- Electromagnetismo
- James Clerk Maxwell, Oliver Heaviside
- Carga
- Onda electromagnética, ecuación de onda electromagnética
- Ecuaciones de Jefimenko
- Ley de Gauss, Ley de Faraday, Ley de Ampère
- Divergencia, Rotacional
- Teoría del absorbedor de Wheeler-Feynman
- Ecuaciones de Maxwell explicadas para noobs
Referencias[editar]
- ↑ «Ecuaciones de Maxwell». 1999 de agosto. Archivado desde el original el 23 de enero de 2008. Consultado el 15 de enero de 2008.
- ↑ Ángel Franco García: Universidad del País Vasco (octubre de 2006). «El espectro electromagnético». Consultado el 15 de enero de 2008.
- ↑ «Teorema de Gauss y Flujo Eléctrico». Archivado desde el original el 29 de enero de 2008. Consultado el 19 de enero de 2008.
- ↑ «Línea de cargas. Ley de Gauss». Consultado el 18 de enero de 2008.
- ↑ a b c d e Richard Feynman (1974). Feynman lectures on Physics Volume 2 (en inglés). Addison Wesley Longman. ISBN 0-201-02115-3.
- ↑ «Magnetostática». Consultado el 19 de enero de 2008.
- ↑ «Concepto de Flujo». Consultado el 19 de enero de 2008.
- ↑ «Ley de Faraday-Henry». Consultado el 19 de enero de 2008.
- ↑ a b «Ley de Ampere-Maxwell». Consultado el 20 de enero de 2008.
- ↑ a b c Ángel Cardama Aznar (2002). Antenas. UPC. ISBN 84-8301-625-7.
- ↑ Liliana I. Pérez. «APUNTE:Ecuaciones de Maxwell». Archivado desde el original el 23 de noviembre de 2018. Consultado el 22 de enero de 2008.
- ↑ a b c La web de Física (2008). «Ecuaciones de Maxwell». Consultado el 23 de enero de 2008.
- ↑ «Potencial Vector Magnético». Archivado desde el original el 1 de septiembre de 2007. Consultado el 21 de enero de 2008.
- ↑ «Ecuaciones del Electromagnetismo». Consultado el 21 de enero de 2008.
- ↑ «Professor Clerk Maxwell on the electromagnetic field» (en inglés). Consultado el 21 de enero de 2008.
- ↑ L. D. Landau, E. M. Lifshitz (1980). The Classical Theory of Fields (en inglés). Butterworth-Heinemann. ISBN 0-7506-2768-9.
- ↑ Richard E Haskell (2006). «Special relativity and Maxwell equations» (en inglés). Archivado desde el original el 1 de enero de 2008. Consultado el 23 de enero de 2008.
Enlaces externos[editar]
- On Physical Lines of Force
 Wikisource en inglés contiene obras originales de o sobre Ecuaciones de Maxwell.
Wikisource en inglés contiene obras originales de o sobre Ecuaciones de Maxwell.- Monografías.com archivo sobre ecuaciones de Maxwell
- Modelo de Maxwell Archivado el 19 de enero de 2008 en Wayback Machine.
- A treatise on electricity and magnetism (1873) Vol. 1 PDF
- A treatise on electricity and magnetism (1873) Vol. 2 PDF



























































































![{\displaystyle \mu _{0}c\rho (\mathbf {r} ,t)=\partial _{1}F^{10}+\partial _{2}F^{20}+\partial _{3}F^{30}={\frac {1}{c}}\left[{\frac {\partial E_{x}}{\partial x}}+{\frac {\partial E_{y}}{\partial y}}+{\frac {\partial E_{z}}{\partial z}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0748536a35274344bc726ffdf04f4294bd1d9eb5)






![{\displaystyle \partial _{\mu }*F^{\mu 0}=\partial _{1}*F^{10}+\partial _{2}*F^{20}+\partial _{3}*F^{30}=\left[{\frac {\partial B_{x}}{\partial x}}+{\frac {\partial B_{y}}{\partial y}}+{\frac {\partial B_{z}}{\partial z}}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f9407e838017e819dc8ccd58764f4afac6545f9)


















