Ley de Gauss
En física, la ley de Gauss, relacionada con el teorema de la divergencia o teorema de Gauss,[1] establece que el flujo de ciertos campos a través de una superficie cerrada es proporcional a la magnitud de las fuentes de dicho campo que hay en el interior de la misma superficie. Estos campos son aquellos cuya intensidad decrece como la distancia a la fuente al cuadrado. La constante de proporcionalidad depende del sistema de unidades empleado.
Se aplica al campo electrostático y al gravitatorio. Sus fuentes son la carga eléctrica y la masa, respectivamente. También puede aplicarse al campo magnetostático.
La ley fue formulada por Carl Friedrich Gauss en 1835, pero no fue publicado hasta 1867.[2] Esta es una de las cuatro ecuaciones de Maxwell, que forman la base de electrodinámica clásica (las otras tres son la ley de Gauss para el magnetismo, la ley de Faraday de la inducción y la ley de Ampère con la corrección de Maxwell). La ley de Gauss puede ser utilizada para obtener la ley de Coulomb,[3] y viceversa.
Flujo del campo eléctrico[editar]

El flujo (denotado como ) es una propiedad de cualquier campo vectorial referida a una superficie hipotética que puede ser cerrada o abierta. Para un campo eléctrico, el flujo () se mide por el número de líneas de fuerza que atraviesan la superficie.
Para definir al flujo eléctrico con precisión considérese la figura, que muestra una superficie cerrada arbitraria ubicada dentro de un campo eléctrico.
La superficie se encuentra dividida en cuadrados elementales , cada uno de los cuales es lo suficientemente pequeño como para que pueda ser considerado como un plano. Estos elementos de área pueden ser representados como vectores , cuya magnitud es la propia área, la dirección es perpendicular a la superficie y hacia afuera.
En cada cuadrado elemental también es posible trazar un vector de campo eléctrico . Ya que los cuadrados son tan pequeños como se quiera, puede considerarse constante en todos los puntos de un cuadrado dado.
y caracterizan a cada cuadrado y forman un ángulo entre sí y la figura muestra una vista amplificada de dos cuadrados.
El flujo, entonces, se define como sigue:
(1)
O sea:
(2)
Flujo para una superficie cilíndrica en presencia de un campo uniforme[editar]

Supóngase una superficie cilíndrica colocada dentro de un campo uniforme tal como muestra la figura:
El flujo puede escribirse como la suma de tres términos, (a) una integral en la tapa izquierda del cilindro, (b) una integral en la superficie cilíndrica y (c) una integral en la tapa derecha:
(3)
Para la tapa izquierda, el ángulo , para todos los puntos, es de , tiene un valor constante y los vectores son todos paralelos.
Entonces:
(4)
siendo el área de la tapa. Análogamente, para la tapa derecha:
(5)
Finalmente, para la superficie cilíndrica:
(6)
Por consiguiente: da cero ya que las mismas líneas de fuerza que entran, después salen del cilindro.
(7)
Flujo para una superficie esférica con una carga puntual en su interior[editar]

Considérese una superficie esférica de radio r con una carga puntual q en su centro tal como muestra la figura. El campo eléctrico es paralelo al vector superficie , y el campo es constante en todos los puntos de la superficie esférica.
En consecuencia:
(8)
Deducciones[editar]
Deducción de la ley de Gauss a partir de la ley de Coulomb[editar]
Este teorema aplicado al campo eléctrico creado por una carga puntual es equivalente a la ley de Coulomb de la interacción electrostática.
La ley de Gauss puede deducirse matemáticamente a través del uso del concepto de ángulo sólido, que es un concepto muy similar a los factores de vista conocidos en la transferencia de calor por radiación.
El ángulo sólido que es subtendido por sobre una superficie esférica, se define como:
siendo el radio de la esfera.
como el área total de la esfera es el ángulo sólido para ‘’toda la esfera’’ es:
la unidad de este ángulo es el estereorradián (sr)
Si el área no es perpendicular a las líneas que salen del origen que subtiende a , se busca la proyección normal, que es:
Si se tiene una carga "q" rodeada por una superficie cualquiera, para calcular el flujo que atraviesa esta superficie es necesario encontrar para cada elemento de área de la superficie, para luego sumarlos. Como la superficie que puede estar rodeando a la carga puede ser tan compleja como quiera, es mejor encontrar una relación sencilla para esta operación:
De esta manera es el mismo ángulo sólido subentendido por una superficie esférica. como se mostró un poco más arriba para cualquier esfera, de cualquier radio. de esta forma al sumar todos los flujos que atraviesan a la superficie queda:
que es la forma integral de la ley de Gauss. La ley de Coulomb también puede deducirse a través de Ley de Gauss.
Forma diferencial e integral de la ley de Gauss[editar]
Forma diferencial de la ley de Gauss[editar]
Tomando la ley de Gauss en forma integral.
Aplicando al primer término el teorema de Gauss de la divergencia queda
Como ambos lados de la igualdad poseen diferenciales volumétricas, y esta expresión debe ser cierta para cualquier volumen, solo puede ser que:
Que es la forma diferencial de la ley de Gauss (en el vacío).
Esta ley se puede generalizar cuando hay un dieléctrico presente, introduciendo el campo de desplazamiento eléctrico , de esta manera la ley de Gauss se puede escribir en su forma más general como
Finalmente es de esta forma en que la ley de Gauss es realmente útil para resolver problemas complejos de maneras relativamente sencillas.
Forma integral de la ley de Gauss[editar]
Su forma integral utilizada en el caso de una distribución extensa de carga puede escribirse de la manera siguiente:
donde es el flujo eléctrico, es el campo eléctrico, es un elemento diferencial del área A sobre la cual se realiza la integral, es la carga total encerrada dentro del área A, es la densidad de carga en un punto de y es la permitividad eléctrica del vacío.
Interpretación[editar]


La ley de Gauss puede ser utilizada para demostrar que no existe campo eléctrico dentro de una jaula de Faraday. La ley de Gauss es la equivalente electrostática a la ley de Ampère, que es una ley de magnetismo. Ambas ecuaciones fueron posteriormente integradas en las ecuaciones de Maxwell.
Esta ley puede interpretarse, en electrostática, entendiendo el flujo como una medida del número de líneas de campo que atraviesan la superficie en cuestión. Para una carga puntual este número es constante si la carga está contenida por la superficie y es nulo si está fuera (ya que hay el mismo número de líneas que entran como que salen). Además, al ser la densidad de líneas proporcional a la magnitud de la carga, resulta que este flujo es proporcional a la carga, si está encerrada, o nulo, si no lo está.
Cuando tenemos una distribución de cargas, por el principio de superposición, sólo tendremos que considerar las cargas interiores, resultando la ley de Gauss.
Sin embargo, aunque esta ley se deduce de la ley de Coulomb, es más general que ella, ya que se trata de una ley universal, válida en situaciones no electrostáticas en las que la ley de Coulomb no es aplicable.
Aplicaciones[editar]
Distribución lineal de carga[editar]
Sea una recta cargada a lo largo del eje z. Tomemos como superficie cerrada un cilindro de radio r y altura h con su eje coincidente al eje z. Expresando el campo en coordenadas cilíndricas tenemos que debido a la simetría de reflexión respecto a un plano z=cte el campo no tiene componente en el eje z y la integración a las bases del cilindro no contribuye, de modo que aplicando la ley de Gauss:
Debido a la simetría del problema el campo tendrá dirección radial y podemos sustituir el producto escalar por el producto de módulos (ya que la dirección de la superficie lateral también es radial).
Despejando el campo y añadiendo su condición radial obtenemos:
Distribución esférica de carga[editar]
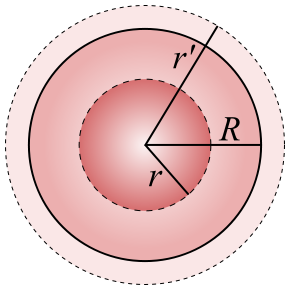
Considérese una esfera uniformemente cargada de radio R. La carga existente en el interior de una superficie esférica de radio r es una parte de la carga total, que se calcula multiplicando la densidad de carga por el volumen de la esfera de radio r:
Si Q es la carga de la esfera de radio R, entonces, se tiene:
Dividiendo miembro a miembro ambas expresiones y operando apropiadamente:
Como se demostró en una sección anterior y teniendo en cuenta que según la ley de Gauss , se obtiene:
Por lo tanto, para puntos interiores de la esfera:
Y para puntos exteriores:
En el caso de que la carga se distribuyera en la superficie de la esfera, es decir, en el caso de que fuera conductora, para puntos exteriores a la misma la intensidad del campo estaría dada por la segunda expresión, pero para puntos interiores a la esfera, el valor del campo sería nulo ya que la superficie gaussiana que se considerara no encerraría carga alguna.
Ley de Gauss para el campo magnetostático[editar]

Al igual que para el campo eléctrico, existe una ley de Gauss para el magnetismo, que se expresa en sus formas integral y diferencial como
Esta ley expresa la inexistencia de cargas magnéticas o, como se conocen habitualmente, monopolos magnéticos. Las distribuciones de fuentes magnéticas son siempre neutras en el sentido de que posee un polo norte y un polo sur, por lo que su flujo a través de cualquier superficie cerrada es nulo.
En el hipotético caso de que se descubriera experimentalmente la existencia de monopolos, esta ley debería ser modificada para acomodar las correspondientes densidades de carga, resultando una ley en todo análoga a la ley de Gauss para el campo eléctrico. La ley de Gauss para el campo magnético quedaría como
donde densidad de corriente , la cual obliga a modificar la ley de Faraday
Caso gravitacional[editar]
Dada la similitud entre la ley de Newton de la gravitación universal y la ley de Coulomb, puede deducirse una ley análoga para el campo gravitatorio, la cual se escribe
|
|
|
|
siendo G la constante de gravitación universal, y G vectorial el campo gravitatorio. El signo menos en esta ley y el hecho de que la masa siempre sea positiva significa que el campo gravitatorio siempre es atractivo y se dirige hacia las masas que lo crean.
Sin embargo, a diferencia de la ley de Gauss para el campo eléctrico, el caso gravitatorio es sólo aproximado y se aplica exclusivamente a masas pequeñas en reposo, para las cuales es válida la ley de Newton. Al modificarse la teoría de Newton mediante la Teoría de la Relatividad general, la ley de Gauss deja de ser cierta, ya que deben incluirse la gravitación causada por la energía y el efecto del campo gravitatorio en el propio espaciotiempo (lo que modifica la expresión de los operadores diferenciales e integrales).
- Es posible comparar ambas ya que podemos medir el flujo de propiedades que disminuyan con el cuadrado de la distancia , y esto lo tienen en común la fórmula del campo eléctrico con la del campo gravitatorio : Campo Eléctrico y Campo Gravitatorio .
Ley de Gauss para los dieléctricos[editar]

Un dieléctrico, en presencia de un campo eléctrico, sufre lo que se llama polarización. La polarización consiste en la separación de las cargas positivas y negativas del dieléctrico, ya que el campo eléctrico acelera las cargas positivas en la dirección del campo y las negativas en la dirección opuesta. Las cargas generadas por este efecto de polarización se denominan cargas ligadas. El material pasa a estar constituido por dipolos, como se muestra en la figura. De este modo, las cargas están "unidas" a los dipolos, no son libres de moverse. A su vez, el resto de las cargas, que no fueron generadas por este efecto de polarización, se denominan cargas libres. Las cargas libres son las cargas a las que se está más acostumbrado cuando se estudia la electrostática.[4]
Véase también[editar]
- Campo eléctrico
- Campo vectorial
- Carl Friedrich Gauss
- Densidad de flujo eléctrico
- Dieléctrico
- Ecuaciones de Maxwell
- Electromagnetismo
- Flujo
- Gravedad
- Ley de Coulomb
- Método de las imágenes
- Superficie de Gauss
- Superficie (topología)
- Teorema de la divergencia
- Teoría de distribuciones
Referencias[editar]
- ↑ The Feynman Lectures on Physics, Vol II.
- ↑ Bellone, Enrico (1980). A World on Paper: Studies on the Second Scientific Revolution.
- ↑ Halliday, David; Resnick, Robert (1970). Fundamentals of Physics. John Wiley & Sons, Inc. pp. 452-53.
- ↑ Griffiths, D. J. Introduction to Electrodynamics, 3a ed. New Jersey: Prentice Hall (1999) (en inglés).
Bibliografía adicional[editar]
- Jackson, John David (1999). Electrodinámica clásica, 3.º ed., Nueva York: Wiley.































































