Fuerza magnética

De Wikipedia, la enciclopedia libre

La fuerza magnética es la parte de la fuerza electromagnética total o fuerza de Lorentz que mide un observador sobre una distribución de cargas en movimiento. Las fuerzas magnéticas son producidas por el movimiento de partículas cargadas, como por ejemplo electrones, lo que indica la estrecha relación entre la electricidad y el magnetismo.

[editar] Fuerza magnética sobre un conductor

Un conductor es un hilo o alambre por el que circula una corriente eléctrica. Una corriente eléctrica es un conjunto de cargas eléctricas en movimiento. Ya que un campo magnético ejerce una fuerza lateral sobre una carga en movimiento, es de esperar que la resultante de las fuerza sobre cada carga resulte en una fuerza lateral sobre un alambre que lleva corriente.

[editar] Conductor rectilíneo

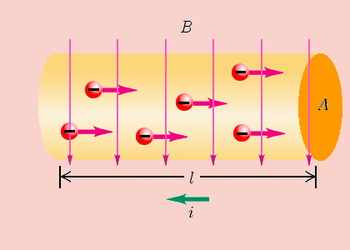
La figura muestra un tramo de alambre de longitud $\,\!l$ que lleva una corriente $\,\!i$ y que está colocado en una campo magnético $\,\! \vec B$ Para simplificar se ha orientado el vector densidad de corriente $\,\!j$ de tal manera que sea perpendicular a $\,\! \vec B$ .

La corriente $\,\!i$ en un conductor rectilíneo es transportada por electrones libres, siendo $\,\!n$ el número de estos electrones por unidad de volumen del alambre. La magnitud de la fuerza media que obra en uno de estos electrones está dada por;

$F^ \prime=q_0vB \sin \theta = ev_dB$

por ser $\,\! \theta = 90 ^ \circ$ y siendo $\,\! v_d$ la velocidad de arrastre: $v_d = \frac {j}{ne}$ . Por lo tanto,

$F^ \prime = e \left ( \frac{j}{ne} \right )B = \frac{jB}{n}$

La longitud $\,\!l$ del conductor contiene $\,\!nAl$ electrones libres, siendo $\,\!Al$ el volumen de la sección de conductor de sección transversal $\,\!A$ que se está considerando. La fuerza total sobre los electrones libres en el conductor y, por consiguiente, en el conductor mismo, es:

$F = e \left ( nAl \right )F^ \prime = nAl\frac{jB}{n}$

Ya que $\,\!jA$ es la corriente $\,\!i$ en el conductor, se tiene:

$\,\!F=ilB$

Las cargas negativas que se mueven hacia la derecha en el conductor equivalen a cargas positivas moviéndose hacia la izquierda, esto es, en la dirección de la flecha verde. Para una de estas cargas positivas, la velocidad $\,\!v$ apuntaría hacia la izquierda y la fuerza sobre el conductor $\,\!F = q_0v \times B$ apunta hacia arriba saliendo del plano de la figura. Esta misma conclusión se deduce si se consideran los portadores de carga negativos reales para los cuales $\,\!v$ apunta hacia la derecha, pero $\,\!q_0$ tiene signo negativo. Así pues, midiendo la fuerza magnética lateral que obra sobre un conductor con corriente y colocado en un campo magnético, no es posible saber si los portadores de corriente son cargas negativas moviéndose en una dirección o cargas positivas que se mueven en dirección opuesta.

La ecuación anterior es válida solamente si el conductor es perpendicular a $\,\!B$ . Es posible expresar el caso más general en forma vectorial así:

$\,\! \vec F=i \vec l \times \vec B$

siendo $\,\!l$ un vector (recorrido) que apunta a lo largo del conductor en el sentido de la corriente. Esta ecuación es equivalente a la relación $\,\! \vec F=q_0 \vec v \times \vec B$ y cualquiera de las dos puede tomarse como ecuación de definición de $\,\!B$

Obsérvese que $\vec l$ (no representado en la figura) apunta hacia la izquierda y que la fuerza magnética $(\vec F = i \vec l \times \vec B)$ apunta hacia arriba saliendo del plano de la figura.

Esto concuerda con la conclusión a que se llegó al analizar las fuerzas que obran en los portadores de carga individuales

[editar] Conductor no rectilíneo

Si se considera solamente un elemento diferencial de un conductor de longitud $d \vec l$ , la fuerza $d \vec F$ puede encontrarse mediante la expresión

$d \vec F = i d \vec l \times \vec B$

Integrando esta fórmula de la manera apropiada es posible encontrar la fuerza $\vec F$ sobre un conductor no lineal.

Considérese, por ejemplo, un alambre de la forma mostrada en la figura, que lleva una corriente i y se encuentra en el seno de un campo magnético uniforme de inducción magnética $\,\! B$ saliendo del plano de la figura tal como lo muestran los puntos. La magnitud de la fuerza sobre cada tramo recto está dada por:

$\,\! F_1 = F_3 = i l B$

y apunta hacia abajo tal como lo muestran los vectores coloreados de verde. Un segmento de alambre de longitud $\,\!d \vec l$ en el arco experimenta una fuerza $d \vec F$ cuya magnitud es:

$\,\! dF = iBdl = iB(Rd\theta)$

y cuya direccón es radial hacia O, que es el centro del arco. Solamente la componente hacia abajo de esa fuerza es efectiva, porque la componente horizontal es anulada por una componente directamente opuesta proveniente del correspondiente segmento de arco a la derecha de O. En consecuencia, la fuerza total sobre el semicírculo de alamabre alrededor de O apunta hacia abajo y es: