Fuerza conservativa

En física, un campo de fuerzas es conservativo si el trabajo total realizado por el campo sobre una partícula que realiza un desplazamiento en una trayectoria cerrada (como la órbita de un planeta) es nulo. El nombre conservativo se debe a que para una fuerza de ese tipo existe una forma especialmente simple (en términos de energía potencial) de la ley de conservación de la energía. Las fuerzas que dependen solo de la posición son típicamente conservativas. Un ejemplo de fuerza conservativa es la fuerza gravitatoria de la mecánica newtoniana. Las fuerzas dependientes del tiempo o de la velocidad (por ejemplo, la fricción o rozamiento) son típicamente no conservativas. La mayoría de los sistemas físicos fuera del equilibrio termodinámico son no-conservativos; en ellos la energía se disipa por procesos análogos al rozamiento.
Criterios de caracterización de una fuerza conservativa[editar]
Puede demostrarse que un campo es conservativo si presenta alguna de las propiedades siguientes (de hecho, si cumple una de ellas, cumplirá las otras ya que matemáticamente son equivalentes en un conjunto abierto simplemente conexo):
- Hay un campo escalar con:
(1)
- donde es el gradiente del campo escalar V(r).
- El trabajo
(2a)
- a lo largo de un camino cualquiera L a través del campo de fuerza depende solo de los puntos inicial y final y no de la trayectoria. En particular, el trabajo por una curva cerrada C es cero, también
(2b)
- El campo es simplemente continuo y cumple la condición de integrabilidad:
(3). Eso significa que, si la rotación desaparece, también lo hará
Conservatividad local[editar]
Cuando se considera el criterio () se debe tener precaución, porque el campo de fuerza puede existir, pero la rotación la hace no conservativa. El ejemplo más conocido es el conductor eléctrico, a cuyo campo magnético asociado se lo representa como:
Aunque la condición integral se cumple, no existe la derivada en el punto cero, por lo que la región no es continua. Entonces no se trata de un campo gradiente, como puede distinguir de la integral cerrada de un círculo unitario. El círculo unitario se parametriza mediante
con .
Con eso la integral cerrada es:
Es un campo no conservativo, ya que integral a lo largo de una curva cerrada como lo es una circunferencia de radio 1 centrada en el origen es diferente de cero.
Potencial[editar]
El campo escalar del criterio () se llama potencial o energía potencial. El signo menos de este criterio es una convención y tiene un significado profundo, a pesar de que su significado fue argumentado en el principio variacional de la mecánica lagrangiana y, por el momento, opera de forma voluntaria. La base de esa convención se puede aclarar por medio del siguiente ejemplo: en la cercanía de la superficie terrestre está la masa m en un potencial gravitacional a una altura h=y bajo una aceleración de la gravedad g > 0, aproximadamente v(y)= + m g y. Debido al sistema de coordenadas en la superficie terrestre es positivo cuando se dirige hacia arriba, debe ser negativo cuando se dirige hacia abajo. Se calcula la fuerza del primer criterio y se obtiene:
Esto muestra que la fuerza se ejerce, tal como se esperaba, en dirección al centro de la Tierra.
Demostración de equivalencia de los criterios[editar]
Existen tres criterios equivalentes para determinar si un campo de fuerzas es conservativo ((), () y ()). El primer criterio es acerca de la definición de un campo de fuerzas conservativo; los otros dos son otras formulaciones del primer criterio. Muchas veces el campo de fuerzas está definido de una forma "directa" a través del segundo criterio. Así, se tiene que el trabajo en un campo conservativo es independiente del camino.
Se tiene un camino cerrado C en un campo conservativo, del punto 1 sobre el camino S1 al punto 2 luego por el camino S2 de regreso al punto 1.
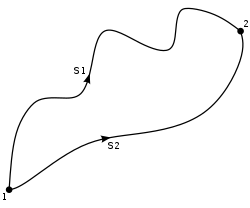
.
La integral cerrada sobre ese camino será:
Para todos los caminos S1, S2 esta integral sería S1 + (-S2) igual a cero, cuando:
También sería:
esto es la independencia del camino recorrido y con esto se describe las posibles definiciones de un campo conservativo.
El tercer criterio habla sobre la desaparición de la rotación de un campo de fuerzas conservativas. Por el primer criterio se tiene y para la rotación se tiene que
con lo que el primer y el tercer criterio resultan ser equivalentes. Esto también es equivalente al segundo criterio. Si , por medio del teorema de Stokes para la curva cerrada C, se tiene para una superficie cerrada A:
Con lo que el trabajo vuelve a aparecer y éste desde la primera demostración se obtuvo que era independiente del camino, por lo que se tiene finalmente una igualación de los tres criterios.
Conservación de la energía[editar]
En la mecánica clásica se tiene que la energía cinética es: , donde v es la velocidad; de la segunda ley de Newton, para masas m constantes, la energía puede ser descrita como: Tenemos la integral para el camino del punto 1 al punto 2
- .
Para el lado derecho de la ecuación
Lo que significa que el trabajo total que se necesita para el movimiento corresponde al cambio en la energía cinética. Para el lado izquierdo se obtiene mediante el uso de las propiedades de la fuerza conservativa
y con esto
respectivamente
que se refiere directamente a la conservación de la energía. Las propiedades de la conservación de la energía son también la base, de ahí que el campo conservativo lleva su nombre, aquí la energía se conserva. Pero no solo el concepto de conservación va ligado a la energía, también va ligado al de la masa, que en campos relativistas están muy enlazados.
Ejemplos[editar]
Fuerzas conservativas[editar]
En física clásica:
Campos conservativos[editar]
El campo electrostático, el campo gravitatorio en mecánica clásica o las fuerzas intermoleculares en un sólido para pequeños valores de vibración son todos ellos casos de fuerzas conservativas. El campo electrostático y el gravitatorio en mecánica clásica de un cuerpo en reposo y a grandes distancias del mismo tiene la forma aproximada:
Donde es un vector unitario dirigido desde la fuente del campo hacia el punto donde se mide el campo, son respectivamente el vector de posición del punto donde se mide el campo, el vector posición de la carga que crea el campo electrostático y el vector de la posición de la masa que crea el campo gravitatorio
Las fuerzas intermoleculares pueden ser escritas por unas fuerzas del tipo:
Donde representa el vector de posición de la molécula i-ésima y las son constantes elásticas que dependen de la red cristalina del material o su estructura interna.
La energía potencial es el correspondiente problema de oscilaciones acopladas y viene dado por una forma cuadrática de las coordenadas:
Fuerzas no conservativas[editar]
Las fuerzas no conservativas son aquellas en las que el trabajo realizado por las mismas es distinto de cero a lo largo de un camino cerrado. El trabajo realizado por las fuerzas no conservativas es dependiente del camino tomado. A mayor recorrido, mayor trabajo realizado.
Ejemplos de fuerzas no conservativas serían:
Campos no conservativos[editar]
El campo magnético es un ejemplo de campo no conservativo que no puede ser derivado de un potencial escalar. Esto se refleja por ejemplo que las líneas del campo magnético son cerradas.
Propiedades[editar]
Dado un campo vectorial definido sobre una región simplemente conexa el campo es conservativo si cumple cualquiera de estas condiciones (de hecho, puede demostrarse que si cumple una de ellas cumple las otras dos también):
- 1. Un campo es conservativo si, y solo si, el trabajo que realiza la fuerza que genera el campo entre dos puntos no depende del camino que haya seguido el móvil entre esos dos puntos.
- 2. Un campo es conservativo si, y solo si, el rotacional de ese campo vectorial en todos los puntos es cero:.
- 3. Y más importante: un campo de fuerzas es conservativo si y solo si podemos encontrar una función escalar potencial llamada de energía potencial, de la cual su gradiente sea esa fuerza. De tal modo que para esa fuerza el trabajo que realiza sobre un móvil entre dos puntos cualesquiera del espacio es igual a la variación de esa función escalar entre esos dos puntos, cambiada de signo.
Otra propiedad interesante es que las curvas integrales de un campo vectorial conservativo, llamadas líneas de campo, no pueden ser cerradas.






















![{\displaystyle E=\int _{t_{1}}^{t_{2}}\mathbf {F} [\mathbf {r} (t),\mathbf {v} (t),t]\,\mathbf {v} (t)\,\mathrm {d} t=\int _{t_{1}}^{t_{2}}m\cdot {\frac {d\mathbf {v} (t)}{dt}}\,\mathbf {v} (t)\,\mathrm {d} t.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebfaf90c0937be68d17677ef5381557d138cf8a7)


![{\displaystyle \int _{1,S1}^{2}\mathbf {F} \,\mathrm {d} \mathbf {r} =-\int _{1,S1}^{2}\nabla V\,\mathrm {d} \mathbf {r} =-[V(r_{2})-V(r_{1})]=V_{1}-V_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1b5b9c4dcbdca6bcb49d97908f19874f55ed69b)












