Plano inclinado

El plano inclinado (también conocido como rampa o pendiente) es una máquina simple que consiste en una superficie plana que forma un ángulo agudo con el suelo y se utiliza para elevar cuerpos a cierta altura.[1] Tiene la ventaja de que se requiere una fuerza menor a la empleada para levantar dicho cuerpo verticalmente (gracias a la descomposición de fuerzas), aunque se deba aumentar la distancia recorrida y vencer la fuerza de rozamiento.
Visión general[editar]


Un plano inclinado es una superficie de apoyo plana inclinada en ángulo, con un extremo más alto que el otro, que se utiliza como ayuda para subir o bajar una carga.[2][3][4] El plano inclinado es una de las seis máquinas simples clásicas definidas por los científicos del Renacimiento. Se utilizan mucho para mover cargas pesadas sobre obstáculos verticales; los ejemplos varían desde una rampa utilizada para cargar mercancías en un camión, hasta una persona que camina por una rampa para peatones, hasta un automóvil o un tren que sube una pendiente.[4]
Mover un objeto por un plano inclinado requiere menos fuerza que levantarlo hacia arriba, a costa de un aumento en la distancia recorrida.[5] Su ventaja mecánica, el factor por el que se reduce la fuerza, es igual a la relación entre la longitud de la superficie inclinada y la altura que salva. Debido al principio de conservación de la energía, se requiere la misma cantidad de energía mecánica (trabajo) para levantar un objeto dado una distancia vertical dada, sin tener en cuenta las pérdidas por fricción, pero el plano inclinado permite realizar el mismo trabajo con una fuerza menor ejercida sobre una distancia mayor.[6][7]
El ángulo de fricción,[8], también llamado a veces ángulo de reposo,[9] es el ángulo máximo en el que una carga puede permanecer inmóvil en un plano inclinado debido a la fricción, sin deslizarse hacia abajo. Este ángulo es igual al arcotengente del coeficiente de fricción μs entre las superficies.[9]
A menudo se considera que otras dos máquinas simples se derivan del plano inclinado.[10] La cuña se puede considerar un plano inclinado en movimiento o dos planos inclinados conectados en la base.[6] El tornillo consiste en un plano inclinado angosto envuelto alrededor de un cilindro.[6]
El término también puede referirse a una aplicación específica, como en el caso de una rampa recta excavada en una ladera empinada para permitir el transporte de mercancías hacia arriba y hacia abajo. Puede incluir vagones sobre raíles o tirados por un sistema de cables; un funicular o ferrocarril por cable, como el Plano Inclinado de Johnstown.
Las leyes que rigen el comportamiento de los cuerpos en un plano inclinado fueron enunciadas por primera vez por el matemático Simon Stevin, en la segunda mitad del siglo XVI.[11]
Para analizar las fuerzas existentes sobre un cuerpo situado sobre un plano inclinado, hay que tener en cuenta la existencia de varios orígenes en ellas.
- En primer lugar se debe considerar la existencia de una fuerza de gravedad, también conocida como peso, que es consecuencia de la masa (M) que posee el cuerpo apoyado en el plano inclinado y tiene una magnitud de M.g con una dirección vertical[12] y representada en la figura por la letra G.
- Existe además una fuerza normal (N), también conocida como la fuerza de reacción ejercida sobre el cuerpo por el plano como consecuencia de la tercera ley de Newton, se encuentra en una dirección perpendicular al plano[12] y tiene una magnitud igual a la fuerza ejercida por el plano sobre el cuerpo. En la figura aparece representada por N y tiene la misma magnitud que F2= M.g.cos α y sentido opuesto a la misma.
- Existe finalmente una fuerza de rozamiento, también conocida como fuerza de fricción (FR), que siempre se opone al sentido del movimiento del cuerpo respecto a la superficie,[13] y cuya magnitud depende tanto del peso como de las características superficiales del plano inclinado y la superficie en contacto del cuerpo que proporcionan un coeficiente de rozamiento. Esta fuerza debe tener un valor igual a F1=M.g.sen α, para que el cuerpo se mantenga en equilibrio. En el caso en que F1 fuese mayor que la fuerza de rozamiento el cuerpo se deslizaría hacia abajo por el plano inclinado. Por tanto para subir el cuerpo se debe realizar una fuerza con una magnitud que iguale o supere la suma de F1 + FR.
Historia[editar]
| Demostración de Stevin |
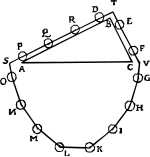
Como señaló Dijksterhuis, el argumento de Stevin[17] no es completamente estricto. Las fuerzas ejercidas por la parte colgante de la cadena no necesitan ser simétricas porque la parte colgante “no necesita conservar su forma” cuando se suelta. Incluso si la cadena se suelta con un momento angular cero, el movimiento, incluidas las oscilaciones, es posible a menos que la cadena esté inicialmente en su configuración de equilibrio, una suposición que haría que el argumento fuera circular. |
Se han utilizado planos inclinados desde tiempos prehistóricos para mover objetos pesados.[18][19] Los caminos inclinados y los pedraplenes construidos por civilizaciones antiguas como los romanos son ejemplos de los primeros planos inclinados que han sobrevivido y muestran que entendieron el valor de este dispositivo para mover cargas cuesta arriba. Se cree que las piedras pesadas utilizadas en estructuras de piedra antiguas como Stonehenge[20] se movieron y colocaron en su lugar usando planos inclinados hechos de tierra,[21] aunque es difícil encontrar evidencia de tales rampas de construcción temporales. Las pirámides de Egipto se construyeron utilizando planos inclinados, y rampas de asedio[22][23][24] permitieron a los ejércitos antiguos superar las murallas de las fortalezas. Los antiguos griegos construyeron una rampa pavimentada de 6 km (3,7 millas) de largo, el Diolkos, para arrastrar barcos por tierra a través del istmo de Corinto.[5]
Sin embargo, el plano inclinado fue la última de las seis máquinas simples clásicas en ser reconocida como tal. Esto probablemente se deba a que es un dispositivo pasivo e inmóvil (la carga es la parte móvil),[25] y también a que se encuentra en la naturaleza en forma de pendientes y colinas. Aunque entendieron su uso para levantar objetos pesados, los filósofos de la antigua Grecia que definieron las otras cinco máquinas simples, no incluyeron el plano inclinado.[26] Este punto de vista persistió entre algunos científicos posteriores; y en una fecha tan tardía como 1826 Karl von Langsdorf escribió que un plano inclinado "... no es más una máquina que la pendiente de una montaña".[25] El problema de calcular la fuerza requerida para empujar un peso hacia arriba en un plano inclinado (su ventaja mecánica) fue analizado por los filósofos griegos Herón de Alejandría (c. 10 - 60 EC) y Papo de Alejandría (c. 290 - 350 EC), pero ambos se equivocaron en su resolución.[27][28][29]
No fue hasta el Renacimiento cuando el plano inclinado se resolvió matemáticamente y se clasificó con las otras máquinas simples. El primer análisis correcto del plano inclinado apareció en la obra del enigmático autor del siglo XIII Jordanus Nemorarius,[30][31] aunque su solución del problema aparentemente no fue comunicada a otros filósofos de la época.[28] Gerolamo Cardano (1570) propuso la solución incorrecta de que la fuerza a aplicar es proporcional al ángulo del plano.[14] Posteriormente, a finales del siglo XVI, Michael Varro (1584), Simon Stevin (1586) y Galileo Galilei (1592) publicaron tres soluciones correctas a lo largo de diez años.[28] Aunque no fue la primera, la deducción del ingeniero flamenco Simon Stevin[29] es la más conocida, por su originalidad y el uso de un collar de cuentas (véase el recuadro).[16][30] En 1600, el científico italiano Galileo incluyó el plano inclinado en su análisis de máquinas simples en Le Meccaniche ("Sobre la mecánica"), mostrando su similitud subyacente con las otras máquinas como un amplificador de fuerza.[32]
Las primeras reglas elementales para deslizar objetos con fricción sobre un plano inclinado fueron descubiertas por Leonardo da Vinci (1452-1519), pero quedaron inéditas en sus cuadernos.[33] Fueron redescubiertas por Guillaume Amontons (1699) y Charles-Augustin de Coulomb (1785) las desarrolló aún más.[33] Leonhard Euler (1750) demostró que la tangente del ángulo de rozamiento interno en un plano inclinado es proporcional a la fricción.[34]
Aplicaciones[editar]
Los planos inclinados se utilizan mucho en forma de "rampas" para cargar y descargar mercancías en camiones, barcos y aviones.[4] Las rampas para sillas de ruedas se utilizan para permitir que las personas con movilidad reducida superen obstáculos verticales sin exceder su fuerza. Las escalera mecánicas y las cintas transportadoras inclinadas también son formas de plano inclinado.[7] En un funicular o ferrocarril por cable, un vagón de ferrocarril se sube por un plano inclinado con cables. Los planos inclinados también permiten que tanto personas como objetos pesados y frágiles salven de forma segura un desnivel vertical utilizando la fuerza normal del plano para distribuir el efecto de la gravedad. Las rampas de evacuación de las aeronaves permiten que las personas alcancen el suelo de forma rápida y segura desde la altura del compartimento de pasajeros de un avión comercial.
Otros planos inclinados se construyen en estructuras permanentes. Las carreteras para vehículos y los ferrocarriles tienen planos inclinados en forma de pendientes graduales, rampas y pedraplenes para permitir que los vehículos superen obstáculos verticales como colinas sin perder tracción en la superficie de la carretera.[4] De manera similar, los senderos para peatones y las aceras disponen de rampas suaves para limitar su pendiente, con el fin de garantizar que los peatones puedan mantener las condiciones de tracción necesarias.[2][5] Los planos inclinados también se utilizan como entretenimiento para que las personas se deslicen hacia abajo de forma controlada, en toboganes, rampas acuáticas, esquí alpino y pistas de patinaje.
Terminología[editar]
Pendiente[editar]
El efecto de utilizar un plano inclinado depende de su pendiente, es decir, de su gradiente o inclinación. Cuanto menor sea la pendiente, mayor será la ventaja mecánica y menor la fuerza necesaria para levantar un peso dado. La pendiente s de un plano es igual a la diferencia de altura entre sus dos extremos, o "desnivel", dividida por su longitud horizontal, o "carrera".[35] También se puede expresar por el ángulo que forma el plano con la horizontal, θ.

Ventaja mecánica[editar]
La ventaja mecánica VM de una máquina simple se define como la relación entre la fuerza resultante sobre la carga y la fuerza aplicada. Para el plano inclinado, la fuerza a vencer es solo la fuerza gravitatoria sobre el objeto cargado en el plano, su peso Fp. La fuerza aplicada es Fi ejercida sobre el objeto, paralelamente al plano, para moverlo hacia arriba remontando la rampa. Las ventajas mecánicas son...
La ventaja mecánica VM de un plano inclinado ideal sin fricción se denomina a veces "ventaja mecánica ideal" (VMI), mientras que cuando se incluye la fricción se denomina "ventaja mecánica real" (VMR).[36]
Plano inclinado sin fricción[editar]

Si no hay fricción entre el objeto que se mueve y el plano, el dispositivo se denomina "plano inclinado ideal". Se puede abordar esta condición si el objeto está rodando, como un barril, o apoyado sobre ruedas. Debido al principio de conservación de la energía, para un plano inclinado sin fricción, el trabajo realizado sobre la carga que se levanta, Wres, es igual a la fuerza aplicada por la distancia recorrida, Wap[37][38][39]
El trabajo se define como la fuerza multiplicada por el desplazamiento que mueve un objeto. El trabajo realizado sobre la carga es igual a su peso multiplicado por el desplazamiento vertical que sube, que es la "elevación" del plano inclinado.
El trabajo aplicado es igual a la fuerza Fap ejercida sobre el objeto multiplicada por la longitud de la diagonal del plano inclinado.
Sustituyendo estos valores en la ecuación de conservación de energía anterior y reorganizando los sumandos
Para expresar la ventaja mecánica en función del ángulo θ del plano,[38] se puede ver en el diagrama de arriba que
Entonces
En consecuencia, la ventaja mecánica de un plano inclinado sin fricción es igual al recíproco del seno del ángulo de inclinación. La fuerza aplicada Fap de esta ecuación es la fuerza necesaria para mantener la carga inmóvil en el plano inclinado o empujarla hacia arriba a una velocidad constante. Si la fuerza de entrada es mayor que el valor anterior, la carga acelerará hacia arriba en el plano; si la fuerza es menor, acelerará hacia abajo.
Plano inclinado con rozamiento[editar]
Donde hay fricción entre el plano y la carga, como por ejemplo con una caja pesada que se desliza por una rampa, parte del trabajo aplicado por la fuerza de entrada se disipa como calor por fricción, Wfric, por lo que se realiza menos trabajo en la carga. Debido a conservación de la energía, la suma del trabajo de salida y las pérdidas de energía por fricción es igual al trabajo de entrada
Por lo tanto, se requiere más fuerza de entrada y la ventaja mecánica es menor que si no hubiera fricción. Con la fricción, la carga solo se moverá si la fuerza neta paralela a la superficie es mayor que la fuerza de fricción Ff que se opone a ella.[9][40][41] La fuerza de fricción máxima viene dada por
donde Fn es la fuerza normal entre la carga y el plano, en dirección normal a la superficie, y μ es la fricción entre las dos superficies, que varía con el material. Cuando no se aplica ninguna fuerza de entrada, si el ángulo de inclinación θ del plano es menor que un valor máximo φ, la componente de la fuerza gravitatoria paralela al plano será demasiado pequeña para superar la fricción y la carga permanecerá inmóvil. Este ángulo se denomina ángulo de rozamiento interno y depende de la composición de las superficies, pero es independiente del peso de la carga. A continuación se muestra que la tangente del ángulo de reposo φ es igual a μ
Con fricción, siempre hay algún rango de fuerza aplicada Fap para el cual la carga es estacionaria, (es decir, ni se desliza hacia arriba ni hacia abajo), mientras que con un plano inclinado sin fricción solo hay un valor particular de fuerza de entrada para la cual la carga está estacionaria.
Análisis[editar]

Una carga que descansa sobre un plano inclinado, cuando se considera como un cuerpo libre tiene tres fuerzas actuando sobre ella:[9][40][41]
- La fuerza aplicada, Fap ejercida sobre la carga para moverla, que actúa paralela al plano inclinado.
- El peso de la carga, Fp, que actúa verticalmente hacia abajo
- La fuerza del plano sobre la carga, que se puede descomponer en dos componentes:
- La fuerza normal Fn del plano inclinado sobre la carga que la soporta. Esta se dirige perpendicular (normal) a la superficie.
- La fuerza de fricción, Ff del plano sobre la carga actúa paralela a la superficie, y siempre tiene una dirección opuesta al movimiento del objeto. Es igual a la fuerza normal multiplicada por el coeficiente de fricción μ entre las dos superficies.
Usando las leyes de Newton, la carga estará estacionaria o en movimiento constante si la suma de las fuerzas sobre ella es cero. Dado que la dirección de la fuerza de fricción es opuesta para el caso de movimiento cuesta arriba y cuesta abajo, estos dos casos deben considerarse por separado:
- Movimiento cuesta arriba: La fuerza total sobre la carga es hacia el lado cuesta arriba, por lo que la fuerza de fricción se dirige hacia abajo en el plano, oponiéndose a la fuerza aplicada.
|
Demostración de la ventaja mecánica para el movimiento cuesta arriba
Las ecuaciones de equilibrio para fuerzas paralelas y perpendiculares al plano son
|
- La ventaja mecánica es
- donde . Esta es la condición para el "movimiento inminente" hacia arriba del plano inclinado. Si la fuerza aplicada Fap es mayor que la dada por esta ecuación, la carga se moverá hacia arriba en el plano.
- Movimiento cuesta abajo: La fuerza total sobre la carga es hacia el lado cuesta abajo, por lo que la fuerza de fricción se dirige hacia arriba del plano.
|
Demostración de la ventaja mecánica para el movimiento cuesta abajo
Las ecuaciones de equilibrio son
|
- La ventaja mecánica es
- Esta es la condición para el movimiento inminente hacia abajo del plano; si la fuerza aplicada Fi es menor que la dada en esta ecuación, la carga se deslizará por el plano. Hay tres casos:
- : La ventaja mecánica es negativa. En ausencia de fuerza aplicada, la carga permanecerá inmóvil y requiere alguna fuerza aplicada negativa (cuesta abajo) para deslizarse hacia abajo.
- : El águlo de reposo. La ventaja mecánica es infinita. Sin fuerza aplicada, la carga no se deslizará, pero la más mínima fuerza negativa (cuesta abajo) hará que se deslice.
- : La ventaja mecánica es positiva. En ausencia de fuerza aplicada, la carga se deslizará hacia abajo del plano y requiere una fuerza positiva (cuesta arriba) para mantenerla inmóvil.
Ventaja mecánica utilizando potencia[editar]

La ventaja mecánica de un plano inclinado es la relación entre el peso de la carga sobre la rampa y la fuerza requerida para hacerla subir. Si la energía no se disipa ni se almacena en el movimiento de la carga, esta ventaja mecánica puede calcularse a partir de las dimensiones de la rampa.
Para demostrar esto, sea r la posición de un vagón en una rampa con un ángulo θ por encima de la horizontal, dada por
donde R es la distancia en la rampa. La velocidad del vagón en la rampa es ahora
Debido a que no hay pérdidas, la potencia utilizada por la fuerza "F" para subir la carga por la rampa es igual a la potencia resultante, que es la elevación vertical del peso "p" de la carga.
La potencia de entrada que hace subir el vagón por la rampa está dada por
y la potencia resultante es
Igualando la potencia aplicada y la potencia resultante, se obtiene la ventaja mecánica como
La ventaja mecánica de una rampa inclinada también se puede calcular a partir de la relación entre la longitud de la rampa L y su altura vertical V, porque el seno del ángulo de la rampa está dado por
por lo tanto,
Ejemplo: si la altura de una rampa es V = 1 metro y su longitud es L = 5 metros, entonces la ventaja mecánica es
lo que significa que una fuerza de 20 kg levantará una carga de 100 kg.
El plano inclinado Liverpool Minard tiene unas dimensiones de 1804 metros por 37,50 metros de desnivel, lo que proporciona una ventaja mecánica de
por lo que una fuerza de tensión de 100 kp en el cable levantará una carga de 4810 kp. El grado de esta pendiente es del 2 %, lo que significa que el ángulo θ es lo suficientemente pequeño como para que sen θ=tan θ.
Referencias[editar]
- ↑ Tipler, Paul Allen (1991). Física preuniversitaria. Reverte. ISBN 9788429143751. Consultado el 20 de febrero de 2018.
- ↑ a b Cole, Matthew (2005). Explore science, 2nd Ed.. Pearson Education. p. 178. ISBN 978-981-06-2002-8.
- ↑ Merriam-Webster's collegiate dictionary, 11th Ed.. Merriam-Webster. 2003. pp. 629. ISBN 978-0-87779-809-5. «inclined plane definition dictionary.»
- ↑ a b c d «The Inclined Plane». Math and science activity center. Edinformatics. 1999. Consultado el 11 de marzo de 2012.
- ↑ a b c Silverman, Buffy (2009). Simple Machines: Forces in Action, 4th Ed.. USA: Heinemann-Raintree Classroom. p. 7. ISBN 978-1-4329-2317-4.
- ↑ a b c Ortleb, Edward P.; Richard Cadice (1993). Machines and Work. Lorenz Educational Press. pp. iv. ISBN 978-1-55863-060-4.
- ↑ a b Reilly, Travis (24 de noviembre de 2011). «Lesson 04:Slide Right on By Using an Inclined Plane». Teach Engineering. College of Engineering, Univ. of Colorado at Boulder. Archivado desde el original el 8 de mayo de 2012. Consultado el 8 de septiembre de 2012.
- ↑ Scott, John S. (1993). Dictionary of Civil Engineering. Chapman & Hill. p. 14. ISBN 978-0-412-98421-1. «angle of friction [mech.] in the study of bodies sliding on plane surfaces, the angle between the perpendicular to the surface and the resultant force (between the body and the surface) when the body begins to slide. angle of repose [s.m.] for any given granular material the steepest angle to the horizontal at which a heaped surface will stand in stated conditions.»
- ↑ a b c d Ambekar, A. G. (2007). Mechanism and Machine Theory. PHI Learning. p. 446. ISBN 978-81-203-3134-1. «Angle of repose is the limiting angle of inclination of a plane when a body, placed on the inclined plane, just starts sliding down the plane.»
- ↑ Rosen, Joe; Lisa Quinn Gothard (2009). Encyclopedia of Physical Science, Volume 1. Infobase Publishing. p. 375. ISBN 978-0-8160-7011-4.
- ↑ Ignacio, Ramírez Vargas; Manuel, Palacios Pineda, Luis; E, Rodríguez C. , Mario. Estática para ingeniería. Grupo Editorial Patria. ISBN 9786077442691. Consultado el 20 de febrero de 2018.
- ↑ a b Fisica Volumen i. Pearson Educación. 2006. ISBN 9789702607762. Consultado el 20 de febrero de 2018.
- ↑ Tipler, Paul Allen; Mosca, Gene (2005). Física para la ciencia y la tecnología. Reverte. ISBN 9788429144116. Consultado el 20 de febrero de 2018.
- ↑ a b c Koetsier, Teun (2010). «Simon Stevin and the rise of Archimedean mechanics in the Renaissance». The Genius of Archimedes – 23 Centuries of Influence on Mathematics, Science and Engineering: Proceedings of an International Conference Held at Syracuse, Italy, June 8–10, 2010. Springer. pp. 94-99. ISBN 978-90-481-9090-4.
- ↑ Devreese, Jozef T.; Guido Vanden Berghe (2008). 'Magic is no magic': The wonderful world of Simon Stevin. WIT Press. pp. 136-139. ISBN 978-1-84564-391-1.
- ↑ a b Feynman, Richard P.; Robert B. Leighton; Matthew Sands (1963). The Feynman Lectures on Physics, Vol. I. USA: California Inst. of Technology. pp. 4.4-4.5. ISBN 978-0-465-02493-3.
- ↑ E.J.Dijksterhuis: Simon Stevin 1943
- ↑ Therese McGuire, Light on Sacred Stones, in Conn, Marie A.; Therese Benedict McGuire (2007). Not etched in stone: essays on ritual memory, soul, and society. University Press of America. p. 23. ISBN 978-0-7618-3702-2.
- ↑ Dutch, Steven (1999). «Pre-Greek Accomplishments». Legacy of the Ancient World. Prof. Steve Dutch's page, Univ. of Wisconsin at Green Bay. Archivado desde el original el 21 de agosto de 2016. Consultado el 13 de marzo de 2012.
- ↑ Moffett, Marian; Michael W. Fazio; Lawrence Wodehouse (2003). A world history of architecture. Laurence King Publishing. p. 9. ISBN 978-1-85669-371-4.
- ↑ Peet, T. Eric (2006). Rough Stone Monuments and Their Builders. Echo Library. pp. 11-12. ISBN 978-1-4068-2203-8.
- ↑ Thomas, Burke (2005). «Transport and the Inclined Plane». Construction of the Giza Pyramids. world-mysteries.com. Archivado desde el original el 13 de marzo de 2012. Consultado el 10 de marzo de 2012.
- ↑ Isler, Martin (2001). Sticks, stones, and shadows: building the Egyptian pyramids. USA: University of Oklahoma Press. pp. 211–216. ISBN 978-0-8061-3342-3.
- ↑ Sprague de Camp, L. (1990). The Ancient Engineers. USA: Barnes & Noble. p. 43. ISBN 978-0-88029-456-0.
- ↑ a b Karl von Langsdorf (1826) Machinenkunde, quoted in Reuleaux, Franz (1876). The kinematics of machinery: Outlines of a theory of machines. MacMillan. pp. 604.
- ↑ for example, the lists of simple machines left by Roman architect Vitruvius (c. 80 – 15 BCE) and Greek philosopher Herón de Alejandría (c. 10 – 70 CE) consist of the five classical simple machines, excluding the inclined plane. – Smith, William (1848). Dictionary of Greek and Roman antiquities. London: Walton and Maberly; John Murray. p. 722., Usher, Abbott Payson (1988). A History of Mechanical Inventions. USA: Courier Dover Publications. pp. 98, 120. ISBN 978-0-486-25593-4.
- ↑ Heath, Thomas Little (1921). A History of Greek Mathematics, Vol. 2. UK: The Clarendon Press. pp. 349, 433–434.
- ↑ a b c Egidio Festa and Sophie Roux, The enigma of the inclined plane in Laird, Walter Roy; Sophie Roux (2008). Mechanics and natural philosophy before the scientific revolution. USA: Springer. pp. 195-221. ISBN 978-1-4020-5966-7.
- ↑ a b Meli, Domenico Bertoloni (2006). Thinking With Objects: The Transformation of Mechanics in the Seventeenth Century. JHU Press. pp. 35-39. ISBN 978-0-8018-8426-9.
- ↑ a b Boyer, Carl B.; Uta C. Merzbach (2010). A History of Mathematics, 3rd Ed.. John Wiley and Sons. ISBN 978-0-470-63056-3.
- ↑ Usher, Abbott Payson (1988). A History of Mechanical Inventions. Courier Dover Publications. p. 106. ISBN 978-0-486-25593-4.
- ↑ Machamer, Peter K. (1998). The Cambridge Companion to Galileo. London: Cambridge University Press. pp. 47-48. ISBN 978-0-521-58841-6.
- ↑ a b Armstrong-Hélouvry, Brian (1991). Control of machines with friction. USA: Springer. p. 10. ISBN 978-0-7923-9133-3.
- ↑ Meyer, Ernst (2002). Nanoscience: friction and rheology on the nanometer scale. World Scientific. p. 7. ISBN 978-981-238-062-3.
- ↑ a b Handley, Brett; David M. Marshall; Craig Coon (2011). Principles of Engineering. Cengage Learning. pp. 71-73. ISBN 978-1-4354-2836-2.
- ↑ Dennis, Johnnie T. (2003). The Complete Idiot's Guide to Physics. Penguin. pp. 116-117. ISBN 978-1-59257-081-2.
- ↑
- ↑ a b Martin, Lori (2010). «Lab Mech14:The Inclined Plane - A Simple Machine». Science in Motion. Westminster College. Consultado el 8 de septiembre de 2012.
- ↑ Pearson (2009). Physics class 10 - The IIT Foundation Series. New Delhi: Pearson Education India. p. 69. ISBN 978-81-317-2843-7.
- ↑ a b Bansal, R.K (2005). Engineering Mechanics and Strength of Materials. Laxmi Publications. pp. 165-167. ISBN 978-81-7008-094-7.
- ↑ a b This derives slightly more general equations which cover force applied at any angle: Gujral, I.S. (2008). Engineering Mechanics. Firewall Media. pp. 275-277. ISBN 978-81-318-0295-3.
Enlaces externos[editar]
 Wikimedia Commons alberga una categoría multimedia sobre planos inclinados.
Wikimedia Commons alberga una categoría multimedia sobre planos inclinados.
















































