Vector normal

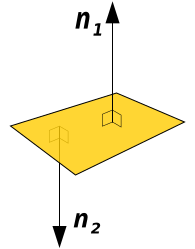
En geometría, un vector normal a una cantidad geométrica (línea, curva, superficie, etc) es un vector de un espacio con producto escalar que contiene tanto a la entidad geométrica como al vector normal, que tiene la propiedad de ser ortogonal a todos los vectores tangentes a la entidad geométrica.

Un vector normal no necesariamente es un vector normalizado o unitario.

En el caso tridimensional, una superficie normal (o simplemente una normal) a un punto P es un vector que es perpendicular al plano tangente a esa superficie en P. La palabra "normal" también se utiliza como adjetivo: una línea normal a un plano, la componente normal de una fuerza, el vector normal, etc. El concepto de normalidad se generaliza a ortogonalidad.^{[cita requerida]}

El concepto ha sido generalizado a variedades diferenciables de dimensión arbitraria encajados en un espacio euclidiano. El espacio vectorial normal, o espacio normal, de una variedad e un punto P es el conjunto de los vectores que son ortogonales al espacio tangente en P. En el caso de curvas diferenciales, el vector de curvatura es un vector normal de interés especial.

La normal es utilizada frecuentemente en graficación de computadoras para determinar la orientación de una superficie hacia una fuente de luz para flat shading, o la orientación de cada una de las esquinas (vértices) para imitar una superficie curveada con sombreado de Phong.

Ejemplo[editar]

En $\scriptstyle \mathbb {R} ^{n}$ el vector normal $\scriptstyle \mathbf {n}$ en un punto a una entidad geométrica tiene la propiedad de que para todo vector del espacio tangente de la entidad en ese punto satisface la relación $\scriptstyle \mathbf {n} \cdot \mathbf {t} =0$