Matemáticas y arte

De Wikipedia, la enciclopedia libre
Matemáticas en el arte: grabado en placa de cobre de Alberto Durero Melancolía I, 1514. Las referencias matemáticas incluyen una brújula para la geometría, un cuadrado mágico y un romboedro truncado, mientras que la medición está indicada por las escalas y el reloj de arena.[1]​
Dibujo alámbrico[2]​ de un vaso como sólido de revolución,[2]​ obra de Paolo Uccello. Siglo XV

Las matemáticas y el arte están relacionados de varias maneras. De hecho, es frecuente encontrar las matemáticas descritas como un arte debido a la belleza o la elegancia de muchas de sus formulaciones, y se puede encontrar fácilmente su presencia en manifestaciones como la música, la danza, la pintura, la arquitectura, la escultura y las artes textiles.

Este artículo se centra en la influencia de las matemáticas en las artes visuales.

Las matemáticas y el arte tienen una larga relación histórica. Está documentada la existencia de artistas matemáticos desde el siglo IV a. C., cuando el escultor griego Policleto escribió su "Canon", prescribiendo proporciones basadas en la relación 1:√2 para el desnudo masculino ideal. Curiosamente, cada vez son más frecuentes presuntas evidencias del uso del número áureo en el arte y la arquitectura antiguos, sin bases fiables que respalden estas teorías. En el Renacimiento italiano, Luca Pacioli escribió el influyente tratado De divina proportione (1509), ilustrado con grabados en madera realizados por Leonardo da Vinci, sobre el uso de la proporción áurea en el arte. Otro pintor italiano, Piero della Francesca, desarrolló las ideas de Euclides sobre la perspectiva en tratados como De Prospectiva Pingendi y en sus propias pinturas. El grabador Alberto Durero efectuó numerosas referencias a las matemáticas en su obra, con trabajos como Melancolía I. En los tiempos modernos, el artista gráfico M. C. Escher hizo un uso intensivo del teselado y de la geometría hiperbólica con la ayuda del matemático Harold Scott MacDonald Coxeter, mientras que el movimiento De Stijl liderado por Theo van Doesburg y Piet Mondrian abarcó explícitamente las formas geométricas. Las matemáticas han inspirado las artes textiles tales como el quilting, el punto, el punto de cruz, el ganchillo, el bordado, la tejeduría, las alfombras y otras creaciones como el kilim. En el arte islámico, las simetrías son evidentes en formas tan variadas como el girih persa y el azulejo zellige marroquí, las pantallas mogolas jali de piedra perforada y las bóvedas decoradas con mocárabe.

El influjo directo de las matemáticas sobre el arte se evidencia en el uso de herramientas conceptuales como la perspectiva, el análisis de la simetría y en la presencia en diversas obras de objetos matemáticos que han ejercido una especial atracción sobre artistas de distintas épocas, como los poliedros o la banda de Möbius. Magnus Wenninger creó poliedros estrellados coloridos, originalmente como modelos para la enseñanza.

Conceptos matemáticos como recursión y paradojas lógicas se pueden ver en las pinturas de René Magritte y en grabados de M. C. Escher. El arte computacional a menudo hace uso de fractales, incluido el conjunto de Mandelbrot, y, a veces, explora otros objetos matemáticos como los autómatas celulares. De forma controvertida, ligando la óptica con la pintura, el artista David Hockney ha argumentado que desde el Renacimiento en adelante la mayoría de los artistas utilizaron la cámara lúcida para dibujar representaciones precisas de escenas; y el arquitecto Philip Steadman argumentó de manera similar que Johannes Vermeer usó la cámara oscura en la composición de sus pinturas.

Otras relaciones incluyen el análisis algorítmico de las obras de arte mediante la fluorescencia de rayos X, o el hallazgo de que los batik tradicionales de diferentes regiones de la isla de Java tienen composiciones fractales. El arte ha servido en ocasiones como estímulo para la investigación matemática, especialmente en el caso de la teoría de la perspectiva de Filippo Brunelleschi, que finalmente llevó a Girard Desargues al desarrollo de la geometría proyectiva. Una visión persistente, basada en última instancia en la noción pitagórica de armonía en la música, sostiene que el universo está organizado según relaciones numéricas, que Dios es el geómetra del mundo y que, por lo tanto, la geometría es sagrada, tal como queda reflejado en obras de arte como El anciano de los días de William Blake.

Orígenes: desde la antigua Grecia hasta el Renacimiento[editar]

Canon y simetría de Policleto[editar]

Copia romana en mármol del Doríforo, originalmente un bronce obra de Policleto
Artículo principal: Policleto

Policleto el mayor (c. 450–420 a. C.) fue un escultor griego de la escuela de Argos, contemporáneo de Fidias. La temática de sus estatuas de bronce consistía principalmente en atletas. Según el filósofo y matemático Jenócrates, Policleto está clasificado como uno de los escultores más importantes de la antigüedad clásica por su trabajo en el Doríforo y en la estatua de Hera en el Hereo de Argos.[3]​ Mientras que sus esculturas pueden no ser tan famosas como las de Fidias, también son muy admiradas. En su "Canon", un tratado que escribió para documentar las proporciones "perfectas" de la anatomía del desnudo masculino, Policleto introdujo un enfoque matemático para esculpir el cuerpo humano.[3]​

Utilizaba la longitud de la falangeta del meñique de la mano como el módulo básico para determinar las proporciones del cuerpo humano.[4]​ Policleto multiplicaba la longitud de la falangeta por la raíz cuadrada de dos (√2) para obtener la distancia de la segunda falange (falangina) y multiplicaba la longitud nuevamente por √2 para obtener la longitud de la tercera falange. A continuación, tomaba la longitud del meñique y la multiplica por √2 para obtener la longitud de la palma desde la base del dedo hasta el cúbito. Esta serie geométrica de medidas avanza hasta formar el brazo, el tórax y el cuerpo completo con todas sus partes.[5]​

La influencia del "Canon" de Policleto es inmensa en la escultura de la antigua Grecia, Roma y el Renacimiento, y numerosos escultores siguieron sus prescripciones. Si bien no se conserva ninguna de las obras originales de Policleto, las copias romanas muestran su ideal de perfección física y precisión matemática. Algunos estudiosos argumentan que el pensamiento pitagórico influyó en el "Canon" de Policleto,[6]​ donde se aplican los conceptos matemáticos básicos de la geometría griega, como la relación, la proporción y la simetría (en griego significa "armonía en las proporciones") y los convierte en un sistema capaz de describir la forma humana a través de una serie de progresiones geométricas continuas.[4]​

Perspectiva y proporción[editar]

Artículo principal: Perspectiva
Experimento de Brunelleschi sobre la perspectiva

En la antigüedad clásica, en lugar de ajustar el tamaño de las figuras de una composición de acuerdo con su distancia al observador (según las reglas de la perspectiva), los pintores establecían el tamaño de objetos y figuras según su importancia temática. En la Edad Media, algunos artistas usaron la perspectiva invertida para dar un énfasis especial a determinados motivos. El matemático musulmán Alhacén (Ibn al-Haytham) describió una teoría geométrica de la óptica en su "Libro de Óptica" en 1021, pero nunca la aplicó al arte.[7]​ El Renacimiento vio el resurgir de las ideas griegas y romanas clásicas en la cultura, incluido el estudio de las matemáticas para comprender la naturaleza y el arte. Dos motivos principales llevaron a los artistas de finales de la Edad Media y del Renacimiento hacia las matemáticas: en primer lugar, los pintores necesitaban descubrir cómo representar escenas tridimensionales en un lienzo bidimensional; y en segundo lugar, tanto los filósofos como los artistas estaban convencidos de que las matemáticas eran la verdadera esencia del mundo físico y que todo el universo, incluidas las artes, podía explicarse en términos geométricos.[8]​

Los rudimentos de la perspectiva llegaron con Giotto (1266/7-1337), que intentó dibujar en perspectiva utilizando un método algebraico para determinar la ubicación de las líneas distantes. En 1415, el arquitecto italiano Filippo Brunelleschi y su amigo Leon Battista Alberti demostraron en Florencia el método geométrico necesario para aplicar la perspectiva, utilizando el principio de semejanza tal como lo formuló Euclides para determinar la altura aparente de objetos distantes.[9]​[10]​ Aunque se han perdido las pinturas en perspectiva de Brunelleschi, los frescos de Masaccio de la Santísima Trinidad muestra sus principios en funcionamiento.[7]​[11]​[12]​

Paolo Uccello utilizó la perspectiva de forma innovadora en la Batalla de San Romano (c. 1435–1460)

El pintor italiano Paolo Uccello (1397-1475) estaba fascinado por la perspectiva, como se muestra en sus pinturas de la Batalla de San Romano (c. 1435–1460): las lanzas rotas convergen convenientemente según líneas de perspectiva.[13]​[14]​

El pintor Piero della Francesca (c. 1415–1492) ejemplificó este nuevo cambio en el pensamiento del Renacimiento italiano, aunando su condición de artista con la de experto matemático y geómetra, autor de libros sobre la geometría del espacio y la perspectiva, incluyendo De Prospectiva pingendi (Sobre la perspectiva para pintar), Trattato d'Abaco (Tratado del Ábaco), y De corporibus regularibus (Sobre los Sólidos Regulares).[15]​[16]​[17]​

El historiador Giorgio Vasari en su obra Las vidas de los más excelentes arquitectos, pintores y escultores italianos llama a Piero el "geómetra más grande de su tiempo, o quizás de cualquier época".[18]​ El interés de Piero della Francesca por la perspectiva se puede ver en sus pinturas, incluyendo el Políptico de San Antonio,[19]​ el Retablo de San Agostino y Cristo en la columna. Su trabajo sobre geometría influyó en matemáticos y artistas posteriores, incluido Luca Pacioli en su obra De divina proportione y sobre Leonardo da Vinci. Estudió matemáticas clásicas y los trabajos de Arquímedes,[20]​ y aprendió aritmética comercial en "escuelas del ábaco". El formato de sus escritos recuerda al de los libros de texto de la escuela del ábaco,[21]​ siguiendo muy posiblemente el estilo del influyente Liber abaci, publicado en 1202 por Leonardo de Pisa (Fibonacci). La irrupción de la perspectiva lineal en el mundo artístico ya era un hecho. Alberti explicó en su tratado de 1435 De pictura que: "Los rayos de luz viajan en línea recta desde los puntos en la escena observada hasta el ojo, formando una especie de pirámide con el ojo como vértice". Una pintura construida mediante la perspectiva lineal es una sección transversal de esa pirámide.[22]​

En "De Prospectiva Pingendi", Piero transformó sus observaciones empíricas de la forma en que los aspectos de una figura cambian con el punto de vista en pruebas matemáticas. Su tratado parte del trabajo de Euclides: define el punto como "la cosa más pequeña que es posible que el ojo comprenda".[23]​[8]​ Utiliza el razonamiento deductivo para guiar al lector a la representación en perspectiva de un cuerpo tridimensional.[24]​

El artista David Hockney argumentó en su libro Conocimiento secreto: redescubriendo las técnicas perdidas de los antiguos maestros que los artistas comenzaron a usar una cámara lúcida a partir de la década de 1420, lo que dio como resultado un cambio repentino en la precisión y en el realismo, y que esta práctica fue continuada por los principales artistas, incluidos Ingres, Van Eyck y Caravaggio.[25]​ Los críticos no se ponen de acuerdo en si la tesis de Hockney es correcta.[26]​[27]​ Del mismo modo, el arquitecto Philip Steadman argumentó de manera controvertida[28]​ que Johannes Vermeer había usado un dispositivo diferente, una cámara oscura, para ayudarle a crear sus pinturas con su distintiva forma de observación de los motivos representados.[29]​

Rombicuboctaedro hueco en perspectiva, obra de Leonardo

En 1509, Luca Pacioli (c. 1447-1517) publicó De divina proportione sobre la relación de las matemáticas y el arte a través de la proporción, abordando incluso por este método cuestiones como la representación del rostro humano. Leonardo da Vinci (1452–1519) ilustró el texto con grabados de sólidos regulares mientras estudiaba con Pacioli en la década de 1490. Los dibujos de Leonardo son probablemente las primeras ilustraciones realistas de sólidos geométricos reducidos a un armazón de gruesas aristas.[30]​ Figuras como el rombicuboctaedro fueron de las primeras en ser dibujadas de esta manera para demostrar la perspectiva, mediante la superposición de las aristas situadas en primer plano sobre las del fondo, que podían a su vez verse por los huecos de las caras. El trabajo discute la perspectiva en los trabajos de Piero della Francesca, Melozzo da Forlì y Marco Palmezzano.[31]​

Da Vinci estudió la "Summa" de Pacioli, de la que copió las tablas de proporciones.[32]​ En La Gioconda y en La Última Cena, incorporó una perspectiva lineal con un punto de fuga para obtener una apariencia de profundidad.[33]​ La Última Cena se ideó con una proporción estrecha de 12:6:4:3, al igual que la La escuela de Atenas de Rafael, que incluye a Pitágoras con unas tablas de proporciones ideales, sagradas para los pitagóricos.[34]​[35]​ En el Hombre de Vitruvio, Leonardo expresó las ideas del arquitecto romano Vitruvio, mostrando de manera innovadora la figura masculina, centrándola en un círculo y en un cuadrado.[36]​

Ya en el siglo XV, la perspectiva curvilínea encontró su camino en las pinturas de artistas interesados en las distorsiones de la imagen. El Retrato de Giovanni Arnolfini y su esposa, pintado por Jan van Eyck en 1434, contiene un espejo convexo con reflejos de las personas en la escena,[37]​ mientras que Parmigianino, en su Autorretrato en un espejo convexo (c. 1523–1524), muestra la cara casi sin distorsión del artista en el centro, con un fondo muy curvado y la mano del artista alrededor del borde.[38]​

El espacio tridimensional puede representarse de manera convincente en el arte, como en el dibujo técnico, por medios distintos a la perspectiva. Los sistemas de proyección oblicua, incluida la perspectiva caballera (utilizada por artistas militares franceses para representar fortificaciones en el siglo XVIII), fueron utilizados de forma continua y ubicua por artistas chinos desde el primer o segundo siglo hasta el siglo XVIII. Los chinos adquirieron la técnica de la India, que la adquirió de la Antigua Roma. La proyección oblicua también aparece en el arte japonés, como en las pinturas Ukiyo-e de Torii Kiyonaga (1752–1815).[39]​

Relación de oro[editar]

Artículo principal: Sección áurea

El número áureo (aproximadamente igual a 1.618) ya era conocido por Euclides.[40]​ La proporción áurea ha sido reivindicada de forma persistente[41]​[42]​[43]​[44]​ en tiempos modernos por su presunta utilización en el arte y especialmente en la arquitectura del antiguo Egipto, Grecia y otras culturas sin evidencias fiables.[45]​

Esta situación puede derivar en parte de la confusión de la "relación áurea" con la "media dorada", que para los griegos antiguos significaba "evitar el exceso en cualquier dirección", no una relación geométrica.[45]​ Desde el siglo XIX, numerosos expertos y aficionados a la piramidología han argumentado utilizando dudosos razonamientos matemáticos para hallar la proporción de oro en el diseño de las pirámides.[46]​[45]​[47]​[48]​ Se ha afirmado que Partenón, un templo del siglo V a. C. en Atenas, se utiliza la proporción áurea en su fachada y en su plano de planta,[49]​[50]​[51]​ pero estas afirmaciones también son refutadas por las medidas reales del monumento.[45]​

La Gran Mezquita de Kairuán en Túnez también se ha afirmado que utilizó la proporción áurea en su diseño,[52]​ pero la citada proporción no aparece en las partes originales de la mezquita.[53]​ El historiador de la arquitectura Frederik Macody Lund argumentó en 1919 que la Catedral de Chartres (siglo XIII), la Catedral de Laon (1157-1205) y la Catedral de Notre Dame (París) (1160) están diseñados de acuerdo con el número áureo,[54]​ dibujando líneas auxiliares para demostrar su tesis. Otros estudiosos argumentan que hasta el trabajo de Pacioli en 1509, la proporción de oro era desconocida para los artistas y arquitectos.[55]​ Por ejemplo, la altura y el ancho de la parte delantera de Notre-Dame de Laon tienen la proporción 8/5 o 1.6, no 1.618. Tales términos de la sucesión de Fibonacci se convierten rápidamente en difíciles de distinguir de la proporción áurea.[56]​ Después de Pacioli, la proporción áurea es más perceptible en las obras de arte, incluida La Gioconda de Leonardo.[57]​

Otro número morfológico del que se ha escrito abundantemente es el número plástico,[58]​[59]​ ideado en 1928 por el arquitecto holandés Hans van der Laan (originalmente llamado en francés "le nombre radiant", el número radiante).[60]​ Su valor es la solución de la ecuación cúbica

,

un número irracional que es aproximadamente 1.325. Según el arquitecto Richard Padovan, esta conectado con las fracciones características 3/4 y 1/7, que gobiernan los límites de la percepción humana al relacionar un tamaño físico con otro. Van der Laan usó estas proporciones al diseñar la iglesia de St. Benedictusberg Abbey (1967) en los Países Bajos.[60]​


[1]

[2]

[3]

[4]

Simetrías planas[editar]

Véanse también: Simetría, Grupo del papel pintado, Patrones geométricos islámicos y Kilim.
Presencia poderosa:[61]​ alfombra con doble medallón. Anatolia Central (Konya-Karapınar), paso del siglo XVI al XVII. Mezquita Alâeddin

Las simetrías en el plano se han utilizado durante milenios en obras de arte como alfombras, celosías, textiles y todo tipo de adornos.[62]​[63]​[64]​[65]​

Muchas alfombras tradicionales, ya sean de pelo o del tipo kilim de tejido plano, se dividen en un campo central y un borde de encuadre. Ambos pueden presentar simetrías, aunque en las alfombras tejidas a mano a menudo están ligeramente alteradas por pequeños detalles, variaciones de patrón y cambios de color introducidos por el tejedor.[62]​ En los kilims de Anatolia, los motivos utilizados son generalmente simétricos. En el diseño general también suele estar presente la simetría, con configuraciones tales como franjas, franjas alternas con filas de motivos, y arreglos agrupados de motivos aproximadamente hexagonales. El campo se presenta comúnmente como un fondo asimilable a un patrón del grupo del papel pintado de configuración pmm, mientras que el borde toma la forma de un friso del tipo pm11, pmm2 o pma2. Los kilims turcos y de Asia central a menudo tienen tres o más fronteras entre diferentes grupos de frisos. Es obvio que los tejedores ciertamente buscaban la simetría, sin el conocimiento explícito de sus matemáticas.[62]​

El matemático y teórico de la arquitectura Nikos Salingaros sugiere que la "poderosa presencia"[61]​ (efecto estético) de una "gran alfombra",[61]​ como las mejores alfombras de dos medallones Konya del siglo XVII, se crean mediante técnicas matemáticas relacionadas con las teorías del arquitecto Christopher Alexander. Estas técnicas incluyen introducir zonas de color como pares opuestos; diferenciar áreas geométricamente, ya sea utilizando formas complementarias o equilibrando la direccionalidad de los ángulos agudos; utilizar la complejidad a pequeña escala (desde el nivel de nudo hacia arriba) y la simetría a pequeña y a gran escala; y la utilización de elementos repetidos en una jerarquía de diferentes escalas (con una relación de aproximadamente 2.7 de cada nivel al siguiente). Salingaros sostiene que "todas las alfombras consideradas artísticas satisfacen al menos nueve de las diez reglas anteriores", y sugiere que podría ser posible crear una métrica a partir de estas reglas.[61]​

Elaborados enrejados se encuentran en los trabajos de la India denominados jali, tallados en mármol para adornar tumbas y palacios.[63]​ Las celosías chinas, siempre con cierta simetría, existen en 14 de los 17 grupos de simetría planar; a menudo presentan simetría de espejo, de doble espejo o simetría rotacional. Algunas presentan un medallón central y otras incluyen un borde con un friso.[66]​ Muchas celosías chinas han sido analizadas matemáticamente por Daniel S. Dye, que ha identificado Sichuan como el centro de este arte.[67]​

Dovelas girih

Las simetrías tienen un papel muy destacado en las artes textiles, incluyendo el quilting,[64]​ el punto,[68]​ el punto de cruz, el ganchillo,[69]​ los bordados[70]​[71]​ y los distintos tipos de tejeduría,[72]​ donde estos patrones pueden ser puramente decorativos o pueden indicar el estatus de su propietario.[73]​ La simetría rotacional se encuentra en estructuras circulares tales como cúpulas, en ocasiones elaboradamente decoradas con patrones simétricos por dentro y por fuera, como en la Mezquita del jeque Lotf Allah de Isfahán (1619).[74]​ Los artículos de bordado y encaje como manteles y tapetes de mesa, hechos con bobinas o con bolillos, pueden tener una amplia variedad de reflexiones y rotaciones simétricas, que han sido exploradas matemáticamente.[75]​

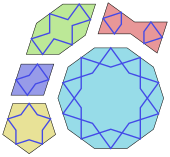
En el arte islámico, los patrones geométricos están presentes en muchas de sus formas de arte, especialmente en los embaldosados girih. Estos teselados se forman utilizando un conjunto de cinco formas de baldosas, a saber: un decágono regular, un hexágono alargado, una pajarita, un rombo y un pentágono regular. Todos los lados de estos azulejos tienen la misma longitud; y todos sus ángulos son múltiplos de 36° (π/5 radianes), mostrando simetrías de cinco y diez módulos. Las baldosas están decoradas con líneas de lacería en relieve (girih), generalmente más visibles que los límites de las baldosas. En 2007, los físicos Peter Lu y Paul Steinhardt argumentaron que el enlosado girih era similar al cuasicristal definido por la teselación de Penrose.[76]​ Las baldosas geométricas elaboradas con pequeñas teselas (zellige) son un elemento distintivo en la arquitectura de Marruecos.[65]​ Las bóvedas decoradas con mocárabe son tridimensionales, pero están diseñadas en dos dimensiones con dibujos de celdas geométricas.[77]​

Poliedros[editar]

Retrato de Luca Pacioli disertando sobre los poliedros, atribuido a Jacopo de'Barbari (1495)

Los sólidos platónicos y otros poliedros son un tema recurrente en el arte occidental. Se encuentran, por ejemplo, en un mosaico de mármol donde aparece un pequeño dodecaedro estrellado atribuido a Paolo Uccello y que forma parte del suelo de la Basílica de San Marcos en Venecia;[13]​ en los diagramas de poliedros regulares de Leonardo da Vinci dibujados como ilustraciones para el libro 1509 de Luca Pacioli De Divina Proportione;[13]​ como un rombicuboctaedro de cristal en el retrato de Pacioli de Jacopo de' Barbari, pintado en 1495;[13]​ y en el poliedro truncado (y varios otros objetos matemáticos) que aparecen en el grabado de Alberto Durero titulado Melancolía I.[13]​

Alberto Durero (1471-1528) fue un artista alemán del Renacimiento, que hizo importantes contribuciones al estudio de los poliedros en su libro de 1525, Underweysung der Messung (Educación sobre la medición), destinado a la enseñanza de la perspectiva, la geometría en arquitectura, los sólidos platónicos, y los polígonos regulares. Durero probablemente estuvo influenciado por los trabajos de Piero della Francesca y Luca Pacioli durante sus viajes a Italia.[78]​ Mientras que los ejemplos de perspectiva en "Underweysung der Messung" están poco desarrollados y contienen imprecisiones, el texto contiene una discusión detallada sobre los poliedros. Durero es también el primero en introducir en el texto la idea del desarrollo de un poliedro,[79]​ incluyendo poliedros desplegados para que queden planos para su impresión. Durero publicó en 1528 otro libro influyente sobre las proporciones del cuerpo humano,[80]​ titulado "Vier Bücher von Menschlicher Proportion (Cuatro libros sobre la proporción humana)".

El conocido grabado de Durero titulado Melancolía I, representa a un ser alado, sentado en actitud pensativa. La imagen incluye un cuadrado mágico y un trapezoedro triangular truncado.[1]​ Estos dos elementos, y el grabado en su conjunto, han sido objeto de más interpretaciones modernas que casi cualquier otra obra comparable,[81]​[82]​[83]​ incluyendo un libro de dos volúmenes de Peter-Klaus Schuster, y un influyente análisis contenido en la monografía de Erwin Panofsky sobre Durero.[1]​[84]​

Otro famoso pintor que incluyó poliedros en algunas de sus pinturas es el español Salvador Dalí. En su cuadro titulado La Última Cena, Cristo y sus discípulos están representados dentro de un dodecaedro gigante. Otra de sus obras, la Crucifixión (1954),[85]​ muestra un hipercubo desplegado, que hace alusión a la perspectiva divina en cuatro dimensiones.[86]​[87]​

Dimensiones fractales[editar]

Un batik, tejido tradicional procedente de Surakarta, Java, como este parang klithik con patrón de espadas, tiene una dimensión fractal de entre 1.2 y 1.5

Los diseños tradicionales de batik, teñidos en Indonesia mediante el procedimiento de reserva con cera, combinan motivos figurativos (como elementos florales y vegetales) con motivos abstractos y algo caóticos, incluida la imprecisión derivada de la aplicación de la reserva de cera, y la variación aleatoria introducida por el agrietamiento de la propia cera. Los diseños de batik tienen una dimensión fractal de entre 1 y 2, que varía en diferentes estilos regionales. Por ejemplo, el batik de Cirebon tiene una dimensión fractal de 1.1; los batiks de Yogyakarta y Surakarta (la ciudad de Solo) en el centro de Java tienen una dimensión fractal de 1.2 a 1.5; y los batiks de Lasem en la costa norte de Java y de Tasikmalaya en Java occidental, tienen una dimensión fractal de entre 1.5 y 1.7.[88]​

Las obras de dripping del artista moderno Jackson Pollock son igualmente distintivas por su dimensión fractal. Su obra titulada Número 14 de 1948 tiene una dimensión de 1.45, mientras que sus pinturas posteriores tuvieron dimensiones fractales sucesivamente más altas y, por consiguiente, patrones más elaborados. Una de sus últimas obras, Blue Poles, le llevó seis meses de trabajo, y tiene una dimensión fractal de 1.72.[89]​

Una relación compleja[editar]

El astrónomo Galileo Galilei en su obra "El ensayador" escribió que "[El universo] está escrito en el lenguaje de las matemáticas, y sus caracteres son triángulos, círculos y otras figuras geométricas". Los artistas[90]​ que se esfuerzan y buscan estudiar la naturaleza, según Galileo, deben primero ver y entender completamente las matemáticas.

Sin embargo, los matemáticos han tratado de interpretar y analizar el arte a través de la lente de la geometría y de la racionalidad. El matemático Felipe Cucker sugiere que las matemáticas, y especialmente la geometría, son una fuente de reglas para la "creación artística impulsada por reglas", aunque no la única.[91]​ Algunas de las muchas cadenas de la compleja relación resultante[92]​ se describen a continuación.

El matemático Godfrey Harold Hardy definió un conjunto de criterios para calificar la belleza matemática

Las matemáticas como arte[editar]

Artículo principal: Belleza matemática

El matemático Jerry P. King describe las matemáticas como un arte, afirmando que "las claves de las matemáticas son la belleza y la elegancia y no el aburrimiento y los tecnicismos", y que la belleza es la fuerza motivadora de la investigación matemática.[93]​ King cita el ensayo matemático publicado por Godfrey Harold Hardy en 1940, titulado Apología de un matemático. En este escrito, Hardy analiza por qué encuentra dos teoremas de la antigüedad clásica como de primera clase, a saber, la prueba de Euclides de que hay infinitos números primos, y la prueba de que la raíz cuadrada de 2 es un número irracional. King evalúa estos teoremas según los criterios de Hardy para estimar la elegancia matemática: "sobriedad, profundidad, generalidad, imprevisibilidad, inevitabilidad" y "economía" (las cursivas son de King), y describe la prueba como "estéticamente agradable".[94]​ El matemático húngaro Paul Erdős estuvo de acuerdo en que las matemáticas poseían belleza, pero consideró las razones más allá de la explicación: "¿Por qué son hermosos los números? Es como preguntar por qué es hermosa la Novena Sinfonía de Beethoven. Si no ves el porqué, nadie te lo puede explicar. Yo sé que los números son hermosos".[95]​

Herramientas matemáticas para el arte[editar]

Octopod, obra de Mikael Hvidtfeldt Christensen. Arte algorítmico producido con el programa Structure Synth
Véanse también: Anexo:Lista de artistas matemáticos, Fractalismo y Arte computacional.

Las matemáticas aparecen en el sustrato de prácticamente todas las artes, como la música, la danza,[96]​ la pintura, la arquitectura y la escultura.

Cada una está asociado con las matemáticas de una manera particular.[97]​ Gracias a su conexión con las artes visuales, las matemáticas pueden proporcionar herramientas para los artistas, como las reglas de la perspectiva descritas por Brook Taylor y Johann Heinrich Lambert, o los métodos de geometría descriptiva, posteriormente aplicados al modelado de sólidos por ordenador, y cuyos orígenes teóricos se remontan a Durero y a Gaspard Monge.[98]​

Los artistas de la Edad Media y del Renacimiento (como Luca Pacioli, Leonardo da Vinci y Durero) han utilizado y desarrollado ideas matemáticas mientras investigaban nuevas formas de llevar a cabo su trabajo artístico.[97]​[99]​ El uso de la perspectiva comenzó, a pesar de algunos intentos incipientes en la arquitectura de la antigua Grecia, con los pintores italianos como Giotto en el siglo XIII; reglas como la del punto de fuga fueron formuladas por primera vez por Filippo Brunelleschi alrededor de 1413,[7]​ y sus teorías influyeron definitivamente en Leonardo y en Durero.

El trabajo de Isaac Newton sobre el espectro óptico influyó en la teoría de los colores de un literato como Goethe y, a su vez, en artistas como Philipp Otto Runge, J. M. W. Turner,[100]​ los miembros de la Hermandad Prerrafaelita y sobre Vasili Kandinski.[101]​[102]​

Los artistas también pueden analizar la simetría de una escena, y trabajar sobre este concepto. Las mismas herramientas[103]​ pueden ser aplicadas por matemáticos que están explorando el arte, o por artistas inspirados en las matemáticas, como M. C. Escher (inspirado en Harold Scott MacDonald Coxeter) o el arquitecto Frank Gehry, quien argumentó que el diseño asistido por computadora le permitió expresarse de una manera completamente nueva.[104]​

El artista Richard Wright argumenta que los objetos matemáticos que pueden construirse pueden verse "como procesos para simular fenómenos" o como obras de "arte computacional". Considera la naturaleza del pensamiento matemático, observando que los matemáticos conocían los fractales desde un siglo antes de que fueran reconocidos como tales. Wright concluye afirmando que es apropiado someter los objetos matemáticos a cualquier método utilizado para "llegar a un acuerdo con conceptos culturales como el arte, la tensión entre objetividad y subjetividad, sus significados metafóricos y el carácter de los sistemas de representación". Da como ejemplos una imagen del conjunto de Mandelbrot, una imagen generada por un algoritmo de autómata celular y una imagen renderizada, y discute, con referencia al Test de Turing, si los productos de un algoritmo pueden ser arte.[105]​ Sasho Kalajdzievski, en su obra "Math and Art: An Introduction to Visual Mathematics (Matemáticas y Arte: una introducción a las matemáticas visuales) adopta un enfoque similar, analizando temas matemáticos visuales adecuados, como teselados, fractales y geometría hiperbólica.[106]​

Algunas de las primeras obras de arte computacional fueron creadas por "Drawing Machine 1", un sistema ideado por Desmond Paul Henry, que consistía en una computadora analógica basada en un visor de bombardero, exhibida en 1962.[107]​[108]​ La máquina era capaz de crear dibujos lineales complejos, abstractos, asimétricos o curvilíneos, pero repetitivos.[107]​[109]​ Más recientemente, Hamid Naderi Yeganeh ha creado formas sugerentes de objetos del mundo real, como peces y aves, utilizando fórmulas que son sucesivamente variadas para dibujar familias de curvas o líneas en ángulo.[110]​[111]​[112]​ Artistas como Mikael Hvidtfeldt Christensen crean obras de arte algorítmico escribiendo rutinas para un sistema de software como Structure Synth: el artista dirige efectivamente el sistema para aplicar una combinación deseada de operaciones matemáticas a un conjunto de datos previajente elegido.[113]​[114]​

De las matemáticas al arte[editar]

Véanse también: Protocubismo, Teselación, M. C. Escher, Origami y Matemáticas y artes del tejido.
Theo van Doesburg: Seis Momentos en el Desarrollo del Plano al Espacio, 1926 o 1929

El matemático y físico teórico Henri Poincaré, autor de Ciencias e Hipótesis, fue leído ampliamente por los cubistas, incluyendo a Pablo Picasso y a Jean Metzinger.[115]​[116]​ Poincaré veía la geometría euclidiana como una de las muchas configuraciones posibles del espacio, en lugar de como una verdad objetiva absoluta. Picasso, en su obra de 1907 Las señoritas de Avignon utilizó la proyección en una cuarta dimensión para mostrar simultáneamente las figuras de frente y de perfil.[117]​

La posible existencia de una cuarta dimensión inspiró a los artistas la posibilidad de cuestionar la perspectiva clásica heredada del Renacimiento: la geometría no euclidiana se convirtió en una alternativa válida más.[118]​[119]​[120]​ El concepto de que la pintura podría expresarse matemáticamente, en color y forma, contribuyó al cubismo, el movimiento artístico que condujo al arte abstracto.[121]​ Metzinger, en 1910, escribió que "[Picasso] presenta una perspectiva móvil y gratuita, desde la que ese ingenioso matemático, Maurice Princet, ha deducido toda una geometría".[122]​ Más adelante, escribió en sus memorias:

Maurice Princet nos reunía frecuentemente ... era un artista que conceptualizaba las matemáticas, e invocaba un continuo n-dimensional con pretensiones estéticas. Le encantaba ver cómo los artistas se interedaban en las nuevas visiones espaciales desarrolladas por Schlegel y otros matemáticos. Tuvo éxito en este cometido.[123]​

El impulso de hacer modelos de enseñanza o investigación de formas matemáticas crea naturalmente objetos que tienen simetrías y formas sorprendentes o agradables. Algunos de estos objetos han inspirado a artistas como los dadaistas Man Ray[124]​ Marcel Duchamp[125]​ y Max Ernst,[126]​[127]​ y tras Man Ray, a Hiroshi Sugimoto.[128]​

Retrato de Joella. Man Ray y Salvador Dalí (Museo Reina Sofía)

Man Ray fotografió algunos de los modelos matemáticos conservados en el Institut Henri Poincaré en París, incluyendo "Objet Matemathique" (Objeto Matemático). Señaló que representaba superficies de Enneper con curvatura constante, derivadas de una pseudoesfera. Este fundamento matemático era importante para él, ya que le permitía negar que el objeto era "abstracto", permitiéndole afirmar que era tan real como el orinal que Duchamp convirtió en una obra de arte. Admitió que la fórmula de la superficie de Enneper que definía el objeto "no significaba nada para mí, pero las formas en sí mismas eran tan variadas y auténticas como cualquier otra en la naturaleza". Utilizó sus fotografías de los modelos matemáticos como figuras de su serie sobre las obras de William Shakespeare, como su pintura "Antony and Cleopatra" de 1934.[129]​ El reportero de arte Jonathan Keats, en un artículo de la revista "ForbesLife", sostiene que Man Ray fotografió "los paraboloides elípticos y los puntos cónicos con la misma luz sensual que sus imágenes de Alice Prin", y "replantea ingeniosamente los cálculos geniales de las matemáticas para revelar la topología del deseo".[130]​ tomaron escultores del siglo XX como Henry Moore, Barbara Hepworth y Naum Gabo inspiración de los modelos matemáticos.[131]​ Moore escribió sobre su Madre e hijo con cuerdas de 1938: "Sin duda, la fuente de mis figuras con cuerdas fue el Museo de Ciencias de Londres ... Me fascinaron los modelos matemáticos que vi allí ... "no fue el estudio científico de estos modelos, sino la capacidad de mirar a través de las cuerdas como en una jaula de pájaros y de ver una forma dentro de otra, lo que me emocionó".[132]​

Los artistas Theo van Doesburg y Piet Mondrian fundaron el movimiento De Stijl, que pretendía "establecer un vocabulario visual de formas geométricas elementales comprensibles por todos y adaptables a cualquier disciplina".[133]​[134]​ Muchas de sus obras de arte consisten visiblemente en cuadrados y triángulos, a veces también con círculos. Los artistas de De Stijl trabajaron en pintura, mobiliario, diseño de interiores y arquitectura.[133]​ Después de la separación de De Stijl, Van Doesburg fundó el movimiento vanguardista Art Concret, describiendo su obra de finales de la década de 1920 tituladaSeis Momentos en el Desarrollo del Plano al Espacio, como una serie de cuatro cuadrados negros sobre la diagonal de un fondo cuadrado, como "una estructura que se puede controlar, una superficie definida sin elementos aleatorios ni capricho individual", pero "No le falta espíritu, no le falta lo universal y no ... vacío, ya que posee un todo que se ajusta al ritmo interno". La crítica de arte Gladys Fabre observó que hay dos progresiones trabajando en la pintura, a saber, los cuadrados negros en crecimiento y los fondos alternos.[135]​

Las matemáticas del teselado, los poliedros, la configuración del espacio y la autorreferencia proporcionaron al artista gráfico M. C. Escher (1898-1972) material de por vida para sus grabados en madera.[136]​[137]​ En el Boceto de la Alhambra, Escher demostró que es posible crear arte con polígonos o formas regulares como triángulos, cuadrados y hexágonos. También usó polígonos irregulares para teselar el plano y a menudo utilizó reflexiones y traslaciones para obtener patrones adicionales. Muchas de sus obras contienen construcciones imposibles, hechas con objetos geométricos que configuran una contradicción entre la proyección en perspectiva y las tres dimensiones, pero son agradables a la vista humana. Su grabado "Ascendente y Descendente" se basa en la "escalera imposible" creada por el científico Lionel Sharples Penrose y su hijo el matemático Roger Penrose.[138]​[139]​[140]​

Algunos de los muchos dibujos de teselado de Escher se inspiraron en conversaciones con el matemático Harold Scott MacDonald Coxeter sobre la geometría hiperbólica.[141]​ Escher estaba especialmente interesado en cinco poliedros específicos, que aparecen muchas veces en su trabajo. Los sólidos platónicos (tetraedros, cubos, octaedros, dodecaedros e icosaedros) aparecen especialmente destacados en "Orden y Caos" y "Cuatro Sólidos Regulares".[142]​ Estas figuras a menudo se sitúan dentro de otras formas que distorsionan aún más el ángulo de visión y la conformación de los poliedros, proporcionando una obra de arte en perspectiva multifacética.[143]​

La complejidad visual de las estructuras matemáticas, como las teselaciones y los poliedros, ha inspirado una gran variedad de obras de arte matemáticas. Stewart Coffin diseñó rompecabezas poliédricos en maderas raras y hermosas; George W. Hart trabajó en la teoría de poliedros y esculpió objetos inspirados en ellos; Magnus Wenninger realizó modelos "especialmente hermosos" de poliedros estrellados complejos.[144]​

Las perspectivas distorsionadas con efectos de anamorfosis se han explorado en el arte desde el siglo XVI, cuando Hans Holbein el Joven incorporó un cráneo severamente distorsionado en su pintura "Los embajadores" de 1533. Muchos artistas desde entonces, incluido Escher, han hecho uso de trucos anamórficos.[145]​

Las matemáticas propias de la topología han inspirado a varios artistas en los tiempos modernos. El escultor John Robinson (1935-2007) creó obras como Gordian Knot y Bands of Friendship, mostrando la teoría de nudos en bronce pulido.[8]​

Otros trabajos de Robinson exploran la topología de figuras toroidales. Su obra Genesis se basa en un nudo borromeo, un conjunto de tres aros entrelazados.[146]​ El escultor Helaman Ferguson creó complejas superficies y otros objetos topológicos.[147]​ Sus obras son representaciones visuales de objetos matemáticos; The Eightfold Way se basa en grupo lineal especial proyectivo PSL(2,7), un grupo finito de 168 elementos.[148]​[149]​ La escultora Bathsheba Grossman basó su trabajo en estructuras matemáticas de manera similar.[150]​[151]​

Un proyecto de investigación sobre artes liberales examina las conexiones entre las matemáticas y el arte a través de la banda de Möbius, flexágonos, origamis y fotografías panorámicas.[152]​

Los objetos matemáticos, incluidos el Atractor de Lorenz y el plano hiperbólico, se han creado utilizando el arte del tejido, incluido el crochet.[153]​[154]​[155]​ El tejedor estadounidense Ada Dietz escribió una monografía en 1949 titulada "Expresiones algebraicas en textiles tejidos a mano", que define patrones de tejido basados en la expansión de polinomios de múltiples variables.[156]​

El matemático J. C. P. Miller usó el autómata celular Rule 90 para diseñar tapices que representaban tanto árboles como patrones abstractos de triángulos.[157]​ Los "mathekniticians"[158]​ Pat Ashforth y Steve Plummer usaron versiones tejidas de objetos matemáticos como flexágonos para sus clases, aunque su esponja de Menger demostró ser demasiado compleja para tejerse y se confeccionó con lona plástica en su lugar.[159]​[160]​ Su proyecto "mathghans" (Afghanos en las Escuelas) introdujo el punto en el currículo británico de matemática y tecnología.[161]​[162]​

Ilustrando matemáticas[editar]
Tríptico Stefaneschi de Giotto (1320), ejemplo de recursión. A la derecha, detalle con el Cardenal Stefaneschi sujetando el tríptico completo
Fachada del Museo Magritte: el lienzo representa un escenario real envuelto por el propio lienzo
Autorretrato de M. C. Escher (1935) reflejado sobre una esfera de cristal

El modelado está lejos de ser la única manera posible de ilustrar conceptos matemáticos. El Tríptico Stefaneschi de Giotto (1320), ilustra la recursión en la forma de mise en abyme. El panel central del tríptico contiene en su parte inferior izquierda la figura arrodillada del cardenal Stefaneschi, sosteniendo el tríptico completo como ofrenda.[166]​ Las pinturas metafísicas de Giorgio de Chirico, como su "Gran Interior metafísico" de 1917, exploran la cuestión de los niveles de representación en el arte mediante la inclusión de pinturas dentro de sus pinturas.[167]​

El arte puede ejemplificar paradojas lógicas, como algunas pinturas del surrealista René Magritte, que se pueden leer como bromas de semiótica sobre la confusión entre niveles de significado. En La condition humaine (1933), Magritte representa un caballete (sobre el lienzo real), en el que aparece una vista a través de una ventana que está enmarcada por cortinas "reales" en la pintura. De manera similar, Print Gallery de Escher (1956), representa una ciudad distorsionada que contiene una galería en la que recursiónmente aparece la propia imagen, y así ad infinitum.[168]​ Magritte hizo uso de esferas y cuboides para distorsionar la realidad de forma diferente, pintándolas junto a distintas casas en su obra Aritmética mental de 1931 como si fueran bloques de construcción para niños, pero del tamaño de una casa.[169]​ Un artículo de The Guardian señalaba que la "imagen misteriosa de la ciudad de juguete" profetizaba la usurpación por parte del modernismo de las "tradicionales formas acogedoras", pero que también jugaba con la tendencia humana a buscar patrones en la naturaleza.[170]​

El cuadro de Salvador Dalí, La cola de golondrina (1983), fue parte de una serie inspirada en la teoría de las catástrofes de René Thom.[171]​ El pintor y escultor español Pablo Palazuelo (1916-2007) se centró en la investigación de la forma. Desarrolló un estilo que describió como la geometría de la vida y la geometría de toda la naturaleza, consistente en formas geométricas simples con patrones y colores detallados, en obras como Angular I y Automnes, Palazuelo se expresó mediante transformaciones geométricas.[8]​

El artista Adrian Gray ideó el equilibrio de rocas, jugando con las condiciones de fricción y el centro de masas para crear composiciones sorprendentes y aparentemente imposibles.[172]​

Los artistas, sin embargo, no necesariamente asumen literalmente las propiedades de la geometría como ciencia. Como Douglas Hofstadter escribió en su reflexión de 1980 sobre el pensamiento humano, Gödel, Escher, Bach: un Eterno y Grácil Bucle, a través de (entre otras cosas) las matemáticas del arte: "La diferencia entre un dibujo de Escher y la geometría no euclidiana es que en esta última, se pueden encontrar interpretaciones comprensibles para los términos indefinidos, lo que resulta en un sistema total comprensible, mientras que para el primero, el resultado final no se puede reconciliar con la propia concepción del mundo, sin importar cuánto se mire a las imágenes". Hofstadter discute la aparentemente paradójica litografía "Print Gallery" obra de M. C. Escher, que representa una ciudad costera que a su vez contiene una galería de arte que parece contener una pintura de la ciudad costera, con un "bucle extraño o jerarquía entramada" entre los distintos niveles de realidad de la imagen. El propio artista, observa Hofstadter, no se ve; su realidad y su relación con la litografía no son paradójicas.[173]​ El vacío central de la imagen también ha atraído el interés de los matemáticos Bart de Smit y Hendrik Lenstra, quienes proponen que podría contener una copia de sí misma, rotada y encogida mediante el efecto Droste; esta sería una ilustración más de la recursión más allá de lo señalado por Hofstadter.[174]​[175]​

Análisis de la historia del arte[editar]

El análisis algorítmico de imágenes de obras de arte, por ejemplo, utilizando fluorescencia de rayos X, puede revelar información sobre el arte. Tales técnicas pueden descubrir imágenes en capas de pintura cubiertas más tarde por un artista; ayudar a los historiadores del arte a visualizar una obra de arte antes de que se agriete o se desvanezca; ayudar a diferenciar una copia de un original, o distinguir el estilo de trazo de pincel de un maestro del de sus aprendices.[176]​[177]​

Max Ernst experimentó con curvas de Lissajous en la década de 1940

El estilo denominado dripping ("goteo") ideado por Jackson Pollock[178]​ posee una dimensión fractal definida;[179]​ entre los artistas que pueden haber influido en el chaos controlado de Pollock,[180]​ Max Ernst pintó curvas de Lissajous directamente haciendo balancearse un cubo de pintura agujereado colgado sobre un lienzo.[181]​

El científico informático Neil Dodgson investigó si las pinturas de rayas de Bridget Riley podían caracterizarse matemáticamente, concluyendo que si bien la distancia de separación podía "proporcionar cierta caracterización" y el concepto de entropía global funcionaba en algunas pinturas, la correlación obtenida no era concluyente, porque sus patrones eran irregulares. El análisis de la entropía local funcionó mejor, y se correlacionó bien con la descripción del crítico de arte Robert Kudielka.[182]​

La medida estética del matemático estadounidense George David Birkhoff, publicada en 1933, propone una métrica cuantitativa de la calidad estética de una obra de arte. No intenta medir las connotaciones de una obra, como el significado de una pintura, sino que se limita a los "elementos de orden" de una figura poligonal. Para ello, combina (como suma) cinco de estos parámetros: si existe un eje vertical de simetría; si hay equilibrio óptico; cuántas simetrías rotacionales tiene; cómo es el fondo de la figura; y si hay características insatisfactorias, como tener dos vértices demasiado juntos. Esta métrica, O, toma un valor entre −3 y 7. La segunda métrica, C, tiene en cuenta los elementos de la figura, que para un polígono es el número de diferentes líneas rectas que contienen al menos uno de sus lados. A continuación, define su medida estética de la belleza de un objeto como "O/C". Esto se puede interpretar como un equilibrio entre el placer de ver el objeto dado y la cantidad de esfuerzo necesario para asimilarlo. La propuesta de Birkhoff ha sido criticada de varias maneras, no solo por tratar de reducir la belleza a una fórmula, aunque siempre negó haberlo hecho.[183]​

Los estímulos a la investigación matemática[editar]

Véanse también: Geometría proyectiva y Matemáticas del origami.
Origami matemático: Muelle en Acción, por Jeff Beynon, construido con un único rectángulo de papel.[184]​
Origen remoto de la geometría proyectiva: diagrama de Alberti mostrando un círculo en perspectiva visto como una elipse. Della Pittura, 1435–6

El arte a veces ha estimulado el desarrollo de las matemáticas, como cuando la teoría de Brunelleschi sobre la arquitectura y la pintura supuso el inicio de un ciclo de investigación que condujo al trabajo de Brook Taylor y Johann Heinrich Lambert sobre los fundamentos matemáticos del dibujo en perspectiva,[185]​ y, en última instancia, a las matemáticas de la geometría proyectiva de Girard Desargues y Jean-Victor Poncelet.[186]​

El arte japonés de plegado de papel, el origami, ha sido revisado matemáticamente por Tomoko Fuse. Partiendo de piezas de papel congruentes, como cuadrados, analiza las operaciones necesarias para convertirlas en poliedros o teselas.[187]​ Esta técnica fue utilizada en 1893 por T. Sundara Rao en sus "Ejercicios geométricos de plegado de papel" para determinadas demostraciones geométricas.[188]​ Las matemáticas del origami han sido exploradas en el teorema de Maekawa,[189]​ el teorema de Kawasaki,[190]​ y en los axiomas de Huzita–Hatori.[191]​

Ilusiones ópticas y Op-art[editar]

Artículo principal: Op-art
Ilusión de la espiral de Fraser, nombrada así por Sir James Fraser, que la descubrió en 1908

Las ilusiones ópticas como la espiral de Fraser demuestran sorprendentemente las limitaciones en la percepción visual humana, creando lo que el historiador del arte Ernst Gombrich llamó un "truco desconcertante". Las líneas en blanco y negro que parecen formar espirales son de hecho concéntricas. El estilo de las pinturas y los gráficos del movimiento Op-art de mediados del siglo XX aprovechó tales efectos para crear la impresión de movimiento y patrones de vibración o destellos, propios del trabajo de artistas como Bridget Riley, Spyros Horemis,[192]​ y Victor Vasarely.[193]​

Geometría sagrada[editar]

Véanse también: Geometría sagrada y Música y matemáticas.

Una corriente del arte desde la antigua Grecia en adelante ve a Dios como el geómetra del mundo, y la geometría del mundo, por lo tanto, como sagrada. La creencia de que Dios creó el universo de acuerdo con un plan geométrico tiene orígenes antiguos. Plutarco atribuyó la creencia a Platón, escribiendo que "Platón dijo que Dios geometriza continuamente" (Convivialium disputationum, liber 8,2). Esta imagen ha influido en el pensamiento occidental desde entonces. El concepto platónico derivó a su vez de una noción de armonía pitagórica en la música, donde las notas estaban espaciadas en proporciones perfectas, correspondientes a las longitudes de las cuerdas de la lira; de hecho, los pitagóricos sostenían que todo estaba organizado por el Número. De la misma manera, en el pensamiento platónico, los sólidos platónicos (los cinco poliedros regulares convexos) dictan las proporciones encontradas en la naturaleza y en el arte.[194]​[195]​ Una ilustración de un manuscrito medieval puede referirse a un verso del Antiguo Testamento: "Cuando estableció los cielos, yo estaba allí: cuando estableció un compás sobre la faz de lo profundo" (Proverbios 8:27), que muestra a Dios dibujando el universo con un par de compases.[196]​

En 1596, el astrónomo y matemático Johannes Kepler modeló el universo como un conjunto de sólidos platónicos anidados, determinando los tamaños relativos de las órbitas de los planetas. Dos pinturas de William Blake, Ancient of Days[196]​ e Isaac Newton, intentan representar el contraste entre el mundo espiritual matemáticamente perfecto y el mundo físico imperfecto.[197]​ Salvador Dalí, por su parte, en su obra de 1954 Crucifixión, visualiza la cruz como un hipercubo, que representa la perspectiva divina con cuatro dimensiones en lugar de las tres habituales.[87]​ En otra de sus obras, La Última Cena (1955), Cristo y sus discípulos están representados en el interior de un gran dodecaedro.[198]​ gigante

Véase también[editar]

Referencias[editar]

  1. ↑ a b c Ziegler, Günter M. (3 de diciembre de 2014). «Dürer's polyhedron: 5 theories that explain Melencolia's crazy cube». The Guardian. Consultado el 27 de octubre de 2015. 
  2. ↑ a b Colombo, C.; Del Bimbo, A.; Pernici, F. (2005). «Metric 3D reconstruction and texture acquisition of surfaces of revolution from a single uncalibrated view». IEEE Transactions on Pattern Analysis and Machine Intelligence 27 (1): 99-114. PMID 15628272. doi:10.1109/TPAMI.2005.14. «10.1.1.58.8477». 
  3. ↑ a b Stewart, Andrew (November 1978). «Polykleitos of Argos," One Hundred Greek Sculptors: Their Careers and Extant Works». The Journal of Hellenic Studies 98: 122-131. JSTOR 630196. doi:10.2307/630196. 
  4. ↑ a b Tobin, Richard (October 1975). «The Canon of Polykleitos». American Journal of Archaeology 79 (4): 307-321. JSTOR 503064. doi:10.2307/503064. 
  5. ↑ Lawton, Arthur J. (2013). «Pattern, Tradition and Innovation in Vernacular Architecture». Past 36. Consultado el 25 de junio de 2015. «La figura base es un cuadrado de la longitud y el ancho de la falange distal del dedo meñique. Sus diagonales giradas hacia un lado transforman el cuadrado en un rectángulo de proporción 1:√2. En la Figura 5, esta figura rectangular marca el ancho y el largo de la falange medial adyacente. Se gira en diagonal la longitud de la falange medial para obtener la falange proximal y de manera similar desde allí hasta la muñeca, desde la muñeca hasta el codo y desde el codo hasta la parte superior del hombro. Cada nuevo paso avanza el punto de pivote de la diagonal.» 
  6. ↑ Raven, J. E. (1951). «Polyclitus and Pythagoreanism». Classical Quarterly 1 (3–4): 147-. doi:10.1017/s0009838800004122. 
  7. ↑ a b c O'Connor, J. J.; Robertson, E. F. (January 2003). «Mathematics and art – perspective». University of St Andrews. Consultado el 1 de septiembre de 2015. 
  8. ↑ a b c d Emmer, Michelle, ed. (2005). The Visual Mind II. MIT Press. ISBN 978-0-262-05048-7. 
  9. ↑ Vasari, Giorgio (1550). Lives of the Artists. Torrentino. p. Chapter on Brunelleschi. 
  10. ↑ Alberti, Leon Battista; Spencer, John R. (1956) [1435]. On Painting. Yale University Press. 
  11. ↑ Field, J. V. (1997). The Invention of Infinity: Mathematics and Art in the Renaissance. Oxford University Press. ISBN 978-0-19-852394-9. 
  12. ↑ Witcombe, Christopher L. C. E. «Art History Resources». Consultado el 5 de septiembre de 2015. 
  13. ↑ a b c d e Hart, George W.. «Polyhedra in Art». Consultado el 24 de junio de 2015. 
  14. ↑ Cunningham, Lawrence; Reich, John; Fichner-Rathus, Lois (1 de enero de 2014). Culture and Values: A Survey of the Western Humanities. Cengage Learning. p. 375. ISBN 978-1-285-44932-6. «que ilustran la fascinación de Uccello por la perspectiva. Los combatientes se amoldan a un campo de batalla lleno de lanzas rotas caídas sobre una cuadrícula virtual cercana y apuntan hacia un punto de fuga en algún lugar en la distancia.» 
  15. ↑ della Francesca, Piero (1942) [c. 1474]. G. Nicco Fasola, ed. De Prospectiva Pingendi. Florence. 
  16. ↑ della Francesca, Piero (1970) [Fifteenth century]. G. Arrighi, ed. Trattato d'Abaco. Pisa. 
  17. ↑ della Francesca, Piero (1916). G. Mancini, ed. L'opera "De corporibus regularibus" di Pietro Franceschi detto della Francesca usurpata da Fra Luca Pacioli. 
  18. ↑ Vasari, G. (1878). G. Milanesi, ed. Le Opere, volume 2. p. 490. 
  19. ↑ Zuffi, Stefano (1991). Piero della Francesca. L'Unità – Mondadori Arte. p. 53. 
  20. ↑ Heath, T.L. (1908). The Thirteen Books of Euclid's Elements. Cambridge University Press. p. 97. 
  21. ↑ Grendler, P. (1995). «What Piero Learned in School: Fifteenth-Century Vernacular Education». En M.A. Lavin, ed. Piero della Francesca and His Legacy (University Press of New England). pp. 161-176. 
  22. ↑ Alberti, Leon Battista; Grayson, Cecil (trans.) (1991). Kemp, Martin, ed. On Painting. Penguin Classics. 
  23. ↑ En el italiano de Piero della Francesca: "Una cosa tanto picholina quanto e possible ad ochio comprendere"
  24. ↑ Peterson, Mark. «The Geometry of Piero della Francesca». Archivado desde el original el 1 de julio de 2016. Consultado el 2 de abril de 2019. «En el Libro I, después de algunas construcciones elementales para presentar la idea de que el tamaño aparente de un objeto es en realidad su ángulo subtendido en el ojo, y refiriéndose a los Libros de los Elementos I y VI de Euclides, y a la Óptica de Euclides, se convierte, en la Proposición 13, en la representación de una plaza con su suelo tendido delante del espectador. ¿Qué debe dibujar realmente el artista? Después de esto, los objetos se construyen a partir de cuadrados (con diagonales, por ejemplo, para representar un piso de azulejos), y los objetos correspondientes se construyen en perspectiva; en el Libro II, los prismas se erigen sobre estos objetos planos, para representar casas, columnas, etc.; pero la base del método es el cuadrado original, del que sigue todo lo demás.» 
  25. ↑ Hockney, David (2006). Secret Knowledge: Rediscovering the Lost Techniques of the Old Masters. Thames and Hudson. ISBN 978-0-500-28638-8. 
  26. ↑ Van Riper, Frank. «Hockney's 'Lucid' Bomb At the Art Establishment». The Washington Post. Consultado el 4 de septiembre de 2015. 
  27. ↑ Marr, Andrew (7 de octubre de 2001). «What the eye didn't see». The Guardian. Consultado el 4 de septiembre de 2015. 
  28. ↑ Janson, Jonathan (25 de abril de 2003). «An Interview with Philip Steadman». Essential Vermeer. Consultado el 5 de septiembre de 2015. 
  29. ↑ Steadman, Philip (2002). Vermeer's Camera: Uncovering the Truth Behind the Masterpieces. Oxford. ISBN 978-0-19-280302-3. 
  30. ↑ Hart, George. «Luca Pacioli's Polyhedra». Consultado el 13 de agosto de 2009. 
  31. ↑ Morris, Roderick Conway (27 de enero de 2006). «Palmezzano's Renaissance:From shadows, painter emerges». New York Times. Consultado el 22 de julio de 2015. 
  32. ↑ Calter, Paul. «Geometry and Art Unit 1». Dartmouth College. Archivado desde el original el 21 de agosto de 2009. Consultado el 13 de agosto de 2009. 
  33. ↑ Brizio, Anna Maria (1980). Leonardo the Artist. McGraw-Hill. 
  34. ↑ Ladwein, Michael (2006). Leonardo Da Vinci, the Last Supper: A Cosmic Drama and an Act of Redemption. Temple Lodge Publishing. pp. 61-62. ISBN 978-1-902636-75-7. 
  35. ↑ Turner, Richard A. (1992). Inventing Leonardo. Alfred A. Knopf. 
  36. ↑ Wolchover, Natalie (31 de enero de 2012). «Did Leonardo da Vinci copy his famous 'Vitruvian Man'?». NBC News. Consultado el 27 de octubre de 2015. 
  37. ↑ Criminisi, A.; Kempz, M.; Kang, S. B. (2004). «Reflections of Reality in Jan van Eyck and Robert Campin». Historical Methods 37 (3): 109-121. doi:10.3200/hmts.37.3.109-122. 
  38. ↑ Cucker, Felix (2013). Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. Cambridge University Press. pp. 299-300, 306-307. ISBN 978-0-521-72876-8. 
  39. ↑ Cucker, Felix (2013). Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. Cambridge University Press. pp. 269–278. ISBN 978-0-521-72876-8. 
  40. ↑ Joyce, David E. (1996). «Euclid's Elements, Book II, Proposition 11». Clark University. Consultado el 24 de septiembre de 2015. 
  41. ↑ Seghers, M. J.; Longacre, J. J.; Destefano, G. A. (1964). «The Golden Proportion and Beauty». Plastic and Reconstructive Surgery 34 (4): 382-386. doi:10.1097/00006534-196410000-00007. 
  42. ↑ Mainzer, Klaus (1996). Symmetries of Nature: A Handbook for Philosophy of Nature and Science. Walter de Gruyter. p. 118. 
  43. ↑ «Mathematical properties in ancient theatres and amphitheatres». Archivado desde el original el 15 de julio de 2017. Consultado el 29 de enero de 2014. 
  44. ↑ «Architecture: Ellipse?». The-Colosseum.net. Archivado desde el original el 11 de diciembre de 2013. Consultado el 29 de enero de 2014. 
  45. ↑ a b c d Markowsky, George (January 1992). «Misconceptions about the Golden Ratio». The College Mathematics Journal 23 (1): 2-19. JSTOR 2686193. doi:10.2307/2686193. Archivado desde el original el 8 de abril de 2008. Consultado el 2 de abril de 2019. 
  46. ↑ Por ejemplo, se encuentran afirmaciones como: La relación del lado inclinado respecto a la mitad de la longitud de la base es de 1.619, a menos del 1% con respecto a la proporción áurea, lo que implica el uso del triángulo de Kepler (ángulo entre lados de 51°49'). Es más probable que las pirámides se hicieran con triángulos 3-4-5 (ángulo entre lados 53°8'), conocidos según se sabe por el Papiro de Ahmes; o con el triángulo con relación base/hipotenusa 1:4/π (ángulo de la cara 51°50').
  47. ↑ Taseos, Socrates G. (1990). Back in Time 3104 B.C. to the Great Pyramid. SOC Publishers. 
  48. ↑ Gazale, Midhat (1999). «Gnomon: From Pharaohs to Fractals». European Journal of Physics 20 (6) (Princeton University Press). p. 523. Bibcode:1999EJPh...20..523G. ISBN 978-0-691-00514-0. 
  49. ↑ Huntley, H.E. (1970). The Divine Proportion. Dover. 
  50. ↑ Hemenway, Priya (2005). Divine Proportion: Phi In Art, Nature, and Science. Sterling. p. 96. 
  51. ↑ Usvat, Liliana. «Mathematics of the Parthenon». Mathematics Magazine. Consultado el 24 de junio de 2015. 
  52. ↑ Boussora, Kenza; Mazouz, Said (Spring 2004). «The Use of the Golden Section in the Great Mosque of Kairouan». Nexus Network Journal 6 (1): 7-16. doi:10.1007/s00004-004-0002-y. Archivado desde el original el 4 de octubre de 2008. «La técnica geométrica de construcción de la sección áurea parece haber determinado las principales decisiones de la organización espacial. La sección áurea aparece repetidamente en algunas partes de las medidas del edificio. Se encuentra en la proporción general de la planta y en el dimensionamiento del espacio de oración, el patio y el minarete. La existencia de la sección áurea en algunas partes de la mezquita de Kairouan indica que los elementos diseñados y generados con este principio pueden haberse realizado en el mismo período.» 
  53. ↑ Brinkworth, Peter; Scott, Paul (2001). «The Place of Mathematics». Australian Mathematics Teacher 57 (3): 2. 
  54. ↑ Chanfón Olmos, Carlos (1991). Curso sobre Proporción. Procedimientos reguladores en construcción. Convenio de intercambio Unam–Uady. México – Mérica. 
  55. ↑ Livio, Mario (2002). «The Golden Ratio: The Story of Phi, The World's Most Astonishing Number». The Golden Ratio : The Story of Phi. Bibcode:2002grsp.book.....L. 
  56. ↑ Smith, Norman A. F. (2001). «Cathedral Studies: Engineering or History». Transactions of the Newcomen Society 73: 95-137. doi:10.1179/tns.2001.005. Archivado desde el original el 11 de diciembre de 2015. 
  57. ↑ McVeigh, Karen (28 de diciembre de 2009). «Why golden ratio pleases the eye: US academic says he knows art secret». The Guardian. Consultado el 27 de octubre de 2015. 
  58. ↑ Aarts, J.; Fokkink, R.; Kruijtzer, G. (2001). «Morphic numbers». Nieuw Arch. Wiskd. 5 2 (1): 56-58. 
  59. ↑ 'Plástico' hace referencia a la capacidad de tomar una forma tridimensional elegida.
  60. ↑ a b Padovan, Richard (2002). «Dom Hans Van Der Laan And The Plastic Number». En Williams, Kim; Francisco Rodrigues, Jose, eds. Nexus IV: Architecture and Mathematics: 181-193. 
  61. ↑ a b c d Salingaros, Nikos (November 1996). «The 'life' of a carpet: an application of the Alexander rules». 8th International Conference on Oriental Carpets. Archivado desde el original el 5 de marzo de 2016. Consultado el 2 de abril de 2019.  Reprinted in Eiland, M.; Pinner, M., eds. (1998). Oriental Carpet and Textile Studies V. Danville, CA: Conference on Oriental Carpets. 
  62. ↑ a b c Cucker, Felix (2013). Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. Cambridge University Press. pp. 89–102. ISBN 978-0-521-72876-8. 
  63. ↑ a b Lerner, Martin (1984). The flame and the lotus : Indian and Southeast Asian art from the Kronos collections (Exhibition Catalogue edición). Metropolitan Museum of Art. 
  64. ↑ a b Ellison, Elaine; Venters, Diana (1999). Mathematical Quilts: No Sewing Required. Key Curriculum. 
  65. ↑ a b Castera, Jean Marc; Peuriot, Francoise (1999). Arabesques. Decorative Art in Morocco. Art Creation Realisation. ISBN 978-2-86770-124-5. 
  66. ↑ Cucker, Felix (2013). Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. Cambridge University Press. pp. 103–106. ISBN 978-0-521-72876-8. 
  67. ↑ Dye, Daniel S. (1974). Chinese Lattice Designs. Dover. pp. 30–39. 
  68. ↑ belcastro, sarah-marie (2013). «Adventures in Mathematical Knitting». American Scientist 101 (2): 124. doi:10.1511/2013.101.124. Archivado desde el original el 4 de marzo de 2016. Consultado el 2 de abril de 2019. 
  69. ↑ Taimina, Daina (2009). Crocheting Adventures with Hyperbolic Planes. A K Peters. ISBN 978-1-56881-452-0. 
  70. ↑ Snook, Barbara. Florentine Embroidery. Scribner, Second edition 1967.
  71. ↑ Williams, Elsa S. Bargello: Florentine Canvas Work. Van Nostrand Reinhold, 1967.
  72. ↑ Grünbaum, Branko; Shephard, Geoffrey C. (May 1980). «Satins and Twills: An Introduction to the Geometry of Fabrics». Mathematics Magazine 53 (3): 139-161. Bibcode:1975MathM..48...12G. JSTOR 2690105. doi:10.2307/2690105. 
  73. ↑ a b Gamwell, Lynn (2015). Mathematics and Art: A Cultural History. Princeton University Press. p. 423. ISBN 978-0-691-16528-8. 
  74. ↑ Baker, Patricia L.; Smith, Hilary (2009). Iran (3 edición). Bradt Travel Guides. p. 107. ISBN 978-1-84162-289-7. 
  75. ↑ Irvine, Veronika; Ruskey, Frank (2014). «Developing a Mathematical Model for Bobbin Lace». Journal of Mathematics and the Arts 8 (3–4): 95-110. arXiv:1406.1532. doi:10.1080/17513472.2014.982938. 
  76. ↑ Lu, Peter J.; Steinhardt, Paul J. (2007). «Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture». Science 315 (5815): 1106-1110. Bibcode:2007Sci...315.1106L. PMID 17322056. doi:10.1126/science.1135491. 
  77. ↑ van den Hoeven, Saskia; van der Veen, Maartje. «Muqarnas-Mathematics in Islamic Arts». Archivado desde el original el 27 de septiembre de 2013. Consultado el 15 de enero de 2016. 
  78. ↑ Panofsky, E. (1955). The Life and Art of Albrecht Durer. Princeton. 
  79. ↑ Hart, George W. «Dürer's Polyhedra». Consultado el 13 de agosto de 2009. 
  80. ↑ Dürer, Albrecht (1528). Hierinn sind begriffen vier Bucher von menschlicher Proportion. Nurenberg. Consultado el 24 de junio de 2015. 
  81. ↑ Schreiber, P. (1999). «A New Hypothesis on Durer's Enigmatic Polyhedron in His Copper Engraving 'Melencolia I'». Historia Mathematica 26 (4): 369-377. doi:10.1006/hmat.1999.2245. 
  82. ↑ Dodgson, Campbell (1926). Albrecht Dürer. London: Medici Society. p. 94. 
  83. ↑ Schuster, Peter-Klaus (1991). Melencolia I: Dürers Denkbild. Berlin: Gebr. Mann Verlag. pp. 17-83. 
  84. ↑ Panofsky, Erwin; Klibansky, Raymond; Saxl, Fritz (1964). Saturn and melancholy. Basic Books. 
  85. ↑ Óleo sobre lienzo, 194.3 × 123.8 cm del Museo Metropolitano de Arte de Nueva York
  86. ↑ Rudy Rucker, The Fourth Dimension: Toward a Geometry of Higher Reality, Courier Corporation, 2014, ISBN 0486798194
  87. ↑ a b «Crucifixion (Corpus Hypercubus)». Metropolitan Museum of Art. Consultado el 5 de septiembre de 2015. 
  88. ↑ Lukman, Muhamad; Hariadi, Yun; Destiarmand, Achmad Haldani (2007). «Batik Fractal : Traditional Art to Modern Complexity». Proceeding Generative Art X, Milan, Italy. Consultado el 26 de septiembre de 2016. 
  89. ↑ Ouellette, Jennifer (November 2001). «Pollock's Fractals». Discover Magazine. Consultado el 26 de septiembre de 2016. 
  90. ↑ Galilei, Galileo (1623). The Assayer. , as translated in Drake, Stillman (1957). Discoveries and Opinions of Galileo. Doubleday. pp. 237–238. ISBN 978-0-385-09239-5. 
  91. ↑ Cucker, Felix (2013). Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. Cambridge University Press. p. 381. ISBN 978-0-521-72876-8. 
  92. ↑ Cucker, Felix (2013). Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. Cambridge University Press. p. 10. ISBN 978-0-521-72876-8. 
  93. ↑ King, Jerry P. (1992). The Art of Mathematics. Fawcett Columbine. pp. 8-9. ISBN 978-0-449-90835-8. 
  94. ↑ King, Jerry P. (1992). The Art of Mathematics. Fawcett Columbine. pp. 135-139. ISBN 978-0-449-90835-8. 
  95. ↑ Devlin, Keith (2000). «Do Mathematicians Have Different Brains?». The Math Gene: How Mathematical Thinking Evolved And Why Numbers Are Like Gossip. Basic Books. p. 140. ISBN 978-0-465-01619-8. 
  96. ↑ Wasilewska, Katarzyna (2012). «Mathematics in the World of Dance». Bridges. Consultado el 1 de septiembre de 2015. 
  97. ↑ a b Malkevitch, Joseph. «Mathematics and Art». American Mathematical Society. Consultado el 1 de septiembre de 2015. 
  98. ↑ Malkevitch, Joseph. «Mathematics and Art. 2. Mathematical tools for artists». American Mathematical Society. Consultado el 1 de septiembre de 2015. 
  99. ↑ «Math and Art: The Good, the Bad, and the Pretty». Mathematical Association of America. Consultado el 2 de septiembre de 2015. 
  100. ↑ Cohen, Louise (1 de julio de 2014). How to spin the colour wheel, by Turner, Malevich and more. Tate Gallery. Consultado el 4 de septiembre de 2015. 
  101. ↑ Kemp, Martin (1992). The Science of Art: Optical Themes in Western Art from Brunelleschi to Seurat. Yale University Press. ISBN 978-968-867-185-6. 
  102. ↑ Gage, John (1999). Color and Culture: Practice and Meaning from Antiquity to Abstraction. University of California Press. p. 207. ISBN 978-0-520-22225-0. 
  103. ↑ Malkevitch, Joseph. «Mathematics and Art. 3. Symmetry». American Mathematical Society. Consultado el 1 de septiembre de 2015. 
  104. ↑ Malkevitch, Joseph. «Mathematics and Art. 4. Mathematical artists and artist mathematicians». American Mathematical Society. Consultado el 1 de septiembre de 2015. 
  105. ↑ Wright, Richard (1988). «Some Issues in the Development of Computer Art as a Mathematical Art Form». Leonardo 1 (Electronic Art, supplemental issue): 103-110. JSTOR 1557919. doi:10.2307/1557919. 
  106. ↑ Kalajdzievski, Sasho (2008). Math and Art: An Introduction to Visual Mathematics. Chapman and Hall. ISBN 978-1-58488-913-7. 
  107. ↑ a b Beddard, Honor (26 de mayo de 2011). «Computer art at the V&A». Victoria and Albert Museum. Consultado el 22 de septiembre de 2015. 
  108. ↑ «Computer Does Drawings: Thousands of lines in each». The Guardian. 17 de septiembre de 1962.  in Beddard, 2015.
  109. ↑ O'Hanrahan, Elaine (2005). Drawing Machines: The machine produced drawings of Dr. D. P. Henry in relation to conceptual and technological developments in machine-generated art (UK 1960–1968). Unpublished MPhil. Thesis. John Moores University, Liverpool.  in Beddard, 2015.
  110. ↑ Bellos, Alex (24 de febrero de 2015). «Catch of the day: mathematician nets weird, complex fish». The Guardian. Consultado el 25 de septiembre de 2015. 
  111. ↑ «"A Bird in Flight (2016)," by Hamid Naderi Yeganeh». American Mathematical Society. 23 de marzo de 2016. Archivado desde el original el 29 de marzo de 2017. Consultado el 6 de abril de 2017. 
  112. ↑ Chung, Stephy (18 de septiembre de 2015). «Next da Vinci? Math genius using formulas to create fantastical works of art». CNN. 
  113. ↑ Levin, Golan (2013). «Generative Artists». CMUEMS. Archivado desde el original el 21 de septiembre de 2015. Consultado el 27 de octubre de 2015.  This includes a link to Hvidtfeldts Syntopia.
  114. ↑ Verostko, Roman. «The Algorists». Consultado el 27 de octubre de 2015. 
  115. ↑ a b Miller, Arthur I. (2001). Einstein, Picasso: Space, Time, and the Beauty That Causes Havoc. New York: Basic Books. p. 171. ISBN 978-0-465-01860-4. 
  116. ↑ Miller, Arthur I. (2012). Insights of Genius: Imagery and Creativity in Science and Art. Springer. ISBN 978-1-4612-2388-7. 
  117. ↑ Cucker, Felix (2013). Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. Cambridge University Press. pp. 315–317. ISBN 978-0-521-72876-8. 
  118. ↑ Henderson, Linda D. (1983). The Fourth Dimension and Non-Euclidean geometry in Modern Art. Princeton University Press. 
  119. ↑ Antliff, Mark; Leighten, Patricia Dee (2001). Cubism and Culture. Thames & Hudson. Archivado desde el original el 26 de julio de 2020. Consultado el 2 de abril de 2019.  (enlace roto)
  120. ↑ Everdell, William R. (1997). The First Moderns: Profiles in the Origins of Twentieth-Century Thought. University of Chicago Press. p. 312. ISBN 978-0-226-22480-0. 
  121. ↑ Green, Christopher (1987). Cubism and its Enemies, Modern Movements and Reaction in French Art, 1916–1928. Yale University Press. pp. 13–47. 
  122. ↑ Metzinger, Jean (October–November 1910). «Note sur la peinture». Pan: 60.  in Miller (2001). Einstein, Picasso. Basic Books. p. 167. 
  123. ↑ Metzinger, Jean (1972). Le cubisme était né. Éditions Présence. pp. 43-44.  in Ferry, Luc (1993). Homo Aestheticus: The Invention of Taste in the Democratic Age. Robert De Loaiza, trans. University of Chicago Press. p. 215. ISBN 978-0-226-24459-4. 
  124. ↑ «Man Ray–Human Equations A Journey from Mathematics to Shakespeare. February 7 – May 10, 2015». Phillips Collection. Consultado el 5 de septiembre de 2015. 
  125. ↑ Adcock, Craig (1987). «Duchamp's Eroticism: A Mathematical Analysis». Iowa Research Online 16 (1): 149-167. 
  126. ↑ Elder, R. Bruce (2013). DADA, Surrealism, and the Cinematic Effect. Wilfrid Laurier University Press. p. 602. ISBN 978-1-55458-641-7. 
  127. ↑ Tubbs, Robert (2014). Mathematics in Twentieth-Century Literature and Art: Content, Form, Meaning. JHU Press. p. 118. ISBN 978-1-4214-1402-7. 
  128. ↑ «Hiroshi Sugimoto Conceptual Forms and Mathematical Models February 7 – May 10, 2015». Phillips Collection. Consultado el 5 de septiembre de 2015. 
  129. ↑ Tubbs, Robert (2014). Mathematics in 20th-Century Literature and Art. Johns Hopkins. pp. 8-10. ISBN 978-1-4214-1380-8. 
  130. ↑ Keats, Jonathon (13 de febrero de 2015). «See How Man Ray Made Elliptic Paraboloids Erotic At This Phillips Collection Photography Exhibit». Forbes. Consultado el 10 de septiembre de 2015. 
  131. ↑ Gamwell, Lynn (2015). Mathematics and Art: A Cultural History. Princeton University Press. pp. 311-312. ISBN 978-0-691-16528-8. 
  132. ↑ Hedgecoe, John, ed. (1968). «Henry Moore: Text on His Sculpture». Henry Spencer Moore (Simon and Schuster). p. 105. 
  133. ↑ a b «De Stijl». Tate Glossary. The Tate. Consultado el 11 de septiembre de 2015. 
  134. ↑ Curl, James Stevens (2006). A Dictionary of Architecture and Landscape Architecture (Second edición). Oxford University Press. ISBN 978-0-19-860678-9. 
  135. ↑ Tubbs, Robert (2014). Mathematics in Twentieth-Century Literature and Art: Content, Form, Meaning. JHU Press. pp. 44-47. ISBN 978-1-4214-1402-7. 
  136. ↑ «Tour: M.C. Escher – Life and Work». NGA. Archivado desde el original el 3 de agosto de 2009. Consultado el 13 de agosto de 2009. 
  137. ↑ «MC Escher». Mathacademy.com. 1 de noviembre de 2007. Archivado desde el original el 11 de octubre de 2007. Consultado el 13 de agosto de 2009. 
  138. ↑ Penrose, L.S.; Penrose, R. (1958). «Impossible objects: A special type of visual illusion». British Journal of Psychology 49 (1): 31-33. PMID 13536303. doi:10.1111/j.2044-8295.1958.tb00634.x. 
  139. ↑ Kirousis, Lefteris M.; Papadimitriou, Christos H. (1985). «The complexity of recognizing polyhedral scenes». 26th Annual Symposium on Foundations of Computer Science (FOCS 1985). pp. 175-185. ISBN 978-0-8186-0644-1. doi:10.1109/sfcs.1985.59. «10.1.1.100.4844». 
  140. ↑ Cooper, Martin (2008). «Tractability of Drawing Interpretation». Line Drawing Interpretation. Springer-Verlag. pp. 217–230. ISBN 978-1-84800-229-6. doi:10.1007/978-1-84800-229-6_9. 
  141. ↑ Roberts, Siobhan (2006). «'Coxetering' with M.C. Escher». King of Infinite Space: Donald Coxeter, the Man Who Saved Geometry (Walker). p. Chapter 11. 
  142. ↑ Escher, M.C. (1988). The World of MC Escher. Random House. 
  143. ↑ Escher, M.C.; Vermeulen, M.W.; Ford, K. (1989). Escher on Escher: Exploring the Infinite. HN Abrams. 
  144. ↑ Malkevitch, Joseph. «Mathematics and Art. 5. Polyhedra, tilings, and dissections». American Mathematical Society. Consultado el 1 de septiembre de 2015. 
  145. ↑ Marcolli, Matilde (July 2016). The notion of Space in Mathematics through the lens of Modern Art. Century Books. pp. 23-26. 
  146. ↑ «John Robinson». Bradshaw Foundation. 2007. Consultado el 13 de agosto de 2009. 
  147. ↑ «Helaman Ferguson web site». Helasculpt.com. Archivado desde el original el 11 de abril de 2009. Consultado el 13 de agosto de 2009. 
  148. ↑ Thurston, William P. (1999). «The Eightfold Way: A Mathematical Sculpture by Helaman Ferguson». En Levy, Silvio, ed. Volume 35: The Eightfold Way: The Beauty of Klein's Quartic Curve (MSRI Publications). pp. 1-7. 
  149. ↑ «MAA book review of The Eightfold Way: The Beauty of Klein's Quartic Curve». Maa.org. 14 de noviembre de 1993. Archivado desde el original el 21 de diciembre de 2009. Consultado el 13 de agosto de 2009. 
  150. ↑ «The Math Geek Holiday Gift Guide». Scientific American. 23 de noviembre de 2014. Consultado el 7 de junio de 2015. 
  151. ↑ Hanna, Raven. «Gallery: Bathsheba Grossman». Symmetry Magazine. Consultado el 7 de junio de 2015. 
  152. ↑ Fleron, Julian F.; Ecke, Volker; von Renesse, Christine; Hotchkiss, Philip K. (January 2015). Art and Sculpture: Mathematical Inquiry in the Liberal Arts (2nd edición). Discovering the Art of Mathematics project. 
  153. ↑ Las imágenes y videos de la variedad de Lorenz realizadas por Hinke Osinga en ganchillo llegaron a los noticias de televisión internacionalmente, como se puede ver en el sitio web vinculado:Osinga, Hinke (2005). «Crocheting the Lorenz manifold». University of Auckland. Archivado desde el original el 10 de abril de 2015. Consultado el 12 de octubre de 2015. 
  154. ↑ Henderson, David; Taimina, Daina (2001). «Crocheting the hyperbolic plane». The Mathematical Intelligencer 23 (2): 17-28. doi:10.1007/BF03026623. .
  155. ↑ Osinga, Hinke M; Krauskopf, Bernd (2004). «Crocheting the Lorenz manifold». The Mathematical Intelligencer 26 (4): 25-37. doi:10.1007/BF02985416. Archivado desde el original el 19 de abril de 2013. Consultado el 2 de abril de 2019. «10.1.1.108.4594». 
  156. ↑ Dietz, Ada K. (1949), Algebraic Expressions in Handwoven Textiles, Louisville, Kentucky: The Little Loomhouse, archivado desde el original el 22 de febrero de 2016, consultado el 2 de abril de 2019 .
  157. ↑ Miller, J. C. P. (1970). «Periodic forests of stunted trees». Philosophical Transactions of the Royal Society. Series A, Mathematical and Physical Sciences 266 (1172): 63-111. Bibcode:1970RSPTA.266...63M. JSTOR 73779. doi:10.1098/rsta.1970.0003. 
  158. ↑ «Pat Ashforth & Steve Plummer – Mathekniticians». Woolly Thoughts. Consultado el 4 de octubre de 2015. 
  159. ↑ Ward, Mark (20 de agosto de 2012). «Knitting reinvented: Mathematics, feminism and metal». BBC News (BBC). Consultado el 23 de septiembre de 2015. 
  160. ↑ Ashforth, Pat; Plummer, Steve. «Menger Sponge». Woolly Thoughts: In Pursuit of Crafty Mathematics. Consultado el 23 de septiembre de 2015. 
  161. ↑ Ashforth, Pat; Plummer, Steve. «Afghans for Schools». Woolly Thoughts: Mathghans. Consultado el 23 de septiembre de 2015. 
  162. ↑ Mathghans with a Difference. Simply Knitting Magazine. 1 de julio de 2008. Archivado desde el original el 25 de septiembre de 2015. Consultado el 23 de septiembre de 2015. 
  163. ↑ Jouffret, Esprit (1903). Traité élémentaire de géométrie à quatre dimensions et introduction à la géométrie à n dimensions (en francés). Paris: Gauthier-Villars. OCLC 1445172. Consultado el 26 de septiembre de 2015. 
  164. ↑ Maurice Princet le dio una copia a Pablo Picasso, cuyos cuadernos de dibujo para Las señoritas de Avignon ilustran la influencia de Jouffret.
  165. ↑ Seckel, Hélène (1994). «Anthology of Early Commentary on Les Demoiselles d'Avignon». En William Rubin; Hélène Seckel; Judith Cousins, eds. Les Demoiselles d'Avignon. New York: Museum of Modern Art. p. 264. ISBN 978-0-87070-162-7. 
  166. ↑ «Giotto di Bondone and assistants: Stefaneschi triptych». The Vatican. Consultado el 16 de septiembre de 2015. 
  167. ↑ Gamwell, Lynn (2015). Mathematics and Art: A Cultural History. Princeton University Press. pp. 337-338. ISBN 978-0-691-16528-8. 
  168. ↑ Cooper, Jonathan (5 de septiembre de 2007). «Art and Mathematics». Consultado el 5 de septiembre de 2015. 
  169. ↑ Hofstadter, Douglas R. (1980). Gödel, Escher, Bach: An Eternal Golden Braid. Penguin. p. 627. ISBN 978-0-14-028920-6. 
  170. ↑ Hall, James (10 de junio de 2011). «René Magritte: The Pleasure Principle – exhibition». The Guardian. Consultado el 5 de septiembre de 2015. 
  171. ↑ King, Elliott (2004). Ades, Dawn, ed. Dali. Milan: Bompiani Arte. pp. 418-421. 
  172. ↑ «Stone balancing». Monthly Maths (29). July 2013. Archivado desde el original el 16 de abril de 2021. Consultado el 10 de junio de 2017. 
  173. ↑ Hofstadter, Douglas R. (1980). Gödel, Escher, Bach: An Eternal Golden Braid. Penguin. pp. 98-99, 690-717. ISBN 978-0-394-74502-2. 
  174. ↑ de Smit, B. (2003). «The Mathematical Structure of Escher's Print Gallery». Notices of the American Mathematical Society 50 (4): 446-451. 
  175. ↑ Lenstra, Hendrik; De Smit, Bart. «Applying mathematics to Escher's Print Gallery». Leiden University. Archivado desde el original el 14 de enero de 2018. Consultado el 10 de noviembre de 2015. 
  176. ↑ Stanek, Becca (16 de junio de 2014). «Van Gogh and the Algorithm: How Math Can Save Art». Time Magazine. Consultado el 4 de septiembre de 2015. 
  177. ↑ Sipics, Michelle (18 de mayo de 2009). «The Van Gogh Project: Art Meets Mathematics in Ongoing International Study». Society for Industrial and Applied Mathematics. Archivado desde el original el 7 de septiembre de 2015. Consultado el 4 de septiembre de 2015. 
  178. ↑ Emmerling, Leonhard (2003). Jackson Pollock, 1912–1956. p. 63. ISBN 978-3-8228-2132-9. 
  179. ↑ Taylor, Richard P.; Micolich, Adam P.; Jonas, David (June 1999). «Fractal analysis of Pollock's drip paintings». Nature 399 (6735): 422. Bibcode:1999Natur.399..422T. doi:10.1038/20833. Archivado desde el original el 16 de agosto de 2015. 
  180. ↑ Taylor, Richard; Micolich, Adam P.; Jonas, David (October 1999). «Fractal Expressionism: Can Science Be Used To Further Our Understanding Of Art?». Physics World 12 (10): 25-28. doi:10.1088/2058-7058/12/10/21. Archivado desde el original el 5 de agosto de 2012. Consultado el 2 de abril de 2019. «Pollock murió en 1956, antes de que se descubrieran la teoría del caos y los fractales. Por lo tanto, es muy poco probable que hubiera entendido conscientemente los fractales que estaba pintando. Sin embargo, su introducción de fractales fue deliberada. Por ejemplo, el color de la capa de anclaje se eligió para producir el contraste más nítido con el fondo del lienzo y esta capa también ocupa más espacio en el lienzo que las otras capas, lo que sugiere que Pollock quería que esta capa altamente fractal dominara visualmente la pintura. Además, una vez que se completaron las pinturas, recortó los lienzos para eliminar regiones cerca del borde donde la densidad del patrón era menos uniforme.» 
  181. ↑ King, M. (2002). «From Max Ernst to Ernst Mach: epistemology in art and science.». Consultado el 17 de septiembre de 2015. 
  182. ↑ Dodgson, N. A. (2012). «Mathematical characterisation of Bridget Riley's stripe paintings». Journal of Mathematics and the Arts 5 (2–3): 89-106. doi:10.1080/17513472.2012.679468. «over the course [of] the early 1980s, Riley's patterns moved from more regular to more random (as characterised by global entropy), without losing their rhythmic structure (as characterised by local entropy). This reflects Kudielka's description of her artistic development.» 
  183. ↑ Cucker, Felix (2013). Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. Cambridge University Press. pp. 116–120. ISBN 978-0-521-72876-8. 
  184. ↑ The World of Geometric Toys, Origami Spring, August, 2007.
  185. ↑ Treibergs, Andrejs (24 de julio de 2001). «The Geometry of Perspective Drawing on the Computer». University of Utah. Consultado el 5 de septiembre de 2015. 
  186. ↑ Gamwell, Lynn (2015). Mathematics and Art: A Cultural History. Princeton University Press. p. xviii. ISBN 978-0-691-16528-8. 
  187. ↑ Malkevitch, Joseph. «Mathematics and Art. 6. Origami». American Mathematical Society. Consultado el 1 de septiembre de 2015. 
  188. ↑ T. Sundara Rao (1893). Geometric Exercises in Paper Folding. Addison. 
  189. ↑ Justin, J. (June 1986). «Mathematics of Origami, part 9». British Origami: 28-30. .
  190. ↑ Alsina, Claudi; Nelsen, Roger (2010). Charming Proofs: A Journey Into Elegant Mathematics. Dolciani Mathematical Expositions 42. Mathematical Association of America. p. 57. ISBN 978-0-88385-348-1. 
  191. ↑ Alperin, Roger C.; Lang, Robert J. (2009). «One-, Two-, and Multi-Fold Origami Axioms». 4OSME. 
  192. ↑ Cucker, Felix (2013). Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. Cambridge University Press. pp. 163–166. ISBN 978-0-521-72876-8. 
  193. ↑ Gamwell, Lynn (2015). Mathematics and Art: A Cultural History. Princeton University Press. pp. 406-410. ISBN 978-0-691-16528-8. 
  194. ↑ Ghyka, Matila (2003). The Geometry of Art and Life. Dover. pp. ix–xi. ISBN 978-0-486-23542-4. 
  195. ↑ Lawlor, Robert (1982). Sacred Geometry: Philosophy and Practice. Thames & Hudson. ISBN 978-0-500-81030-9. 
  196. ↑ a b Calter, Paul (1998). «Celestial Themes in Art & Architecture». Dartmouth College. Archivado desde el original el 23 de junio de 2015. Consultado el 5 de septiembre de 2015. 
  197. ↑ «The Thought of a Thought – Edgar Allan Poe». MathPages. Consultado el 5 de septiembre de 2015. 
  198. ↑ Livio, Mario (November 2002). «The golden ratio and aesthetics». Consultado el 26 de junio de 2015. 

Enlaces externos[editar]

Obtenido de «https://es.wikipedia.org/w/index.php?title=Matemáticas_y_arte&oldid=158183718»