Geometría hiperbólica
La geometría hiperbólica o lobachevskiana es un modelo de geometría que satisface solo los cuatro primeros postulados de la geometría euclidiana. Aunque es similar en muchos aspectos y muchos de los teoremas de la geometría euclidiana siguen siendo válidos en geometría hiperbólica, no se satisface el quinto postulado de Euclides sobre las paralelas. Al igual que la geometría euclidiana y la geometría elíptica, la geometría hiperbólica es un modelo de curvatura constante:
- La geometría euclidiana satisface los cinco postulados de Euclides y tiene curvatura cero.
- La geometría hiperbólica satisface solo los cuatro primeros postulados de Euclides y tiene curvatura negativa.
- La geometría elíptica satisface solo los cuatro primeros postulados de Euclides y tiene curvatura positiva.
Historia[editar]
Desde la antigüedad se realizaron esfuerzos por deducir el quinto postulado de Euclides, referente a las paralelas, de los otros cuatro. Uno de los intentos más amplios y ambiciosos fue el de Giovanni Gerolamo Saccheri en el siglo XVIII quien, contradictoriamente creó lo que podríamos considerar modelo incipiente de geometría hiperbólica. Sin embargo, Saccheri creyó que no era consistente y no llegó a formalizar todos los aspectos de su trabajo. También Johann Heinrich Lambert encontró algunas fórmulas interesantes referentes a lo que hoy llamaríamos triángulos de la geometría hiperbólica, probando que la suma de los ángulos es siempre menor que 180° (o π radianes), la fórmula de Lambert establecía que para uno de estos triángulos se cumplía:
Donde:
- , es la suma de los ángulos del triángulo (expresada en radianes).
- , es el área total del triángulo.
- es una constante de proporcionalidad positiva relacionada con la curvatura constante del espacio hiperbólico en que se halla inmerso el triángulo.
Más adelante Carl Friedrich Gauss trabajó en un modelo similar pero no publicó sus resultados. En los años 1820 dos jóvenes matemáticos que trabajaban de modo independiente, János Bolyai y Nikolai Ivanovich Lobachevsky, publicaron sus modelos por los cuales establecían la posibilidad de un tipo de geometría alternativa, totalmente consistente, que es el que conocemos como geometría hiperbólica.
Introducción[editar]
Paralelas en la geometría hiperbólica[editar]


El axioma de Bolyai, equivalente al quinto postulado de Euclides sobre las rectas paralelas, que dice que «dada una recta r y un punto P externo a ella, hay una y solo una recta que pasa por P que no interseca a 'r''». Comúnmente, la recta que posee esta cualidad recibe el nombre de "paralela" a través de P.
En geometría hiperbólica, este postulado resulta falso puesto que siempre hay al menos dos rectas distintas que pasan por P y las cuales no intersecan a r. De hecho para la geometría hiperbólica es posible demostrar una interesante propiedad: hay dos clases de rectas que no intersecan a la recta r. Sea B un punto que pertenece a r tal que la recta PB es perpendicular a r. Considere la recta l que pasa por P, tal que l no interseca a r y el ángulo theta entre PB e l (en sentido contrario a las manecillas del reloj, desde PB) es lo más pequeño posible (es decir, cualquier ángulo más pequeño que theta, forzará a la recta a intersecar a r). Esta (l), es denominada recta hiperparalela (o simplemente, recta paralela) en la geometría hiperbólica.
En forma similar, la recta m que forma el mismo ángulo theta entre PB y ella misma, pero ahora en sentido de las manecillas del reloj desde PB, también será hiperparalela, pero no pueden haber otras. Todas las otras rectas que pasan por P y que no intersecan a r, forman ángulos más grandes que theta con PB y son llamadas rectas ultraparalelas (o rectas disjuntamente paralelas). Note que, al haber un número infinito de ángulos posibles entre θ y 90°, cada uno de estos determinará dos rectas que pasan por P y que son disjuntamente paralelas a r, tendremos entonces, un número infinito de rectas ultraparalelas. Por consiguiente, tenemos esta forma modificada del Postulado de las Rectas Paralelas: «En geometría hiperbólica, dada una recta r y un punto P exterior a r hay exactamente dos rectas que pasan por P, las cuales son hiperparalelas a r, e infinitas rectas que pasan por P y son ultraparalelas a r».
Las diferencias entre rectas hiperparalelas y ultraparaleas, también pueden ser vistas de la siguiente forma: la distancia entre rectas hiperparalelas tiende a cero mientras uno se aleja infinitamente de PB por la recta R. Sin embargo, la distancia entre rectas ultraparalelas no tiende a cero si uno se aleja infinitamente de PB por la recta r. El ángulo de paralelismo en la geometría euclidiana es una constante, es decir, cualquier longitud BP, determinará un ángulo de paralelismo igual a 90 grados. En la geometría hiperbólica, el ángulo de paralelismo varía con la que es llamada la función Π(p). Esta función, descrita por Nikolai Ivanovich Lobachevsky, produce un ángulo único de paralelismo para cada longitud dada BP. Mientras la longitud BP se haga más pequeña, el ángulo de paralelismo se acercará a 90°. Si la longitud BP incrementa sin límites, el ángulo de paralelismo se acercará a cero. Note que, debido a este hecho, mientras las distancias se hagan más pequeñas, el plano hiperbólico se comportará cada vez más como la Geometría Euclidiana. Por lo tanto, a pequeñas escalas, un observador en el plano hiperbólico tendrá dificultades para darse cuenta de que las distancias no se encuentran en un plano euclidiano.
En la geometría euclídea la suma de los ángulos de cualquier triángulo es siempre 180°. En la geometría hiperbólica esta suma es siempre menor de 180°, siendo la diferencia proporcional al área del triángulo.
Geometría hiperbólica y física[editar]
Podría muy bien suceder que la geometría hiperbólica fuera realmente verdadera en nuestro mundo a escala cosmológica. Sin embargo, la constante de proporcionalidad entre el déficit de ángulo para un triángulo y su área tendría que ser extraodinariamente pequeña en este caso, y la geometría euclídea sería una excelente aproximación a esta geometría para cualquier escala ordinaria.
Modelos euclídeos de la geometría hiperbólica[editar]
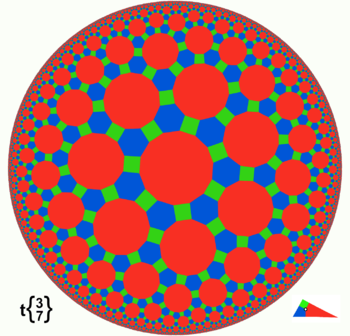
Existen cuatro modelos o representaciones "euclídeas" de la geometría hiperbólica: la representación de Klein, el modelo del Disco de Poincaré, el modelo del semiespacio de Poincaré y el modelo de Lorentz. Curiosamente los tres primeros modelos fueron propuestos y publicados originalmente por Eugenio Beltrami en 1868, sin embargo, alcanzaron notoriedad por el uso que tanto Felix Klein como Henri Poincaré hicieron de ellos, estos dos modelos son modelos de la geometría hiperbólica de dos dimensiones, y son generalizables a más dimensiones.
- La representación de Klein, también conocida como el modelo proyectivo del disco o modelo de Beltrami-Klein, usa el interior de un círculo como plano hiperbólico, y las cuerdas como líneas del círculo. Este modelo tiene como ventaja su simplicidad, pero como desventaja que los planos hiperbólicos están distorsionados.
- El modelo de Poincaré usa también el interior de un círculo plano, y en él las líneas rectas de la geometría hiperbólica vienen representadas por arcos de circunferencia que cortan el borde del círculo plano en ángulo recto.
Además este modelo es un modelo de curvatura constante negativa, que admite una representación como variedad riemanniana con un tensor métrico dado por:
Donde a es una constante relacionada con la curvatura K = -1/a2
Véase también[editar]
Referencias[editar]
Bibliografía[editar]
- A'Campo, Norbert y Papadopoulos, Athanase (2012), Notes on hyperbolic geometry, en: Strasbourg Master class on Geometry, pp. 1-182, IRMA Lectures in Mathematics and Theoretical Physics, Vol. 18, Zúrich: European Mathematical Society (EMS), 461 pp., SBN ISBN 978-3-03719-105-7, DOI 10.4171/105.
- Luis Santaló (1961), Geometrias no Euclidianas, EUDEBA.
- Robert M. Wald, General Relativity, Chicago University Press, ISBN 0-226-87033-2.
- Lee, J.M. Riemannian manifolds: an introduction to curvature. GTM 176. ISBN 0-387-98271-X





