Diferencia entre revisiones de «Matemáticas y arquitectura»

De Wikipedia, la enciclopedia libre
Ir a siguiente diferencia →
Contenido eliminado Contenido añadido
VisualWikitexto
Creación de «Matemáticas y arquitectura»
(Sin diferencias)

Revisión del 11:41 23 may 2021

Uno o varios wikipedistas están trabajando actualmente en este artículo o sección. Es posible que a causa de ello haya lagunas de contenido o deficiencias de formato.
Si quieres, puedes ayudar y editar, pero antes de realizar correcciones mayores contáctalos en sus páginas de discusión o en la del artículo para poder coordinar la redacción.
Uso de esta plantilla: {{En desarrollo|nombre de usuario|t={{sust:CURRENTTIMESTAMP}}}} o {{sust:En desarrollo}}

Introducción

"The Gherkin",[1]​ 30 St Mary Axe, Londres, completado en 2003, es un sólido de revolución diseñado paramétricamente
Kandariya Mahadeva Temple (c. 1030), Khajuraho, India, es un ejemplo de arquitectura religiosa con una estructura similar a un fractal, que tiene muchas partes que se asemejan al todo.[2]​

Matemáticas y arquitectura están relacionadas, ya que, como otros artistas, los arquitectos usan las matemáticas por varias razones. Además de las matemáticas necesarias al diseñar edificios, los arquitectos utilizan geometría: para definir la forma espacial de un edificio; desde el Pythagoreans del siglo VI aC en adelante, para crear formas consideradas armoniosas, y así diseñar los edificios y su entorno según principios matemáticos, estética y en ocasiones religiosos; para decorar edificios con objetos matemáticos como teselados; y para cumplir con los objetivos ambientales, como minimizar la velocidad del viento alrededor de las bases de los edificios altos.

En ancient Egypt, ancient Greece, India y Islamic world, los edificios que incluyen pyramids, templos, mezquitas, palacios y mausoleo se diseñaron con proporciones específicas por razones religiosas. En la arquitectura islámica, las formas geometric y geometric tiling patterns se utilizan para decorar edificios, tanto por dentro como por fuera. Algunos templos hindúes tienen una estructura similar a fractal donde las partes se asemejan al todo, transmitiendo un mensaje sobre el infinito en Cosmología hinduista. En Arquitectura china, los tulou de Fujian son estructuras defensivas comunales circulares. En el siglo XXI, la ornamentación matemática se está utilizando nuevamente para cubrir edificios públicos.

En Arquitectura del Renacimiento, simetría y la proporción fueron enfatizados deliberadamente por arquitectos como Leon Battista Alberti, Sebastiano Serlio y Andrea Palladio, influenciados por el Vitruvio de De architectura de antigua Roma y la aritmética de los pitagóricos de la antigua Grecia. A finales del siglo XIX, Vladímir Shújov en Rusia y Antoni Gaudí en Barcelona fueron pioneros en el uso de estructura hiperboloide; en el Templo Expiatorio de la Sagrada Familia, Gaudí también incorporó hyperbolic paraboloides, teselados, catenary arches, catenoides, helicoids y superficie regladas. En el siglo XX, estilos como arquitectura moderna y Deconstructivismo exploraron diferentes geometrías para lograr los efectos deseados. Los Superficie minimal se han explotado en cubiertas de techos en forma de carpa como en Aeropuerto Internacional de Denver, mientras que Richard Buckminster Fuller fue pionero en el uso de los fuertes estructura laminar conocidos como cúpula geodésica.

Campos conectados

In the Renacimiento, an arquitecto like Leon Battista Alberti was expected to be knowledgeable in many disciplines, including aritmética and geometría.

Los arquitectos Michael Ostwald y Kim Williams, considerando las relaciones entre arquitectura y matemáticas, señalan que los campos como comúnmente se entienden pueden parecer estar conectados débilmente, ya que la arquitectura es una profesión que se ocupa de la cuestión práctica de hacer edificios, mientras que las matemáticas son el study of number puro. y otros objetos abstractos. Pero, argumentan, los dos están fuertemente conectados, y lo han estado desde antiquity. En la antigua Roma, Vitruvio describió a un arquitecto como un hombre que conocía lo suficiente de una variedad de otras disciplinas, principalmente geometría, para permitirle supervisar a los artesanos expertos en todas las demás áreas necesarias, como albañiles y carpinteros. Lo mismo se aplicó en el Edad Media, donde los graduados aprendieron aritmética, geometría y estética junto con el programa básico de gramática, lógica y retórica (el artes liberales) en elegantes salones hechos por maestros constructores que habían guiado a muchos artesanos. Un maestro de obras en la cima de su profesión recibió el título de arquitecto o ingeniero. En el Renacimiento, el artes liberales de aritmética, geometría, música y astronomía se convirtió en un programa extra esperado de Polimatía como Leon Battista Alberti. De manera similar, en Inglaterra, Sir Christopher Wren, conocido hoy como arquitecto, fue en primer lugar un destacado astrónomo.[3]​

Williams y Ostwald, al revisar la interacción de las matemáticas y la arquitectura desde 1500 según el enfoque del sociólogo alemán Theodor Adorno, identifican tres tendencias entre los arquitectos, a saber: ser "revolucionario", introduciendo ideas completamente nuevas; "reaccionario", no introducir cambios; o revivalist , en realidad retrocediendo. Argumentan que los arquitectos han evitado buscar inspiración en las matemáticas en tiempos de avivamiento. Esto explicaría por qué en los períodos revivalistas, como el Gothic Revival en la Inglaterra del siglo XIX, la arquitectura tenía poca conexión con las matemáticas. Igualmente, señalan que en tiempos reaccionarios como el Manierismo italiano de alrededor de 1520 a 1580, o los movimientos Barroco y Palladianismo del siglo XVII, las matemáticas apenas se consultaban. En contraste, los movimientos revolucionarios de principios del siglo XX como Futurismo y Constructivism rechazaron activamente las viejas ideas, adoptando las matemáticas y conduciendo a la arquitectura Modernismo (movimiento filosófico y cultural). También hacia finales del siglo XX, los arquitectos se apoderaron rápidamente de la geometría fractal, al igual que teselado aperiódico, para proporcionar revestimientos interesantes y atractivos para los edificios.[4]​

Los arquitectos utilizan las matemáticas por varias razones, dejando de lado el uso necesario de las matemáticas en el engineering of buildings.[5]​ En primer lugar, utilizan la geometría porque define la forma espacial de un edificio.[6]​ En segundo lugar, utilizan las matemáticas para diseñar formas que son considered beautiful o armoniosas.[7]​ Desde la época de Pythagoreans con su filosofía religiosa del número, los arquitectos de[8]​ en ancient Greece, antigua Roma, Islamic world y Italian Renaissance han elegido los proportion del entorno construido - edificios y sus alrededores diseñados - de acuerdo con aspectos matemáticos, estéticos y, a veces, principios religiosos.[9]​[10]​[11]​[12]​ En tercer lugar, pueden utilizar objetos matemáticos como teselado para decorar edificios.[13]​[14]​ En cuarto lugar, pueden utilizar las matemáticas en forma de modelos informáticos para cuantificar el efecto de elementos ambientales, tale como las cargas generadas por el viento en la estructura de edificios altos.[1]​

Estética secular

Antigua Roma

Plan of a Greek house by Vitruvio

Vitruvio

Véanse también: Vitruvius, Vitruvian module y De architectura.
The interior of the Pantheon by Giovanni Pannini, 1758

El influyente arquitecto romano antiguo Vitruvio argumentó que el diseño de un edificio como un templo depende de dos cualidades, proporción y "simetría". La proporción asegura que cada parte de un edificio se relacione armoniosamente con todas las demás. Symmetria en el uso de Vitruvius significa algo más cercano al término inglés modularidad que mirror symmetry, ya que nuevamente se relaciona con el ensamblaje de partes (modulares) en todo el edificio. En su Basílica en Fano, usa proporciones de números enteros pequeños, especialmente los número triangular (1, ​​3, 6, 10, ...) para proporcionar la estructura en (Vitruvian) modules. [16]​ Por lo tanto, el ancho por largo de la Basílica es 1: 2; el pasillo que lo rodea es tan alto como ancho, 1: 1; las columnas tienen cinco pies de espesor y cincuenta pies de alto, 1:10.[9]​

Floor plan of the Pantheon

Vitruvio nombró tres cualidades requeridas de la arquitectura en su De architectura , c. 15 a.C .: firmeza, utilidad (o "mercancía" en el inglés del siglo XVI de Henry Wotton) y deleite. Estos se pueden utilizar como categorías para clasificar las formas en que se utilizan las matemáticas en la arquitectura. La firmeza abarca el uso de las matemáticas para garantizar que un edificio se mantenga en pie, de ahí las herramientas matemáticas utilizadas en el diseño y para apoyar la construcción, por ejemplo, para garantizar la estabilidad y el rendimiento del modelo. La utilidad se deriva en parte de la aplicación efectiva de las matemáticas, razonando y analizando las relaciones espaciales y de otro tipo en un diseño. El deleite es un atributo del edificio resultante, que resulta de la incorporación de relaciones matemáticas en el edificio; incluye cualidades estéticas, sensuales e intelectuales.[17]​

El Panteón

Artículo principal: Panteón de Agripa

El Pantheon en Roma ha sobrevivido intacto, ilustrando la estructura, proporción y decoración romanas clásicas. La estructura principal es una cúpula, el vértice se deja abierto como un óculo circular para dejar entrar la luz; tiene una columnata corta con frontón triangular. La altura del óculo y el diámetro del círculo interior son los mismos, 43,3 metros (142,1 pies), por lo que todo el interior encajaría exactamente dentro de un cubo, y el interior podría albergar una esfera del mismo diámetro.[18]​ Estas dimensiones tienen más sentido cuando se expresan en medidas y pesos en la Antigua Roma: El domo se extiende por 150 Roman feet[19]​); el óculo tiene 30 pies romanos de diámetro; la entrada tiene 40 pies romanos de altura.[20]​ El Pantheon sigue siendo la cúpula de hormigón no reforzado más grande del mundo.[21]​

Renacimiento

Véase también: Renaissance architecture
Facade of Basílica de Santa María Novella, Florencia, 1470. The frieze (with squares) and above is by Leon Battista Alberti.

El primer tratado renacentista de arquitectura fue el 1450 "De re aedificatoria" (Sobre el arte de la construcción) de Leon Battista Alberti; se convirtió en el primer libro impreso sobre arquitectura en 1485. Se basó en parte en la "De architectura" de Vitruvio y, a través de Nicomachus, en la aritmética pitagórica. Alberti comienza con un cubo y deriva proporciones de él. Así, la diagonal de una cara da la razón 1: √2, mientras que el diámetro de la esfera que circunscribe el cubo da 1: √3.[22]​[23]​ Alberti también documentó el descubrimiento de Filippo Brunelleschi por parte de perspectiva, desarrollado para permitir el diseño de edificios que se verían bellamente proporcionados cuando se veían desde una distancia conveniente.[12]​

Architectural perspective of a stage set by Sebastiano Serlio, 1569[24]​

El siguiente texto importante fue el "Regole generali d'architettura" (Reglas generales de arquitectura) de Sebastiano Serlio; el primer volumen apareció en Venecia en 1537; el volumen 1545 (libros 1 y 2) cubría la geometría y perspective. Dos de los métodos de Serlio para construir perspectivas estaban equivocados, pero esto no impidió que su trabajo fuera ampliamente utilizado.[25]​

Andrea Palladio's plan and elevation of the Villa Pisani

En 1570, Andrea Palladio publicó el influyente Los cuatro libros de la arquitectura (Los cuatro libros de arquitectura) en Venecia. Este libro ampliamente impreso fue en gran parte responsable de difundir las ideas del Renacimiento italiano por toda Europa, con la ayuda de proponentes como el diplomático inglés Henry Wotton con su 1624 "Los elementos de la arquitectura".[26]​ Las proporciones de cada habitación dentro de la villa se calcularon en proporciones matemáticas simples como 3: 4 y 4: 5, y las diferentes habitaciones dentro de la casa estaban interrelacionadas por estas proporciones. Los arquitectos anteriores habían utilizado estas fórmulas para equilibrar una sola fachada simétrica; sin embargo, los diseños de Palladio se relacionaban con toda la villa, generalmente cuadrada.[27]​ Palladio permitió un rango de proporciones en el Quattro libri , indicando:[28]​[29]​

There are seven types of room that are the most beautiful and well proportioned and turn out better: they can be made circular, though these are rare; or square; or their length will equal the diagonal of the square of the breadth; or a square and a third; or a square and a half; or a square and two-thirds; or two squares.[30]​

En 1615, Vincenzo Scamozzi publicó el tratado del Renacimiento tardío "L'idea dell'architettura universale" (La idea de una arquitectura universal).[31]​ Intentó relacionar el diseño de ciudades y edificios con las ideas de Vitruvio y los pitagóricos, y con las ideas más recientes de Palladio.[32]​

Siglo XIX

Hyperboloid lattice lighthouse by Vladímir Shújov, Ucrania, 1911

Los Estructura hiperboloide se utilizaron a partir de finales del siglo XIX por Vladímir Shújov para mástiles, faros y torres de refrigeración. Su llamativa forma es a la vez estéticamente interesante y fuerte, utilizando materiales estructurales de forma económica. Shukhov's first hyperboloidal tower se exhibió en Nizhni Nóvgorod en 1896.[33]​[34]​[35]​

Siglo XX

Véanse también: Arquitectura moderna y Arquitectura contemporánea.
De Stijl's sliding, intersecting planes: the Casa Rietveld Schröder, 1924

El movimiento de principios del siglo XX denominado arquitectura moderna, presagiado[37]​ por el constructivismo ruso,[36]​ usó geometría rectilínea Euclidean (también llamada Cartesian). En el movimiento De Stijl, lo horizontal y lo vertical fueron considerados como lo universal. La forma arquitectónica consiste en unir estas dos tendencias direccionales, utilizando planos de techo, planos de pared y balcones, que se deslizan o se cruzan, como en el Casa Rietveld Schröder de Gerrit Rietveld de 1924.[38]​

Raoul Heinrich Francé's poppy and pepperpot (biomimesis) image from Die Pflanze als Erfinder, 1920

Los arquitectos modernistas tenían libertad para hacer uso de curvas y planos. El Charles Holden de 1933 de Arnos station tiene una taquilla circular de ladrillo con un techo plano de hormigón.[39]​ En 1938, el pintor Escuela de la Bauhaus László Moholy-Nagy adoptó los siete elementos Raoul Heinrich Francé de biotechnical, a saber, el cristal, la esfera, el cono, el plano, la tira (cuboidal), la varilla (cilíndrica) y la espiral, como los supuestos bloques de construcción básicos de arquitectura inspirada en la naturaleza.[40]​[41]​

Le Corbusier propuso un antropometría scale de proporciones en arquitectura, el Modulor, basado en la supuesta altura de un hombre.[42]​ El Chapelle Notre-Dame du Haut de 1955 de Le Corbusier utiliza curvas de forma libre que no se pueden describir en fórmulas matemáticas. [45]​ Se dice que las formas evocan formas naturales como el proa de un barco o las manos en oración.[46]​ El diseño es solo a la escala más grande: no hay jerarquía de detalles a escalas más pequeñas y, por lo tanto, no hay dimensión fractal; lo mismo se aplica a otros edificios famosos del siglo XX, como el Ópera de Sídney, Aeropuerto Internacional de Denver y el Museo Guggenheim Bilbao.[43]​

Contemporary architecture, en opinión de los 90 arquitectos líderes que respondieron a un World Architecture Survey de 2010, es extremadamente diverso; el mejor fue juzgado como el Museo Guggenheim de Bilbao de Frank Gehry.[47]​

The superficie minimals of the fabric roof of Aeropuerto Internacional de Denver, completed in 1995, evoke Colorado's snow-capped mountains and the tipi tents of Native Americans.

El edificio de la terminal del Aeropuerto Internacional de Denver, terminado en 1995, tiene un fabric roof soportado como superficie minimal (es decir, su curvatura media es cero) por cables de acero. Evoca las montañas nevadas de Colorado y las tiendas de campaña tipi de Native American.[48]​[49]​

El arquitecto Richard Buckminster Fuller es famoso por diseñar estructura laminar fuertes conocidos como cúpula geodésica. El domo Biosphère de Montreal tiene una altura 61 metros (200,1 pies); su diámetro es 76 metros (249,3 pies).[50]​

Sydney Opera House tiene un techo espectacular que consta de elevadas bóvedas blancas, que recuerdan a las velas de los barcos; Para que sea posible construirlas con componentes estandarizados, las bóvedas están compuestas por secciones triangulares de conchas esféricas con el mismo radio. Estos tienen el uniforme curvatura requerido en todas las direcciones.[51]​

El movimiento Deconstructivismo de finales del siglo XX crea un desorden deliberado con lo que Nikos Salingaros en A Theory of Architecture llama formas aleatorias[52]​ de alta complejidad[53]​ mediante el uso de paredes no paralelas, rejillas superpuestas y superficies 2-D complejas, como en Walt Disney Concert Hall de Frank Gehry y el Museo Guggenheim de Bilbao. .[54]​[55]​ Hasta el siglo XX, los estudiantes de arquitectura estaban obligados a tener una base en matemáticas. Salingaros sostiene que primero Modernismo (movimiento filosófico y cultural) "excesivamente simplista y políticamente impulsado" y luego el deconstructivismo "anticientífico" han separado efectivamente la arquitectura de las matemáticas. Él cree que esta "inversión de los valores matemáticos" es dañina, ya que la "estética generalizada" de la arquitectura no matemática entrena a las personas "para rechazar la información matemática en el entorno construido"; argumenta que esto tiene efectos negativos en la sociedad.[43]​

Principios religiosos

Antiguo Egipto

Véase también: Golden ratio#Egyptian pyramids
Base:hypotenuse (b:a) ratios for pyramids like the Gran Pirámide de Guiza could be: 1:φ (Triángulo de Kepler), 3:5 (3:4:5 triangle), or 1:4/π

Los pirámide (arquitectura) de antiguo Egipto son tombs construidos con proporciones matemáticas, pero se debate cuáles fueron y si se utilizó Teorema de Pitágoras. La relación entre la altura inclinada y la mitad de la longitud de la base del Gran Pirámide de Guiza es inferior al 1% del número áureo.[56]​ Si este fuera el método de diseño, implicaría el uso de Kepler's triangle (ángulo de cara 51 ° 49 '),[56]​[57]​ pero según muchos historians of science, la proporción áurea no se conocía hasta el momento del Pitagóricos.[58]​ La Gran Pirámide también puede haberse basado en un triángulo con una relación de base a hipotenusa 1: 4 / π (ángulo de la cara 51 ° 50 ').[59]​

Las proporciones de algunas pirámides también pueden haberse basado en el 3:4:5 triangle (ángulo de la cara 53 ° 8 '), conocido por el Papiro de Ahmes (c. 1650-1550 BC); esto fue conjeturado por primera vez por el historiador Moritz Cantor en 1882.[60]​ Se sabe que los ángulos rectos se trazaron con precisión en el antiguo Egipto utilizando knotted cord para medir,[60]​ que Plutarco registró en Isis and Osiris (c. 100 d.C.) que los egipcios admiré el triángulo 3: 4: 5,[60]​ y que un pergamino de antes de 1700 BC demostraba fórmulas básicas de square.[61]​[62]​ El historiador Roger L. Cooke observa que "Es difícil imaginar a alguien interesado en tales condiciones sin conocer el teorema de Pitágoras", pero también señala que ningún texto egipcio anterior al 300 AC menciona en realidad el uso del teorema para encontrar la longitud de los lados de un triángulo, y que hay formas más sencillas de construir un ángulo recto. Cooke concluye que la conjetura de Cantor sigue siendo incierta; él supone que los antiguos egipcios probablemente conocían el teorema de Pitágoras, pero "no hay evidencia de que lo usaran para construir ángulos rectos".[60]​

Uno o varios wikipedistas están trabajando actualmente en este artículo o sección. Es posible que a causa de ello haya lagunas de contenido o deficiencias de formato.
Si quieres, puedes ayudar y editar, pero antes de realizar correcciones mayores contáctalos en sus páginas de discusión o en la del artículo para poder coordinar la redacción.
Uso de esta plantilla: {{En desarrollo|nombre de usuario|t={{sust:CURRENTTIMESTAMP}}}} o {{sust:En desarrollo}}

India antigua

Véanse también: Architecture of India y Vaastu Shastra.
Gopuram of the Hindú Virupaksha Temple has a fractal-like structure where the parts resemble the whole.

Vastu shastra, los antiguos cánones Indian de arquitectura y planificación urbana, emplea dibujos simétricos llamados mandalas. Se utilizan cálculos complejos para llegar a las dimensiones de un edificio y sus componentes. Los diseños están destinados a integrar la arquitectura con la naturaleza, las funciones relativas de varias partes de la estructura y creencias antiguas que utilizan patrones geométricos (yantra), simetría y alineaciones directional.[63]​[64]​ Sin embargo, los primeros constructores pueden haber encontrado proporciones matemáticas por accidente. El matemático Georges Ifrah señala que se pueden usar "trucos" simples con cuerdas y estacas para diseñar formas geométricas, como elipses y ángulos rectos.[12]​[65]​

Plan of Templo de Meenakshi Amman, Madurai, from 7th century onwards. The four gateways (numbered I-IV) are tall gopurams.

Las matemáticas de fractal se han utilizado para demostrar que la razón por la que los edificios existentes tienen un atractivo universal y son visualmente satisfactorios es porque brindan al espectador una sensación de escala a diferentes distancias de visión. Por ejemplo, en las puertas altas gopuram de los templos Hindú, como el Virupaksha Temple en Hampi construido en el siglo VII, y otros como el Kandariya Mahadev Temple en Khajuraho, las partes y el todo tienen el mismo carácter, con dimensión fractal en el rango de 1.7 a 1.8. . El grupo de torres más pequeñas ("shikhara", iluminado "montaña") alrededor de la torre central más alta que representa el santo Kailash, morada del Señor Shiva, representa la repetición interminable de universos en Cosmología hinduista.[2]​[66]​ El erudito en estudios religiosos William J. Jackson observó del patrón de torres agrupadas entre torres más pequeñas, agrupadas entre torres aún más pequeñas, que:

The ideal form gracefully artificed suggests the infinite rising levels of existence and consciousness, expanding sizes rising toward transcendence above, and at the same time housing the sacred deep within.[66]​[67]​

El Templo de Meenakshi Amman es un gran complejo con múltiples santuarios, con las calles de Madurai dispuestas concéntricamente a su alrededor de acuerdo con los shastras. Las cuatro puertas de entrada son torres altas (gopuram) con una estructura repetitiva de tipo fractal como en Hampi. Los recintos alrededor de cada santuario son rectangulares y están rodeados por altos muros de piedra.[68]​

Antigua Grecia

Véanse también: Greek architecture, Golden ratio, Pythagoreanism y Euclidean geometry.
The Partenón was designed using Pythagorean ratios.

Pitágoras (c. 569 - c. 475 a. C.) y sus seguidores, los pitagóricos, sostenían que "todas las cosas son números". Observaron las armonías producidas por notas con proporciones de frecuencia específicas de enteros pequeños y argumentaron que los edificios también deberían diseñarse con tales proporciones. La palabra griega symmetria denotaba originalmente la armonía de las formas arquitectónicas en proporciones precisas desde los detalles más pequeños de un edificio hasta su diseño completo.[12]​

El Partenón es 69,5 metros (228 pies) largo, 30,9 metros (101,4 pies) ancho y 13,7 metros (44,9 pies) alto hasta la cornisa. Esto da una relación de ancho a largo de 4: 9, y lo mismo para alto a ancho. Poniendo estos juntos da altura: ancho: largo de 16:36:81, o para el deleite[69]​ de los pitagóricos 42: 62: 92. Esto establece el módulo en 0.858 m. Un rectángulo de 4: 9 se puede construir como tres rectángulos contiguos con lados en una proporción de 3: 4. Cada medio rectángulo es entonces un conveniente triángulo rectángulo 3: 4: 5, que permite comprobar los ángulos y los lados con una cuerda debidamente anudada. El área interior (naos) tiene igualmente proporciones de 4: 9 (21,44 metros (70,3 pies) de ancho por 48,3 m de largo); la relación entre el diámetro de las columnas exteriores, 1,905 metros (6,3 pies), y el espaciado de sus centros, 4,293 metros (14,1 pies), también es de 4: 9.[12]​

Floor plan of the Parthenon

El Partenón es considerado por autores como John Julius Norwich "el templo dórico más perfecto jamás construido".[70]​ Sus elaborados refinamientos arquitectónicos incluyen "una correspondencia sutil entre la curvatura del estilobato, el ahusamiento de las paredes naos y la 'entasis' 'de las columnas".[70]​ Éntasis se refiere a la sutil disminución del diámetro de las columnas a medida que se elevan. El estilobato es la plataforma sobre la que se apoyan las columnas. Como en otros templos griegos clásicos,[71]​ la plataforma tiene una ligera curvatura parabólica hacia arriba para arrojar agua de lluvia y reforzar el edificio contra terremotos. Por lo tanto, podría suponerse que las columnas se inclinan hacia afuera, pero en realidad se inclinan ligeramente hacia adentro, de modo que si continúan, se encontrarían aproximadamente a un kilómetro y medio por encima del centro del edificio; dado que todos tienen la misma altura, la curvatura del borde estilóbico exterior se transmite al arquitrabe y al techo superior: "todos siguen la regla de estar construidos con curvas delicadas".[72]​

La proporción áurea se conoció en el 300 a.C., cuando Euclides describió el método de construcción geométrica.[73]​ Se ha argumentado que la proporción áurea se utilizó en el diseño del Partenón y otros edificios griegos antiguos, así como en esculturas, pinturas y jarrones.[74]​ Autores más recientes como Nikos Salingaros, sin embargo, dudan de todas estas afirmaciones.[75]​ Los experimentos del científico informático George Markowsky no lograron encontrar ninguna preferencia por el rectángulo dorado.[76]​

Arquitectura islámica

Véanse también: Islamic architecture y Golden ratio.
Mezquita de Selim, 1569–1575

El historiador del arte islámico Antonio Fernández-Puertas sugiere que la Alhambra, al igual que la Mezquita-catedral de Córdoba,[77]​ fue diseñada usando el pie andalusí o codo de aproximadamente 0,62 metros (2 pies). En el Patio de los Leones del palacio, las proporciones siguen una serie de surd. Un rectángulo de lados 1  y √2 tiene (por el teorema de Pitágoras) una diagonal de √3, que describe el triángulo rectángulo formado por lados del patio; esta serie continúa con √4 (dando una proporción de 1: 2), √5 y así sucesivamente. Los patrones decorativos tienen proporciones similares, √2 genera cuadrados dentro de círculos y estrellas de ocho puntas, √3 genera estrellas de seis puntas. No hay evidencia que respalde afirmaciones anteriores de que la proporción áurea se usó en la Alhambra.[10]​[78]​ El Patio de los Leones está delimitado por el Salón de las Dos Hermanas y el Salón de los Abencerrajes; Se puede dibujar un hexágono regular desde los centros de estos dos salones y las cuatro esquinas interiores del Patio de los Leones.[79]​

El Selimiye Mosque en Edirne, Turquía, fue construido por Sinan para proporcionar un espacio donde el mihrab pudiera verse desde cualquier lugar dentro del edificio. El gran espacio central está dispuesto, en consecuencia, como un octágono, formado por ocho pilares enormes y coronado por una cúpula circular de 31,25 metros (102,5 pies) de diámetro y 43 metros (141,1 pies) de altura. El octágono se forma en un cuadrado con cuatro semidomos, y externamente por cuatro minaretes excepcionalmente altos, 83 metros (272,3 pies) de altura. El plan del edificio es, por tanto, un círculo, dentro de un octágono, dentro de un cuadrado.[80]​

Arquitectura mogol

Artículos principales: Arquitectura mogola, Fatehpur Sikri y Origins and architecture of the Taj Mahal.
The Taj Mahal mausoleum with part of the complex's gardens at Agra

Arquitectura mogola, como se ve en la ciudad imperial abandonada de Fatehpur Sikri y el complejo Taj Mahal, tiene un orden matemático distintivo y una estética fuerte basada en la simetría y la armonía.[11]​[81]​

El Taj Mahal ejemplifica la arquitectura mogol, tanto representando paraíso[82]​ como mostrando el poder del Mughal Emperor Sha Jahan a través de su escala, simetría y decoración costosa. El mármol blanco mausoleo, decorado con pietra dura, la gran puerta ( Darwaza-i rauza ), otros edificios, los jardines y los caminos juntos forman un diseño jerárquico unificado. Los edificios incluyen un mezquita en piedra arenisca roja en el oeste, y un edificio casi idéntico, el Jawab o 'respuesta' en el este para mantener la simetría bilateral del complejo. El chahar bagh formal ('jardín cuádruple') se divide en cuatro partes, simbolizando los cuatro ríos del paraíso y ofreciendo vistas y reflejos del mausoleo. Estos se dividen a su vez en 16 parterres.[83]​

Site plan of the Taj Mahal complex. The great gate is at the right, the mausoleum in the centre, bracketed by the mosque (below) and the jawab. The plan includes squares and octógonos.

El complejo Taj Mahal se dispuso en una cuadrícula, subdividida en cuadrículas más pequeñas. Los historiadores de la arquitectura Koch y Barraud están de acuerdo con los relatos tradicionales que dan el ancho del complejo como 374 yardas mogol o gaz, siendo [84]​ el área principal tres cuadrados de 374 gaz. Estos se dividieron en áreas como el bazar y el caravasar en módulos de 17 gaz; el jardín y las terrazas están en módulos de 23 gaz y tienen 368 gaz de ancho (16 x 23). El mausoleo, la mezquita y la casa de huéspedes se distribuyen en una cuadrícula de 7 gaz. Koch y Barraud observan que si a un octágono, usado repetidamente en el complejo, se le dan lados de 7 units, entonces tiene un ancho de 17 unidades, [85]​, lo que puede ayudar a explicar la elección de proporciones en el complejo.[86]​

Arquitectura cristiana

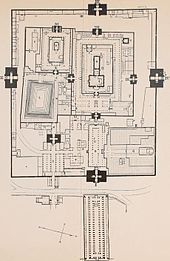
Véase también: Church architecture

El Christian patriarchal basílica de Santa Sofía en Bizancio (ahora Estambul), construido por primera vez en 537 (y reconstruido dos veces), fue durante mil años [87]​ la catedral más grande jamás construida. Inspiró muchos edificios posteriores, incluido Sultan Ahmed y otras mezquitas de la ciudad. El Arquitectura bizantina incluye una nave coronada por una cúpula circular y dos semicúpulas, todas del mismo diámetro (31 metros (101,7 pies)), con otras cinco semicúpulas más pequeñas que forman un ábside y cuatro esquinas redondeadas de un vasto interior rectangular.[88]​ Esto fue interpretado por arquitectos medievales como una representación de lo mundano abajo (la base cuadrada) y los cielos divinos arriba (la cúpula esférica elevada).[89]​ El emperador Justiniano I usó dos geómetras, Isidoro de Mileto y Antemio de Trales como arquitectos; Isidore compiló las obras de Arquímedes en geometría del espacio y fue influenciado por él.[12]​[90]​

Santa Sofía, Istanbul
a) Plan of gallery (upper half)
b) Plan of the ground floor (lower half)

La importancia del agua bautismo en el cristianismo se reflejó en la escala de la arquitectura baptisterio. El más antiguo, el Baptisterio de Letrán de Roma, construido en 440,[91]​ marcó la tendencia de los bautismos octogonales; el pila bautismal dentro de estos edificios era a menudo octogonal, aunque el baptistry, at Pisa más grande de Italia, construido entre 1152 y 1363, es circular, con una fuente octogonal. Es 54,86 metros (180 pies) alto, con un diámetro de 34,13 metros (112 pies) (una proporción de 8: 5).[92]​ Ambrosio de Milán escribió que las pilas y los bautismos eran octogonales "porque al octavo día, [94]​ al levantarse, Cristo afloja la esclavitud de la muerte y recibe a los muertos de sus tumbas".[93]​[95]​ Agustín de Hipona describió de manera similar el octavo día como "eterno ... santificado por el resurrección de Cristo".[95]​[96]​ El Baptistry of Saint John, Florence octogonal, construido entre 1059 y 1128, es uno de los edificios más antiguos de esa ciudad, y uno de los últimos en la tradición directa de la antigüedad clásica; fue extremadamente influyente en el Renacimiento florentino posterior, ya que los principales arquitectos, incluidos Francesco Talenti, Alberti y Brunelleschi, lo utilizaron como modelo de arquitectura clásica.[97]​

El número cinco se usa "exuberantemente"[98]​ en el 1721 Iglesia de peregrinación de San Juan Nepomuceno en Zelená hora, cerca de Žďár nad Sázavou en la República Checa, diseñado por Jan Blažej Santini Aichel. La nave es circular, rodeada por cinco pares de columnas y cinco cúpulas ovaladas que se alternan con ábsides ojivales. Además, la iglesia tiene cinco puertas, cinco capillas, cinco altares y cinco estrellas; una leyenda afirma que cuando Juan Nepomuceno fue martirizado, cinco estrellas aparecieron sobre su cabeza.[98]​[99]​ El f



La arquitectura de cinco pliegues también puede simbolizar el cinco llagas de Jesucristo y las cinco letras de "Tacui" (en latín: "Guardé silencio" [sobre los secretos del confesonario]).[100]​

Antoni Gaudí utilizó una amplia variedad de estructuras geométricas, algunas de las cuales eran superficies mínimas, en Templo Expiatorio de la Sagrada Familia, Barcelona, que comenzó en 1882 (y no se completó en 2015). Estos incluyen paraboloide hiperbólicos y hyperboloids of revolution, teselaciones[101]​, catenary arch, catenoide, helicoid y superficie reglada. Esta variada mezcla de geometrías se combina creativamente de diferentes formas en la iglesia. Por ejemplo, en la Fachada de la Pasión de la Sagrada Familia, Gaudí ensambló "ramas" de piedra en forma de paraboloides hiperbólicos, que se superponen en sus puntas (directrices) sin, por tanto, encontrarse en un punto. En contraste, en la columnata hay superficies paraboloidales hiperbólicas que se unen suavemente a otras estructuras para formar superficies ilimitadas. Además, Gaudí explota natural patterns, en sí mismo matemático, con columna (arquitectura) derivados de las formas de árbol, y dintel hechos de basalto sin modificar naturalmente agrietado (por enfriamiento de roca fundida) en hexagonal columns.[102]​[103]​[104]​

El 1971 Cathedral of Saint Mary of the Assumption, San Francisco tiene un saddle roof compuesto por ocho segmentos de paraboloides hiperbólicos, dispuestos de manera que la sección transversal horizontal inferior del techo es un cuadrado y la sección transversal superior es un Cruz cristiana. El edificio es un 77,7 metros (254,9 pies) cuadrado en un lado y 57,9 metros (190 pies) alto.[105]​ El Catedral de Brasilia de 1970 de Oscar Niemeyer hace un uso diferente de una estructura hiperboloide; está construido con 16 vigas de hormigón idénticas, cada una con un peso de 90 toneladas, [106]​ dispuestas en un círculo para formar un hiperboloide de revolución, las vigas blancas crean una forma como manos rezando al cielo. Solo la cúpula es visible desde el exterior: la mayor parte del edificio está bajo tierra.[107]​[108]​[109]​[110]​

Varios churches in Scandinavia are circular medievales, incluidos cuatro en la isla danesa de Bornholm. Uno de los más antiguos, Østerlars Church de c. 1160, tiene una nave circular alrededor de una enorme columna circular de piedra, perforada con arcos y decorada con un fresco. La estructura circular tiene tres pisos y aparentemente fue fortificada, habiendo servido el suelo superior de defensa.[111]​ [112]​

Decoración matemática

Decoración arquitectónica islámica

Artículo principal: Patrones geométricos islámicos

Los edificios islámicos a menudo están decorados con geometric patterns, que generalmente utilizan varios teselado matemáticos, formados por baldosas de cerámica (girih, zellige) que pueden ser lisas o decoradas con rayas.[12]​ Las simetrías, como las estrellas con seis, ocho o múltiplos de ocho puntos, se utilizan en patrones islámicos. Algunos de estos se basan en el motivo del sello de 'Khatem Sulemani' o de Salomón, que es una estrella de ocho puntas formada por dos cuadrados, uno girado a 45 grados del otro en el mismo centro.[113]​ Los patrones islámicos explotan muchos de los 17 posibles grupo del papel pintado; Ya en 1944, Edith Müller demostró que la Alhambra hacía uso de 11 grupos de papel tapiz en sus decoraciones, mientras que en 1986 Branko Grünbaum afirmó haber encontrado 13 grupos de papel tapiz en la Alhambra, afirmando de manera controvertida que los cuatro grupos restantes no se encuentran en ninguna parte de la ornamentación islámica. .[113]​

Decoración arquitectónica moderna

Véanse también: Ornament (art) y Contemporary architecture.

Hacia finales del siglo XX, los arquitectos recurrieron a nuevas construcciones matemáticas como la geometría fractal y el mosaico aperiódico para proporcionar revestimientos interesantes y atractivos para los edificios.[4]​ En 1913, el arquitecto modernista Adolf Loos había declarado que "El ornamento es un crimen", influyendo[114]​ en el pensamiento arquitectónico durante el resto del siglo XX. En el siglo XXI, los arquitectos están comenzando nuevamente a explorar el uso de ornament. La ornamentación del siglo XXI es extremadamente diversa. Harpa (Reikiavik) 2011 de Henning Larsen, Reykjavik tiene lo que parece una pared de roca de cristal hecha de grandes bloques de vidrio.[114]​ Foreign Office Architects 2010 Ravensbourne College, Londres está teselado decorativamente con 28.000 baldosas de aluminio anodizado en rojo, blanco y marrón, ventanas circulares entrelazadas de diferentes tamaños. La teselación utiliza tres tipos de mosaicos, un triángulo equilátero y dos pentágonos irregulares.[115]​[116]​[117]​ Biblioteca Umimirai de Kanazawa de Kazumi Kudo crea una rejilla decorativa hecha de pequeños bloques circulares de vidrio colocados en paredes de concreto liso.[114]​

Defensa

Europa

Véase también: Star fort

La arquitectura de fortificación evolucionó de medieval fortresses, que tenía altos muros de mampostería, a traza italiana bajos y simétricos capaces de resistir el bombardeo de artillería entre mediados del siglo XV y XIX. La geometría de las formas de las estrellas fue dictada por la necesidad de evitar zonas muertas donde la infantería atacante pudiera protegerse del fuego defensivo; los lados de los puntos salientes estaban en ángulo para permitir que dicho fuego barriera el suelo y proporcionara fuego cruzado (desde ambos lados) más allá de cada punto saliente. Los arquitectos conocidos que diseñaron tales defensas incluyen Miguel Ángel, Baldassarre Peruzzi, Vincenzo Scamozzi y Vauban.[118]​[119]​

El historiador arquitectónico Sigfried Giedion argumentó que la fortificación en forma de estrella tuvo una influencia formativa en el patrón del Renacimiento ideal city: "El Renacimiento fue hipnotizado por un tipo de ciudad que durante un siglo y medio, desde Filarete hasta Scamozzi, quedó impresionado en todos los utópicos. esquemas: este es el


ciudad en forma de estrella ".[120]​

China

A tulou in Yongding, Fujian

En Arquitectura china, los tulou de Fujian son estructuras defensivas comunales circulares con paredes principalmente en blanco y una sola puerta de madera chapada en hierro, algunas que datan del siglo XVI. Los muros se rematan con tejados que se inclinan suavemente tanto hacia el exterior como hacia el interior, formando un anillo. El centro del círculo es un patio adoquinado abierto, a menudo con un pozo, rodeado de galerías de madera de hasta cinco pisos de altura.[121]​

Objetivos medioambientales

Yakhchal in Yazd, Iran

Los arquitectos también pueden seleccionar la forma de un edificio para cumplir con los objetivos ambientales.[98]​ Por ejemplo, Foster and Partners '30 St Mary Axe, Londres, conocido como "The Gherkin" por su forma similar a cucumis sativus, es un sólido de revolución diseñado con parametric modelling. Su geometría no se eligió por razones puramente estéticas, sino para minimizar las corrientes de aire en remolino en su base. A pesar de la superficie aparentemente curva del edificio, todos los paneles de vidrio que forman su piel son planos, excepto la lente en la parte superior. La mayoría de los paneles son cuadrilátero, ya que se pueden cortar de vidrio rectangular con menos desperdicio que los paneles triangulares.[1]​

El tradicional yakhchal (pozo de hielo) de Persia funcionó como un refrigeración por evaporación. Sobre el suelo, la estructura tenía forma de cúpula, pero tenía un espacio de almacenamiento subterráneo para el hielo y, a veces, también para la comida. El espacio subterráneo y la construcción gruesa resistente al calor aislaron el espacio de almacenamiento durante todo el año. El espacio interno a menudo se enfría aún más con captador de viento. El hielo estuvo disponible en verano para hacer el postre helado faloodeh.[122]​en contra

Ver también

Notas

  1. ↑ a b c Freiberger, Marianne (1 March 2007). «Perfect buildings: the maths of modern architecture». Plus magazine. Consultado el 5 October 2015. 
  2. ↑ a b Rian, Iasef Md; Park, Jin-Ho; Ahn, Hyung Uk; Chang, Dongkuk (2007). «Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho». Building and Environment 42 (12): 4093-4107. doi:10.1016/j.buildenv.2007.01.028. 
  3. ↑ Williams, Kim; Ostwald, Michael J., eds. (2015). Architecture and Mathematics from Antiquity to the Future: Volume I: from Antiquity to the 1500s. Birkhäuser. pp. chapter 1. 1-24. ISBN 978-3-319-00136-4. 
  4. ↑ a b Williams, Kim; Ostwald, Michael J., eds. (2015). Architecture and Mathematics from Antiquity to the Future: Volume II: The 1500s to the Future. Birkhäuser. pp. chapter 48. 1-24. ISBN 978-3-319-00142-5. 
  5. ↑ «Architectural Engineering Overview». Sloan Career Cornerstone Center. Archivado desde el original el 14 July 2015. Consultado el 11 October 2015.  Parámetro desconocido |url-status= ignorado (ayuda)
  6. ↑ Leyton, Michael (2001). A Generative Theory of Shape. Springer. ISBN 978-3-540-42717-9. 
  7. ↑ Stakhov, Alexey; Olsen, Olsen (2009). The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science. World Scientific. ISBN 978-981-277-582-5. 
  8. ↑ Smith, William (1870). Dictionary of Greek and Roman Biography and Mythology. Little, Brown. p. 620. 
  9. ↑ a b Vitruvius (2009). On Architecture. Penguin Books. pp. 8-9. ISBN 978-0-14-193195-1. 
  10. ↑ a b Tennant, Raymond (July 2003). «International Joint Conference of ISAMA, the International Society of the Arts, Mathematics, and Architecture, and BRIDGES. Mathematical Connections in Art Music, and Science, University of Granada, Spain, July, 2003. Islamic Constructions: The Geometry Needed by Craftsmen.». International Joint Conference of ISAMA, the International Society of the Arts, Mathematics, and Architecture, and BRIDGES, Mathematical Connections in Art Music, and Science. 
  11. ↑ a b Rai, Jaswant (1993). «Mathematics and Aesthetics in Islamic Architecture: Reference to Fatehpur Sikri». Journal of King Saud University, Architecture & Planning 5 (1): 19-48. Uso incorrecto de la plantilla enlace roto (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
  12. ↑ a b c d e f g O'Connor, J. J.; Robertson, E. F. (February 2002). «Mathematics and Architecture». University of St Andrews. Consultado el 4 October 2015. 
  13. ↑ van den Hoeven, Saskia; van der Veen, Maartje (2010). «Muqarnas: Mathematics in Islamic Arts». Utrecht University. Archivado desde el original el 4 March 2016. Consultado el 30 September 2015.  Parámetro desconocido |url-status= ignorado (ayuda)
  14. ↑ Cucker, Felipe (2013). Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. Cambridge University Press. pp. 103-106. ISBN 978-0-521-72876-8. 
  15. ↑ Vitruvius. «VITRUVIUS, BOOK IV, CHAPTER 3 On the Doric order». Vitruvius.be. Consultado el 6 October 2015. 
  16. ↑ In Book 4, chapter 3 of De architectura, he discusses modules directly.[15]​
  17. ↑ Williams, Kim; Ostwald, Michael J. (9 February 2015). Architecture and Mathematics from Antiquity to the Future: Volume I: Antiquity to the 1500s. Birkhäuser. pp. 42, 48. ISBN 978-3-319-00137-1. 
  18. ↑ Roth, Leland M. (1992). Understanding Architecture: Its Elements, History, And Meaning. Boulder: Westview Press. p. 36. ISBN 0-06-438493-4. 
  19. ↑ A Medidas y pesos en la Antigua Roma was about 0,296 metros (1 pies).
  20. ↑ Claridge, Amanda (1998). Rome. Oxford Archaeological Guides. Oxford Oxfordshire: Oxford University Press. pp. 204–5. ISBN 0-19-288003-9. 
  21. ↑ Lancaster, Lynne C. (2005). Concrete Vaulted Construction in Imperial Rome: Innovations in Context. Cambridge: Cambridge University Press. pp. 44–46. ISBN 0-521-84202-6. 
  22. ↑ March, Lionel (1996). «Renaissance mathematics and architectural proportion in Alberti's De re aedificatoria». Architectural Research Quarterly 2 (1): 54-65. doi:10.1017/S135913550000110X. 
  23. ↑ «Sphere circumscribing a cube». Mathalino.com Engineering Math Review. Consultado el 4 October 2015. 
  24. ↑ Typ 525.69.781, Houghton Library, Harvard University
  25. ↑ Andersen, Kirsti (2008). The Geometry of an Art: The History of the Mathematical Theory of Perspective from Alberti to Monge. Springer. pp. 117–121. ISBN 978-0-387-48946-9.  Parámetro desconocido |title-link= ignorado (ayuda)
  26. ↑ Ruhl, Carsten (7 April 2011). «Palladianism: From the Italian Villa to International Architecture». European History Online. Consultado el 3 October 2015. 
  27. ↑ Copplestone, Trewin (1963). World Architecture. Hamlyn. p. 251. (requiere registro). 
  28. ↑ Wassell, Stephen R. «The Mathematics Of Palladio's Villas: Workshop '98». Nexus Network Journal. Consultado el 3 October 2015. 
  29. ↑ Palladio, Andrea; Tavernor, Robert; Schofield, Richard (trans.) (1997). I quattro libri dell'architettura. MIT Press. p. book I, chapter xxi, page 57.  Parámetro desconocido |orig-year= ignorado (ayuda)
  30. ↑ In modern algebraic notation, these ratios are respectively 1:1, √2:1, 4:3, 3:2, 5:3, 2:1.
  31. ↑ Scamozzi, Vincenzo; Vroom, W. H. M. (trans.) (2003). The Idea of a Universal Architecture. Architectura & Natura.  Parámetro desconocido |orig-year= ignorado (ayuda)
  32. ↑ Borys, Ann Marie (28 March 2014). Vincenzo Scamozzi and the Chorography of Early Modern Architecture. Ashgate Publishing. pp. 140-148 and passim. ISBN 978-1-4094-5580-6. 
  33. ↑ Beckh, Matthias (2015). Hyperbolic Structures: Shukhov's Lattice Towers – Forerunners of Modern Lightweight Construction. John Wiley & Sons. pp. 75 and passim. ISBN 978-1-118-93268-1. 
  34. ↑ «The Nijni-Novgorod exhibition: Water tower, room under construction, springing of 91 feet span». The Engineer: 292-294. 19 March 1897. 
  35. ↑ Graefe, Rainer (1990). Vladimir G. Suchov 1853–1939. Die Kunst der sparsamen Konstruktion. Deutsche Verlags-Anstalt. pp. 110–114. ISBN 3-421-02984-9. 
  36. ↑ a b Hatherley, Owen (4 November 2011). «The Constructivists and the Russian Revolution in Art and Architecture». The Guardian. Consultado el 6 June 2016. 
  37. ↑ El constructivismo influyó en la Bauhaus y Le Corbusier, por ejemplo.[36]​
  38. ↑ «Rietveld Schröderhuis (Rietveld Schröder House)». World Heritage Centre. Unesco. Consultado el 13 December 2012. 
  39. ↑ Historic England. «Details from listed building database (1358981)». National Heritage List for England. Consultado el 5 October 2015. 
  40. ↑ Moholy-Nagy, Laszlo; Hoffman, Daphne M. (trans.) (1938). The New Vision: Fundamentals of Design, Painting, Sculpture, Architecture. New Bauhaus Books. p. 46. 
  41. ↑ Gamwell, Lynn (2015). Mathematics and Art: A Cultural History. Princeton University Press. p. 306. ISBN 978-0-691-16528-8. 
  42. ↑ Le Corbusier (2004). The Modulor: A Harmonious Measure to the Human Scale, Universally Applicable to Architecture and Mechanics. Birkhäuser. ISBN 3-7643-6188-3.  Parámetro desconocido |orig-year= ignorado (ayuda)
  43. ↑ a b c Salingaros, Nikos. «Architecture, Patterns, and Mathematics». Nexus Network Journal. Consultado el 9 October 2015.  Updated version of Salingaros, Nikos (April 1999). «Architecture, Patterns, and Mathematics». Nexus Network Journal 1 (2): 75-86. S2CID 120544101. doi:10.1007/s00004-998-0006-0.  Parámetro desconocido |doi-access= ignorado (ayuda)
  44. ↑ Greene, Herb. «Le Corbusier: Notre Dame du Haut at Ronchamp». Archivado desde el original el 7 September 2015. Consultado el 5 October 2015.  Parámetro desconocido |url-status= ignorado (ayuda)
  45. ↑ Pace Nikos Salingaros, who suggests the contrary,[43]​ but it is not clear exactly what mathematics may be embodied in the curves of Le Corbusier's chapel.[44]​
  46. ↑ Hanser, David A. (2006). Architecture of France. Greenwood Publishing Group. p. 211. ISBN 978-0-313-31902-0. 
  47. ↑ «Vanity Fair's World Architecture Survey: the Complete Results». Vanity Fair. 30 June 2010. Consultado el 22 July 2010. 
  48. ↑ «Denver International Airport Press Kit». Denver International Airport. 2014. Archivado desde el original el 12 April 2015. Consultado el 5 October 2015.  Parámetro desconocido |url-status= ignorado (ayuda)
  49. ↑ «Denver International Airport». Fenstress Architects. Consultado el 5 October 2015. 
  50. ↑ «Biosphere». A view on cities. Consultado el 1 October 2015. 
  51. ↑ Hahn, Alexander J. (4 February 2013). «Mathematical Excursions To Architecture». Inside Science. Consultado el 5 October 2015. 
  52. ↑ Salingaros, Nikos (2006). A Theory of Architecture. Umbau. pp. 139-141. ISBN 9783937954073. 
  53. ↑ Salingaros, Nikos (2006). A Theory of Architecture. Umbau. pp. 124-125. ISBN 9783937954073. 
  54. ↑ Gehry, Frank O.; Mudford, Grant; Koshalek, Richard (2009). Symphony: Frank Gehry's Walt Disney Concert Hall. Five Ties. ISBN 9780979472749. 
  55. ↑ Garcetti, Gil (2004). Iron: Erecting the Walt Disney Concert Hall. Princeton Architectural Press. ISBN 9781890449285. 
  56. ↑ a b Bartlett, Christopher (2014). «The Design of The Great Pyramid of Khufu». Nexus Network Journal 16 (2): 299-311. doi:10.1007/s00004-014-0193-9.  Parámetro desconocido |doi-access= ignorado (ayuda)
  57. ↑ Markowsky, George (January 1992). «Misconceptions About the Golden Ratio». The College Mathematics Journal 23 (1): 2-19. doi:10.1080/07468342.1992.11973428. Archivado desde el original el 8 de abril de 2008. Consultado el 1 de octubre de 2015.  Parámetro desconocido |url-status= ignorado (ayuda)
  58. ↑ Livio, Mario (2003). The Golden Ratio: The Story of Phi, the World's Most Astonishing Number (First trade paperback edición). New York City: Broadway Books. p. 61. ISBN 0-7679-0816-3.  Parámetro desconocido |orig-year= ignorado (ayuda)
  59. ↑ Gazalé, Midhat (1999). Gnomon: From Pharaohs to Fractals. Princeton University Press. [página requerida]
  60. ↑ a b c d Cooke, Roger L. (2011). The History of Mathematics: A Brief Course (2nd edición). John Wiley & Sons. pp. 237-238. ISBN 978-1-118-03024-0. 
  61. ↑ Gillings, Richard J. (1982). Mathematics in the Time of the Pharaohs. Dover. p. 161. (requiere registro). 
  62. ↑ Berlin Papyrus 6619 from the Middle Kingdom stated that "the area of a square of 100 is equal to that of two smaller squares. The side of one is ½ + ¼ the side of the other."
  63. ↑ Kramrisch, Stella (1976), The Hindu Temple Volume 1 & 2, ISBN 81-208-0223-3
  64. ↑ Vibhuti Sachdev, Giles Tillotson (2004). Building Jaipur: The Making of an Indian City. pp. 155-160. ISBN 978-1-86189-137-2. 
  65. ↑ Ifrah, Georges (1998). A Universal History of Numbers. Penguin. 
  66. ↑ a b «Fractals in Indian Architecture». Yale University. Archivado desde el original el 6 February 2012. Consultado el 1 October 2015.  Parámetro desconocido |url-status= ignorado (ayuda)
  67. ↑ Jackson, William J. «For All Fractal Purposes ... an introduction». Indiana University-Purdue University Indianapolis. Archivado desde el original el 14 September 2015. Consultado el 1 October 2015. 
  68. ↑ King, Anthony D. (2005). Buildings and Society: Essays on the Social Development of the Built Environment. Taylor & Francis. p. 72. ISBN 0-203-48075-9. 
  69. ↑ Maor, Eli (2007). The Pythagorean Theorem: A 4,000-year History. Princeton University Press. p. 19. ISBN 978-0-691-12526-8. 
  70. ↑ a b Norwich, John Julius (2001). Great Architecture of the World. Artists House. p. 63. 
  71. ↑ Penrose, Francis (1973). Principles of Athenian Architecture. Society of Dilettanti. p. ch. II.3, plate 9.  Parámetro desconocido |orig-year= ignorado (ayuda)
  72. ↑ Stevens, Gorham P. (July 1962). «Concerning the Impressiveness of the Parthenon». American Journal of Archaeology 66 (3): 337-338. JSTOR 501468. doi:10.2307/501468. 
  73. ↑ Euclid. Elements. Book 6, Proposition 30.
  74. ↑ Archibald, R. C. «Notes on the Logarithmic Spiral, Golden Section and the Fibonacci Series». Consultado el 1 October 2015. 
  75. ↑ Applications of the Golden Mean to Architecture
  76. ↑ Markowsky, George (January 1992). «Misconceptions about the Golden Ratio». The College Mathematics Journal 23 (1): 2-19. doi:10.1080/07468342.1992.11973428. Archivado desde el original el 8 de abril de 2008. Consultado el 1 de octubre de 2015.  Parámetro desconocido |url-status= ignorado (ayuda)
  77. ↑ Gedal, Najib. «The Great Mosque of Cordoba: Geometric Analysis». Islamic Art & Architecture. Archivado desde el original el 2 October 2015. Consultado el 16 October 2015.  Parámetro desconocido |url-status= ignorado (ayuda)
  78. ↑ Irwin, Robert (26 de mayo de 2011). The Alhambra. Profile Books. pp. 109-112. ISBN 978-1-84765-098-6. 
  79. ↑ Robertson, Ann (2007). «Revisiting the Geometry of the Sala de Dos Hermanas». BRIDGES. Consultado el 11 October 2015. 
  80. ↑ Blair, Sheila; Bloom, Jonathan M. (1995). The Art and Architecture of Islam 1250–1800. Yale University Press. ISBN 0-300-06465-9. 
  81. ↑ Michell, George; Pasricha, Amit (2011). Mughal Architecture & Gardens. Antique Collectors Club. ISBN 978-1-85149-670-9. 
  82. ↑ Parker, Philip (2010). World History. Dorling Kindersley. p. 224. ISBN 978-1-4053-4124-0. 
  83. ↑ Koch, Ebba (2006). The Complete Taj Mahal: And the Riverfront Gardens of Agra (1st edición). Thames & Hudson. pp. 24 and passim. ISBN 0-500-34209-1. (requiere registro). 
  84. ↑ 1 gaz is about 0,86 metros (2,8 pies).
  85. ↑ A square drawn around the octagon by prolonging alternate sides adds four right angle triangles with hypotenuse of 7 and the other two sides of √49/2 or 4.9497..., nearly 5. The side of the square is thus 5+7+5, which is 17.
  86. ↑ Koch, Ebba (2006). The Complete Taj Mahal: And the Riverfront Gardens of Agra (1st edición). Thames & Hudson. pp. 104–109. ISBN 0-500-34209-1. (requiere registro). 
  87. ↑ Until Catedral de Sevilla was completed in 1520.
  88. ↑ Fazio, Michael; Moffett, Marian; Wodehouse, Lawrence (2009). Buildings Across Time (3rd edición). McGraw-Hill Higher Education. ISBN 978-0-07-305304-2. 
  89. ↑ Gamwell, Lynn (2015). Mathematics and Art: A Cultural History. Princeton University Press. p. 48. ISBN 978-0-691-16528-8. 
  90. ↑ Kleiner, Fred S.; Mamiya, Christin J. (2008). Gardner's Art Through the Ages: Volume I, Chapters 1–18 (12th edición). Wadsworth. p. 329. ISBN 978-0-495-46740-3. 
  91. ↑ Menander, Hanna; Brandt, Olof; Appetechia, Agostina; Thorén, Håkan (2010). «The Lateran Baptistery in Three Dimensions». Swedish National Heritage Board. Consultado el 30 October 2015. 
  92. ↑ «The Baptistery». The Leaning Tower of Pisa. Consultado el 30 October 2015. 
  93. ↑ a b Huyser-Konig, Joan. «Theological Reasons for Baptistry Shapes». Calvin Institute of Christian Worship. Consultado el 30 October 2015. 
  94. ↑ The sixth day of Semana Santa was Viernes Santo; the following Sunday (of the resurrección) was thus the eighth day.[93]​
  95. ↑ a b Kuehn, Regina (1992). A Place for Baptism. Liturgy Training Publications. pp. 53-60. ISBN 978-0-929650-00-5. 
  96. ↑ Augustine of Hippo (426). The City of God. p. Book 22, Chapter 30.  Parámetro desconocido |title-link= ignorado (ayuda)
  97. ↑ Kleiner, Fred (2012). Gardner's Art through the Ages: A Global History. Cengage Learning. pp. 355-356. ISBN 978-1-133-71116-2. 
  98. ↑ a b c Simitch, Andrea; Warke, Val (2014). The Language of Architecture: 26 Principles Every Architect Should Know. Rockport Publishers. p. 191. ISBN 978-1-62788-048-0. 
  99. ↑ «Zelená hora near Žďár nad Sázavou». Czech Tourism. Consultado el 10 November 2015. 
  100. ↑ «Attributes of Saint John of Nepomuk». Saint John of Nepomuk. Archivado desde el original el 4 March 2016. Consultado el 10 November 2015.  Parámetro desconocido |url-status= ignorado (ayuda)
  101. ↑ Burry, M.C., J.R. Burry, G.M. Dunlop and A. Maher (2001). «Drawing Together Euclidean and Topological Threads (pdf)». Presented at SIRC 2001 – the Thirteenth Annual Colloquium of the Spatial Information Research Center. Dunedin, New Zealand: University of Otago. Archivado desde el original el 31 de octubre de 2007. Consultado el 28 de noviembre de 2007. 
  102. ↑ «The Geometry of Antoni Gaudi». Math & the Art of MC Escher. Saint Louis University Mathematics and Computer Science. Consultado el 4 October 2015. 
  103. ↑ Usvat, Liliana. «Antony Gaudi and Mathematics». Mathematics Magazine. Consultado el 4 October 2015. 
  104. ↑ M.C. Burry; J.R. Burry; G.M. Dunlop; A. Maher (2001). Drawing Together Euclidean and Topological Threads. The 13th Annual Colloquium of the Spatial Information Research Centre, University of Otago, Dunedin, New Zealand. Archivado desde el original el 25 June 2008. Consultado el 5 August 2008. 
  105. ↑ Nervi, Pier Luigi. «Cathedral of Saint Mary of the Assumption». Architectuul. Consultado el 12 October 2015. 
  106. ↑ This is 90 toneladas (90,0 t).
  107. ↑ «Brasilia Cathedral». About Brasilia. Consultado el 13 November 2015. 
  108. ↑ Behrends, Ehrhard; Crato, Nuno; Rodrigues, Jose Francisco (2012). Raising Public Awareness of Mathematics. Springer Science & Business Media. p. 143. ISBN 978-3-642-25710-0. 
  109. ↑ Emmer, Michele (2012). Imagine Math: Between Culture and Mathematics. Springer Science & Business Media. p. 111. ISBN 978-88-470-2427-4. 
  110. ↑ Mkrtchyan, Ruzanna (2013). «Cathedral of Brasilia». Building.AM. Consultado el 13 November 2015. 
  111. ↑ «Østerlars kirke» (en danés). Nordens kirker. Consultado el 2 December 2016. 
  112. ↑ «Østerlars kirke» (en danés). Natur Bornholm. Archivado desde el original el 19 July 2011. Consultado el 2 December 2016.  Parámetro desconocido |url-status= ignorado (ayuda)
  113. ↑ a b Rønning, Frode. «Islamic Patterns And Symmetry Groups». University of Exeter. Consultado el 18 April 2014. 
  114. ↑ a b c Gibberd, Matt; Hill, Albert (20 August 2013). «The Return of Ornamentation». The Telegraph. Consultado el 12 October 2015. 
  115. ↑ «Ravensbourne College by Foreign Office Architects». de zeen magazine. 13 September 2010. Consultado el 12 October 2015. 
  116. ↑ a b Bizley, Graham. «FOA's peninsula patterns for Ravensbourne College». bdonline.co.uk. Consultado el 16 October 2015. 
  117. ↑ An aperiodic tiling was considered, to avoid the rhythm of a structural grid, but in practice a Penrose tiling was too complex, so a grid of 2.625m horizontally and 4.55m vertically was chosen.[116]​
  118. ↑ Duffy, C. (1975). Fire & Stone, The Science of Fortress Warfare 1660–1860. Booksales. ISBN 978-0-7858-2109-0. 
  119. ↑ Chandler, David (1990). The Art of Warfare in the Age of Marlborough. Spellmount. ISBN 978-0-946771-42-4. 
  120. ↑ Giedion, Siegfried (1962). Space, Time and Architecture. Harvard University Press. p. 43.  Parámetro desconocido |orig-year= ignorado (ayuda)
  121. ↑ O'Neill, Tom (4 January 2015). «China's Remote Fortresses Lose Residents, Gain Tourists». National Geographic. Consultado el 6 January 2017. 
  122. ↑ Mahdavinejad, M.; Javanrudi, Kavan (July 2012). «Assessment of Ancient Fridges: A Sustainable Method to Storage Ice in Hot-Arid Climates». Asian Culture and History 4 (2). doi:10.5539/ach.v4n2p133.  Parámetro desconocido |doi-access= ignorado (ayuda)

Referencias

Enlaces externos

Obtenido de «https://es.wikipedia.org/w/index.php?title=Matemáticas_y_arquitectura&oldid=135759759»