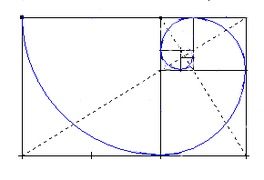
Rectángulo dorado

El rectángulo dorado (denominado también rectángulo áureo) es un rectángulo que posee una proporcionalidad entre sus lados igual a la razón áurea.[1] Es decir que es aquel rectángulo que al substraer la imagen de un cuadrado igual al de su lado menor, el rectángulo resultante es igualmente un rectángulo dorado. A partir de este rectángulo se puede obtener la espiral dorada, que es una espiral logarítmica.
Construcción[editar]

En la matemática clásica se construye a partir de la regla y compás siguiendo los pasos:
- Se construye un cuadrado de lado unidad ABCD
- Traza una línea desde la mitad del lado del cuadrado (G) hasta una de sus esquinas, dando un segmento GC
- Empleando esta línea GC como radio, se coloca la punta del compás en la mitad del cuadrado y se abate hasta cortar en E.
- Se completa el rectángulo AEDF así como el rectángulo BCEF.
Desarrollos[editar]
De acuerdo con el matemático y divulgador científico Mario Greco, desde la publicación del libro de Luca Pacioli titulado Divina Proportione in 1509,[2] Fue cuando la razón dorada aparece descrita en los tratados de arte y de arquitectura,"[3] haciendo que muchos artistas y arquitectos emplearan su cantidad en el diseño por considerarlo estéticamente agradable.[4]
Algebraica[editar]
Si la longitud del lado mayor se denomina x, se tiene entonces por definición que se respeta la siguiente igualdad:
Esto lleva a tener que resolver la ecuación de segundo grado:
En la que una de las dos raíces es la proporción dorada.
El rectángulo de Euclides[editar]
 Se trata de una de las demostraciones más conocidas desde la antigüedad. El rectángulo cuyos vértices se definen por los puntos AEFD se define como áureo debido a que sus lado mayor AE y su lado corto AD presentan la proporción del número áureo. El matemático griego Euclides, en su proposición 2.11 de la obra Los elementos, obtiene su construcción. Siendo el triángulo GBC pitagórico, se tiene que GC (la hipotenusa) tiene como valor:
Se trata de una de las demostraciones más conocidas desde la antigüedad. El rectángulo cuyos vértices se definen por los puntos AEFD se define como áureo debido a que sus lado mayor AE y su lado corto AD presentan la proporción del número áureo. El matemático griego Euclides, en su proposición 2.11 de la obra Los elementos, obtiene su construcción. Siendo el triángulo GBC pitagórico, se tiene que GC (la hipotenusa) tiene como valor:
Con centro en G, prolongando hasta la recta AE, se obtiene por intersección el punto E, y por lo tanto:
con todo ello se puede ver que resulta evidente que los lados:
de donde, finalmente:
Por otra parte, los rectángulos AEFD y BEFC son semejantes, de modo que este último es asimismo un rectángulo áureo.
Generación[editar]
| Rectángulo | |||||||||
| |||||||||
El rectángulo dorado en la industria[editar]
- La norma DIN 476 es la que define la medida del DIN A4 y otros tamaños de papel. El DIN A4 y sus derivados A3, A2... no mantienen las proporciones del rectángulo dorado, sino que mantienen la relación √2 = 1.4142
En la arquitectura[editar]
El rectángulo áureo fue calificado por los griegos de la clásica Hélade como una de las figuras geométricas más bellamente estructuradas. Por un largo lapso de siglos, los arquitectos utilizaron este cuadrilátero de noble proporción para la planeación de templos, rascacielos y edificaciones de diversa índole. Los compatriotas de Sócrates construyeron el Partenón de Atenas en el siglo V a. C. El rectángulo que encierra la fachada delantera es un rectángulo áureo.[5]
Referencias[editar]
- ↑ Livio, Mario (2002). Editorial Ariel, ed. La proporción áurea (Primera (Español) edición). Barcelona.
- ↑ Pacioli, Luca. De divina proportione, Luca Paganinem de Paganinus de Brescia (Antonio Capella) 1509, Venice.
- ↑ Livio, Mario (2002). The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. Nueva York: Broadway Books. ISBN 0-7679-0815-5.
- ↑ Van Mersbergen, Audrey M., Rhetorical Prototypes in Architecture: Measuring the Acropolis with a Philosophical Polemic, Communication Quarterly, Vol. 46, 1998 ("a 'Golden Rectangle' has a ratio of the length of its sides equal to 1:1.61803+. The Parthenon is of these dimensions.")
- ↑ Clemens y coautores: «Geometría /con aplicaciones y solución de problemas» ISBN 0-201-64407-X
Véase también[editar]
Referencias externas[editar]
 Wikimedia Commons alberga una categoría multimedia sobre Rectángulo dorado.
Wikimedia Commons alberga una categoría multimedia sobre Rectángulo dorado.