Politopo uniforme

Politopos uniformes convexos

2D	3D
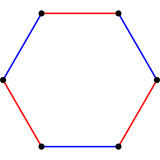Triángulo truncado o hexágono uniforme, con diagrama de Coxeter-Dynkin 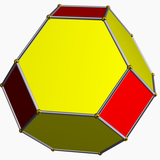.	Octaedro truncado,
4D	5D
16-celdas truncado,	5-ortoplex truncado,

En geometría, un politopo uniforme de dimensión tres o superior es una forma geométrica isogonal delimitada por un facetas uniformes. Los politopos uniformes en dos dimensiones son los polígonos regulares (la definición es diferente en 2 dimensiones, para excluir a los polígonos de lados pares vértice-transitivos que alternan dos longitudes diferentes de aristas).

Esta es una generalización de la categoría anterior de politopos semirregulares, pero también incluye los politopos regulares. Además, se permiten tanto caras regulares como figuras de vértice con forma de estrella (polígonos estrellados), lo que amplía enormemente las posibles soluciones. Una definición estricta requiere que los politopos uniformes sean finitos, mientras que una definición más amplia permite que los panales uniformes (teselados bidimensionales y panales de dimensiones superiores) de los espacios euclídeo e hiperbólico también se consideren politopos.​

Operaciones

Casi todos los politopos uniformes pueden generarse mediante un Construcción de Wythoff y representarse mediante un Diagrama de Coxeter-Dynkin. Las excepciones notables incluyen el great dirhombicosidodecahedron en tres dimensiones y el gran antiprisma en cuatro dimensiones. La terminología para los politopos uniformes convexos utilizados en los artículos poliedro uniforme, uniform 4-polytope, uniform 5-polytope, uniform 6-polytope, uniform tiling y convex uniform honeycomb fue acuñada por Norman Johnson. ^{[cita requerida]}

De manera equivalente, los politopos wythoffianos se pueden generar aplicando operaciones básicas a los politopos regulares en esa dimensión. Este enfoque fue utilizado por primera vez por Johannes Kepler y es la base de Notación de poliedros de Conway.

Operadores de rectificación

Los n-politopos regulares tienen n órdenes de rectification. La rectificación cero es la forma original. La (n−1)-ésima rectificación es la dual. Una rectificación reduce las aristas a vértices, una birectificación reduce las caras a vértices, una trirectificación reduce las celdas a vértices, una quadirectificación reduce 4- caras a vértices, una quintirectificación reducida de 5 caras a vértices, y así sucesivamente.

Se puede utilizar un Símbolo de Schläfli extendido para representar formas rectificadas, con un solo subíndice:

• k-ésima rectificación = t_k{p₁, p₂, ..., p_n-1} = kr.

Operadores de truncamiento

Operaciones de truncamiento que se pueden aplicar a n-politopos regulares en cualquier combinación. El diagrama de Coxeter resultante tiene dos nodos anillados y la operación recibe el nombre de la distancia entre ellos. Truncamiento corta vértices, cantelación' corta bordes, runcinación corta caras, estericación corta células. Cada operación superior también corta las inferiores, por lo que una cantelación también trunca los vértices.

1. t_0,1 o t: Truncation: se aplica a polígono y superiores. Un truncamiento elimina los vértices e inserta una nueva faceta en lugar de cada vértice anterior. Las caras se truncan, duplicando sus aristas. (El término, acuñado por Johannes Kepler, proviene del latín "truncare", "cortar".)

   

   • También hay truncamientos superiores: bitruncation't_1,2 o 2t, tritruncamiento't_2,3 o 3t , cuatritruncamiento t_3,4 o 4t, quintitruncado t_4,5 o 5t, etc.
2. t_0,2 o rr: Cantellation: se aplica a polyhedra y superiores. Puede verse como una rectificación de su rectification. Una cantelación trunca tanto los vértices como las aristas y los reemplaza con nuevas facetas. Las células son reemplazadas por copias topológicamente expanded de sí mismas. (El término, acuñado por Johnson, se deriva del verbo "cant", como "bisel (borde)", que significa cortar con la cara inclinada).

   

   • También hay cantelaciones superiores: bicantellation t_1,3 o r2r, tricantellation t_2,4 o r3r , cuadricantelación t_3,5 o r4r, etc.
   • t_0,1,2 o tr: Cantitruncation - aplicado a polyhedra y superiores. Se puede considerar que trunca su rectification. Un cantitruncado trunca tanto los vértices como las aristas y los reemplaza con nuevas facetas. Las células son reemplazadas por copias topológicamente expanded de sí mismas. (El término compuesto combina cantelación y truncamiento)
     • También hay cantelaciones superiores: bicantitruncation t_1,2,3 o t2r, tricantitruncation t_2,3,4 o t3r, quadricantitruncation t_3,4,5 o t4r, etc.
3. t_0,3: Runcinado - se aplica a Uniform 4-polytope y superiores. Runcination trunca vértices, aristas y caras, reemplazándolos cada uno con nuevas facetas. Las 4 caras son reemplazadas por copias topológicamente expandidas de sí mismas. (El término, acuñado por Johnson, se deriva del latín runcina, 'plane del carpintero'.)
   • También hay runcinaciones superiores: biruncination t_1,4, triruncination t_2,5, etc.
4. t_0,4 o 2r2r: Sterication: se aplica a Uniform 5-polytope y superiores. Puede verse como una birectificación de su birectificación. La estericación trunca vértices, aristas, caras y celdas, reemplazando cada uno con nuevas facetas. Las 5 caras son reemplazadas por copias topológicamente expandidas de sí mismas. (El término, acuñado por Johnson, se deriva del griego "estéreo", "sólido".)
   • También hay estericaciones superiores: bistericación t_1,5 o 2r3r, tristericación t_2,6 o 2r4r , etc.
   • t_0,2,4 o 2t2r: Estericantelación: se aplica a Uniform 5-polytope y superiores. Puede verse como el bitruncado

descifrando su birectificación.

1. • • También hay estericaciones superiores: bistericantellation' t_1,3,5 o 2t3r, tristericantellation t_2,4,6 o 2t4r, etc.
2. t_0,5: Pentelation: se aplica a Uniform 6-polytope y superiores. La pentelación trunca vértices, aristas, caras, celdas y 4 caras, reemplazando cada uno con nuevas facetas. Las 6 caras son reemplazadas por copias topológicamente expandidas de sí mismas. (La pentelación se deriva del griego pente 'cinco').
   • También hay pentelaciones superiores: bipentellation t_1,6, tripentellation t_2,7, etc.
3. t_0,6 o 3r3r: Hexificación: se aplica a Uniform 7-polytope y superiores. Puede verse como una trirectificación de su trirectificación. La hexicación trunca vértices, aristas, caras, celdas, 4 caras y 5 caras, reemplazando cada uno con nuevas facetas. Las 7 caras son reemplazadas por copias topológicamente expandidas de sí mismas. (La hexicación se deriva del griego hex, 'seis'.)
   • También hay hexicaciones superiores: bihexication': t_1,7 o 3r4r, trihexication: t_2,8 o '3r5r, etc.
   • t_0,3,6 o 3t3r: Hexiruncinated - aplicado a Uniform 7-polytope y superiores. Puede verse como un tritruncamiento de su trirectificación.
     • También hay hexiruncinaciones superiores: bihexiruncinated': t_1,4,7 o 3t4r, trihexiruncinated: t_2,5,8 o ' 3t5r, etc.
4. t_0,7: Heptellation: se aplica a Uniform 8-polytope y superiores. La heptelación trunca vértices, aristas, caras, celdas, 4 caras, 5 caras y 6 caras, reemplazando cada una con nuevas facetas. Las 8 caras son reemplazadas por copias topológicamente expandidas de sí mismas. (La heptelación se deriva del griego hepta 'siete').
   • También hay heptelaciones superiores: biheptellation t_1,8, triheptellation t_2,9, etc.
5. t_0,8 o 4r4r: Octellation: se aplica a Uniform 9-polytope y superiores.
6. t_0,9: Ennecation: se aplica a Uniform 10-polytope y superiores.

Además, se pueden realizar combinaciones de truncamientos que también generan nuevos politopos uniformes. Por ejemplo, un "runcitruncamiento" es un "runcinación" y un "truncamiento" aplicados juntos.

Si se aplican todos los truncamientos a la vez, la operación puede denominarse de manera más general omnitruncation.

Alternancia

An alternation of a cuboctaedro truncado produces a cubo romo.

Una operación especial, llamada alternation, elimina vértices alternativos de un politopo que solo tiene caras pares. Un politopo omnitruncado alterno se llama "desaire".

Los politopos resultantes siempre se pueden construir, y generalmente no son reflectantes y, en general, tampoco tienen soluciones de politopos "uniformes".

El conjunto de politopos formados alternando los hipercubo se conocen como tetraedro. En tres dimensiones, esto produce un tetraedro; en cuatro dimensiones, esto produce un hexadecacoron, o demitesseract.

Figura de vértice

Se pueden construir politopos uniformes a partir de su figura de vértice, la disposición de aristas, caras, celdas, etc. alrededor de cada vértice. Los politopos uniformes representados por un Diagrama de Coxeter-Dynkin, que marcan espejos activos mediante anillos, tienen simetría reflexiva y pueden construirse simplemente mediante reflexiones recursivas de la figura del vértice.

Un número menor de politopos uniformes no reflexivos tienen una única figura de vértice pero no se repiten mediante reflexiones simples. La mayoría de estos se pueden representar con operaciones como alternation de otros politopos uniformes.

Las figuras de vértice para diagramas de Coxeter de anillo único se pueden construir a partir del diagrama eliminando el nodo anillado y haciendo sonar los nodos vecinos. Estas figuras de vértice son en sí mismas transitivas por vértice.

Los politopos de anillos múltiples se pueden construir mediante un proceso de construcción un poco más complicado y su topología no es un politopo uniforme. Por ejemplo, la figura del vértice de un politopo regular truncated (con 2 anillos) es una pirámide. Un politopo omnitruncated (todos los nodos anillados) siempre tendrá un símplex irregular como figura de vértice.

Circunradio

Los politopos uniformes tienen aristas de igual longitud y todos los vértices están a la misma distancia del centro, lo que se denomina circunradio.

Los politopos uniformes cuyo circunradio es igual a la longitud del borde se pueden utilizar como figura de vértice para uniform honeycomb. Por ejemplo, el hexágono regular se divide en 6 triángulos equiláteros y es la figura de vértice del teselado triangular regular. Además, el cuboctaedro se divide en 8 tetraedros regulares y 6 pirámides cuadradas (la mitad de octaedro), y es la figura del vértice del alternated cubic honeycomb.

Politopos uniformes por dimensión

Es útil clasificar los politopos uniformes por dimensión. Esto equivale al número de nodos en el diagrama de Coxeter, o al número de hiperplanos en la construcción Wythoffiana. Debido a que los politopos de (n+1) dimensiones son mosaicos de espacio esférico de n dimensiones, los mosaicos de Euclidean y espacio hiperbólico de n dimensiones también se consideran (n+ 1)-dimensional. Por tanto, los mosaicos del espacio bidimensional se agrupan con los sólidos tridimensionales.

Una dimensión

El único politopo unidimensional es el segmento de recta. Corresponde a la familia Coxeter A₁.

Dos dimensiones

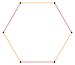
En dos dimensiones, existe una familia infinita de politopos uniformes convexos, los polígono regular, siendo el más simple el triángulo equilátero. Los polígonos regulares truncados se convierten geométricamente en polígonos bicolores quasiregular del doble de lados, t{p}={2p}. Los primeros polígonos regulares (y formas cuasiregulares) se muestran a continuación:

Name	Triangle (2-simplex)	Square (2-orthoplex) (2-cube)	Pentágono	Hexágono	Heptágono	Octógono	Eneágono	Decágono	Endecágono
Schläfli	{3}	{4} t{2}	{5}	{6} t{3}	{7}	{8} t{4}	{9}	{10} t{5}	{11}
Coxeter diagram
Image
Name	Dodecágono	Tridecágono	Tetradecágono	Pentadecágono	Hexadecágono	Heptadecágono	Octodecágono	Polígono	Isodecágono
Schläfli	{12} t{6}	{13}	{14} t{7}	{15}	{16} t{8}	{17}	{18} t{9}	{19}	{20} t{10}
Coxeter diagram
Imagen

También hay un conjunto infinito de estrella (figura geométrica) (uno por cada número racional mayor que 2), pero no son convexos. El ejemplo más sencillo es el estrella pentagonal, que corresponde al número racional 5/2. Los polígonos de estrellas regulares, {p/q}, se pueden truncar en polígonos de estrellas semirregulares, t{p/q}=t{2p/q}, pero se convierten en coberturas dobles si "q" es par. También se puede realizar un truncamiento con un polígono de orientación inversa t{p/(p-q)}={2p/(p-q)}, por ejemplo t{5/3}={10/3}.

Name	Estrella pentagonal	Heptagramas		Octagrama	Enneagrams		Decagram	...n-agrams
Schläfli	{5/2}	{7/2}	{7/3}	{8/3} t{4/3}	{9/2}	{9/4}	{10/3} t{5/3}	{p/q}
Coxeter diagram
Imagen

Polígonos regulares, representados por Símbolo de Schläfli {p} para un p-gon. Los polígonos regulares son autoduales, por lo que la rectificación produce el mismo polígono. La operación de truncamiento uniforme duplica los lados a {2p}. La operación de desaire, alternando el truncamiento, restaura el polígono original {p}. Por tanto, todos los polígonos uniformes también son regulares. Se pueden realizar las siguientes operaciones en polígonos regulares para derivar polígonos uniformes, que también son polígonos regulares:

Operation	Extended Schläfli Symbols		Regular result	Coxeter diagram	Position		Symmetry
					(1)	(0)
Parent	{p}	t0{p}	{p}		{}	--	[p] (order 2p)
Rectified (Dual)	r{p}	t1{p}	{p}		--	{}	[p] (order 2p)
Truncated	t{p}	t0,1{p}	{2p}		{}	{}	[[p]]=[2p] (order 4p)
Half	h{2p}		{p}		--	--	[1+,2p]=[p] (order 2p)
Snub	s{p}		{p}		--	--	[[p]]+=[p] (order 2p)

Tres dimensiones

En tres dimensiones, la situación se vuelve más interesante. Hay cinco poliedros regulares convexos, conocidos como Sólidos platónicos:

Name	Schläfli {p,q}	Diagram	Image (transparent)	Image (solid)	Image (sphere)	Faces {p}	Edges	Vertices {q}	Symmetry	Dual
Tetraedro (3-simplex) (Pyramid)	{3,3}					4 {3}	6	4 {3}	Td	(self)
Cubo (3-cube) (Hexahedron)	{4,3}					6 {4}	12	8 {3}	Oh	Octahedron
Octaedro (3-orthoplex)	{3,4}					8 {3}	12	6 {4}	Oh	Cube
Dodecaedro	{5,3}					12 {5}	30	20 {3}2	Ih	Icosahedron
Icosaedro	{3,5}					20 {3}	30	12 {5}	Ih	Dodecahedron

Además de estos, también hay 13 poliedros semirregulares, o Sólidos arquimedianos, que se pueden obtener mediante Construcción de Wythoff o realizando operaciones como truncation en los sólidos platónicos, como se demuestra en la siguiente tabla:

	Parent	Truncated	Rectified	Bitruncated (tr. dual)	Birectified (dual)	Cantellated	Omnitruncated (Cantitruncated)	Snub
Tetrahedral 3-3-2	{3,3}	(3.6.6)	(3.3.3.3)	(3.6.6)	{3,3}	(3.4.3.4)	(4.6.6)	(3.3.3.3.3)
Octahedral 4-3-2	{4,3}	(3.8.8)	(3.4.3.4)	(4.6.6)	{3,4}	(3.4.4.4)	(4.6.8)	(3.3.3.3.4)
Icosahedral 5-3-2	{5,3}	(3.10.10)	(3.5.3.5)	(5.6.6)	{3,5}	(3.4.5.4)	(4.6.10)	(3.3.3.3.5)

También existe el conjunto infinito de prisms, uno para cada polígono regular, y un conjunto correspondiente de antiprisma.

#	Name	Picture	Tiling	Vertex figure	Diagram and Schläfli symbols
P2p	Prism				tr{2,p}
Ap	Antiprisma				sr{2,p}

Los poliedros estelares uniformes incluyen otros 4 poliedros estelares regulares, el Sólido de Kepler-Poinsot, y 53 poliedros estelares semirregulares. También hay dos conjuntos infinitos, los prismas estelares (uno por cada polígono estelar) y los antiprismas estelares (uno por cada número racional mayor que 3/2).

Construcciones

Los poliedros y mosaicos uniformes de Wythoff se pueden definir por su Símbolo de Wythoff, que especifica el dominio fundamental del objeto. Una extensión de la notación Schläfli, también utilizada por Coxeter, se aplica a todas las dimensiones; consta de la letra 't', seguida de una serie de números con subíndices correspondientes a los nodos anillados del Diagrama de Coxeter-Dynkin, y seguido del símbolo Schläfli del politopo de semillas regular. Por ejemplo, octaedro truncado se representa con la notación: t_0,1{3,4}.

Operation	Schläfli Symbol			Coxeter diagram		Wythoff symbol	Position:
Parent	${\begin{Bmatrix}p,q\end{Bmatrix}}$	{p,q}	t0{p,q}			q | 2 p	{p}	{}	--	--	--	{}
Birectified (or dual)	${\begin{Bmatrix}q,p\end{Bmatrix}}$	{q,p}	t2{p,q}			p | 2 q	--	{}	{q}	{}	--	--
Truncated	$t{\begin{Bmatrix}p,q\end{Bmatrix}}$	t{p,q}	t0,1{p,q}			2 q | p	{2p}	{}	{q}	--	{}	{}
Bitruncated (or truncated dual)	$t{\begin{Bmatrix}q,p\end{Bmatrix}}$	t{q,p}	t1,2{p,q}			2 p | q	{p}	{}	{2q}	{}	{}	--
Rectified	${\begin{Bmatrix}p\\q\end{Bmatrix}}$	r{p,q}	t1{p,q}			2 | p q	{p}	--	{q}	--	{}	--
Cantellated (or expanded)	$r{\begin{Bmatrix}p\\q\end{Bmatrix}}$	rr{p,q}	t0,2{p,q}			p q | 2	{p}	{}×{}	{q}	{}	--	{}
Cantitruncated (or Omnitruncated)	$t{\begin{Bmatrix}p\\q\end{Bmatrix}}$	tr{p,q}	t0,1,2{p,q}			2 p q |	{2p}	{}×{}	{2q}	{}	{}	{}

Operation	Schläfli Symbol			Coxeter diagram		Wythoff symbol	Position:
Snub rectified	$s{\begin{Bmatrix}p\\q\end{Bmatrix}}$	sr{p,q}				| 2 p q	{p}	{3} {3}	{q}	--	--	--
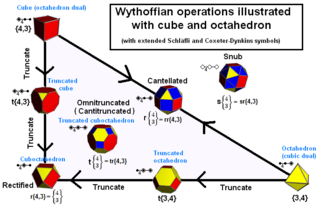
Snub	$s{\begin{Bmatrix}p,q\end{Bmatrix}}$	s{p,2q}	ht0,1{p,q}				s{2p}	{3}	{q}	--	{3}

Generating triangles

Cuatro dimensiones

En cuatro dimensiones, hay 6 convex regular 4-polytope, 17 prismas en los sólidos platónico y de Arquímedes (excluyendo el cubo-prisma, que ya se ha contado como teseracto) y dos conjuntos infinitos: los prismas en los antiprismas convexos y los duoprism. También hay 41 4 politopos semirregulares convexos, incluidos el construcción de Wythoff gran antiprisma y el snub 24-cell. Ambos politopos especiales de 4 están compuestos por subgrupos de los vértices del hexacosicoron.

No se han enumerado todos los politopos estelares uniformes de cuatro dimensiones. Los que tienen incluyen los 10 4 politopos de estrellas regulares (Schläfli-Hess) y 57 prismas en los poliedros estelares uniformes, así como tres familias infinitas: los prismas en los antiprismas estelares, los duoprismas formados por dos polígonos estelares multiplying, y los duoprismas se forman multiplicando un polígono ordinario por un polígono estrella. Hay un número desconocido de 4 politopos que no encajan en las categorías anteriores; Hasta ahora se han descubierto más de mil.

Example tetrahedron in cubic honeycomb cell.
There are 3 right dihedral angles (2 intersecting perpendicular mirrors):
Edges 1 to 2, 0 to 2, and 1 to 3.

Summary chart of truncation operations

Cada politopo regular puede verse como imágenes de un dominio fundamental en una pequeña cantidad de espejos. En un politopo de 4 dimensiones (o panal cúbico de 3 dimensiones), la región fundamental está delimitada por cuatro espejos. Un espejo en el espacio 4 es un hiperplano tridimensional, pero para nuestros propósitos es más conveniente considerar solo su intersección bidimensional con la superficie tridimensional del n-esfera; por tanto, los espejos forman un tetraedro irregular.

Cada uno de los dieciséis regular 4-polytopes es generado por uno de los cuatro grupos de simetría, de la siguiente manera:

• grupo [3,3,3]: el pentácoron {3,3,3}, que es autodual;
• grupo [3,3,4]: hexadecacoron {3,3,4} y su dual teseracto {4,3,3};
• grupo [3,4,3]: el icositetracoron {3,4,3}, autodual;
• grupo [3,3,5]: hexacosicoron {3,3,5}, su dual hecatonicosacoron {5,3,3} y sus diez estelaciones regulares.
• grupo [3^1,1,1]: contiene solo miembros repetidos de la familia [3,3,4].

(Los grupos se nombran en Notación de Coxeter).

Ocho de los convex uniform honeycomb en el espacio tridimensional euclidiano se generan de manera análoga a partir del cubic honeycomb {4,3,4}, aplicando las mismas operaciones utilizadas para generar los 4 politopos uniformes de Wythoff.

Para una simetría simplex dada, un punto generador se puede colocar en cualquiera de los cuatro vértices, 6 aristas, 4 caras o el volumen interior. Sobre cada uno de estos 15 elementos hay un punto cuyas imágenes, reflejadas en los cuatro espejos, son los vértices de un 4 politopo uniforme.

Los símbolos Schläfli extendidos están formados por una t seguida de la inclusión de uno a cuatro subíndices 0,1,2,3. Si hay un subíndice, el punto generador está en una esquina de la

La región fundamental, es decir, un punto donde se encuentran tres espejos. Estas esquinas se anotan como

• 0: vértice del 4 politopo principal (centro de la celda del dual)
• 1': centro del borde del padre (centro de la cara del dual)
• 2: centro de la cara del padre (centro del borde del dual)
• 3: centro de la celda del padre (vértice del dual)

(Para los dos 4 politopos autoduales, "dual" significa un 4 politopo similar en posición dual). Dos o más subíndices significan que el punto generador está entre las esquinas indicadas.

Resumen constructivo

A continuación se resumen las 15 formas constructivas por familia. Las familias autoduales se enumeran en una columna y otras en dos columnas con entradas compartidas en los Diagrama de Coxeter-Dynkin simétricos. La última décima fila enumera las construcciones chatas de 24 celdas. Esto incluye todos los 4 politopos uniformes no prismáticos, excepto el construcción de Wythoff gran antiprisma, que no tiene familia Coxeter.

A4	BC4		D4	F4	H4
[3,3,3]	[4,3,3]		[3,31,1]	[3,4,3]	[5,3,3]
pentácoron {3,3,3}	hexadecacoron {3,3,4}	teseracto {4,3,3}	hexadecacoron {3,31,1}	icositetracoron {3,4,3}	hexacosicoron {3,3,5}	hecatonicosacoron {5,3,3}
rectified 5-cell r{3,3,3}	rectified 16-cell r{3,3,4}	rectified tesseract r{4,3,3}	rectified demitesseract r{3,31,1}	rectified 24-cell r{3,4,3}	rectified 600-cell r{3,3,5}	rectified 120-cell r{5,3,3}
truncated 5-cell t{3,3,3}	truncated 16-cell t{3,3,4}	truncated tesseract t{4,3,3}	truncated demitesseract t{3,31,1}	truncated 24-cell t{3,4,3}	truncated 600-cell t{3,3,5}	truncated 120-cell t{5,3,3}
cantellated 5-cell rr{3,3,3}	cantellated 16-cell rr{3,3,4}	cantellated tesseract rr{4,3,3}	cantellated demitesseract 2r{3,31,1}	cantellated 24-cell rr{3,4,3}	cantellated 600-cell rr{3,3,5}	cantellated 120-cell rr{5,3,3}
runcinated 5-cell t0,3{3,3,3}	runcinated 16-cell t0,3{3,3,4}	runcinated tesseract t0,3{4,3,3}		runcinated 24-cell t0,3{3,4,3}	runcinated 600-cell runcinated 120-cell t0,3{3,3,5}
bitruncated 5-cell t1,2{3,3,3}	bitruncated 16-cell 2t{3,3,4}	bitruncated tesseract 2t{4,3,3}	cantitruncated demitesseract 2t{3,31,1}	bitruncated 24-cell 2t{3,4,3}	bitruncated 600-cell bitruncated 120-cell 2t{3,3,5}
cantitruncated 5-cell tr{3,3,3}	cantitruncated 16-cell tr{3,3,4}	cantitruncated tesseract tr{4,3,3}	omnitruncated demitesseract tr{3,31,1}	cantitruncated 24-cell tr{3,4,3}	cantitruncated 600-cell tr{3,3,5}	cantitruncated 120-cell tr{5,3,3}
runcitruncated 5-cell t0,1,3{3,3,3}	runcitruncated 16-cell t0,1,3{3,3,4}	runcitruncated tesseract t0,1,3{4,3,3}	runcicantellated demitesseract rr{3,31,1}	runcitruncated 24-cell t0,1,3{3,4,3}	runcitruncated 600-cell t0,1,3{3,3,5}	runcitruncated 120-cell t0,1,3{5,3,3}
omnitruncated 5-cell t0,1,2,3{3,3,3}	omnitruncated 16-cell t0,1,2,3{3,3,4}	omnitruncated tesseract t0,1,2,3{3,3,4}		omnitruncated 24-cell t0,1,2,3{3,4,3}	omnitruncated 120-cell omnitruncated 600-cell t0,1,2,3{5,3,3}
	alternated cantitruncated 16-cell sr{3,3,4}		snub demitesseract sr{3,31,1}	Alternated truncated 24-cell s{3,4,3}

Formas truncadas

La siguiente tabla define los 15 formularios. Cada formulario trunctionPlantilla:Typo help inline puede tener de uno a cuatro tipos de celdas, ubicadas en las posiciones 0,1,2,3 como se definió anteriormente. Las celdas están etiquetadas mediante notación de truncamiento poliédrico.

• Un prisma n-gonal se representa como: {n}×{ }.
• El fondo verde se muestra en formularios que son equivalentes al padre o al dual.
• El fondo rojo muestra los truncamientos del padre y el azul los truncamientos del dual.

Operation	Schläfli symbol		Coxeter diagram	Cells by position:
				(3)	(2)	(1)	(0)
Parent	{p,q,r}	t0{p,q,r}		{p,q}	--	--	--
Rectified	r{p,q,r}	t1{p,q,r}		r{p,q}	--	--	{q,r}
Birectified (or rectified dual)	2r{p,q,r} = r{r,q,p}	t2{p,q,r}		{q,p}	--	--	r{q,r}
Trirectifed (or dual)	3r{p,q,r} = {r,q,p}	t3{p,q,r}		--	--	--	{r,q}
Truncated	t{p,q,r}	t0,1{p,q,r}		t{p,q}	--	--	{q,r}
Bitruncated	2t{p,q,r}	2t{p,q,r}		t{q,p}	--	--	t{q,r}
Tritruncated (or truncated dual)	3t{p,q,r} = t{r,q,p}	t2,3{p,q,r}		{q,p}	--	--	t{r,q}
Cantellated	rr{p,q,r}	t0,2{p,q,r}		rr{p,q}	--	{}×{r}	r{q,r}
Bicantellated (or cantellated dual)	r2r{p,q,r} = rr{r,q,p}	t1,3{p,q,r}		r{p,q}	{p}×{}	--	rr{q,r}
Runcinated (or expanded)	e{p,q,r}	t0,3{p,q,r}		{p,q}	{p}×{}	{}×{r}	{r,q}
Cantitruncated	tr{p,q,r}	tr{p,q,r}		tr{p,q}	--	{}×{r}	t{q,r}
Bicantitruncated (or cantitruncated dual)	t2r{p,q,r} = tr{r,q,p}	t1,2,3{p,q,r}		t{q,p}	{p}×{}	--	tr{q,r}
Runcitruncated	et{p,q,r}	t0,1,3{p,q,r}		t{p,q}	{2p}×{}	{}×{r}	rr{q,r}
Runcicantellated (or runcitruncated dual)	e3t{p,q,r} = et{r,q,p}	t0,2,3{p,q,r}		tr{p,q}	{p}×{}	{}×{2r}	t{r,q}
Runcicantitruncated (or omnitruncated)	o{p,q,r}	t0,1,2,3{p,q,r}		tr{p,q}	{2p}×{}	{}×{2r}	tr{q,r}

Medias formas

Existen medias construcciones con "agujeros" en lugar de nodos anillados. Las ramas vecinas a los "agujeros" y a los nodos inactivos deben estar en orden par. La mitad de la construcción tiene los vértices de una construcción con anillos idénticos.

Operation	Schläfli symbol		Coxeter diagram	Cells by position:
				(3)	(2)	(1)	(0)
Half Alternated	h{p,2q,r}	ht0{p,2q,r}		h{p,2q}	--	--	--
Alternated rectified	hr{2p,2q,r}	ht1{2p,2q,r}		hr{2p,2q}	--	--	h{2q,r}
Snub Alternated truncation	s{p,2q,r}	ht0,1{p,2q,r}		s{p,2q}	--	--	h{2q,r}
Bisnub Alternated bitruncation	2s{2p,q,2r}	ht1,2{2p,q,2r}		s{q,2p}	--	--	s{q,2r}
Snub rectified Alternated truncated rectified	sr{p,q,2r}	ht0,1,2{p,q,2r}		sr{p,q}	--	s{2,2r}	s{q,2r}
Omnisnub Alternated omnitruncation	os{p,q,r}	ht0,1,2,3{p,q,r}		sr{p,q}	{p}×{}	{}×{r}	sr{q,r}

Cinco y más dimensiones

En cinco dimensiones y más, hay 3 politopos regulares, hipercubo, símplex y politopo de cruce. Son generalizaciones del cubo tridimensional, tetraedro y octaedro, respectivamente. No existen politopos estelares regulares en estas dimensiones. La mayoría de los politopos uniformes de dimensiones superiores se obtienen modificando los politopos regulares o tomando el producto cartesiano de politopos de dimensiones inferiores.

En seis, siete y ocho dimensiones entran en juego los exceptional simple Lie groups, E₆, E₇ y E₈. Al colocar anillos en un número distinto de cero de nodos de los Diagrama de Coxeter-Dynkin, se pueden obtener 39 nuevos 6 politopos, 127 nuevos 7 politopos y 255 nuevos 8 politopos. Un ejemplo notable es el 4₂₁ polytope.

Panales uniformes

Relacionados con el tema de los politopos uniformes finitos están los panales uniformes en espacios euclidianos e hiperbólicos. affine Coxeter groups genera panales uniformes euclidianos y hyperbolic Coxeter groups genera panales hiperbólicos. Se pueden multiplicar dos grupos de Coxeter afines.

Hay dos clases de grupos de Coxeter hiperbólicos, compactos y paracompactos. Los panales uniformes generados por grupos compactos tienen facetas y figuras de vértices finitas y existen en 2 a 4 dimensiones. Los grupos paracompactos tienen subgrafos afines o hiperbólicos y facetas infinitas o figuras de vértices, y existen en 2 a 10 dimensiones.

Véase también

• Símbolo de Schläfli

Referencias

• Coxeter La belleza de la geometría: doce ensayos, Publicaciones de Dover, 1999, ISBN 978-0-486-40919-1 (Capítulo 3: Construcción de Wythoff para politopos uniformes)
• Norman Johnson Politopos uniformes, Manuscrito (1991)
  • N.W. Johnson: La teoría de los politopos uniformes y los panales, Ph.D. Disertación, Universidad de Toronto, 1966
• A. Boole Stott: Deducción geométrica de politopos semirregulares a partir de regulares y rellenos espaciales, Verhandelingen de la unidad de ancho van Wetenschappen de la academia Koninklijke Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
• H.S.M. Coxeter:
  • H.S.M. Coxeter, M.S. Longuet-Higgins y J.C.P. Miller: Uniform Polyhedra, Philosophical Transactions of the Royal Society of London, Londres, 1954
  • H.S.M. Coxeter, Polytopes regulares, tercera edición, Dover, Nueva York, 1973
• Caleidoscopios: escritos seleccionados de H.S.M. Coxeter, editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
  • (Documento 22) H.S.M. Coxeter, Politopos regulares y semiregulares I, [Math. Tiempo. 46 (1940) 380-407, SEÑOR 2,10]
  • (Documento 23) H.S.M. Coxeter, Politopos regulares y semirregulares II, [Math. Tiempo. 188 (1985) 559-591]
  • (Documento 24) H.S.M. Coxeter, Politopos regulares y semirregulares III, [Math. Tiempo. 200 (1988) 3-45]
• Harold Scott MacDonald Coxeter, Longuet-Higgins, Miller, Poliedros uniformes, 'Phil. Trans. 1954, 246 A, 401-50. (Se utiliza la notación Schläfli extendida)
• Marco Möller, Vierdimensionale Archimedische Polytope, Disertación, Universität Hamburg, Hamburgo (2004) (en alemán)

Enlaces externos

• Plantilla:GlossaryForHyperspace
• politopos uniformes y convexos en cuatro dimensiones:, Marco Möller (en alemán)

• Datos: Q3887718