Pentadecágono
| Pentadecágono | ||
|---|---|---|
 Un pentadecágono regular | ||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 15 | |
| Vértices | 15 | |
| Grupo de simetría | , orden 2x15 | |
| Símbolo de Schläfli | {15} (pentadecágono regular) | |
| Diagrama de Coxeter-Dynkin |
| |
| Polígono dual | Autodual | |
| Área |
(lado ) | |
| Ángulo interior | 156° | |
| Propiedades | ||
| Convexo, isogonal, cíclico | ||
En geometría, un pentadecágono es un polígono de 15 lados y 15 vértices.[1]
Propiedades[editar]
Un pentadecágono tiene 90 diagonales, resultado que se puede obtener aplicando la ecuación general para determinar el número de diagonales de un polígono, ; siendo el número de lados , se tiene que:
La suma de todos los ángulos internos de cualquier pentadecágono es 2340 grados o radianes.
Pentadecágono regular[editar]

Un pentadecágono regular es el polígono que tiene todos sus lados de la misma longitud y todos sus ángulos internos iguales. Cada ángulo interno del pentadecágono regular mide 156º o rad. Cada ángulo externo del pentadecágono regular mide 24º o rad.
Al multiplicar la longitud t de un lado de un pentadecágono regular por quince (el número de lados n del polígono) obtendremos la longitud de su perímetro P.
El área A de un pentadecágono regular de lado t es de la siguiente forma:
donde es la constante pi y es la función tangente (con el argumento en radianes).
Si se conoce la longitud de la apotema a del polígono, otra alternativa para calcular el área es:
Construcción[editar]

- Construcciones de un pentadecágono
Como 15 = 3 × 5, un producto de distintos números de Fermat, un pentadecágono regular es construible usando regla y compás.
Las siguientes construcciones de pentadecágonos regulares con circuncírculo dado son similares a la ilustración de la proposición XVI en el Libro IV de los Elementos de Euclides.[2]
Compárese la construcción según Euclides en esta imagen: Pentadecágono
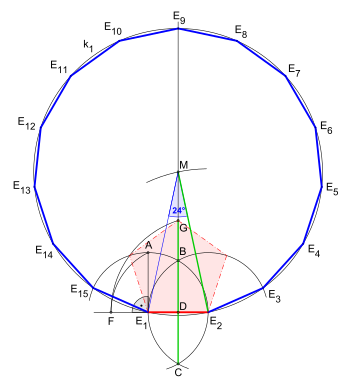
- Construcción de un pentadecágono inscrito en una circunferencia dada
En la construcción a partir de un círculo circunscrito dado: es un lado de un triángulo equilátero y es un lado de un pentágono regular.[3] El punto divide el radio según la relación del número áureo:
En comparación con la primera animación (con líneas verdes), en las dos imágenes siguientes se muestran los dos arcos circulares (para ángulos de 36° y 24°) rotados 90° en sentido antihorario. No utilizan el segmento , sino que utilizan el segmento como radio para el segundo arco circular (ángulo 36°).
- Construcción de un pentadecágono de lado conocido
Construcción de compás y regla para una longitud de lado determinada. La construcción es casi igual a la del pentágono de lado conocido. La presentación se logra mediante la extensión de un lado y se genera un segmento, aquí que se divide según la proporción áurea:
Circunradio Longitud lateral Ángulo
Simetría[editar]

El "pentadecágono regular" posee simetría diedral Dih15 de orden 30, representado por 15 ejes de simetría. El grupo Dih15 incluye 3 subgrupos diedrales: Dih5, Dih3 y Dih1, y cuatro simetrías cíclicas más: Z15, Z5, Z3 y Z1, con Zn representando la simetría rotacional de π/n radianes.En el pentadecágono se pueden dar 8 tipos de simetrías distintas.
John Conway clasificó estas simetrías usando una letra y el orden de la simetría a continuación. Asignó la letra r al grupo de simetría de la figura regular; y en el caso de los subgrupos utilizó la letra d (de diagonal) para las figuras con ejes de simetría solo a través de sus vértices; p para figuras con ejes de simetría solo a través de ejes perpendiculares a sus lados; i para figuras con ejes de simetría tanto a través de vértices como a través de centros de lados; y g para aquellas figuras solo con simetría rotacional. Con a1 se etiquetan aquellas figuras con ausencia de simetría.
Los tipos de simetrías más bajos permiten disponer de uno o más grados de libertad para definir distintas figuras irregulares.[4] Solo el subgrupo g15 no tiene grados de libertad, pero puede verse como un grafo dirigido. (Véase un ejemplo en la Teoría de grupos de John Conway)
Pentadecagramas[editar]
Hay tres estrellas regulares: {15/2}, {15/4} y {15/7}, construidas a partir de los mismos 15 vértices de un pentadecágono regular, pero conectados saltando cada segundo, cuarto o séptimo vértice respectivamente.
También hay otras tres estrellas regulares no continuas: {15/3}, {15/5} y {15/6}, la primera compuesta por tres pentágonos, la segunda por cinco triángulos equiláteros y la tercera formada por tres estrellas pentagonales .
La figura compuesta {15/3} puede verse vagamente como el equivalente bidimensional de una figura tridimensional, el compuesto de cinco tetraedros.
| Imagen |  {15/2} |
 {15/3} or 3{5} |
 {15/4} |
 {15/5} or 5{3} |
 {15/6} or 3{5/2} |
 {15/7} |
|---|---|---|---|---|---|---|
| Interior angle | 132° | 108° | 84° | 60° | 36° | 12° |
Los truncamientos más profundos del pentadecágono regular y los pentadecagramas pueden producir formas poligonales de estrellas intermedias isogonales (figura isogonal) con vértices espaciados iguales y dos longitudes de lado.[5]
| Truncamientos transitivos de vértice del pentadecágono | ||||||||
|---|---|---|---|---|---|---|---|---|
| Cuasirregular | Isogonal | Cuasirregular | ||||||
 t{15/2}={30/2} |

|

|

|

|

|

|

|
 t{15/13}={30/13} |
 t{15/7} = {30/7} |

|

|

|

|

|

|

|
 t{15/8}={30/8} |
 t{15/11}={30/22} |

|

|

|

|
|
|

|
 t{15/4}={30/4} |
Polígonos de Petrie[editar]
El pentadecágono regular es el polígono de Petrie para algunos politopos de mayor dimensión, mediante un operador de proyección oblicuo:
 Símplex (14D) |
Véase también[editar]
Referencias[editar]
- ↑ Real Academia Española. «Pentadecágono». Diccionario de la lengua española (23.ª edición). 1. adj. Geom. Dicho de un polígono: Que tiene quince ángulos y quince lados. U. m. c. s. m.
- ↑ Dunham, William (1991). Journey through Genius - The Great Theorems of Mathematics. Penguin. p. 65. Consultado el 12 de noviembre de 2015 – via the University of Kentucky College of Arts & Sciences Mathematics.
- ↑ Kepler, Johannes, translated and initiated by MAX CASPAR 1939. WELT-HARMONIK (en alemán). p. 44. Consultado el 7 de diciembre de 2015 – via Google Books. Retrieved on June 5, 2017
- ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
- ↑ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum
Enlaces externos[editar]
 Wikimedia Commons alberga una categoría multimedia sobre pentadecágonos.
Wikimedia Commons alberga una categoría multimedia sobre pentadecágonos.- Weisstein, Eric W. «Pentadecagon». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.