Prisma (geometría)
| Prisma | ||
|---|---|---|
 Imagen del sólido | ||
| Caras | n + 2 | |
| Polígonos que forman las caras |
2 n-ágonos n cuadrados | |
| Aristas | 3n | |
| Vértices | 2n | |
| Configuración de vértices | 4.4.n | |
| Grupo de simetría | Dnh | |
| Poliedro dual | Bipirámide n-gonal | |
| Símbolo de Schläfli |
{n}×{ } [1] t{2,n} | |
| Símbolo de Coxeter-Dynkin |
| |
| Conway | Pn | |
| Propiedades | ||
| Prismatoide | ||
| Desarrollo | ||
 | ||
Un prisma,[2] en geometría, es un poliedro que consta de dos caras iguales y paralelas llamadas bases, y de caras laterales que son paralelogramos. Los prismas se nombran por la forma de su base, por lo que un prisma de base pentagonal se llama prisma pentagonal.[3] Los prismas son una subclase de los prismatoides.[4]
Como muchos términos geométricos básicos, la palabra prisma (πρίσμα (prisma)|algo aserrado) se utilizó por primera vez en los Elementos de Euclides. Euclides definió el término en el Libro XI como "una figura sólida contenida por dos planos opuestos, iguales y paralelos, mientras que el resto son paralelogramos". Sin embargo, esta definición ha sido criticada por no ser lo suficientemente específica en relación con la naturaleza de las bases, lo que causó confusión entre los escritores de geometría posteriores.[5][6]
Definición[editar]
Un prisma es un poliedro que posee las siguientes dos propiedades:
- Existen exactamente dos caras congruentes sobre planos paralelos, que se denominan bases.
- Todas las demás caras son paralelogramos.[7]
Prisma regular[editar]
Un prisma regular es aquel cuyas bases son un polígono regular.
Prisma uniforme[editar]
Un prisma uniforme o prisma semirregular es un prisma recto con bases regulares y todas las aristas de la misma longitud.
Por tanto, todas las caras laterales de un prisma uniforme son cuadrados, y en consecuencia, todas sus caras son polígonos regulares. Además, dichos prismas son isogonales; y por lo tanto son poliedros uniformes. Forman una de las dos series infinitas de poliedros semirregulares, la otra serie está formada por los antiprismas.
Un prisma n-gonal uniforme tiene símbolo de Schläfli t{2,n}.
Oblicuo frente a recto[editar]

Un prisma oblicuo es un prisma en el que las aristas y caras de unión son no perpendiculares a las caras de la base.
Ejemplo: un paralelepípedo es un prisma oblicuo cuya base es un paralelogramo, o equivalentemente un poliedro con seis caras paralelogramos.
Un prisma recto es un prisma en el que las aristas y caras de unión son perpendiculares a las caras de la base.[8] Esto se aplica si y sólo si todas las caras de unión son rectangulares.[9]
El dual de un prisma recto n es una bipirámide recta n.
Un prisma recto (de lados rectangulares) con bases de polígono regular n-gon tiene símbolo de Schläfli { }×{n}. Se aproxima a un cilindro a medida que n se aproxima al infinito.[10]
Casos especiales[editar]
- Un prisma rectangular recto (con base rectangular) también se llama cuboide, o informalmente caja rectangular. Un prisma rectangular recto tiene símbolo de Schläfli { }×{ }×{ }.
- Un prisma cuadrado recto (con base cuadrada) también se denomina cuboide cuadrado, o informalmente caja cuadrada.
Nota: algunos textos pueden aplicar el término prisma rectangular o prisma cuadrado tanto a un prisma de base rectangular como a un prisma de base cuadrada.
Prismas rectos[editar]
Un prisma recto es un prisma en el que los bordes de unión y las caras son perpendiculares a las caras de la base. Esto se aplica si las caras de unión son rectangulares. Si los bordes de unión y las caras no son perpendiculares a las caras de la base, se llama prisma oblicuo.
Algunos textos pueden aplicar el término de prisma rectangular o prisma cuadrado tanto a un prisma rectangular de lado derecho como a un prisma unilateral cuadrado derecho. El término prisma uniforme puede utilizarse para un prisma recto con lados cuadrados, ya que tales prismas están en el conjunto de poliedros uniforme.
Un prisma de n caras laterales con extremos de polígonos regulares y caras rectangulares, se acerca un sólido cilíndrico cuando n tiende a infinito.
Los prismas rectos con bases regulares y longitudes iguales bordes forman una de las dos series infinitas de poliedros semirregulares, las otras series son los antiprismas.
El dual de un prisma recto es una bipirámide.
Un paralelepípedo es un prisma de que la base es un paralelogramo, o equivalentemente un poliedro con seis caras que son todas paralelogramos.
A un prisma rectangular recto también se lo conoce como cuboides, o informalmente caja rectangular. Un prisma cuadrado derecho es simplemente una caja cuadrada, y también puede ser llamado un cuboide cuadrado.Los prismas son poliedros que constan de dos caras iguales y paralelas llamadas bases, y de caras laterales que son paralelogramos.
Cada prisma consta de los siguientes elementos:
- Bases: son las dos caras iguales y paralelas del prisma, una en la que se apoya y la otra su opuesta.
- Caras laterales: son las caras que comparten dos de sus lados con las bases. La suma de sus áreas es la superficie lateral del prisma.
- Aristas: son los lados de las bases y de las caras laterales.
- Vértices: son los puntos en donde se encuentran cada par de aristas.
- Altura: es la distancia entre las bases.
- Diagonales: son los segmentos que unen dos vértices no consecutivos del prisma. Se pueden trazar las diagonales de una cara o entre dos caras.
Superficie[editar]
El área superficial de un prisma recto es:
donde B es el área de la base, h la altura, y P el perímetro de la base.
La superficie de un prisma recto cuya base es un polígono regular de lados n, de longitud s y altura h, es por tanto:
Volumen[editar]
El volumen de un prisma es el producto del área de la base por la distancia o altura entre las dos bases. Su valor se expresa como:
donde B es el área de la base y h es la altura. El volumen de un prisma, cuya base es un polígono regular de n lados con una longitud de lado s, es:
Diagramas de Schlegel[editar]
 P3 |
 P4 |
 P5 |
 P6 |
 P7 |
 P8 |
Simetría[editar]
El grupo de simetría de un prisma recto de n lados con la base regular es Dnh de orden 4n, excepto en el caso de un cubo, que tiene el grupo de simetría octaédrica más grande, de orden 48, que tiene como subgrupos tres versiones de D4h. El grupo de rotación es Dn de orden 2n, excepto en el caso de un cubo, que tiene el grupo O de simetría más grande de orden 24, que a su vez tiene como subgrupos tres versiones de D4.
El grupo de simetría Dnh posee simetría central si y solo si n es par.
Prisma truncado[editar]

Un prisma truncado o tronco de prisma es una parte de un prisma limitada entre la base y la sección originada por un plano no paralelo a la base, y que interseca a todas las aristas laterales.[11] Las bases del prisma una vez truncado no son congruentes entre sí y sus lados no son paralelogramos. [12]
Prisma torcido[editar]
Un prisma torcido es un poliedro no convexo construido a partir de un prisma uniforme de n lados con cada cara lateral dividida en dos triángulos según una diagonal, girando la parte superior generalmente en Πn radianes (180n grados), haciendo que los lados resultantes formen intersecciones cóncavas.[13][14]
Esta forma no puede diseccionarse en tetraedros sin agregar nuevos vértices. El caso más pequeño, con base triangular, se denomina poliedro de Schönhardt.
Un prisma torcido n-gonal es topológicamente idéntico a un antiprisma n-gonal uniforme, pero solo posee la mitad de su grupo de simetría: Dn, [n,2]+, de orden 2 n. Puede verse como un antiprisma no convexo, con tetraedros eliminados entre pares de triángulos.
| 3-gonal | 4-gonal | 12-gonal | |
|---|---|---|---|
 Poliedro de Schönhardt |
 Prisma cuadrado torcido |
 Antiprisma cuadrado |
 Prisma dodecagonal torcido |
Tronco[editar]
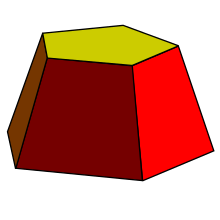
Un tronco es una construcción similar a un prisma, pero con las caras laterales trapeciales y los polígonos superior e inferior de diferentes tamaños.
Prisma en estrella[editar]
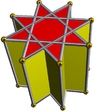
Un prisma en estrella es un poliedro no convexo construido por dos caras con forma de estrella idénticas en la parte superior e inferior, paralelas y desplazadas una distancia entre sí y conectadas por caras rectangulares. Un prisma en estrella uniforme tendrá Símbolo de Schläfli {p/q} × { }, con p rectángulos y 2 {p/q} caras. Es topológicamente idéntico a un prisma p-gonal.
| {}×{}180×{} | ta{3}×{} | {5/2}×{} | {7/2}×{} | {7/3}×{} | {8/3}×{} | |
|---|---|---|---|---|---|---|
| D2h, orden 8 | D3h, orden 12 | D5h, orden 20 | D7h, orden 28 | D8h, orden 32 | ||

|

|

|

|

|

|
|
Prisma cruzado[editar]
Un prisma cruzado es un poliedro no convexo construido a partir de un prisma, donde los vértices de una base son invertidos alrededor del centro de esta base (o girados 180°). Esto transforma las caras rectangulares laterales en rectángulos cruzados]. Para una base de polígono regular, la apariencia es la de un reloj de arena n-gonal. Todas las aristas oblicuas pasan por un único punto, el centro del cuerpo. Nota: no hay ningún vértice en este centro del cuerpo. Un prisma cruzado es topológicamente idéntico a un prisma n-gonal.
| {}×{}180×{}180 | ta{3}×{}180 | {3}×{}180 | {4}×{}180 | {5}×{}180 | {5/2}×{}180 | {6}×{}180 | |
|---|---|---|---|---|---|---|---|
| D2h, orden 8 | D3d, orden 12 | D4h, orden 16 | D5d, orden 20 | D6d, orden 24 | |||

|

|

|

|

|

|

|

|
Prisma toroidal[editar]
Un prisma toroidal es un poliedro no convexo como un prisma cruzado, pero sin caras de base superior e inferior, y con caras laterales rectangulares simples que cierran el poliedro. Esto solo se puede hacer cuando las bases son polígonos con un número par de lados. Topológicamente son toros, con característica de Euler cero. Su desarrollo se puede generar a partir de dos filas de un teselado cuadrado (con configuración de vértices 4.4.4.4): una banda de n cuadrados, cada uno unido a un rectángulo cruzado. Un prisma toroidal n-gonal tiene 2n vértices, 2n caras (n cuadrados y n rectángulos cruzados), y 4n aristas. Es topológicamente autodual.
| D4h, orden 16 | D6h, orden 24 |
| v=8, e=16, f=8 | v=12, e=24, f=12 |

|

|
Politopo prismático[editar]
Un politopo prismático es una generalización de los prismas a dimensiones distintas de 3. Un polítopo prismático de n dimensiones se define recursivamente como una figura creada a partir de dos politopos congruentes (n − 1)-dimensionales en hiperplanos paralelos, cuyas facetas correspondientes se conectan por prismas (n − 1)-dimensionales.
Dado un n-politopo con fi elementos de dimensión i (i = 0, ..., n), el prisma generado a partir de él tendrá 2fi + fi−1 elementos de dimensión i (tomando f−1 = 0, fn = 1).
Por dimensión:
- Si se parte de un polígono con n vértices y n aristas, su prisma tendrá 2n vértices, 3n aristas y 2 + n caras.
- Si se parte de un poliedro con v vértices, e aristas y f caras, su prisma tendrá 2v vértices, 2e + v aristas, 2f + e caras, y 2 + f celdas.
- Si se parte de un polícoro con v vértices, e aristas, f caras y c celdas, su prisma tendrá 2v vértices, 2e + v aristas, 2f + e caras, y 2 + c hiperceldas.
Politopo prismático uniforme[editar]
Un n-polítopo regular de representado por el símbolo de Schläfli {p, q, ..., t} puede formar un (n + 1)-polítopo prismático uniforme representado por un producto cartesiano de dos símbolos de Schläfli: {p, q, ..., t} × {}.
Por dimensión:
- Un prisma 0-politópico es un segmento de recta, representado por un símbolo de Schläfli vacío {}.
- Un prisma 1-politópico es un rectángulo, formado a partir de la traslación de 2 segmentos de línea. Se representa como los el símbolo Schläfli producto {} × {}. Si se trata de un cuadrado, se puede reducir la simetría a: {} x {} = {4}.
- Un prisma poligonal es un prisma de 3 dimensiones hecho a partir de dos polígonos trasladados, conectados por rectángulos. Un polígono regular {p} puede construir el prisma n-gonal uniforme representado por el producto {p} × {}. Si p = 4, con lados cuadrados simétricos, se convierte en un cubo: {4}×{} = {4, 3}.
 Ejemplo: prisma pentagonal, {5}×{}, dos pentágonos paralelos conectados por 5 lados rectangulares.
Ejemplo: prisma pentagonal, {5}×{}, dos pentágonos paralelos conectados por 5 lados rectangulares.
- Un prisma poliédrico es un prisma de 4 dimensiones hecho por dos poliedros trasladados conectados por celdas de prisma de tridimensionales. Un poliedro regular {p, q} puede construir el prisma policórico uniforme, representado por el producto {p, q}×{}. Si el poliedro es un cubo, y los lados son cubos, se convierte en un teseracto: {4, 3}×{} = {4, 3, 3}.
 Ejemplo: prisma dodecaédrico {5, 3} × {}, dos dodecaedros paralelos conectados por 12 lados de prismas pentagonales.
Ejemplo: prisma dodecaédrico {5, 3} × {}, dos dodecaedros paralelos conectados por 12 lados de prismas pentagonales.

Los politopos prismáticos de orden superior también existen como producto cartesiano de dos o más politopos cualesquiera. La dimensión de un politopo de producto es la suma de las dimensiones de sus elementos. Los primeros ejemplos de estos existen en el espacio de 4 dimensiones; se llaman duoprisma como el producto de dos polígonos en 4 dimensiones.
Los duoprismas regulares se representan como {p}×{q}, con vértices pq, aristas de 2pq, caras cuadradas pq, p Caras q-gon, caras q'p-gon y delimitadas por prismas p'q-gonal y q p -prismas diagonales.
Por ejemplo, {4}×{4}, un duoprisma 4-4 es una forma de simetría inferior de un teseracto, al igual que {4,3}×{ }, un prisma cúbico. {4}×{4}×{ } (prisma de duoprisma 4-4), {4,3}×{4} (duoprisma de cubo-4) y {4,3,3}×{ } (prisma teseractico prisma) son formas de simetría inferior de un penteracto.
| Simetría | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|
| Imagen | 
|

|

|

|

|

|

|

|
Véase también[editar]
Referencias[editar]
- ↑ Johnson, N. W (2018). «Chapter 11: Finite symmetry groups». Geometries and Transformations. ISBN 978-1-107-10340-5. See 11.3 Pyramids, Prisms, and Antiprisms, Figure 11.3b.
- ↑ Real Academia Española. «prisma». Diccionario de la lengua española (23.ª edición). (Del lat. tardío prisma, y este del gr. πρῖσμα prîsma.) prisma: 1. m. Geom. Cuerpo limitado por dos polígonos planos, paralelos e iguales, que se llaman bases, y por tantos paralelogramos cuantos lados tengan dichas bases, las cuales, según su forma, dan nombre al prisma: triangular, pentagonal, etc.
- ↑ Wellman, B. Leighton (1976). Geometría descriptiva: compendio de geometría descriptiva para técnicos. Reverte. ISBN 978-84-291-5090-2. Consultado el 29 de noviembre de 2019.
- ↑ Grünbaum, Branko (1997). «Isogonal Prismatoids». Discrete & Computational Geometry 18: 13-52. doi:10.1007/PL00009307.
- ↑ Thomas Malton (1774). A Royal Road to Geometry: Or, an Easy and Familiar Introduction to the Mathematics. ... Por Thomas Malton. .... autor, and sold. pp. 360-.
- ↑ James Elliot (1845). Clave para el tratado completo de geometría práctica y mensuración: Containing Full Demonstrations of the Rules .... Longman, Brown, Green, and Longmans. pp. 3-.
- ↑ Stanley R. Clemens Geometría con aplicaciones y solución de problemas. Addison - Wesley Iberoamericana. Wilmington, Delaware E.U.A. (1989)
- ↑ William F. Kern, James R. Bland, Solid Mensuration with proofs, 1938, p. 28.
- ↑ Kern, William F.; Bland, James R. (1938). Solid Mensuration with proofs. pp. 28.
- ↑ Geretschlager, Robert (2020). Engaging Young Students In Mathematics Through Competitions: World Perspectives And Practices 1. World Scientific. p. 39. ISBN 978-981-120-582-8.
- ↑ Eitor general Raúl Moisés Izaguirre Maguiña Geometría Fondo Editorial UNMSM -Centro preuniversitario Lima (2011) 3º edición
- ↑ Kern y Bland, 1938, p. 81.
- ↑ Gorini, Catherine A. (2003). The facts on file: Geometry handbook. p. 172. ISBN 0-8160-4875-4.
- ↑ «Pictures of Twisted Prisms».
Bibliografía[editar]
- Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 2: Archimedean polyhedra, prisma and antiprisms
Enlaces externos[editar]
- Olshevsky, George, Prismatic polytope en Glossary for Hyperspace (en inglés)
- Prismas y antiprismas no convexos (en inglés)
- Área de la superficie en MATHguide (en inglés)
- Volumen en MATHguide (en inglés)
- Modelos de papel de prismas y antiprismas. Redes libres de prismas y antiprismas (en inglés).
- Modelos de papel de prismas y antiprismas usando redes generadas por Stella (en inglés)
- Stella: Navigador Poliedro: Software utilizado para crear las imágenes 3D y 4D en esta página (en inglés).







