Lógica

La lógica es una rama de la filosofía[1][2][3][4][5] de carácter interdisciplinario, entendida como la ciencia formal que estudia los principios de la demostración y la inferencia válida,[6] las falacias, las paradojas y la noción de verdad.[7]
La lógica se divide en varias categorías según su campo de estudio. La lógica filosófica estudia el concepto y la definición, la enunciación o proposición y la argumentación utilizando los métodos y resultados de la lógica moderna para el estudio de problemas filosóficos. La lógica matemática estudia la inferencia mediante sistemas formales como la lógica proposicional, la lógica de primer orden y la lógica modal. La lógica informal se enfoca en el desarrollo lingüístico de los razonamientos y sus falacias. La lógica computacional es la aplicación de la lógica matemática a las ciencias de la computación.
Los orígenes de la lógica se remontan a la Edad Antigua, con brotes independientes en China, India y Grecia. Desde entonces, la lógica tradicionalmente se considera una rama de la filosofía, pero en el siglo XX la lógica ha pasado a ser principalmente la lógica matemática, y por lo tanto ahora también se considera parte de las matemáticas, e incluso una ciencia formal independiente.
No existe un acuerdo universal sobre la definición exacta o los límites de la lógica.[8][9][10] Sin embargo, el ámbito de la lógica (interpretada en sentido amplio) incluye:
- La clasificación de los argumentos.
- El análisis sistemático de las formas lógicas.
- El estudio sistemático de la validez de las inferencias deductivas.
- La fuerza de las inferencias inductivas.
- El estudio de los argumentos defectuosos, como las falacias.
- El estudio de las paradojas lógicas.
- El estudio de la sintaxis y la semántica de los lenguajes formales.
- El estudio de los conceptos de sentido, denotación y verdad.
Históricamente, la lógica se ha estudiado principalmente en filosofía desde la antigüedad, en matemáticas desde mediados del siglo XIX y en informática desde mediados del siglo XX. Más recientemente, la lógica también se ha estudiado en lingüística y en ciencias cognitivas. En general, la lógica sigue siendo un área de estudio fuertemente interdisciplinaria.
Etimología y acepciones[editar]
La palabra «lógica» deriva del griego antiguo λογική logikḗ, que significa «dotada de razón, intelectual, dialéctica, argumentativa» y que a su vez viene de λόγος (lógos), «palabra, pensamiento, idea, argumento, razón o principio».[11][12][i]
En el lenguaje cotidiano, expresiones como «lógica» o «pensamiento lógico» aportan también un sentido alrededor de un «pensamiento lateral» comparado, haciendo los contenidos de la afirmación coherentes con un contexto, bien sea del discurso o de una teoría de la ciencia, o simplemente con las creencias o evidencias transmitidas por la tradición cultural.
Del mismo modo existe el concepto sociológico y cultural de lógica como por ejemplo «lógica deportiva», que en general, podríamos considerar como «lógica cotidiana» - también conocida como «lógica del sentido común».
En estas áreas la «lógica» suele tener una referencia lingüística en la pragmática.
Un argumento en este sentido tiene su «lógica» cuando resulta convincente, razonable y claro; en definitiva cuando cumple una función de eficacia. La habilidad de pensar y expresar un argumento así corresponde a la retórica, cuya relación con la verdad es una relación probable.
Temas[editar]
Inferencia[editar]
La inferencia es el proceso por el cual se derivan conclusiones a partir de premisas o hipótesis iniciales.[13] Cuando una conclusión se sigue de sus premisas o hipótesis de partida, por medio de deducciones lógicas válidas, se dice que las premisas implican (infieren) la conclusión.
La inferencia es el objeto de estudio tradicional de la lógica, así como la vida es el objeto de estudio de la biología. La lógica investiga los fundamentos por los cuales algunas inferencias son aceptables, y otras no. Cuando una inferencia es aceptable, lo es por su estructura lógica y no por el contenido específico del argumento o el lenguaje utilizado (retórica). Por esto se construyen sistemas lógicos que capturan los factores relevantes de las deducciones que aparecen en el lenguaje natural.[14]
Tradicionalmente, se distinguen tres clases de inferencias: las deducciones, las inducciones y las abducciones, aunque a veces se cuenta a la abducción como un caso especial de inducción.[15] Las inducciones se estudian desde la lógica inductiva y el problema de la inducción. Las deducciones, en cambio, son estudiadas por la mayor parte de la lógica contemporánea.[16]
En las investigaciones sobre la inteligencia artificial, la inferencia es la operación lógica utilizada en los motores de inferencia de los sistemas expertos.[cita requerida]Validez[editar]
En lógica, la validez es una propiedad que tienen los argumentos cuando las premisas implican la conclusión. Si la conclusión es una consecuencia lógica de las premisas, se dice que el argumento es deductivamente válido.[17] Algunos consideran estas dos nociones idénticas y usan ambos términos indistintamente. Otros, sin embargo, consideran que puede haber argumentos que no sean deductivamente válidos, como las inducciones. En cualquier caso, de las inducciones a veces se dice que son buenas o malas, en vez de válidas o inválidas.
Ejemplos de argumentos deductivamente válidos son los siguientes:
|
|
|
Para que un argumento sea lo que le da principalmente la validez a un argumento es la seguridad con lo que lo dice la persona y que tenga razón con lo que dice deductivamente válido, no es necesario que las premisas o la conclusión sean verdaderas. Sólo se requiere que la conclusión sea una consecuencia lógica de las premisas. La lógica formal exige únicamente una relación condicional entre las premisas y la conclusión. Esto es: que si las premisas son verdaderas, entonces la conclusión también lo es (esta es la caracterización semántica de la noción de consecuencia lógica); o alternativamente: que la conclusión sea deducible de las premisas conforme a las reglas de un sistema lógico (esta es la caracterización sintáctica de la noción de consecuencia lógica). Si un argumento, además de ser válido, tiene premisas verdaderas, entonces se dice que es sólido.
Las expresiones de las que depende la validez de los argumentos se llaman constantes lógicas, y la lógica las estudia mediante sistemas formales.[18]Falacias[editar]
En lógica, una falacia (del latín fallacia ‘engaño’) es un argumento que parece válido, pero no lo es.[19][20] Algunas falacias se cometen intencionadamente para persuadir o manipular a los demás, mientras que otras se cometen sin intención debido a descuidos o ignorancia. En ocasiones las falacias pueden ser muy sutiles y persuasivas, por lo que se debe poner mucha atención para detectarlas.[21]
Que un argumento sea falaz no implica que sus premisas o su conclusión sean falsas ni que sean verdaderas. Un argumento puede tener premisas y conclusión verdaderas y aun así ser falaz. Lo que hace falaz a un argumento es la invalidez del argumento en sí. De hecho, inferir que una proposición es falsa porque el argumento que la contiene por conclusión es falaz es en sí una falacia conocida como argumento ad logicam.[22]
El estudio de las falacias se remonta por lo menos hasta Aristóteles, quien en sus Refutaciones sofísticas identificó y clasificó trece clases de falacias.[19] Desde entonces se han agregado a la lista cientos de otras falacias y se han propuesto varios sistemas de clasificación.[23]
Las falacias son de interés no solo para la lógica, sino también para la política, la retórica, el derecho, la ciencia, la religión, el periodismo, la mercadotecnia, el cine y, en general, cualquier área en la cual la argumentación y la persuasión sean de especial relevancia.Paradojas[editar]

Verdad[editar]


El uso de la palabra verdad abarca asimismo la honestidad, la buena fe y la sinceridad humana en general; también el acuerdo de los conocimientos con las cosas que se afirman como realidades: los hechos o la cosa en particular;[29] y, finalmente, la relación de los hechos o las cosas en su totalidad en la constitución del Todo, el Universo.[30]
Las cosas son verdaderas cuando son «fiables», cuando cumplen lo que ofrecen.[31][32]
El término no tiene una única definición en la que estén de acuerdo la mayoría de los estudiosos y las teorías sobre la verdad continúan siendo ampliamente debatidas. Hay posiciones diferentes acerca de cuestiones como:
- Qué es lo que constituye la verdad.
- Con qué criterio podemos identificarla y definirla.
- Si el ser humano posee conocimientos innatos o solo puede adquirirlos.
- Si existen las revelaciones o la verdad puede alcanzarse tan solo mediante la experiencia, el entendimiento y la razón.
- Si la verdad es subjetiva u objetiva.
- Si la verdad es relativa o absoluta.
- Y hasta qué grado pueden afirmarse cada una de dichas propiedades.
Este artículo procura introducir las principales interpretaciones y perspectivas, tanto históricas como actuales, acerca de este concepto.
La pregunta por la verdad es y ha sido objeto de debate entre teólogos, filósofos y lógicos a lo largo de los siglos considerándose un tema concerniente al alma y al estudio de una llamada psicología racional dentro del campo de la filosofía.
En la actualidad es un tema de investigación científica así como de fundamentación filosófica:[33]
- La investigación científica de la función cognitiva[34] introduce nuevas perspectivas acerca del conocimiento basado en la evidencia como creencia epistemológicamente verdadera con justificación válida.[35]
- Interesa a la lingüística pues el lenguaje es expresión de la propia verdad.
- Interesa a la antropología filosófica, pues parece evidente que los seres humanos prefieren la verdad a la falsedad, al error o la mentira y prefieren la certeza a la duda.
- Interesa a la historia, por cuanto el aprecio hacia la verdad y la condena de la mentira o del error varía en intensidad según las épocas y las culturas, pues tanto el concepto de verdad como su valoración no siempre es el mismo a lo largo de la historia y según las diferentes culturas.
- Interesa a la ciencia en cuanto tal[36] en su pretensión de conocimiento válido.
Ramas[editar]
Sobre esta primera, y en cierto sentido única, regla de la razón, de que para aprender hay que desear aprender, y al desearlo no conformarse con lo que ya se inclina a pensar de forma capaz, se desprende un corolario que merece por sí mismo ser inscrito en cada muro de la ciudad de la filosofía: No bloquees el camino de la investigación. —Charles Sanders Peirce, Primera regla de la lógica
|
Lógica matemática[editar]
La lógica matemática, también llamada lógica simbólica, lógica teorética, lógica formal o logística,[37] es el estudio formal y simbólico de la lógica, y su aplicación a algunas áreas de la matemática y la ciencia. Comprende la aplicación de las técnicas de la lógica formal a la construcción y el desarrollo de las matemáticas y el razonamiento matemático, y conversamente la aplicación de técnicas matemáticas a la representación y el análisis de la lógica formal. La investigación en lógica matemática ha jugado un papel crucial en el estudio de los fundamentos de las matemáticas.
La lógica matemática estudia la inferencia mediante la construcción de sistemas formales como la lógica proposicional, la lógica de primer orden o la lógica modal. Estos sistemas capturan las características esenciales de las inferencias válidas en los lenguajes naturales, pero al ser estructuras formales susceptibles de análisis matemático, permiten realizar demostraciones rigurosas sobre ellas.
La lógica matemática se suele dividir en cuatro áreas: teoría de modelos, teoría de la demostración, teoría de conjuntos y teoría de la computabilidad. La teoría de la demostración y la teoría de modelos fueron el fundamento de la lógica matemática. La teoría de conjuntos se originó en el estudio del infinito por Georg Cantor y ha sido la fuente de muchos de los temas más desafiantes e importantes de la lógica matemática, desde el teorema de Cantor, el axioma de elección y la cuestión de la independencia de la hipótesis del continuo, al debate moderno sobre grandes axiomas cardinales. La lógica matemática tiene estrechas conexiones con las ciencias de la computación. La teoría de la computabilidad captura la idea de la computación en términos lógicos y aritméticos. Sus logros más clásicos son la indecidibilidad del Entscheidungsproblem de Alan Turing y su presentación de la tesis de Church-Turing. Hoy en día, la teoría de la computabilidad se ocupa principalmente del problema más refinado de las clases de complejidad (¿cuándo es un problema eficientemente solucionable?) y de la clasificación de los grados de insolubilidad.
La lógica matemática también estudia las definiciones de nociones y objetos matemáticos básicos como conjuntos, números, demostraciones y algoritmos. La lógica matemática estudia las reglas de deducción formales, las capacidades expresivas de los diferentes lenguajes formales y las propiedades metalógicas de los mismos.
En un nivel elemental, la lógica proporciona reglas y técnicas para determinar si es o no válido un argumento dado dentro de un determinado sistema formal. En un nivel avanzado, la lógica matemática se ocupa de la posibilidad de axiomatizar las teorías matemáticas, de clasificar su capacidad expresiva, y desarrollar métodos computacionales útiles en sistemas formales. La teoría de la demostración y la matemática inversa son dos de los razonamientos más recientes de la lógica matemática abstracta. Debe señalarse que la lógica matemática se ocupa de sistemas formales que pueden no ser equivalentes en todos sus aspectos, por lo que la lógica matemática no es un método para descubrir verdades del mundo físico real, sino solo una fuente posible de modelos lógicos aplicables a teorías científicas, muy especialmente a la matemática convencional.
Por otra parte, la lógica matemática no estudia el concepto de razonamiento humano general o el proceso creativo de construcción de demostraciones matemáticas mediante argumentos rigurosos pero con lenguaje informal con algunos signos o diagramas, sino solo de demostraciones y razonamientos que se pueden formalizar por completo.Lógica computacional[editar]
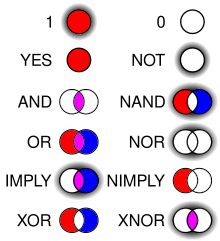
La lógica computacional es la misma lógica matemática aplicada al contexto de las ciencias de la computación. Su uso es fundamental en varios niveles: en los circuitos computacionales, en la programación lógica y en el análisis y optimización (de recursos temporales y espaciales) de algoritmos.
La lógica se extiende al corazón de la informática a medida que surge como una disciplina: El trabajo de Alan Turing sobre el Entscheidungsproblem seguido del trabajo de Kurt Gödel sobre teoremas incompletos. La noción de la computadora de uso general que surgió de este trabajo fue de gran importancia para los diseñadores de la maquinaria informática en la década de 1940.
En los años 50 y 60, investigaciones predijeron que, cuando el conocimiento humano se pudiera expresar usando la lógica con notaciones matemáticas, sería posible crear una máquina capaz de razonar o una inteligencia artificial. Esto fue más difícil de lo esperado a causa de la complejidad del razonamiento humano. En la lógica de programación, un programa consiste en una colección de axiomas y reglas. Los sistemas de programación lógicos (como Prolog) calculan las consecuencias de los axiomas y las reglas organizadas para responder a una consulta.
Hoy en día, la lógica es extensamente aplicada en los campos de inteligencia artificial y de ciencias de computación, y estos campos proporcionan una rica fuente de problemas en la lógica formal e informal. La teoría de la argumentación es un buen ejemplo de cómo la lógica está siendo aplicada a la inteligencia artificial. El sistema de clasificación computacional ACM, en particular, considera:
- Sección F.3 en Lógicas y significados de programas y F.4 en Lógica matemática y lenguajes formales como parte de la teoría de la ciencia de computación: este trabajo cubre la semántica formal de los lenguajes de programación tan bien como el trabajo de métodos formales como la lógica de Hoare.
- Lógica booleana como fundamento en el hardware de la computadora, particularmente la sección del sistema B.2 en la estructura aritmética y lógica, relacionado con operadores AND, NOT y OR.
- Muchos formalismos lógicos fundamentales son esenciales para la sección I.2 sobre inteligencia artificial, por ejemplo la lógica modal y la lógica por defecto en los formalismos y métodos de representación del conocimiento, las cláusulas de Horn en la programación lógica y la lógica de descripción.
Lógica filosófica[editar]
Entendida en un sentido estricto, la lógica filosófica es el área de la filosofía que estudia la aplicación de métodos lógicos a problemas filosóficos, a menudo en forma de sistemas lógicos extendidos como la lógica modal. Algunos teóricos conciben la lógica filosófica en un sentido más amplio como el estudio del alcance y la naturaleza de la lógica en general. En este sentido, la lógica filosófica puede considerarse idéntica a la filosofía de la lógica, que incluye temas adicionales como la definición de la lógica o la discusión de los conceptos fundamentales de la lógica. El presente artículo trata la lógica filosófica en el sentido estricto, en el que constituye un campo de investigación dentro de la filosofía de la lógica.
Un tema importante para la lógica filosófica es la cuestión de cómo clasificar la gran variedad de sistemas lógicos no clásicos, muchos de los cuales son de origen bastante reciente. Una forma de clasificación que se encuentra a menudo en la literatura es distinguir entre lógicas extendidas y lógicas desviadas. La lógica misma puede definirse como el estudio de la inferencia válida. La lógica clásica es la forma dominante de la lógica y articula reglas de inferencia de acuerdo con intuiciones lógicas compartidas por muchos, como el principio del tercero excluido, la eliminación de la doble negación y la bivalencia de la verdad.
Las lógicas extendidas son sistemas lógicos que se basan en la lógica clásica y sus reglas de inferencia, pero la extienden a nuevos campos introduciendo nuevos símbolos lógicos y las correspondientes reglas de inferencia que rigen estos símbolos. En el caso de la lógica modal alética, estos nuevos símbolos se utilizan para expresar no solo lo que es verdadero simpliciter, sino también lo que es posible o necesariamente verdadero. A menudo se combina con la semántica de los mundos posibles, que sostiene que una proposición es posiblemente verdadera si es verdadera en algún mundo posible, mientras que es necesariamente verdadera si es verdadera en todos los mundos posibles. La lógica deóntica pertenece a la ética y proporciona un tratamiento formal de las nociones éticas, como la obligación y el permiso. La lógica temporal formaliza las relaciones temporales entre proposiciones. Esto incluye ideas como si algo es verdadero en algún momento o todo el tiempo y si es verdadero en el futuro o en el pasado. La lógica epistémica pertenece a la epistemología. Puede usarse para expresar no solo lo que es el caso, sino también lo que alguien cree o sabe que es el caso. Sus reglas de inferencia articulan lo que se desprende del hecho de que alguien tiene estos tipos de estados mentales. Las lógicas de orden superior no aplican directamente la lógica clásica a ciertos subcampos nuevos dentro de la filosofía, sino que la generalizan al permitir la cuantificación no solo sobre individuos sino también sobre predicados.
Las lógicas desviadas, en contraste con estas formas de lógicas extendidas, rechazan algunos de los principios fundamentales de la lógica clásica y a menudo son vistas como sus rivales. La lógica intuicionista se basa en la idea de que la verdad depende de la verificación a través de una prueba. Esto la lleva a rechazar ciertas reglas de inferencia encontradas en la lógica clásica que no son compatibles con esta suposición. La lógica libre modifica la lógica clásica para evitar los presupuestos existenciales asociados al uso de términos singulares posiblemente vacíos, como nombres y descripciones definidas. Las lógicas plurivalentes permiten valores de verdad adicionales además de verdadero y falso. Por lo tanto, rechazan el principio de bivalencia de la verdad. Las lógicas paraconsistentes son sistemas lógicos capaces de lidiar con contradicciones. Lo hacen evitando el principio de explosión que se encuentra en la lógica clásica. La lógica relevante es una forma prominente de lógica paraconsistente. Rechaza la interpretación puramente funcional de verdad del condicional material al introducir el requisito adicional de relevancia: para que el condicional sea verdadero, su antecedente tiene que ser relevante para su consecuente.Lógica informal[editar]
Lógica silogística[editar]

El Organon fue el conjunto de trabajos de Aristóteles sobre lógica, constituyendo los Primeros analíticos el primer trabajo explícito de lógica formal, introduciendo la silogística.[38] Las partes de la lógica silogística, también conocida con el nombre de lógica de términos, son el análisis de los juicios en proposiciones que consisten en dos términos que están relacionados por una de un número fijo de relaciones, y la expresión de inferencias mediante silogismos que consisten en dos proposiciones que comparten un término común como premisa, y una conclusión que es una proposición que involucra los dos términos no relacionados de las premisas.
La obra de Aristóteles fue considerada en la época clásica y a partir de la época medieval en Europa y Oriente Medio como la imagen misma de un sistema totalmente elaborado. Sin embargo, no fue el único: los estoicos propusieron un sistema de lógica proposicional que fue estudiado por los lógicos medievales. También el problema de la generalidad múltiple fue reconocido en la época medieval. No obstante, no se consideraba que los problemas de la lógica silogística necesitaran soluciones revolucionarias.
Hoy en día, algunos académicos afirman que el sistema de Aristóteles es generalmente visto como algo que tiene poco más que valor histórico (aunque hay algún interés actual en la ampliación de la lógica de términos), considerado como obsoleto por el advenimiento de la lógica proposicional y el cálculo de predicados. Otros utilizan a Aristóteles en la teoría de la argumentación para ayudar a desarrollar y cuestionar críticamente los «esquemas de argumentación» que se utilizan en la inteligencia artificial y en los argumentos legales.
Lógica proposicional[editar]
Un cálculo o lógica proposicional (también un cálculo sentencial) es un sistema formal en el que las fórmulas que representan proposiciones pueden formarse combinando proposiciones atómicas (normalmente representadas con p, q, etc.) utilizando conectivos lógicos ( etc.); estas proposiciones y conectivas son los únicos elementos de un cálculo proposicional estándar.[39] A diferencia de la lógica de predicados o la lógica silogística, donde los sujetos y predicados individuales (que no tienen valores de verdad) son la unidad más pequeña, la lógica proposicional toma proposiciones completas con valores de verdad como su componente más básico.[39] Los cuantificadores (por ejemplo, o ) se incluyen en el cálculo proposicional extendido, pero solo cuantifican sobre proposiciones completas, no sobre sujetos o predicados individuales.[39] Una lógica proposicional dada es un sistema de prueba formal con reglas que establecen qué fórmulas bien formadas de un lenguaje dado son "teoremas" demostrándolos a partir de axiomas que se asumen sin prueba.[40]
Lógica modal[editar]
En el lenguaje, la modalidad se ocupa del fenómeno de que las subpartes de una oración pueden tener su semántica modificada por verbos especiales o partículas modales. Por ejemplo, "Vamos a los juegos puede modificarse para dar "Debemos ir a los juegos', y "Podemos ir a los juegos y quizás "Iremos a los juegos. De forma más abstracta, podríamos decir que la modalidad afecta a las circunstancias en las que damos por satisfecha una afirmación. La confusión de la modalidad se conoce como falacia modal.
La lógica de Aristóteles se ocupa en gran parte de la teoría de la lógica no modalizada. Aunque, hay pasajes en su obra, como el famoso argumento de la batalla naval en Sobre la interpretación § 9, que ahora se ven como anticipaciones de la lógica modal y su conexión con la potencialidad y el tiempo, el primer sistema formal de lógica modal fue desarrollado por Avicena, que finalmente desarrolló una teoría de la "temporal modalizada" silogística.[41]
Aunque el estudio de la necesidad y la posibilidad siguió siendo importante para los filósofos, apenas se produjeron innovaciones lógicas hasta las históricas investigaciones de C. I. Lewis en 1918, quien formuló una familia de axiomatizaciones rivales de la modalidades aleatorias. Su trabajo desató un torrente de nuevos trabajos sobre el tema, ampliando los tipos de modalidad tratados para incluir la lógica deóntica y la lógica epistémica. El trabajo seminal de Arthur Prior aplicó el mismo lenguaje formal para tratar la lógica temporal y preparó el camino para la unión de los dos temas. Saul Kripke descubrió (contemporáneamente con Prior) su teoría de la semántica de Kripke, que revolucionó la tecnología formal disponible para los lógicos modales y dio una nueva teoría de grafos forma de ver la modalidad que ha impulsado muchas aplicaciones en lingüística computacional y informática, como la lógica dinámica.
Lógica de predicados[editar]

La lógica de predicados es el término genérico para los sistemas formales simbólicos como la lógica de primer orden, la lógica de segundo orden, la lógica de muchos órdenes y la lógica infinitaria. Proporciona una cuenta de cuantificadores lo suficientemente general para expresar un amplio conjunto de argumentos que ocurren en el lenguaje natural. Por ejemplo, la famosa paradoja del barbero de Bertrand Russell, "hay un hombre que afeita a todos y sólo a los hombres que no se afeitan a sí mismos", puede formalizarse mediante la sentencia , utilizando el predicado no lógico para indicar que x es un hombre, y la relación no lógica para indicar que x afeita a y; todos los demás símbolos de las fórmulas son lógicos, y expresan el cuantificadores universal y existencial, la conjunción, el implicación, la negación y el bicondicional.
Mientras que la lógica silogística aristotélica especifica un pequeño número de formas que puede adoptar la parte relevante de los juicios implicados, la lógica de predicados permite analizar las oraciones en sujeto y argumento de varias formas adicionales, permitiendo a la lógica de predicados resolver el problema de la generalidad múltiple que había dejado perplejos a los lógicos medievales.
El desarrollo de la lógica de predicados suele atribuirse a Gottlob Frege, a quien también se le atribuye el mérito de ser uno de los fundadores de la filosofía analítica, pero la formulación de la lógica de predicados más utilizada hoy en día es la lógica de primer orden presentada en Principios de lógica matemática por David Hilbert y Wilhelm Ackermann en 1928. La generalidad analítica de la lógica de predicados permitió la formalización de las matemáticas, impulsó la investigación de la teoría de conjuntos y permitió el desarrollo del enfoque de Alfred Tarski sobre la teoría de modelos. Proporciona la base de la lógica matemática moderna.
El sistema original de lógica de predicados de Frege era de segundo orden, en lugar de primer orden. La Lógica de segundo orden es defendida de manera más prominente (contra las críticas de Willard Van Orman Quine y otros) por George Boolos y Stewart Shapiro.
Lógica no clásica[editar]
Las lógicas discutidas anteriormente son todas "bivalentes" o "de dos valores"; es decir, se entienden de forma más natural como la división de las proposiciones en verdaderas y falsas. Los sistemas de lógica no clásica son aquellos que rechazan varias reglas de la lógica clásica.
Hegel desarrolló su propia lógica dialéctica que amplió la lógica trascendental de Kant pero también la devolvió a la tierra asegurando que ni en el cielo ni en la tierra, ni en el mundo de la mente ni en el de la naturaleza, existe en ninguna parte un "o" abstracto como el que sostiene el entendimiento. Todo lo que existe es concreto, con diferencia y oposición en sí mismo.[42]
En 1910, Nicolai A. Vasiliev amplió la ley del medio excluido y la ley de la contradicción y propuso la ley del cuarto excluido y la lógica tolerante a la contradicción.[43] A principios del siglo XX, Jan Łukasiewicz investigó la ampliación de los valores tradicionales de verdadero/falso para incluir un tercer valor, "posible" (o indeterminado, una hipótesis) inventando así la lógica ternaria, la primera lógica plurivalente de la tradición occidental.[44] Una modificación menor de la lógica ternaria fue introducida posteriormente en un modelo de lógica ternaria de hermanos propuesto por Stephen Cole Kleene. El sistema de Kleene difiere de la lógica de Łukasiewicz con respecto a un resultado de la implicación. El primero supone que el operador de implicación entre dos hipótesis produce una hipótesis.
Desde entonces se han ideado lógicas como la lógica difusa con un número infinito de "grados de verdad", representados por un número real entre 0 y 1.[45]
La Lógica intuicionista fue propuesta por L.E.J. Brouwer como la lógica correcta para razonar sobre las matemáticas, basándose en su rechazo del principio del tercero excluido como parte de su intuicionismo. Brouwer rechazó la formalización en matemáticas, pero su alumno Arend Heyting estudió la lógica intuicionista formalmente, al igual que Gerhard Gentzen. La lógica intuicionista es de gran interés para los informáticos, ya que es una lógica intuicionista y ve muchas aplicaciones, como la extracción de programas verificados a partir de pruebas y la influencia en el diseño de lenguajes de programación a través de la correspondencia fórmula-como-tipos.
La lógica modal no es condicional de verdad, por lo que a menudo se ha propuesto como una lógica no clásica. Sin embargo, la lógica modal se formaliza normalmente con el principio del medio excluido, y su semántica relacional es bivalente, por lo que esta inclusión es discutible.
Historia[editar]
La historia de la lógica documenta el desarrollo de la lógica en varias culturas y tradiciones a lo largo de la historia. Aunque muchas culturas han empleado intrincados sistemas de razonamiento, e, incluso, el pensamiento lógico estaba ya implícito en Babilonia en algún sentido, la lógica como análisis explícito de los métodos de razonamiento ha recibido un tratamiento sustancial solo originalmente en tres tradiciones: la Antigua China, la Antigua India y la Antigua Grecia.
Aunque las dataciones exactas son inciertas, particularmente en el caso de la India, es probable que la lógica emergiese en las tres sociedades hacia el siglo IV a. C. El tratamiento formalmente sofisticado de la lógica proviene de la tradición griega, especialmente del Organon aristotélico, cuyos logros serían desarrollados por los lógicos islámicos y, luego, por los lógicos de la Edad Media europea. El descubrimiento de la lógica india entre los especialistas británicos en el siglo XVIII influyó también en la lógica moderna.
La historia de la lógica es producto de la confluencia de cuatro líneas de pensamiento, que aparecen en momentos históricos diferentes:[46] La lógica aristotélica, seguida de los aportes de los megáricos y los estoicos. Siglos después, Ramon Llull y Leibniz estudiaron la posibilidad de un lenguaje único, completo y exacto para razonar. Al comienzo del siglo XIX las investigaciones en los fundamentos del álgebra y la geometría, seguidos por el desarrollo del primer cálculo completo por Frege. Ya en el siglo XX, Bertrand Russell y Whitehead culminaron el proceso de creación de la lógica matemática. A partir de este momento no cesarán de producirse nuevos desarrollos y de nacer escuelas y tendencias. Otra perspectiva interesante sobre cómo abordar el estudio de la historia lógica la ofrece Alberto Moretti[47] y que es sintetizada por Diego Letzen.[48]Controversias[editar]
¿Es empírica la lógica?[editar]
¿Cuál es el estatus epistemológico de la leyes de la lógica? ¿Qué tipo de argumento es apropiado para criticar los supuestos principios de la lógica? En un influyente artículo titulado "¿Es empírica la lógica?"[49] Hilary Putnam, basándose en una sugerencia de W. V. Quine, argumentó que en general los hechos de la lógica proposicional tienen un estatus epistemológico similar al de los hechos sobre el universo físico, por ejemplo como las leyes de la mecánica o de la relatividad general, y en particular que lo que los físicos han aprendido sobre la mecánica cuántica proporciona un caso convincente para abandonar ciertos principios familiares de la lógica clásica: si queremos ser realistas sobre los fenómenos físicos descritos por la teoría cuántica, entonces debemos abandonar el principio de distributividad, sustituyendo la lógica clásica por la lógica cuántica propuesta por Garrett Birkhoff y John von Neumann.[50]
Otro trabajo del mismo nombre de Michael Dummett sostiene que el deseo de realismo de Putnam exige la ley de la distributividad.[51] La distributividad de la lógica es esencial para que el realista entienda cómo las proposiciones son verdaderas del mundo de la misma manera que ha argumentado que lo es el principio de bivalencia. De este modo, la pregunta "¿Es la lógica empírica?" puede verse como una respuesta natural a la controversia fundamental en metafísica sobre realismo versus antirrealismo.
Implicación: estricta o material[editar]
La noción de implicación formalizada en la lógica clásica no se traduce cómodamente al lenguaje natural por medio de "si ... entonces ...", debido a una serie de problemas denominados paradojas de la implicación material.
La primera clase de paradojas involucra contrafactuales, tales como Si la luna está hecha de queso verde, entonces 2+2=5, que son desconcertantes porque el lenguaje natural no soporta el principio de explosión. La eliminación de esta clase de paradojas fue la razón de la formulación de C. I. Lewis de la implicación estricta, que finalmente condujo a lógicas más radicalmente revisionistas como la lógica relevante.
La segunda clase de paradojas involucra premisas redundantes, sugiriendo falsamente que conocemos el sucesor debido al antecedente: así, "si ese hombre es elegido, la abuelita morirá" es materialmente verdadero ya que la abuelita es mortal, independientemente de las perspectivas de elección del hombre. Tales oraciones violan la máxima griceana de relevancia, y pueden ser modeladas por lógicas que rechazan el principio de Monotonicidad de la implicación, como la lógica de la relevancia.
Tolerar lo imposible[editar]
Georg Wilhelm Friedrich Hegel fue profundamente crítico con cualquier noción simplificada del Principio de no contradicción. Se basó en la idea de Gottfried Wilhelm Leibniz de que esta ley de la lógica requiere también un fundamento suficiente para especificar desde qué punto de vista (o tiempo) se dice que algo no puede contradecirse. Un edificio, por ejemplo, se mueve y no se mueve; el terreno para lo primero es nuestro sistema solar y para lo segundo la tierra. En la dialéctica hegeliana, la ley de la no-contradicción, de la identidad, se apoya ella misma en la diferencia y, por tanto, no es afirmable de forma independiente.
En estrecha relación con las cuestiones que surgen de las paradojas de la implicación está la sugerencia de que la lógica debe tolerar la inconsistencia. La Lógica relevante y la Lógica paraconsistente son los enfoques más importantes aquí, aunque las preocupaciones son diferentes: una consecuencia clave de la Lógica clásica y de algunos de sus rivales, como la Lógica intuicionista, es que respetan el principio de explosión, lo que significa que la lógica colapsa si es capaz de derivar una contradicción. Graham Priest, el principal defensor del dialeteismo, ha argumentado a favor de la paraconsistencia sobre la base de que existen, de hecho, contradicciones verdaderas.[52]
Rechazo de la verdad lógica[editar]
La vena filosófica de varios tipos de escepticismo contiene muchos tipos de duda y rechazo de las diversas bases sobre las que descansa la lógica, como la idea de forma lógica, la inferencia correcta o el significado, lo que a veces lleva a la conclusión de que no hay verdades lógicas. Esto contrasta con los puntos de vista más habituales en el escepticismo filosófico, donde la lógica dirige la indagación escéptica para dudar de los saberes recibidos, como en la obra de Sexto Empírico.
Friedrich Nietzsche proporciona un fuerte ejemplo del rechazo de la base habitual de la lógica: su rechazo radical de la idealización le llevó a rechazar la verdad como un "... ejército móvil de metáforas, metonimias y antropomorfismos-en resumen ... metáforas que están desgastadas y sin poder sensual; monedas que han perdido sus imágenes y ahora importan sólo como metal, ya no como monedas".[53] Su rechazo de la verdad no le llevó a rechazar por completo la idea de la inferencia o la lógica, sino que sugirió que "la lógica [llegó] a existir en la cabeza del hombre [a partir] de la ilógica, cuyo reino originalmente debe haber sido inmenso [ver voluntarismo]. Innumerables seres que hicieron inferencias de una manera diferente a la nuestra perecieron".[54] Así, existe la idea de que la inferencia lógica tiene una utilidad como herramienta para la supervivencia humana, pero que su existencia no respalda la existencia de la verdad, ni tiene una realidad más allá de lo instrumental: "También la lógica se apoya en supuestos que no se corresponden con nada del mundo real".[55]
Esta posición sostenida por Nietzsche, sin embargo, ha sido sometida a un escrutinio extremo por varias razones. Algunos filósofos, como Jürgen Habermas, afirman que su posición es autorrefutante y acusan a Nietzsche de no tener siquiera una perspectiva coherente, y mucho menos una teoría del conocimiento [ver perspectivismo].[56] Georg Lukács, en su libro La destrucción de la razón, afirma que, "Si estudiáramos las afirmaciones de Nietzsche en este ámbito desde un ángulo lógico-filosófico, nos encontraríamos con un caos vertiginoso de las afirmaciones más escabrosas, arbitrarias y violentamente incompatibles. "[57] Bertrand Russell describió las afirmaciones irracionales de Nietzsche con "Es aficionado a expresarse de forma paradójica y con vistas a escandalizar a los lectores convencionales" en su libro A History of Western Philosophy.[58]
Este rechazo nietzscheano de la base tradicional de la lógica es consistente con el radical rechazo nietzscheano en general del antropomorfismo filosófico, procedente de tradiciones filosóficas tales como el platonismo, el cristianismo y, por extensión de estos, todas las formas del realismo científico, que tradicionalmente han considerado que el hombre tiene algún tipo de facultad(es), casi mágicas, que lo hacen capaz de discernir lo que se ha llamado "la verdad" (o el mundo verdadero) de la ilusión o falsedad (o el mundo aparente) (en la tradición judeocristiana, la concepción del ser humano como hecho "a imagen y semejanza" de Dios). De ahí que, así como Nietzsche llamaba platonismo para el pueblo al cristianismo, llamara también cristianismo sin Dios a la Ilustración y sus ídolos (la ciencia, el realismo científico, la democracia, la idea de progreso, etc.).
Véase también[editar]
- Falacia lógica
- Cálculo lógico
- Lógica de primer orden
- Lógica de segundo orden
- Lógica proposicional
- Lógica matemática
- Lógica computacional
- Lógica modal
- Lógica booleana
- Lógica filosófica
- Lógica clásica
- Lógica no clásica
- Lógica informal
- Lógica dialéctica
- Lógica doxástica
- Lógica deóntica
- Lógica temporal
- Lógica trivalente
- Lógica epistémica
- Lógica difusa
- Lógica plurivalente
- Metodología
- Método científico
- MC-14
- Argumento
- Razón
- Silogismo
- Verdad
- Aporía
- Dialelo
- Paradoja
- Dicotomía
- Nyāya
- Filosofía de la lógica
- Anexo:Símbolos lógicos
- Principio de no contradicción
- Principio de identidad
- Principio del tercero excluido
- Tertium comparationis
- Logos
- Filosofía
Referencias[editar]
- ↑ «Lógica (evolución histórica) - Filosofía.org».
- ↑ Hofweber, Thomas (2023). Zalta, Edward N., ed. Logic and Ontology (Summer 2023 edición). Metaphysics Research Lab, Stanford University. Consultado el 12 de marzo de 2024.
- ↑ Shapiro, Stewart; Kouri Kissel, Teresa (2024). Zalta, Edward N., ed. Classical Logic (Spring 2024 edición). Metaphysics Research Lab, Stanford University. Consultado el 12 de marzo de 2024.
- ↑ Gerogiorgakis, Stamatios (1 de enero de 2013). Jon Williamson & Federica Russo: Key Terms in Logic. Brill | mentis. pp. 384-386. ISBN 978-3-89785-859-6. Consultado el 12 de marzo de 2024.
- ↑ «Logic | Internet Encyclopedia of Philosophy» (en inglés estadounidense). Consultado el 12 de marzo de 2024.
- ↑ Simon Blackburn (ed.). «logic». The Oxford Dictionary of Philosophy (en inglés) (2008 Edition). Oxford University Press. «lógica: La ciencia general de la inferencia.»
- ↑ Corazón González, Rafael. Saber, entender... vivir: una aproximación a la filosofía. pp. 74-77.
- ↑ Quine, Willard Van Orman (1986). Philosophy of Logic (2nd edición). Cambridge, MA.: Harvard University Press. pp. 1–14, 61–75. ISBN 0674665635. JSTOR j.ctvk12scx. OCLC 12664089.
- ↑ McGinn, Colin (2000). Logical Properties: Identity, Existence, Predication, Necessity, Truth. Oxford: Clarendon Press. ISBN 9780199241811. OCLC 44502365. doi:10.1093/0199241813.001.0001.[página requerida]
- ↑ McKeon, Matthew (2003). «Colin McGinn. Logical properties: identity, existence, predication, necessity, truth. Clarendon Press, Oxford 2000, vi + 114 pp.». Bulletin of Symbolic Logic (en inglés) 9 (1): 39-42. ISSN 1079-8986. doi:10.1017/S107989860000473X.
- ↑ Liddell, Henry George, and Robert Scott. 1940. "Logikos." A Greek–English Lexicon, edited by H. S. Jones with R. McKenzie. Oxford: Clarendon Press. – via Perseus Project. Retrieved 9 May 2020.
- ↑ Harper, Douglas. 2020 [2001]. "logic (n.)." Online Etymology Dictionary. Retrieved 9 May 2020.
- ↑ Robert Audi (ed.). «Inference». The Cambridge Dictionary of Philosophy (en inglés) (2nd Edition). Cambridge University Press.
- ↑ «formal system». Encyclopedia Britannica (en inglés). Consultado el 3 de agosto de 2009.
- ↑ «inference». The Oxford Companion to Philosophy (en inglés). Oxford University Press. 2005. Consultado el 1º de agosto de 2009.
- ↑ Error en la cita: Etiqueta
<ref>no válida; no se ha definido el contenido de las referencias llamadasInferencia Consequence - ↑ Beall, J. C.; Restall, Greg. «Logical Consequence». En Edward N. Zalta, ed. Stanford Encyclopedia of Philosophy (en inglés) (Summer 2009 Edition).
- ↑ Otero, Carlos Peregrín (1989). Introducción a la lingüística transformacional. Siglo XXI. p. 213. ISBN 978-968-23-1541-1.
- ↑ a b Hamblin, Charles Leonard (1970). Fallacies. Methuen.
- ↑ Groarke, Leo. «Informal Logic». En Edward N. Zalta, ed. Stanford Encyclopedia of Philosophy (en inglés) (Spring 2013 Edition).
- ↑ Hansen, Hans Vilhelm (2002). «The Straw Thing of Fallacy Theory: The Standard Definition of 'Fallacy'». Argumentation 16 (2): 133-155.
- ↑ Kenneth, S. Pope (2003). «Logical Fallacies in Psychology: 22 Types» (en inglés). Consultado el 14 de junio de 2013.
- ↑ ARP. Sociedad para el Avance del Pensamiento Crítico. Falacias lógicas
- ↑ Real Academia Española. «paradoja». Diccionario de la lengua española (23.ª edición).
- ↑ "Paradojas Y Sofismas Físicos" V. Langue, Ed. Mir, Moscú 1984: 11.
- ↑ Robert Audi (ed.). «paradox». The Cambridge Dictionary of Philosophy (en inglés) (2nd Edition). Cambridge University Press. «A seemingly sound piece of reasoning based on seemingly true assuptions that leads to a contradiction (or other obviously false conclusión).»
- ↑ Padilla Gálvez, Jesús (2017). «Capítulo III. La paradoja del mentiroso». Verdad. Controversias abiertas. Valencia: Tirant Humanidades. pp. 195 y ss.
- ↑ Merriam-Webster's Online Dictionary, truth, 2005.
- ↑ Real Academia Española. «Verdad». Diccionario de la lengua española (23.ª edición).
- ↑ Cfr. Parménides, Platón, Hegel y, en general, los idealismos
- ↑ Ferrater Mora. op. cit. p. 3397 y ss.
- ↑ Etimologías e interpretaciones de sentido de verdad en hebreo, griego, latín, germánico, e indioiraní, véase: Zubiri, X. Naturaleza, Historia, Dios. Nuestra situación intelectual. La verdad y la ciencia. op. cit. p.14
- ↑ Tema de investigación transversal
- ↑ Arrancando desde la física hasta la neurología, pasando por el evolucionismo y la genética y la biología y la etología, psicología etc.
- ↑ Tal como ya definió Platón el conocimiento como ciencia: creencias u opiniones verdaderas y justificables con la razón. Teeteto, 201c-210b
- ↑ epistemología y metodología e investigación
- ↑ Evandro Agazzi, 1986.
- ↑ Łukasiewicz, Jan (1957). Aristotle's syllogistic from the standpoint of modern formal logic (2nd ed.). Oxford University Press. p. 7. ISBN 978-0-19-824144-7
- ↑ a b c Brody, Boruch A. (2006). org/oclc/61151356 Enciclopedia de filosofía 5. Donald M. Borchert (2ª edición). Detroit: Thomson Gale/Macmillan Reference USA. pp. 535-536. ISBN 0-02-865780-2. OCLC 61151356. «Los dos tipos más importantes de cálculos lógicos son los cálculos proposicionales (o sentenciales) y los cálculos funcionales (o de predicados). Un cálculo proposicional es un sistema que contiene variables y conectivas proposicionales (algunos también contienen constantes proposicionales) pero no variables o constantes individuales o funcionales. En el cálculo proposicional extendido se añaden cuantificadores cuyas variables operativas son variables proposicionales.»
- ↑ Brody, Boruch A. (2006). Enciclopedia de filosofía 5. Donald M. Borchert (2nd edición). Detroit: Thomson Gale/Macmillan Reference USA. pp. 535-558. ISBN 0-02-865780-2. OCLC 61151356. «Axioma. Proposición básica en un sistema formal que se afirma sin prueba y de la que, junto con las demás proposiciones de este tipo, se derivan todos los demás teoremas según las reglas de inferencia del sistema...Prueba. Para una fórmula bien formada A en un sistema logístico dado, una prueba de A es una secuencia finita de fórmulas bien formadas la última de las cuales es A y cada una de las cuales es un axioma del sistema o puede deducirse de los miembros anteriores de la secuencia según las reglas de inferencia del sistema...Teorema. Cualquier fórmula bien formada de un sistema logístico dado para el que existe una prueba en el sistema.»
- ↑ «Historia de la lógica: Lógica árabe». Encyclopædia Britannica. Archivado desde el original el 12 de octubre de 2007.
- ↑ Hegel, G.W.F (1971) [1817]. Philosophy of Mind. Encyclopedia of the Philosophical Sciences. trans. William Wallace. Oxford: Clarendon Press. p. 174. ISBN 978-0-19-875014-7.
- ↑ Joseph E. Brenner (3 August 2008). Logic in Reality. Springer. pp. 28–30. ISBN 978-1-4020-8374-7. Retrieved 9 April 2012.
- ↑ Zegarelli, Mark (2010). Lógica para Dummies. John Wiley & Sons. p. 30. ISBN 978-1-118-05307-2.
- ↑ Hájek, Petr (2006). "Fuzzy Logic". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
- ↑ Izuzquiza Otero, Ignacio; Corellano Aznar, Luis; Frechilla García, Ana Rosa; Peña Calvo, José Vicente; Villamayor Lloro, Santiago (2008). «El Universo de la lógica». En Achón, Elena; Álvarez, Gema, eds. Filosofía y ciudadanía (Manuel Andaluz edición). Madrid: Grupo Anaya Sociedad Anónima. p. 310. ISBN 9788466773195.
- ↑ Lozano, Gabriel Vargas (29 de diciembre de 2018). «LA FILOSOFÍA DE LA PRAXIS. DOS CONCEPCIONES: ANTONIO GRAMSCI Y ADOLFO SÁNCHEZ VÁZQUEZ». Revista Dialectus - Revista de Filosofia (13). ISSN 2317-2010. doi:10.30611/2018n13id40082. Consultado el 21 de junio de 2021.
- ↑ Letzen, Diego (15 de diciembre de 2020). «Las lógicas y los lógicos». Análisis Filosófico 40 (Especial): 133-157. ISSN 1851-9636. doi:10.36446/af.2020.430. Consultado el 21 de junio de 2021.
- ↑ Error en la cita: Etiqueta
<ref>no válida; no se ha definido el contenido de las referencias llamadas¿Es la lógica empírica? - ↑ Error en la cita: Etiqueta
<ref>no válida; no se ha definido el contenido de las referencias llamadasLa lógica de la mecánica cuántica - ↑ Error en la cita: Etiqueta
<ref>no válida; no se ha definido el contenido de las referencias llamadasLa verdad y otros enigmas - ↑ Error en la cita: Etiqueta
<ref>no válida; no se ha definido el contenido de las referencias llamadasstanford7 - ↑ Error en la cita: Etiqueta
<ref>no válida; no se ha definido el contenido de las referencias llamadasnietzsche - ↑ Error en la cita: Etiqueta
<ref>no válida; no se ha definido el contenido de las referencias llamadasnietzsche8 - ↑ Error en la cita: Etiqueta
<ref>no válida; no se ha definido el contenido de las referencias llamadasnietzsche9 - ↑ Error en la cita: Etiqueta
<ref>no válida; no se ha definido el contenido de las referencias llamadasnietzsche10 - ↑ Error en la cita: Etiqueta
<ref>no válida; no se ha definido el contenido de las referencias llamadasmarxists - ↑ Russell, Bertrand (1945), A History of Western Philosophy And Its Connection with Political and Social Circumstances from the Earliest Times to the Present Day, Simon and Schuster, p. 762, archivado desde el original el 28 de mayo de 2014.
Bibliografía adicional[editar]
- Deaño, Alfredo (1974). Introducción a la lógica formal 1. La lógica de enunciados. Madrid: Alianza Editorial.
- Deaño, Alfredo (1974). Introducción a la lógica formal 2. La lógica de predicados. Madrid: Alianza Editorial.
- Deaño, Alfredo (1980). Las concepciones de la lógica. Madrid: Taurusl.
- Ferrater Mora, J. (1984). Diccionario de Filosofía (4 tomos). Barcelona. Alianza Diccionarios. ISBN 84-206-5299-7.
- Honderich, T.(Editor) (2001). Enciclopedia Oxford de Filosofía. Trd. Carmen García Trevijano. Madrid. Editorial Tecnos. ISBN 84-309-3699-8.
- Mosterín, Jesús (1970 y 1976). Lógica de primer orden. Barcelona. Ariel. ISBN 84-344-3939-5.
- Padilla Gálvez, J. (2017). Verdad. Controversias Abiertas. Valencia: Tirant Lo Blanch. ISBN 978-84-17069-58-2.
- Priest, Graham (2008). An introduction to non-classical logic: From if to is (2ª edición). Nueva York: Cambridge University Press. ISBN 978-0521854337. Archivado desde el original el 23 de agosto de 2017. Consultado el 22 de agosto de 2017.
- Sacristán, Manuel (1976). Introducción a la lógica y al análisis formal. Barcelona: Ariel. ISBN 84-344-3901-8.
- Barwise, J. (1982). Handbook of Mathematical Logic. Elsevier. isbn: 978-0-08-093364-1.
- Belnap, N. (1977). "A useful four-valued logic". In Dunn & Eppstein, Modern uses of multiple-valued logic. Reidel: Boston.
- Bocheński, J.M. (1959). A précis of mathematical logic. Translated from the French and German editions by Otto Bird. D. Reidel, Dordrecht, South Holland.
- Bocheński, J.M. (1970). A history of formal logic. 2nd Edition. Translated and edited from the German edition by Ivo Thomas. Chelsea Publishing, New York.
- Brookshear, J. Glenn (1989). Theory of computation: formal languages, automata, and complexity. Redwood City, Calif.: Benjamin/Cummings Pub. Co. ISBN 978-0-8053-0143-4.
- Cohen, R.S, and Wartofsky, M.W. (1974). Logical and Epistemological Studies in Contemporary Physics. Boston Studies in the Philosophy of Science. D. Reidel Publishing Company: Dordrecht, Netherlands. isbn:90-277-0377-9.
- Finkelstein, D. (1969). "Matter, Space, and Logic". in R.S. Cohen and M.W. Wartofsky (eds. 1974).
- Gabbay, D.M., and Guenthner, F. (eds., 2001–2005). Handbook of Philosophical Logic. 13 vols., 2nd edition. Kluwer Publishers: Dordrecht.
- Haack, Susan (1996). Deviant Logic, Fuzzy Logic: Beyond the Formalism, University of Chicago Press.
- Harper, Robert (2001). «Logic». Online Etymology Dictionary. Consultado el 8 de mayo de 2009.
- Hilbert, D., and Ackermann, W, (1928). Grundzüge der theoretischen Logik (Principles of Mathematical Logic). Springer-Verlag. OCLC 2085765
- Hodges, W. (2001). Logic. An introduction to Elementary Logic, Penguin Books.
- Hofweber, T. (2004), Logic and Ontology. Stanford Encyclopedia of Philosophy. Edward N. Zalta (ed.).
- Hughes, R.I.G. (1993, ed.). A Philosophical Companion to First-Order Logic. Hackett Publishing.
- Kline, Morris (1972). Mathematical Thought From Ancient to Modern Times. Oxford University Press. ISBN 978-0-19-506135-2.
- Kneale, William, and Kneale, Martha, (1962). The Development of Logic. Oxford University Press, London, UK.
- Liddell, Henry George; Scott, Robert. «Logikos». A Greek-English Lexicon. Perseus Project. Consultado el 8 de mayo de 2009.
- Mendelson, Elliott, (1964). Introduction to Mathematical Logic. Wadsworth & Brooks/Cole Advanced Books & Software: Monterey, Calif. OCLC 13580200
- Smith, B. (1989). "Logic and the Sachverhalt". The Monist 72(1): 52–69.
- Whitehead, Alfred North and Bertrand Russell (1910). Principia Mathematica. Cambridge University Press: Cambridge, England. OCLC 1041146
Enlaces externos[editar]
 Wikcionario tiene definiciones y otra información sobre lógica.
Wikcionario tiene definiciones y otra información sobre lógica.- Aprende Lógica (Autor: Francisco José Calzado Fernández)
- Breve Historia de la Lógica
- Esta obra contiene una traducción parcial derivada de «Logic» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
- Esta obra contiene una traducción parcial derivada de «Logic» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
Error en la cita: Existen etiquetas <ref> para un grupo llamado «lower-roman», pero no se encontró la etiqueta <references group="lower-roman"/> correspondiente.







