Lógica computacional
La lógica computacional es la misma lógica matemática aplicada al contexto de las ciencias de la computación. Su uso es fundamental en varios niveles: en los circuitos computacionales, en la programación lógica y en el análisis y optimización (de recursos temporales y espaciales) de algoritmos.
La lógica se extiende al corazón de la informática a medida que surge como una disciplina: El trabajo de Alan Turing sobre el Entscheidungsproblem seguido del trabajo de Kurt Gödel sobre teoremas incompletos. La noción de la computadora de uso general que surgió de este trabajo fue de gran importancia para los diseñadores de la maquinaria informática en la década de 1940.
En los años 50 y 60, investigaciones predijeron que, cuando el conocimiento humano se pudiera expresar usando la lógica con notaciones matemáticas, sería posible crear una máquina capaz de razonar o una inteligencia artificial. Esto fue más difícil de lo esperado a causa de la complejidad del razonamiento humano. En la lógica de programación, un programa consiste en una colección de axiomas y reglas. Los sistemas de programación lógicos (como Prolog) calculan las consecuencias de los axiomas y las reglas organizadas para responder a una consulta.
Hoy en día, la lógica es extensamente aplicada en los campos de inteligencia artificial y de ciencias de computación, y estos campos proporcionan una rica fuente de problemas en la lógica formal e informal. La teoría de la argumentación es un buen ejemplo de cómo la lógica está siendo aplicada a la inteligencia artificial. El sistema de clasificación computacional ACM, en particular, considera:
- Sección F.3 en Lógicas y significados de programas y F.4 en Lógica matemática y lenguajes formales como parte de la teoría de la ciencia de computación: este trabajo cubre la semántica formal de los lenguajes de programación tan bien como el trabajo de métodos formales como la lógica de Hoare.
- Lógica booleana como fundamento en el hardware de la computadora, particularmente la sección del sistema B.2 en la estructura aritmética y lógica, relacionado con operadores AND, NOT y OR.
- Muchos formalismos lógicos fundamentales son esenciales para la sección I.2 sobre inteligencia artificial, por ejemplo la lógica modal y la lógica por defecto en los formalismos y métodos de representación del conocimiento, las cláusulas de Horn en la programación lógica y la lógica de descripción.
Además, las computadoras se pueden usar como herramientas para los lógicos. Por ejemplo, en lógica simbólica y lógica matemática, las pruebas de los seres humanos pueden ser asistidas por computadoras. Usando la prueba automatizada del teorema, las máquinas pueden encontrar y comprobar pruebas, así como trabajar con las pruebas demasiadas largas como para escribir a mano.
Circuitos computacionales[editar]
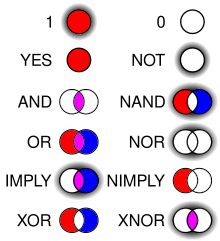
El nivel menos abstracto dentro de una computadora está constituido por circuitos electrónicos que responden a diferentes señales eléctricas, siguiendo los patrones de la lógica booleana; esto es, compuertas lógicas que devuelven un valor dependiendo de las entradas que se le dan al sistema. Existen ocho compuertas lógicas básicas con las cuales se pueden formar sistemas muy complejos: AND, OR, Inverter, Buffer, NAND, NOR, XOR y XNOR. Todas ellas son representadas mediante un símbolo y una tabla de valores de verdad, que es simplemente un cuadro donde se ubican todas las posibles entradas y los valores que devolvería la compuerta dados dichos valores.
Todo sistema computacional, por muy complejo que sea, no está compuesto por más que circuitos electrónicos que únicamente entienden un lenguaje binario. La lógica computacional se encarga de modelar y optimizar tales sistemas a este nivel.
Referencias[editar]
Enlaces externos[editar]
- Esta obra contiene una traducción parcial derivada de «Logic» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
