Número
Un número es un concepto abstracto que se emplea para contar (cantidades), medir (magnitudes) y etiquetar. Los números más sencillos, que utilizamos todos en la vida cotidiana, son los números naturales: 1, 2, 3, etc. Se denotan mediante y sirven también como ordinales, para establecer un orden (primero, segundo,...). En ocasiones usamos el término número para hablar de lo que en realidad es un numeral o cifra (por ejemplo, nuestros números arábigos). Desde un punto de vista totalmente general un número es cualquier elemento de una estructura lógico-matemática conocida como sistema numérico.
Los números desempeñan un papel fundamental en las ciencias empíricas; no solo los naturales, sino muchos otros tipos de números que contemplan las matemáticas. El conjunto de números enteros (representados por ) es una ampliación de los naturales, incluyendo los negativos (que utilizamos para representar deudas, y en los termómetros para las temperaturas bajo cero). Si incluimos los números fraccionarios (1/3, 0,75, -3,25, etc.) se obtiene el conjunto de los números racionales, cuyo símbolo es . Ya en la Antigüedad se descubrió que existen números no racionales: la diagonal de un cuadrado de lado 1 mide raíz de 2, un número que no puede representarse como número entero ni como fracción; es irracional. Los racionales junto con los irracionales forman el conjunto de los números reales, (ℝ). Posteriormente, se han ido agregando otros tipos de números: imaginarios, trascendentes, irreales, complejos...
Nótese que la teoría de números es una rama de las matemáticas que se ocupa de los enteros (no de números en general). El origen de los números es que los primeros números que el hombre inventó fueron los números naturales, los cuales se utilizaban y se utilizan para contar elementos de un conjunto finito, ya que se procede a enumerar dichos elementos de una manera ordenada seleccionándolos uno tras otro a la vez que se le atribuye a cada uno un número.
Tipos de números[editar]
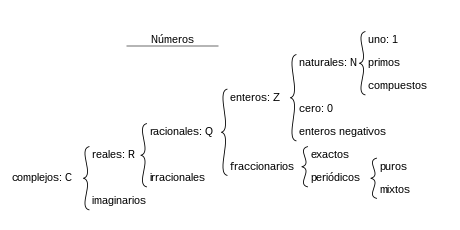
Los números más conocidos son los números naturales. Denotados mediante , son conceptualmente los más simples y los que se usan para contar unidades discretas. Estos, conjuntamente con los números «negativos», conforman el conjunto de los enteros, denotados mediante (del alemán Zahlen, ‘números’). Los números naturales negativos permiten representar formalmente deudas, y generalizar la resta de cualesquiera dos números naturales. Es decir, ya tenemos solución para operaciones como, por ejemplo, 3-2 = 1.
Otro tipo de números ampliamente usados son números fraccionarios, los cuales representan tanto cantidades inferiores a una unidad, como números mixtos (un conjunto de unidades más una parte inferior a la unidad). Los números fraccionarios pueden ser expresados siempre como cocientes de enteros. El conjunto de todos los números fraccionarios es el conjunto de los números racionales (que usualmente se define para que incluya tanto a los racionales positivos, como a los racionales negativos y el cero). Este conjunto de números se designa como . Al igual que con los números enteros se puede calcular el resultado de cualquier resta, con los racionales es posible efectuar divisiones que no tienen resultado entero, como 15/2 = 7,5 o 7½.
Los números racionales permiten resolver gran cantidad de problemas prácticos, pero desde los antiguos griegos se conoce que ciertas relaciones geométricas (la diagonal de un cuadrado de lado unidad) son números no enteros que tampoco son racionales. Igualmente, la solución numérica de una ecuación polinómica cuyos coeficientes son números racionales, usualmente es un número no racional. Puede demostrarse que cualquier número irracional puede representarse como una sucesión de Cauchy de números racionales que se aproximan a un límite numérico. El conjunto de todos los números racionales y los irracionales (obtenidos como límites de sucesiones de Cauchy de números racionales) es el conjunto de los números reales . Durante un tiempo se pensó que toda magnitud física existente podía ser expresada en términos de números reales exclusivamente. Entre los reales, existen números que no son soluciones de una ecuación polinomial o algebraica, y estos reciben el nombre de transcendentales. Los más conocidos de estos números son el número π (Pi) y el número e (este último base de los logaritmos naturales), los cuales están relacionados entre sí por la identidad de Euler.
Uno de los problemas de los números reales es que no forman un cuerpo algebraicamente cerrado, por lo que ciertos problemas no tienen solución planteados en términos de números reales. Esa es una de las razones por las cuales se introdujeron los números complejos , que son el mínimo cuerpo algebraicamente cerrado que contiene a los números reales. Además, en algunas aplicaciones prácticas, así como en las formulaciones estándar de la mecánica cuántica se considera útil introducir los números complejos. Al parecer, la estructura matemática de los números complejos refleja estructuras existentes en problemas físicos, por lo que en física teórica y en diversas aplicaciones los números complejos se usan en pie de igualdad con los números reales, a pesar de que inicialmente fueron considerados únicamente como un artificio matemático sin relación con la realidad física. Todos los conjuntos de números fueron de alguna manera «descubiertos» o sugeridos en conexión con problemas planteados en problemas físicos o en el seno de la matemática elemental y todos ellos parecen tener importantes conexiones con la realidad física.
Al margen de los números reales y complejos, claramente conectados con problemas de las ciencias naturales, existen otros tipos de números que generalizan aún más y extienden el concepto de número de una manera más abstracta y responden más a creaciones deliberadas de matemáticos. La mayoría de estas generalizaciones del concepto de número se usan solo en matemáticas, aunque algunos de ellos han encontrado aplicaciones para resolver ciertos problemas físicos. Entre ellos están los números hipercomplejos, que incluyen a los cuaterniones, útiles para representar rotaciones en un espacio de tres dimensiones, y generalizaciones de estos, como octoniones y los sedeniones.
A un nivel un poco más abstracto también se han ideado conjuntos de números capaces de tratar con cantidades infinitas e infinitesimales, como los hiperreales y los transfinitos. E igualmente los números racionales pueden extenderse de otras maneras, como por ejempo para formar los números p-ádicos, entre los cuales se encuentran los enteros p-ádicos , los racionales p-ádicos o los complejos p-ádicos , que satisfacen .
Lista de los tipos de números existentes[editar]
La teoría de los números trata básicamente de las propiedades de los números naturales y los enteros, mientras que las operaciones del álgebra y el cálculo permiten definir la mayor parte de los sistemas numéricos, entre los cuales están:
- Números naturales
- Números enteros
- Números racionales
- Números reales
- Extensiones de los números reales
- Números usados en teoría de conjuntos
- Números ordinales
- Números cardinales
- Números transfinitos
Estructura de los sistemas numéricos[editar]
En álgebra abstracta y análisis matemático un sistema numérico se caracteriza por una:
- Estructura algebraica, usualmente un anillo conmutativo o cuerpo matemático (en el caso no conmutativo son un álgebra sobre un cuerpo y en el caso de los números naturales solo un monoide conmutativo).
- Estructura de orden, usualmente un conjunto ordenado, en el caso de los números naturales, enteros, racionales y reales se trata de conjuntos totalmente ordenados, aunque los números complejos e hipercomplejos solo son conjuntos parcialmente ordenados. Los reales además son un conjunto bien ordenado y con un orden denso.[1]
- Estructura topológica, los conjuntos numéricos numerables usualmente son conjuntos disconexos, sobre los que se considera la topología discreta, mientras que sobre los conjuntos no numerables se considera una topología que los hace adecuados para el análisis matemático.
Otra propiedad interesante de muchos conjuntos numéricos es que son representables mediante diagramas de Hasse, diagramas de Euler y diagramas de Venn, pudiéndose tomar una combinación de ambos en un diagrama de Euler-Venn con la forma característica de cuadrilátero y además pudiéndose representar internamente un diagrama de Hasse (es una recta). Tanto históricamente como conceptualmente, los diversos conjuntos numéricos, desde el más simple de los números naturales, hasta extensiones transcendentes de los números reales y complejos, elaboradas mediante la teoría de modelos durante el siglo XX, se construyen desde una estructura más simple hasta otra más compleja.[2]
Números naturales especiales[editar]
El estudio de ciertas propiedades que cumplen los números ha producido una enorme cantidad de tipos de números, la mayoría sin un interés matemático específico. Se pueden encuadrar dentro de la matemática recreativa. A continuación se indican algunos:
- Perfecto: número igual a la suma de sus divisores (incluyendo el 1). Ejemplo: 6 = 1 + 2 + 3.
- Sheldon: el número 73, es el 21° número primo, que al multiplicar 7 × 3 = 21; Y al dar la vuelta a sus dígitos da 37 que es el 12° número primo.
- Narcisista: número de n dígitos que resulta ser igual a la suma de las potencias de orden n de sus dígitos. Ejemplo: 153 = 1³ + 5³ + 3³.
- Omirp: número primo que al invertir sus dígitos da otro número primo. Ejemplo: 1597 y 7951 son primos.
- Vampiro: número que es el producto de dos números obtenidos a partir de sus dígitos. Ejemplo: 2187 = 27 × 81.
- Hamsteriano: Su estructura aritmética N= (a×b)2-1, donde a y b son primos los dos, la suma de sus divisores sobrepasa N, y la cantidad de sus divisores es > a×b/2; va como ejemplo: 1224 = (5×7)2-1
- Pitagórico: una terna pitagórica son tres números que cumplen las siguientes condiciones: el cuadrado de uno de ellos, más el cuadrado de otro, es igual al cuadrado del tercero, por ejemplo: (3, 4, 5) ya que 32 + 42 = 9 + 16 = 25 = 52
Una vez entendido el problema de la naturaleza y la clasificación de los números, surge otro, más práctico, pero que condiciona todo lo que se va a hacer con ellos: la manera de escribirlos. El sistema que se ha impuesto universalmente es la numeración posicional, gracias al invento del cero, con una base constante.
Más formalmente, en Los fundamentos de la aritmética, Gottlob Frege (1848-1925) realiza una definición de «número», la cual fue tomada como referencia por muchos matemáticos (entre ellos Bertrand Russell [1872-1870], cocreador de Principia mathematica):
«n» es un número, es entonces la definición de «que existe un concepto “F” para el cual “n” aplica», que a su vez se ve explicado como que «n» es la extensión del concepto «equinumerable con» para «F», y dos conceptos son equinumerables si existe una relación «uno a uno» (véase que no se utiliza el símbolo «1» porque no está definido aún) entre los elementos que lo componen (es decir, una biyección en otros términos).
Véase también que Frege, tanto como cualquier otro matemático, se ve inhabilitado para definir al número como la expresión de una cantidad, porque la simbología matemática no hace referencia necesaria a la numerabilidad, y el hecho de «cantidad» referiría a algo numerable, mientras que números se adoptan para definir la cardinalidad de, por ejemplo, los elementos que se encuentran en el intervalo abierto (0, 1), que contiene innumerables elementos (el continuo).
Peano, antes de establecer sus cinco proposiciones sobre los números naturales, explícita que supone sabida una definición (quizás debido a su «obviedad») de las palabras o conceptos cero, sucesor y número. De esta manera postula:
- 0 es un número natural
- el sucesor de todo número es un número
- dos números diferentes no tienen el mismo sucesor
- 0 no es el sucesor de ningún número
- y la propiedad inductiva
Sin embargo, si uno define el concepto cero como el número 100, y el concepto número como los números mayores a 100, entonces las cinco proposiciones mencionadas anteriormente aplican, no a la idea que Peano habría querido comunicar, sino a su formalización.
La definición de número se encuentra por ende no totalmente formalizada, aunque se encuentre un acuerdo mayoritario en adoptar la definición enunciada por Frege.
Historia del concepto de número[editar]

Cognitivamente el concepto de número está asociado a la habilidad de contar y comparar cuál de dos conjuntos de entidades similares tiene mayor cantidad de elementos. Las primeras sociedades humanas se encontraron muy pronto con el problema de determinar cuál de dos conjuntos era «mayor» que otro, o de conocer con precisión cuántos elementos formaban una colección de cosas. Esos problemas podían ser resueltos simplemente contando. La habilidad de contar del ser humano, no es un fenómeno simple, aunque la mayoría de culturas tienen sistemas de cuenta que llegan como mínimo a centenares, algunos pueblos con una cultura material simple, solo disponen de términos para los números 1, 2 y 3 y usualmente usan el término «muchos» para cantidades mayores, aunque cuando es necesario usan recursivamente expresiones traducibles como «3 más 3 y otros 3».
El conteo se debió iniciar mediante el uso de objetos físicos (tales como montones de piedras) y de marcas de cuenta, como las encontradas en huesos tallados: el de Lebombo, con 29 muescas grabadas en un hueso de babuino, tiene unos 37 000 años de antigüedad y otro hueso de lobo encontrado en la antigua Checoslovaquia, con 57 marcas dispuestas en cinco grupos de 11 y dos sueltas, se ha estimado en unos 30 000 años de antigüedad. Ambos casos constituyen una de las más antiguas marcas de cuenta conocidas habiéndose sugerido que pudieran estar relacionadas con registros de fases lunares.[3] En cuanto al origen ordinal algunas teorías lo sitúan en rituales religiosos. Los sistemas numerales de la mayoría de familias lingüísticas reflejan que la operación de contar estuvo asociado al conteo de dedos (razón por la cual los sistemas de base decimal y vigesimal son los más abundantes), aunque está testimoniado el empleo de otras bases numéricas.
El paso hacia los símbolos numerales, al igual que la escritura, se ha asociado a la aparición de sociedades complejas con instituciones centralizadas constituyendo artificios burocráticos de contabilidad en registros impositivos y de propiedades. Su origen estaría en primitivos símbolos con diferentes formas para el recuento de diferentes tipos de bienes como los que se han encontrado en Mesopotamia inscritos en tablillas de arcilla que a su vez habían venido a sustituir progresivamente el conteo de diferentes bienes mediante fichas de arcilla (constatadas al menos desde el 8000 a. C.) Los símbolos numerales más antiguos encontrados se sitúan en las civilizaciones mesopotámicas usándose como sistema de numeración ya no solo para la contabilidad o el comercio sino también para la agrimensura o la astronomía como, por ejemplo, registros de movimientos planetarios.[4]
En conjunto, desde hace 5000 años la mayoría de las civilizaciones han contado como lo hacemos hoy aunque la forma de escribir los números (si bien todos representan con exactitud los naturales) ha sido muy diversa. Básicamente la podemos clasificar en tres categorías:
- Sistemas de notación aditiva. Acumulan los símbolos de todas las unidades, decenas, centenas, …, necesarios hasta completar el número. Aunque los símbolos pueden ir en cualquier orden, adoptaron siempre una determinada posición (de más a menos). De este tipo son los sistemas de numeración: egipcio, hitita, cretense, romano, griego, armenio y judío.
- Sistemas de notación híbrida. Combinan el principio aditivo con el multiplicativo. En los anteriores 500 se representa con 5 símbolos de 100, en estos se utiliza la combinación del 5 y el 100. El orden de las cifras es ahora fundamental (estamos a un paso del sistema posicional). De este tipo son los sistemas de numeración: chino clásico, asirio, armenio, etíope y maya. Este último utilizaba símbolos para el 1, el 5 y el 0. Siendo este el primer uso documentado del cero tal como lo conocemos hoy (año 36 a. C.) ya que el de los babilonios solo se utilizaba entre otros dígitos.
- Sistemas de notación posicional. La posición de las cifras nos indica si son unidades, decenas, centenas, …, o en general la potencia de la base. Solo tres culturas además de la india lograron desarrollar un sistema de este tipo: el sistema chino (300 a. C.) que no disponía de 0, el sistema babilónico (2000 a. C.) con dos símbolos, de base 10 aditivo hasta el 60 y posicional (de base 60) en adelante, sin 0 hasta el 300 a. C.
Las fracciones unitarias egipcias (Papiro de Ahmes/Rhind)[editar]
En este papiro adquirido por Alexander Henry Rhind (1833-1863) en 1858, cuyo contenido data del 2000 al 1800 a. C. además del sistema de numeración antes descrito nos encontramos con su tratamiento de las fracciones. No consideran las fracciones en general, solo las fracciones unitarias (inversas de los naturales 1/20) que se representan con un signo oval encima del número, la fracción 2/3 que se representa con un signo especial y en algunos casos fracciones del tipo . Hay tablas de descomposición de desde n=1 hasta n=101, como por ejemplo o , no sabemos por qué no utilizaban pero parece que trataban de utilizar fracciones unitarias menores que .
Al ser un sistema sumativo la notación es: 1+1/2+1/4. La operación fundamental es la suma y nuestras multiplicaciones y divisiones se hacían por «duplicaciones» y «mediaciones», por ejemplo 69×19=69×(16+2+1), donde 16 representa 4 duplicaciones y 2 una duplicación.
Fracciones sexagesimales babilónicas (documentos cuneiformes)[editar]
En las tablillas cuneiformes de la dinastía Hammurabi (1800-1600 a. C.) aparece el sistema posicional, antes referido, extendido a las fracciones, pero XXX vale para , o con una representación basada en la interpretación del problema.
Para calcular recurrían, como nosotros antes de disponer de máquinas, a las numerosas tablas que disponían: De multiplicar, de inversos, de cuadrados y cubos, de raíces cuadradas y cúbicas, de potencias sucesivas de un número dado no fijo, etc. Por ejemplo, para calcular , tomaban su mejor aproximación entera , y calculaban (una mayor y otra menor) y entonces es mejor aproximación, procediendo igual obtenemos y obteniendo en la tablilla Yale-7289 2=1;24,51,10 (en base decimal 1,414222) como valor de partiendo de (véase algoritmo babilónico).
Realizaban las operaciones de forma parecida a hoy, la división multiplicando por el inverso (para lo que utilizan sus tablas de inversos). En la tabla de inversos faltan los de 7 y 11 que tienen una expresión sexagesimal infinitamente larga. Sí están 1/59=;1,1,1 (nuestro 1/9=0,111…) y 1/61=;0,59,0,59 (nuestro 1/11=0,0909…), pero no se percataron del desarrollo periódico.
Descubrimiento de los inconmensurables[editar]
Las circunstancias y la fecha de este descubrimiento son inciertas, aunque se atribuye a la escuela pitagórica (se utiliza el teorema de Pitágoras). Aristóteles (384-322 a. C.) menciona una demostración de la inconmensurabilidad de la diagonal de un cuadrado con respecto a su lado basada en la distinción entre lo par y lo impar. La reconstrucción que realiza C. Boyer es:
Sean d:diagonal, s:lado y d/s racional, que podremos escribirlo como , con p y q primos entre sí. Por el teorema de Pitágoras tenemos que , , entonces y por tanto debe ser par y también p, y por tanto q impar. Al ser p par tenemos , entonces y , entonces es par y q también, entonces q es par e impar con lo que tenemos una contradicción.
La teoría pitagórica de todo es número quedó seriamente dañada.
El problema lo resolvería Eudoxo de Cnido (408-355 a. C.) tal como nos indica Euclides en el libro V de Los elementos. Para ello estableció el axioma de Arquímedes: «Dos magnitudes tienen una razón si se puede encontrar un múltiplo de una de ellas que supere a la otra» (excluye el 0). Después, en la definición 5, da la famosa formulación de Eudoxo:
«Dos magnitudes están en la misma razón si dados dos números naturales cualesquiera m y n, si entonces (definición que intercambiando el 2º y 3º términos equivale a nuestro procedimiento actual).
En el libro Historia de la matemética (1985), de J. P. Colette, se hace la observación de que esta definición está muy próxima a la de número real que dará Dedekind (1831-1916), divide las fracciones en las tales que y las que no.
Creación del cero[editar]
En cualquier sistema de numeración posicional surge el problema de la falta de unidades de determinado orden. Por ejemplo, en el sistema babilónico el número escrito en base 60 puede ser o . A veces, se utilizaba la posición vacía para evitar este problema 3 _ 2; pero los escribas debían tener mucho cuidado para no equivocarse.
Hacia el siglo III a. C., en Grecia, se comenzó a representar la nada mediante una "o" que significa oudos 'vacío', y que no dio origen al concepto de cero como existe hoy en día. La idea del cero como concepto matemático parece haber surgido en la India antes que en ningún otro lugar. La única notación ordinal del viejo mundo fue la sumeria, donde el cero se representaba por un vacío.
En América, la primera expresión conocida del sistema de numeración vigesimal prehispánico data del siglo III a. C. Se trata de una estela olmeca tardía, la cual ya contaba tanto con el concepto de "orden" como el de "cero". Los mayas inventaron cuatro signos para el cero; los principales eran: el corte de un caracol para el cero matemático, y una flor para el cero calendárico (que implicaba no la ausencia de cantidad, sino el cumplimiento de un ciclo).
Números negativos[editar]
Brahmagupta, en el 628 de nuestra era, considera las dos raíces de las ecuaciones cuadráticas, aunque una de ellas sea negativa o irracional. De hecho en su obra es la primera vez que aparece sistematizada la aritmética (+, -, *, /, potencias y raíces) de los números positivos, negativos y el cero, que él llamaba los bienes, las deudas y la nada. Así, por ejemplo, para el cociente, establece:
Positivo dividido por positivo, o negativo dividido por negativo, es afirmativo. Cifra dividido por cifra es nada (0/0=0). Positivo dividido por negativo es negativo. Negativo dividido por afirmativo es negativo. Positivo o negativo dividido por cifra es una fracción que la tiene por denominador (a/0=¿?)
No solo utilizó los negativos en los cálculos, sino que los consideró como entidades aisladas, sin hacer referencia a la geometría. Todo esto se consiguió gracias a su despreocupación por el rigor y la fundamentación lógica, y su mezcla de lo práctico con lo formal.
Sin embargo, el tratamiento que hicieron de los negativos cayó en el vacío, y fue necesario que transcurrieran varios siglos (hasta el Renacimiento) para que fuese recuperado.
Al parecer, los chinos también poseían la idea de número negativo, y estaban acostumbrados a calcular con ellos utilizando varillas negras para los negativos y rojas para los positivos.
Transmisión del sistema indo-arábigo a Occidente[editar]
Varios autores del siglo XIII contribuyeron a esta difusión, destacan Alexandre de Villedieu (1225), Sacrobosco (circa 1195, o 1200-1256) y sobre todo Leonardo de Pisa (1180-1250). Este último, conocido como Fibonacci, viajó por Oriente y aprendió de los árabes el sistema posicional hindú. Escribió un libro, El Liber abaci, que trata en el capítulo I la numeración posicional, en los cuatro siguientes las operaciones elementales, en los capítulos VI y VII las fracciones: comunes, sexagesimales y unitarias (¡no usa los decimales, principal ventaja del sistema!), y en el capítulo XIV los radicales cuadrados y cúbicos. También contiene el problema de los conejos que da la serie: con .
No aparecen los números negativos, que tampoco consideraron los árabes, debido a la identificación de número con magnitud (¡obstáculo que duraría siglos!). A pesar de la ventaja de sus algoritmos de cálculo, se desataría por diversas causas una lucha encarnizada entre abacistas y algoristas, hasta el triunfo final de estos últimos.
Las fracciones continuas[editar]
Pietro Antonio Cataldi (1548-1626), aunque con ejemplos numéricos, desarrolla una raíz cuadrada en fracciones continuas como hoy: Queremos calcular y sea el mayor número cuyo cuadrado es menor que y , tenemos: que con su notación escribía: n=a&b/2.a.&b/2.a… Así 18=4&2/8.&2/8, que da las aproximaciones 4+(1/4), 4+(8/33)…
Siendo así los números irracionales aceptados con toda normalidad, pues se les podía aproximar fácilmente mediante números racionales.
Primera formulación de los números complejos[editar]
Los números complejos eran en pocos casos aceptados como raíces o soluciones de ecuaciones (M. Stifel (1487-1567), S. Stevin (1548-1620)) y por casi ninguno como coeficientes). Estos números se llamaron inicialmente ficticii 'ficticios' (el término "imaginario" usado actualmente es reminiscente de estas reticencias a considerarlos números respetables). A pesar de esto G. Cardano (1501-1576) conoce la regla de los signos y R. Bombelli (1526-1573) las reglas aditivas a través de haberes y débitos, pero se consideran manipulaciones formales para resolver ecuaciones, sin entidad al no provenir de la medida o el conteo.
Cardano en la resolución del problema dividir 10 en dos partes tales que su producto valga 40 obtiene como soluciones (en su notación 5p:Rm:15) y (en su notación 5m:Rm:15), soluciones que consideró meras manipulaciones «sutiles, pero inútiles».
En la resolución de ecuaciones cúbicas con la fórmula de Cardano-Tartaglia, aunque las raíces sean reales, aparecen en los pasos intermedios raíces de números negativos. En esta situación Bombelli dice en su Álgebra que tuvo lo que llamó "una idea loca", esta era que los radicales podían tener la misma relación que los radicandos y operar con ellos, tratando de eliminarlos después. En un texto posterior en 20 años utiliza p.d.m. para y m.d.m. para dando las reglas para operar con estos símbolos añadiendo que siempre que aparece una de estas expresiones aparece también su conjugada, como en las ecuaciones de 2.º grado que resuelve correctamente. Da un método para calcular .
Generalización de las fracciones decimales[editar]
Aunque se encuentra un uso más que casual de las fracciones decimales en la Arabia medieval y en la Europa renacentista, y ya en 1579 Vieta (1540-1603) proclamaba su apoyo a éstas frente a las sexagesimales, y las aceptaban los matemáticos que se dedicaban a la investigación, su uso se generalizó con la obra que Simon Stevin publicó en 1585 De Thiende (La Disme). En su definición primera dice que la Disme es una especie de aritmética que permite efectuar todas las cuentas y medidas utilizando únicamente números naturales. En las siguientes define nuestra parte entera: cualquier número que vaya el primero se dice comienzo y su signo es (0), (primera posición decimal 1/10). El siguiente se dice primera y su signo es (1) (segunda posición decimal 1/100). El siguiente se dice segunda (2). Es decir, los números decimales que escribe: 0,375 como 3(1)7(2)5(3), o 372,43 como 372(0)4(1)3(2). Añade que no se utiliza ningún número roto (fracciones), y el número de los signos, exceptuando el 0, no excede nunca a 9.
Esta notación la simplificó Joost Bürgi (1552-1632) eliminando la mención al orden de las cifras y sustituyéndolo por un «.» en la parte superior de las unidades 372·43, poco después Magini (1555-1617) usó el «.» entre las unidades y las décimas: 372.43, uso que se generalizaría al aparecer en la Constructio de Napier (1550-1617) de 1619. La «,» también fue usada a comienzos del siglo XVII por el holandés Willebrord Snellius: 372,43.
El principio de inducción matemática[editar]
Su antecedente es un método de demostración, llamado inducción completa, por aplicación reiterada de un mismo silogismo que se extiende indefinidamente y que usó Maurolyco (1494-1575) para demostrar que la suma de los primeros números naturales impares es el cuadrado del -ésimo término, es decir . Pascal (1623-1662) usó el método de inducción matemática, en su formulación abstracta, tal y como lo conocemos hoy, para probar propiedades relativas al triángulo numérico que lleva su nombre. La demostración por inducción consta siempre de dos partes: el paso base y el paso inductivo, los cuales se describen a continuación en notación moderna:
Si es un subconjunto de los números naturales (denotado por ) donde cada elemento cumple la propiedad y se tiene que:
- pertenece a .
- El hecho de que sea un miembro de implica que también lo es.
entonces , es decir que todos los números naturales tienen la propiedad .
De manera intuitiva se entiende la inducción como un efecto dominó. Suponiendo que se tiene una fila infinita de fichas de dominó, el paso base equivale a tirar la primera ficha; por otro lado, el paso inductivo equivale a demostrar que si alguna ficha se cae, entonces la ficha siguiente también se caerá. La conclusión es que se pueden tirar todas las fichas de esa fila.
La interpretación geométrica de los números complejos[editar]
Esta interpretación suele ser atribuida a Gauss (1777-1855) que hizo su tesis doctoral sobre el teorema fundamental del álgebra, enunciado por primera vez por Harriot y Girard en 1631, con intentos de demostración realizados por D’Alembert, Euler y Lagrange, demostrando que las pruebas anteriores eran falsas y dando una demostración correcta primero para el caso de coeficientes, y después de complejos. También trabajó con los números enteros complejos que adoptan la forma , con y enteros. Este símbolo para fue introducido por primera vez por Euler en 1777 y difundido por Gauss en su obra Disquisitiones arithmeticae de 1801.
La representación gráfica de los números complejos había sido descubierta ya por Caspar Wessel (1745-1818) pero pasó desapercibida, y así el plano de los números complejos se llama «plano de Gauss» a pesar de no publicar sus ideas hasta 30 años después.
Desde la época de Girard (mitad siglo XVII) se conocía que los números reales se pueden representar en correspondencia con los puntos de una recta. Al identificar ahora los complejos con los puntos del plano los matemáticos se sentirán cómodos con estos números, ver es creer.
Descubrimiento de los números trascendentes[editar]
La distinción entre números irracionales algebraicos y trascendentes data del siglo XVIII, en la época en que Euler demostró que y son irracionales y Lambert que lo es π. Los trabajos de Legendre sobre la hipótesis de que π podía no ser raíz de una ecuación algebraica con coeficientes racionales, señalaron el camino para distinguir distintos tipos de irracionales. Euler ya hacía esta distinción en 1744 pero habría que esperar casi un siglo para que se estableciera claramente la existencia de los irracionales trascendentes en los trabajos de Liouville, Hermite y Lindeman.
Liouville (1809-1882) demostró en 1844 que todos los números de la forma (p. ej., 0,101001…) son trascendentes.
Hermite (1822-1901) en una memoria Sobre la función exponencial de 1873 demostró la trascendencia de probando de una forma muy sofisticada que la ecuación: no puede existir.
Lindeman (1852-1939) en la memoria Sobre el número de 1882 prueba que el número e no puede satisfacer la ecuación: con y algebraicos, por tanto la ecuación no tiene solución para x algebraico, pero haciendo tenemos , entonces no puede ser algebraico y como i lo es entonces π es trascendente.
El problema 7 de Hilbert (1862-1943) que plantea si , con a algebraico distinto de cero y de uno, y b irracional algebraico, es trascendente fue resuelto afirmativamente por Gelfond (1906-1968) en 1934. Pero no se sabe si son trascendentes o no: ,, , … Sin embargo, e y 1/e sí que son trascendentes.
Teorías de los irracionales[editar]
Hasta mediados del siglo XIX los matemáticos se contentaban con una comprensión intuitiva de los números y sus sencillas propiedades no son establecidas lógicamente hasta el siglo XIX. La introducción del rigor en el análisis puso de manifiesto la falta de claridad y la imprecisión del sistema de los números reales, y exigía su estructuración lógica sobre bases aritméticas.
Bolzano había hecho un intento de construir los números reales basándose en sucesiones de números racionales, pero su teoría pasó desapercibida y no se publicó hasta 1962. Hamilton hizo un intento, haciendo referencia a la magnitud tiempo, a partir de particiones de números racionales:
- si ,
- cuando
- y si
- cuando
- pero no desarrolló más su teoría.
Pero en el mismo año 1872 cinco matemáticos, un francés y cuatro alemanes, publicaron sus trabajos sobre la aritmetización de los números reales:
- Charles Meray (1835-1911) en su obra Nouveau précis d’analyse infinitesimale define el número irracional como un límite de sucesiones de números racionales,[5][6] sin tener en cuenta que la existencia misma del límite presupone una definición del número real.
- Hermann Heine (1821-1881) publicó, en el Journal de Crelle en 1872, su artículo «Los elementos de la teoría de funciones», donde proponía ideas similares a las de Cantor, teoría que en conjunto se llama actualmente «teorema de Heine-Cantor».
- Richard Dedekind (1831-1916) publica su Stetigkeit und irrationale zahlen. Su idea se basa en la continuidad de la recta real y en los "agujeros" que hay si solo consideramos los números racionales. En la sección dedicada al «dominio R» enuncia un axioma por el que se establece la continuidad de la recta: «cada punto de la recta divide los puntos de ésta en dos clases tales que cada punto de la primera se encuentra a la izquierda de cada punto de la segunda clase, entonces existe un único punto que produce esta división». Esta misma idea la utiliza en la sección «creación de los números irracionales» para introducir su concepto de «cortadura». Bertrand Russell apuntaría después que es suficiente con una clase, pues esta define a la otra.
- Georg Cantor (1845-1918). Define los conceptos de: sucesión fundamental, sucesión elemental, y límite de una sucesión fundamental, y partiendo de ellos define el número real.
- Karl Weierstrass (1815-1897). No llegó a publicar su trabajo, continuación de los de Bolzano, Abel y Cauchy, pero fue conocido por sus enseñanzas en la Universidad de Berlín. Su caracterización basada en los «intervalos encajados», que pueden contraerse a un número racional pero no necesariamente lo hacen, no es tan generalizable como las anteriores, pero proporciona fácil acceso a la representación decimal de los números reales.
Álgebras hipercomplejas[editar]
La construcción de obtención de los números complejos a partir de los números reales, y su conexión con el grupo de transformaciones afines en el plano sugirió a algunos matemáticos otras generalizaciones similares conocidas como números hipercomplejos. En todas estas generalizaciones los números complejos son un subconjunto de estos nuevos sistemas numéricos, aunque estas generalizaciones tienen la estructura matemática de álgebra sobre un cuerpo, pero en ellos la operación de multiplicación no es conmutativa.
Teoría de conjuntos[editar]
La teoría de conjuntos sugirió muchas y variadas formas de extender los números naturales y los números reales de formas diferentes a como los números complejos extendían al conjunto de los números reales. El intento de capturar la idea de conjunto con un número no finito de elementos llevó a la aritmética de números transfinitos que generalizan a los naturales, pero no a los números enteros. Los números transfinitos fueron introducidos por Georg Cantor hacia 1873.
Los números hiperreales usados en el análisis no estándar generalizan a los reales pero no a los números complejos (aunque admiten una complejificación que generalizaría también a los números complejos). Aunque parece los números hiperreales no proporcionan resultados matemáticos interesantes que vayan más allá de los obtenibles en el análisis real, algunas demostraciones y pruebas matemáticas parecen más simples en el formalismo de los números hiperreales, por lo que no están exentos de importancia práctica.
Socialmente[editar]
- Los números naturales por la necesidad de contar.
- Los números fraccionarios por la necesidad de medir partes de un todo, y compartir.
- Los enteros negativos por fenómenos de doble sentido: izquierda-derecha, arriba-abajo, pérdida-ganancia.
- Los números reales por la necesidad de medir segmentos.
- Los números complejos por exigencias de resolver ecuaciones algebraicas, como el caso de la cúbicas o de x2 + 1 = 0.[7]
Sistemas de representación de los números[editar]
Cifra, dígito y numeral[editar]
Una de las formas más frecuentes de representar números por escrito consiste en un «conjunto finito de símbolos» o dígitos que, adecuadamente combinados, permiten formar cifras que funcionan como representaciones de números (cuando una secuencia específica de signos se emplea para representar un número se la llama numeral, aunque una cifra también puede representar simplemente un código identificativo).
Base numérica[editar]
Tanto las lenguas naturales como la mayor parte de sistemas de representación de números mediante cifras, usan un inventario finito de unidades para expresar una cantidad mucho mayor de números. Una manera importante de lograr eso es el uso de una base aritmética en esos sistemas un número se expresa en general mediante suma o multiplicación de números. Los sistemas puramente aritméticos recurren a bases donde cada signo recibe una interpretación diferente según su posición. Así en el siguiente numeral arábigo (base 10):
El <8> por estar en última posición representa unidades, el <6> representa decenas, el <5> centenas, el <3> millares y el <1> decenas de millares. Es decir, ese numeral representara el número:
Muchas lenguas del mundo usan una base decimal, igual que el sistema arábigo, aunque también es frecuente que las lenguas usen sistemas vigesimales (base 20). De hecho la idea de usar un número finito de dígitos o signos para representar números arbitrariamente grandes funciona para cualquier base b, donde b es un número entero mayor o igual que 2. Los ordenadores frecuentemente usan para sus operaciones la base binaria (b = 2), y para ciertos usos también se emplea la base octal (b = 8 ) o hexadecimal (b = 16). La base coincide con el número de signos primarios, si un sistema posicional tiene b símbolos primarios que designaremos por , el numeral:
Designará al número:
Números en las lenguas naturales[editar]
Las lenguas naturales usan nombres o numerales para los números frecuentemente basados en el contaje mediante dedos, razón por la cual la mayoría de las lenguas usan sistemas de numeración en base 10 (dedos de las manos) o base 20 (dedos de manos y pies), aunque también existen algunos sistemas exóticos que emplean otras bases.
Véase también[editar]
Referencias[editar]
- ↑ No hay relación de orden en el conjunto ℂ de los complejos, tal como existe en los reales, racionales, enteros y naturales
- ↑ No necesariamente. El sistema de los números reales puede ser definido axiomáticamente, tal como lo hizo David Hilbert; del mismo modo el de los números complejos, tal como lo hacen Polya (1887-1985), Alfhors (1907-1996), Markusévich (1908-1979), etc.
- ↑ Ian Stewart, Historia de las matemáticas, Crítica, 2008. ISBN 978-84-8432-369-3 p. 12-13
- ↑ Ian Stewart, Historia de las matemáticas, Crítica, 2008. ISBN 978-84-8432-369-3 p. 14
- ↑ Méray, Charles (1872). Nouveau précis d'analyse infinitésimale (en francés). Paris: F. Savy, Libraire-editeur. pp. 2-4.
- ↑ Roque, Tatiana (2011). «Les définitions les plus rigoureuses sont-elles plus faciles à comprendre ? Charles Méray et la proposition d'une définition "naturelle" des nombres irrationnels». History and Epistemology in Mathematics Education: Proceedings of the Sixth European Summer University (ESU 6) (en francés): 639-648. Consultado el 9 de julio de 2019.
- ↑ Trejo: El concepto de número
Enlaces externos[editar]
 Wikiquote alberga frases célebres de o sobre Número.
Wikiquote alberga frases célebres de o sobre Número. Wikimedia Commons alberga una galería multimedia sobre Número.
Wikimedia Commons alberga una galería multimedia sobre Número.
































































































