Conjunto numerable
En matemáticas, un conjunto numerable es un conjunto o bien finito o bien del mismo tamaño que los números naturales. Más concretamente, un conjunto se dice que es numerable (o contable) cuando es finito o cuando existe una biyección entre este conjunto y el conjunto de los números naturales.
En 1874 Georg Cantor introdujo el término conjunto numerable, contrastando conjuntos que son contables con los que son incontables. Hoy en día, los conjuntos numerables forman la base de una rama de las matemáticas llamada matemática discreta.
Definición[editar]
Un conjunto es contable si existe una función inyectiva desde números naturales ya que existe una obvia biyección entre y , no existe diferencia si se considera el 0 como natural o si no; en cualquier caso, este artículo toma la convención estándar de la lógica matemática, en donde se toma al a , es decir, a cada n de los naturales (dominio o conjunto de partida) le corresponde un elemento de S (imagen o conjunto de llegada) mediante una función .
Si la función llega a ser también sobreyectiva (y por lo tanto biyectiva), entonces se llama infinito numerable.
En otras palabras, un conjunto es infinito numerable si tiene correspondencia uno a uno con el conjunto de los números naturales .
Como se señaló anteriormente, esta terminología no es universal. Algunos autores utilizan contable en el sentido de lo que aquí se llama infinito numerable, y no incluyen los conjuntos finitos.
Formulaciones alternativas (equivalentes) de la definición en términos de una función biyectiva o una función sobreyectiva también se puede dar. Véase abajo.
Historia[editar]
En 1874, en su primer artículo de la teoría de conjuntos, Cantor demostró que el conjunto de los números reales es incontable, mostrando entonces que no todos los conjuntos infinitos son numerables.[1] En 1878 utilizó las correspondencias uno a uno para definir y comparar las cardinalidades.[2] En 1883 extendió los números naturales con sus ordinales infinitos, y usó conjuntos de ordinales para producir una infinidad de conjuntos teniendo diferentes cardinalidades infinitas.[3]
Origen del término[editar]
La noción de numerabilidad fue introducida por Georg Cantor en un artículo de 1874,[4] Sobre una propiedad del sistema de todos los números algebraicos reales[5] donde establece por una parte que el conjunto de números algebraicos reales (es decir, el conjunto de los números reales que son solución de alguna ecuación polinómica con coeficientes racionales) es numerable,[6] y por otra que el conjunto de todos los números reales no lo es, a partir de lo cual deduce inmediatamente la existencia de números trascendentes o no algebraicos, redescubriendo así un resultado de Liouville.
Su origen está ligado a la concepción del infinito en matemáticas. Hasta el descubrimiento de Cantor, el infinito era el infinito potencial, la posibilidad de continuar un proceso sin detenerse nunca. La comparación de conjuntos infinitos trae consigo la noción de infinito alcanzado, actual o completo: un conjunto infinito visto como un todo, un concepto que ha sido rechazado por numerosos matemáticos (Gauss, o, en la época de Cantor, Kronecker, etc.).[7] Para ellos, el hecho de considerar una infinidad de objetos como un todo, es decir, el concepto de conjunto infinito no tiene sentido, sino que el infinito solo puede surgir del proceso de enumeración sin repetición que nunca se detiene. Solo el infinito numerable puede tener en rigor algún sentido.
Introducción[editar]
Un conjunto es una colección de elementos, y puede ser descrito de muchas maneras. Una forma es simplemente una lista de todos sus elementos; Por ejemplo, el conjunto que consiste en los números enteros 3, 4, y 5 puede ser denotado {3, 4, 5}. Esto solo es efectivo para pequeños conjuntos, sin embargo; para conjuntos más grandes, esto podría llevar mucho tiempo y ser propenso a errores. En lugar de enumerar cada elemento, a veces se utilizan unos puntos suspensivos ("...") si el escritor cree que el lector puede adivinar fácilmente lo que falta; por ejemplo, {1, 2, 3, ..., 100} presumiblemente denota el conjunto de los enteros de 1 a 100. Incluso en este caso todavía es posible listar todos los elementos, ya que el conjunto es finito.
Algunos conjuntos son infinitos; estos conjuntos tienen más de n elementos para cualquier número entero n. Por ejemplo, el conjunto de números naturales, escrito como {0, 1, 2, 3, 4, 5, ...}, tiene un número infinito de elementos, y no podemos utilizar cualquier número normal para dar su tamaño. Sin embargo, resulta que los conjuntos infinitos tienen una idea bien definida de tamaño (o mejor dicho, de cardinalidad, que es el término técnico para el número de elementos en un conjunto), y no todos los conjuntos infinitos tienen la misma cardinalidad.

Para entender lo que esto significa, primero examinamos lo que no quiere decir. Por ejemplo, hay un número infinito de enteros impares, un número infinito de enteros pares, y (por lo tanto) un número infinito de números enteros en general. Sin embargo, resulta que el número de enteros pares, que es el mismo que el número de enteros impares, es también el mismo que el número de enteros en general. Esto se debe a que para cada entero impar, existe un homólogo, entero par: ... -2 → -4, -1 → -2, 0 → 0, 1 → 2, 2 → 4, ... En la imagen están dispuestos los números enteros y los números pares en una correspondencia uno-a-uno (o biyección), que es una función que representa dos conjuntos de tal manera que cada elemento de cada conjunto corresponde a un solo elemento en el otro conjunto.
Sin embargo, no todos los conjuntos infinitos tienen la misma cardinalidad. Por ejemplo, Georg Cantor (que introdujo este concepto) demostró que los números reales no se pueden corresponder uno-a-uno con los números naturales (enteros no negativos), y por lo tanto, el conjunto de los números reales tiene una cardinalidad mayor que el conjunto de los números naturales.
Un conjunto es numerable si: (1) es finito, o (2) si tiene la misma cardinalidad (tamaño) que el conjunto de los números naturales. De manera equivalente, un conjunto es numerable si tiene la misma cardinalidad que algún subconjunto del conjunto de los números naturales. De lo contrario, es incontable.
Formulación general sin detalles[editar]
Por definición, un conjunto S es numerable si existe una función inyectiva f : S → N desde S al conjunto de los números naturales N = {0, 1, 2, 3, ...}.
Podría parecer normal dividir los conjuntos en diferentes clases: poner todos los conjuntos que contienen un elemento juntos; todos los conjuntos que contienen dos elementos juntos; ...; por último, poner juntos todos los conjuntos infinitos y considerar que tienen el mismo tamaño. Este punto de vista no es sostenible dentro de la definición natural de tamaño.
Para elaborar esto necesitamos el concepto de biyección. Aunque una biyección parece un concepto más avanzado que un número, el desarrollo habitual de las matemáticas en términos de la teoría de conjuntos define funciones antes de los números, ya que se basan en conjuntos mucho más simples. Aquí es donde el concepto de biyección interviene: define la correspondencia
- a ↔ 1, b ↔ 2, c ↔ 3
Esto define una biyección, puesto que cada elemento de {a, b,c} se empareja con un preciso elemento de {1, 2, 3} , y viceversa.
Ahora se generaliza esta situación y definimos dos conjuntos del mismo tamaño si (y solo si) hay una biyección entre ellos. Para todos los conjuntos finitos esto nos da la definición usual de tamaño equivalente. ¿Qué nos dice sobre el tamaño de los conjuntos infinitos?
Considere los conjuntos A = {1, 2, 3, ...}, el conjunto de los enteros positivos y B = {2, 4, 6, ...}, el conjunto de los enteros positivos pares. Afirmamos que, bajo nuestra definición, estos conjuntos tienen el mismo tamaño, y que, por tanto, B es infinito numerable. Recordemos que para probar esto tenemos que probar una biyección entre ellos. Pero esto es fácil, usando n ↔ 2n , de modo que
- 1 ↔ 2, 2 ↔ 4, 3 ↔ 6, 4 ↔ 8, ....
Como en el ejemplo anterior, cada elemento de A se ha emparejado con un elemento de B y viceversa. De ahí que tengan el mismo tamaño. Este es un ejemplo de un conjunto del mismo tamaño que uno de sus subconjuntos propios (algo imposible para conjuntos finitos).
Del mismo modo, el conjunto de todos los pares ordenados de los números naturales es infinito numerable, como puede verse siguiendo una trayectoria como la de la imagen:

La representación resultante es:
- 0 ↔ (0,0), 1 ↔ (1,0), 2 ↔ (0,1), 3 ↔ (2,0), 4 ↔ (1,1), 5 ↔ (0,2), 6 ↔ (3,0) ....
Esta representación abarca a todos los pares ordenados.
Curiosamente, si trata a cada par como el numerador el y denominador de una fracción vulgar, a continuación, para cada fracción positiva, podemos llegar a una cantidad distinta que corresponderá a la misma. Esta representación incluye también a los números naturales, ya que cada número natural es también una fracción N/1. Por lo tanto podemos concluir que hay exactamente tantos números racionales positivos como números enteros positivos. Esto es cierto también para todos los números racionales, como puede verse a debajo.
Teorema: El producto cartesiano de un número finito de conjuntos numerables es numerable.
A veces más de una representación es útil. Aquí es donde se representa que el conjunto que se desea mostrar es infinito numerable en otro conjunto, y luego representa este otro conjunto de los números naturales. Por ejemplo, los números racionales positivos pueden ser fácilmente asignados a (un subconjunto de) los pares de números naturales porque p/q representa a (p, q).
¿Y qué ocurre con los subconjuntos infinitos de los conjuntos numerables infinitos? ¿Tienen éstos menos elementos que N?
Teorema: Cada subconjunto de un conjunto numerable es numerable. En particular, cada subconjunto infinito de un conjunto infinito numerable es infinito numerable.
Por ejemplo, el conjunto de los números primos es contable, mediante la asignación del n-ésimo número primo a n:
- El 2 representa al 1
- El 3 representa al 2
- El 5 representa al 3
- El 7 representa al 4
- El 11 representa al 5
- El 13 representa al 6
- El 17 representa al 7
- El 19 representa al 8
- El 23 representa al 9
- ...
¿Qué ocurre con los conjuntos que son naturalmente "mayores que" N? Por ejemplo, el conjunto de los enteros, Z, o el conjunto de los números racionales, Q, que, intuitivamente puede parecer mucho más grande que N. Pero las apariencias engañan, ya que afirmamos que:
Teorema: Z (el conjunto de todos los enteros) y Q (el conjunto de todos los números racionales) son contables.
De una manera similar, el conjunto de los números algebraicos es contable.[8]
Teorema: Cualquier unión finita de conjuntos contables es contable. Q puede definirse como el conjunto de todas las fracciones del tipo a'/b donde a y b son números enteros, con b> 0. Esto se puede corresponder con el subconjunto de triples ordenados de números naturales (a, b, c) de tal manera que si a ≥ 0 y b > 0, a y b son coprimos, y c ∈ {0, 1} luego c = 0 si a / b ≥ 0, y c = 1 en caso contrario.
- El 0 representa a (0,1,0)
- El 1 representa a (1,1,0)
- El −1 representa a (1,1,1)
- El 1/2 representa a (1,2,0)
- El −1/2 representa a (1,2,1)
- El 2 representa a (2,1,0)
- El −2 representa a (2,1,1)
- El 1/3 representa a (1,3,0)
- El −1/3 representa a (1,3,1)
- El 3 representa a (3,1,0)
- El −3 representa a (3,1,1)
- El 1/4 representa a (1,4,0)
- El −1/4 representa a (1,4,1)
- El 2/3 representa a (2,3,0)
- El −2/3 representa a (2,3,1)
- El 3/2 representa a (3,2,0)
- El −3/2 representa a (3,2,1)
- El 4 representa a (4,1,0)
- El −4 representa a (4,1,1)
- ...
Con la previsión de saber que hay conjuntos numerables, podemos preguntarnos si este último resultado puede ser ampliado. La respuesta es "sí" y "no", podemos extenderlo, pero tenemos que asumir un nuevo axioma para hacerlo.
Teorema: (Asumiendo el axioma de la elección numerable) La unión de una cantidad numerable de conjuntos numerables es numerable.
Por ejemplo, dado el conjunto numerable a, b, c, ...
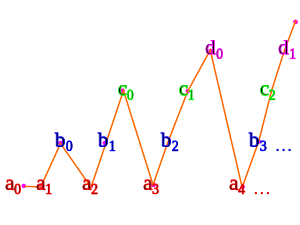
Usando una variante de la enumeración triangular vista anteriormente:
- a0 representa al 0
- a1 representa al 1
- b0 representa al 2
- a2 representa al 3
- b1 representa al 4
- c0 representa al 5
- a3 representa al 6
- b2 representa al 7
- c1 representa al 8
- d0 representa al 9
- a4 representa al 10
- ...
Tenga en cuenta que esto solo funciona si los conjuntos a, b, c, ... son conjuntos disjuntos. Si no es así, entonces la unión es aún más pequeña y por lo tanto también enumerable mediante uno de los teoremas anteriores.
También tenga en cuenta que necesitamos el axioma de la elección contable para indexar todos los conjuntos a, b, c, ... simultáneamente.
Teorema: El conjunto de todas las secuencias de longitud finita de números naturales es contable.
Este conjunto es la unión de secuencias de longitud 1, longitud 2, longitud 3, las cuales son conjuntos numerables (producto cartesiano finito). Así que estamos hablando de una unión numerable de conjuntos numerables, que es contable por el teorema anterior.
Teorema: El conjunto de todos los subconjuntos finitos de los números naturales es contable.
Teniendo un subconjunto finito, se pueden ordenar los elementos en una secuencia finita. Solo hay una cantidad numerable de secuencias finitas, por lo que también hay solo una cantidad numerable de subconjuntos finitos.
El siguiente teorema proporciona formulaciones equivalentes en términos de una función biyectiva o sobreyectiva. Una prueba de este resultado se puede encontrar en el texto de Lang.
Teorema (básico): Sea S un conjunto. Los siguientes enunciados son equivalentes:
- S es contable, es decir, existe una función inyectiva f : S → N.
- Ó S está vacío o existe una función sobreyectiva g : N → S.
- Ó S es finita o existe una biyección h : N → S.
El teorema de Cantor afirma que si A es un conjunto y P(A) es su conjunto potencia, es decir, el conjunto de todos subconjuntos de a , entonces no hay ninguna función sobreyectiva de A a P(A). Una prueba se da en el artículo del teorema de Cantor. Como consecuencia inmediata de esto y el teorema básico anterior tenemos:
Proposición: El conjunto P(N) no es contable; es decir, es incontable.
Para una elaboración de este resultado véase el argumento diagonal de Cantor.
El conjunto de los números reales es incontable (ver primera prueba de incontabilidad de Cantor), y también lo es el conjunto de todas las secuencias infinitas de los números naturales.
Algunos detalles técnicos[editar]
Las pruebas de las declaraciones contenidas en el apartado anterior se basan en la existencia de funciones con ciertas propiedades. Esta sección presenta las funciones más utilizadas en este papel, pero no la comprobación de que estas funciones tienen las propiedades requeridas. El teorema básico a menudo se utiliza para simplificar las pruebas. Observe que N en este teorema puede ser sustituido por cualquier conjunto infinito numerable.
Proposición: Cualquier conjunto finito es contable.
Prueba: Por definición, existe una biyección entre un conjunto finito no vacío, S, y el conjunto {1, 2, ..., n} para cualquier número natural positivo n. Esta función es una inyección de S en N.
Proposición: Cualquier subconjunto de un conjunto numerable es numerable.[9]
Prueba: La restricción de una función inyectiva a un subconjunto de su dominio sigue siendo inyectiva.
Proposición: Si S es un conjunto numerable y x ∉ S, entonces S ∪ {x} es numerable.[10]
Prueba: Sea f: S → N una inyección, se define g: S ∪ {x} → N como g(x) = 0 y g(y) = f(y) + 1 para toda y en S. Esta función g es una inyección.
Proposición: Si A y B son conjuntos numerables, entonces A ∪ B son numerable.[11]
Prueba: Sean f: A → N y g: B → N inyecciones, se define una nueva inyección h: A ∪ B → N como h(x) = 2f(x) si x está en A y h(x) = 2g(x) + 1 si x está en B pero no en A.
Proposición: El producto cartesiano de dos conjuntos numerables A y B es numerable.[12]
Prueba: Observe que N × N es contable por definición porque la función f : N × N → N dada por f(m, n) = 2m3n es inyectiva.[13] Entonces sigue el teorema básico del producto cartesiano, donde dos conjuntos numerables cualesquiera tienen un producto numerable. Si A y B son contables, existen subyecciones f : N → A y g : N → B. Así que
- f × g : N × N → A × B
es una subyección de un conjunto numerable N × N al conjunto A × B y el corolario implica que A × B es contable. Este resultado generaliza el producto cartesiano de cualquier colección finita de conjuntos numerables y la demostración por inducción del número de conjuntos en la colección.
Proposition: Los enteros Z son contables y los números racionales Q son contables.
Prueba: Los enteros Z son contables debido a la función f : Z → N dada por f(n) = 2n si n no es negativo f(n) = 3− n si n es negativo, es una función inyectiva. Los números racionales Q son contables debido a la función g : Z × N → Q dada por g(m, n) = m/(n + 1) es una subyección del conjunto numerable Z × N ha los racionales Q.
Proposition: Los números algebraicos A son numerables.
Prueba: Ya que todos los números algebraicos (incluyendo a los números complejos) son raíces de un polinomio. Sea un polinomio , y el número algebraico es la k-ésima raíz del polinomio (En primer lugar, ordenados por valor absoluto de menor a mayor, a continuación, ordenados por el argumento de menor a mayor). Podemos definir una función inyectiva (es decir, una a una) f : A → Q dada por , donde es el n-ésimo primo.
Proposición: Si An es un conjunto contable para cada n en N entonces la unión de todos los An es también contable.[14]
Prueba: Esto es una consecuencia del hecho de que para cada n existe una función subyectiva gn : N → An y por lo tanto la función
dada por G(n, m) = gn(m) es una subyección. Ya que N × N es numerable, el corolario implica que la unión es contable. Usamos el axioma de la elección numerable en esta prueba para escoger para cada n in N una subyección gn de la colección no vacía de subyecciones de N a An.
Una prueba topológica para la incontabilidad de los números reales se describe en la propiedad de la intersección finita.
Modelo mínimo de la teoría de conjuntos[editar]
Si hay un conjunto que es un modelo estándar (ver modelo interno) de la teoría de conjuntos de ZFC, entonces no hay un modelo estándar mínimo (ver universo constructible). El teorema de Löwenheim-Skolem se puede utilizar para demostrar que este modelo mínimo es contable. El hecho es que la noción de "incontabilidad" tiene sentido en este modelo, y en particular este modelo M contiene elementos que son:
- Subconjuntos de M, por lo tanto, contables
- Pero incontables bajo el punto de vista de M
En los primeros días de existencia, esta teoría fue considerada como una paradoja (véase paradoja de Skolem).
El modelo estándar mínimo incluye a todos los números algebraicos y a todos los números trascendentales efectivamente computables, así como a muchos otros tipos de números.
Órdenes totales[editar]
Los conjuntos numerables pueden ser ordenados totalmente de diversas maneras, por ejemplo:
- Con un buen orden (véase también número ordinal):
- El orden habitual de los números naturales (0 , 1, 2, 3, 4, 5, ...)
- Los números enteros en el orden (0, 1, 2, 3, ...; -1, -2, -3, ...)
- Otros (sin un buen orden):
- El orden habitual de números enteros (..., -3, -2, -1, 0, 1, 2, 3, ...)
- El orden habitual de los números racionales (no se puede escribir de forma explícita como una lista ordenada)
Nótese que en ambos ejemplos del buen orden, cualquier subconjunto tiene un elemento menor; y en los ejemplos de las ordenaciones sin buen orden, algunos subconjuntos no tienen un elemento menor. Esta es la definición clave que determina si una orden total es también un buen orden.
Ejemplos[editar]
|
|
- El conjunto de todos los números pares, es numerable porque la función:
es una biyección: cada número natural corresponde a un único número par y viceversa.
- El conjunto de todos los enteros también es numerable.
- Además el conjunto de todos los números racionales es numerable.[15]
- El conjunto es numerable.
- Se deriva del enunciado anterior que el conjunto de todos los racionales también es numerable, teniendo en cuenta que , donde no contiene el 0 .
- Por inducción puede probarse que son numerables para cualquier número natural k.
Véase también[editar]
- Número ordinal (teoría de conjuntos)
- Álef (cardinales)
- Contar
- Número cardinal
- Paradoja del hotel de Hilbert
- Conjunto finito
- Conjunto infinito
- Espacio compacto
- Conjunto no numerable
- Hipótesis del continuo
Notas y referencias[editar]
- ↑ Stillwell, John C. (2010), Roads to Infinity: The Mathematics of Truth and Proof, CRC Press, p. 10, ISBN 9781439865507, «El descubrimiento de Cantor de los conjuntos numerables en 1874 fue uno de los eventos más inesperados de la historia de las matemáticas. Antes de 1874, el infinito no estaba considerado un número matemático por la mayoría de la gente, de ahí la necesidad de distinguir entre contable e incontable.».
- ↑ Cantor 1878, p. 242.
- ↑ Ferreirós 2007, pp. 268, 272-273.
- ↑ y en 1873 en su correspondencia con Dedekind.
- ↑ Cantor (1874) Über eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen, Journal de Crelle 77, p258-262 (ver el centro de numeración de Göttingen [1] (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).). Disponemos del origen de esta demostración, que todavía no es la demostración más conocida que utiliza el argumento diagonal, gracias a las cartas del 7 y 9 de diciembre de 1873 de Georg Cantor a Richard Dedekind.
- ↑ Demostración de Dedekind, según su correspondencia.
- ↑ Véase por ejemplo Kneale and Kneale, The development of Logic Clarendon Press 1962, p 673.
- ↑ Kamke, 1950
- ↑ Halmos, 1960
- ↑ Avelsgaard, 1990
- ↑ Avelsgaard, 1990
- ↑ Halmos, 1960
- ↑ Avelsgaard, 1990
- ↑ Fletcher y Patty, 1988
- ↑ Se dispone en un cuadro cuya cada fila corresponde a fracciones que tienen el mismo numerador, luego se van uniendo, racionales de diferentes filas
Enlaces externos[editar]
- Esta obra contiene una traducción total derivada de «Countable set» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.






















