Cuadrilátero cíclico

En geometría euclídea, un cuadrilátero cíclico o cuadrilátero inscrito[1] es un polígono de cuatro lados cuyos vértices se encuentran sobre la misma circunferencia, denominada circunferencia circunscrita. Se dice que sus vértices son puntos cocíclicos, y el centro del círculo y su radio se denominan circuncentro y circunradio respectivamente.
Otros nombres utilizados para denominar estas figuras son cuadrilátero concíclico y cuadrilátero cordal, este último debido a que los lados del cuadrilátero son cuerdas de la circunferencia circunscrita. Por lo general, se supone que el cuadrilátero es convexo, pero también hay cuadriláteros cíclicos cruzados. Las fórmulas y propiedades dadas a continuación son válidas para el caso convexo.
La palabra cíclico tiene su origen en el griego antiguo κύκλος (kuklos) que significa "círculo" o "rueda".
Todos los triángulos poseen una circunferencia circunscrita, pero no así todos los cuadriláteros. Un ejemplo de un cuadrilátero que no puede ser cíclico es un rombo que no sea un cuadrado. En la sección caracterizaciones que figura a continuación se establece qué condición necesaria y suficiente debe satisfacer un cuadrilátero para estar inscrito en una circunferencia.
Casos especiales[editar]
Cualquier cuadrado, rectángulo, trapecio isósceles o antiparalelogramo es cíclico. Un deltoide es cíclico si y solo si posee dos ángulos rectos. Un cuadrilátero bicéntrico es un cuadrilátero cíclico que también es tangencial y un cuadrilátero ex-bicéntrico es un cuadrilátero cíclico que también es ex-tangencial. Un cuadrilátero armónico es un cuadrilátero cíclico en el que los productos de las longitudes de los lados opuestos son iguales.
Caracterizaciones[editar]
Un cuadrilátero convexo es cíclico si y solo si sus cuatro mediatrices son concurrentes en un mismo punto. Este punto común es precisamente el circuncentro.[2]
Un cuadrilátero convexo ABCD es cíclico si y solo si sus ángulos opuestos son suplementarios, es decir:[2][3]
El teorema directo fue la Proposición 22 en el Libro 3 de los Elementos de Euclides.[4] De manera equivalente, un cuadrilátero convexo es cíclico si y solo si cada ángulo interior es igual al ángulo interior opuesto.
Otra condición necesaria y suficiente para que un cuadrilátero convexo ABCD sea cíclico es que un ángulo entre un lado y una diagonal sea igual al ángulo entre el lado opuesto y la otra diagonal.[5] Es decir, por ejemplo,
Otras condiciones necesarias y suficientes para que un cuadrilátero convexo ABCD sea cíclico son:
- Que E sea el punto de intersección de las diagonales
- Que F sea el punto de intersección de las extensiones de los lados AD y BC
- Que sea un círculo cuyo diámetro sea el segmento EF, y tal que P y Q sean puntos de Pascal en los lados AB y CD formados por el círculo
- ABCD es un cuadrilátero cíclico si y solo si los puntos P y Q son colineales con el centro O del círculo
- ABCD es un cuadrilátero cíclico si y solo si los puntos P y Q son los puntos medios de los lados AB y CD[3]

El teorema de Ptolomeo expresa el producto de las longitudes de las dos diagonales e y f de un cuadrilátero cíclico como igual a la suma de los productos de lados opuestos:[6]: p.25 [3]
La proposición recíproca también es cierta. Es decir, si esta ecuación se satisface en un cuadrilátero convexo, entonces se trata de un cuadrilátero cíclico.
En un cuadrilátero convexo ABCD, tal que EFG sea el triángulo diagonal de ABCD; sea entonces la circunferencia de los nueve puntos de EFG. ABCD es cíclico si y solo si el punto de intersección de las bimedianas de ABCD pertenece al círculo de los nueve puntos de .[7][8][3]

Si dos líneas rectas, una que contiene el segmento AC y la otra que contiene el segmento BD, se cruzan en P, entonces los cuatro puntos A, B, C, D son concíclicos si y solo si[9]
La intersección P puede ser interna o externa al círculo. En el primer caso, el cuadrilátero cíclico es ABCD, y en el segundo caso, el cuadrilátero cíclico es ABDC. Cuando la intersección es interna, la igualdad establece que el producto de la longitud del segmento en el que P divide una diagonal es igual al de la otra diagonal. Esto se conoce como el teorema de las cuerdas secantes, ya que las diagonales del cuadrilátero cíclico son cuerdas de la circunferencia circunscrita.
Otra caracterización más es que un cuadrilátero convexo ABCD es cíclico si y solo si[10]
Área[editar]
El área K de un cuadrilátero cíclico con lados a, b, c y d viene dada por la fórmula de Brahmagupta[6]: p.24
donde s es el semiperímetro del cuadrilátero (s = 12(a + b + c + d)). Este es un corolario de la fórmula de Bretschneider para el cuadrilátero general, ya que los ángulos opuestos son suplementarios en el caso cíclico. Si también d = 0, el cuadrilátero cíclico se convierte en un triángulo y la fórmula se reduce a la fórmula de Herón.
El cuadrilátero cíclico tiene el área máxima entre todos los cuadriláteros que poseen la misma secuencia de longitudes laterales. Este es otro corolario de la fórmula de Bretschneider. También se puede probar usando cálculo infinitesimal.[11]
Cuatro longitudes desiguales, cada una menor que la suma de las otras tres, son los lados de cada uno de los tres cuadriláteros cíclicos no congruentes,[12] que, según la fórmula de Brahmagupta, tienen la misma área. Específicamente, para los lados a, b, c y d, el lado a podría estar opuesto a cualquiera de los lados b, c o d.
El área de un cuadrilátero cíclico con lados sucesivos a, b, c, d y ángulo B entre los lados a y b se puede expresar como[6]: p.25
o[6]: p.26
donde θ es cualquier ángulo entre las diagonales. Siempre que A no sea un ángulo recto, el área también se puede expresar como[6]: p.26
Otra fórmula es[13]: p.83
donde R es el radio de la circunferencia circunscrita. Como consecuencia directa,[14]
donde se verifica la igualdad si y solo si el cuadrilátero es un cuadrado.
Diagonales[editar]
En un cuadrilátero cíclico con vértices sucesivos A, B, C y D; y lados a = AB, b = BC, c = CD y d = DA, las longitudes de las diagonales p = AC y q = BD se pueden expresar en términos de los lados como[6] : p.25, [15][16] : p. 84
- y
mostrando el Teorema de Ptolomeo
Según el "segundo teorema de Ptolomeo",[6]: p.25, [15]
usando la misma notación que arriba.
Para la suma de las diagonales se tiene la desigualdad[17]: p.123, #2975
La igualdad se produce si y solo si las diagonales tienen la misma longitud, lo que se puede probar mediante la desigualdad de las medias aritmética y geométrica.
Por otra parte,[17]: p.64, #1639
En cualquier cuadrilátero convexo, las dos diagonales dividen el cuadrilátero en cuatro triángulos; En un cuadrilátero cíclico, los pares opuestos de estos cuatro triángulos son semejantes entre sí.
Si M y N son los puntos medios de las diagonales AC y BD, entonces[18]
donde E y F son los puntos de intersección de las extensiones de lados opuestos.
Si ABCD es un cuadrilátero cíclico donde AC se encuentra con BD en E, entonces[19]
Un conjunto de lados que pueden formar un cuadrilátero cíclico se puede organizar en cualquiera de las tres secuencias distintas, cada una de las cuales puede formar un cuadrilátero cíclico de la misma área en el mismo círculo (las áreas son las mismas de acuerdo con la fórmula del área de Brahmagupta). Cualquiera de estos dos cuadriláteros cíclicos tienen una longitud diagonal en común.[16]: p. 84
Fórmulas angulares[editar]
Para un cuadrilátero cíclico con lados sucesivos a, b, c y d; semiperímetro s; y ángulo A entre los lados a y d, las funciones trigonométricas de A están dadas por[20]
El ángulo θ entre las diagonales satisface que[6]: p.26
Si las extensiones de los lados opuestos a y c se cruzan en un ángulo φ, entonces
donde s es el semiperímetro.[6]: p.31
Fórmula del circunradio de Paramésuara[editar]
Un cuadrilátero cíclico con lados sucesivos a, b, c y d; y con semiperímetro s; tiene el circunradio (el radio del circuncírculo) dado por[15][21]
Esta fórmula fue deducida por el matemático indio Vatasseri Paramésuara en el siglo XV.
Usando la fórmula de Brahmagupta, la fórmula de Parameshvara se puede reescribir como
donde K es el área del cuadrilátero cíclico.
Anticentro y colinealidades[editar]
Los cuatro segmentos rectilíneos, cada uno perpendicular a un lado de un cuadrilátero cíclico y pasando por el punto medio del lado opuesto, son concurrentes.[22]: p.131, [23] Estos segmentos de línea se denominan m-alturas,[24] que es la abreviatura de la altura del punto medio. El punto común se llama el "anticentro". Tiene la propiedad de ser el reflejo del centro de la circunferencia circunscrita respecto al "centroide de vértices". Así, en un cuadrilátero cíclico, el circuncentro, el "centroide de vértices" y el anticentro son colineales.[23]
Si las diagonales de un cuadrilátero cíclico se cruzan en P, y los puntos medios de las diagonales son M y N, entonces el anticentro del cuadrilátero es el ortocentro del triángulo MNP.
Otras propiedades[editar]

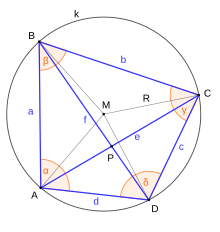
- En un cuadrilátero cíclico ABCD, los incentros M1, M2, M3 y M4 (véase la figura de la derecha) de los triángulos DAB, ABC, BCD y CDA; son los vértices de un rectángulo. Este es uno de los teoremas conocidos como teorema japonés. Los ortocentros de los mismos cuatro triángulos son los vértices de un cuadrilátero congruent a ABCD, y los centroides en esos cuatro triángulos son los vértices de otro cuadrilátero cíclico.[5]
- En un cuadrilátero cíclico ABCD con circuncentro O, sea P el punto donde se cruzan las diagonales AC y BD. Entonces, el ángulo APB es la media aritmética de los ángulos AOB y COD. Esta es una consecuencia directa del ángulo inscrito y del teorema del ángulo exterior.
- No hay cuadriláteros cíclicos con área racional y con lados racionales desiguales en progresión aritmética o en progresión geométrica.[25]
- Si un cuadrilátero cíclico tiene longitudes laterales que forman una progresión aritmética, el cuadrilátero también es ex-bicéntrico.
- Si los lados opuestos de un cuadrilátero cíclico se extienden para encontrarse en E y F, entonces las bisectrices internas de los ángulos en E y F son perpendiculares.[12]
Cuadriláteros de Brahmagupta[editar]
Un cuadrilátero de Brahmagupta[26] es un cuadrilátero cíclico con lados enteros, diagonales enteras y área entera. Todos los cuadriláteros de Brahmagupta con lados a, b, c y d; diagonales e y f; área K y circunradio R; pueden obtenerse por despeje de denominadores a partir de las siguientes expresiones que involucran parámetros racionales t, u y v:
Marco ortodiagonal[editar]
Circunradio y área[editar]
Para un cuadrilátero cíclico que también es ortodiagonal (tiene diagonales perpendiculares), supóngase que la intersección de las diagonales divide una diagonal en segmentos de longitudes p1 y p2 y divide la otra diagonal en segmentos de longitudes q1 y q2. Luego[27] (la primera igualdad es la Proposición 11 en el Libro de los Lemas de Arquímedes)
donde D es el diámetro de la circunferencia circunscrita. Esto se cumple porque las diagonales son cuerdas de la circunferencia perpendiculares entre sí. Estas ecuaciones implican que el circunradio R se puede expresar como
o, en términos de los lados del cuadrilátero, como[22]
También se deduce que[22]
Por lo tanto, de acuerdo con el teorema del cuadrilátero de Euler, el circunradio se puede expresar en términos de las diagonales p y q, y de la distancia x entre los puntos medios de las diagonales como
Una fórmula para el área K de un cuadrilátero ortodiagonal cíclico en términos de los cuatro lados se obtiene directamente al combinar el teorema de Ptolomeo y la fórmula para el área de un cuadrilátero ortodiagonal. El resultado es[28]: p.222
Otras propiedades[editar]
- En un cuadrilátero ortodiagonal cíclico, el anticentro coincide con el punto donde se cruzan las diagonales.[22]
- El teorema de Brahmagupta establece que para un cuadrilátero cíclico que también es ortodiagonal, la perpendicular desde cualquier lado a través del punto de intersección de las diagonales divide el lado opuesto.[22]
- Si un cuadrilátero cíclico también es ortodiagonal, la distancia desde la circunferencia circunscrita a cualquier lado es igual a la mitad de la longitud del lado opuesto.[22]
- En un cuadrilátero ortodiagonal cíclico, la distancia entre los puntos medios de las diagonales es igual a la distancia entre el circuncentro y el punto donde se cruzan las diagonales.[22]
Cuadriláteros esféricos cíclicos[editar]
En geometría esférica, un cuadrilátero esférico formado a partir de cuatro círculos máximos que se cruzan es cíclico si y solo si las sumas de los ángulos opuestos son iguales, es decir, α + γ = β + δ para ángulos consecutivos α, β, γ y δ del cuadrilátero.[29] I. A. Lexell comprobó en 1786 este teorema en un sentido[30] demostrando que en un cuadrilátero esférico inscrito en una circunferencia no máxima de una esfera, las sumas de ángulos opuestos son iguales, y que en el cuadrilátero circunscrito las sumas de lados opuestos son iguales. El primero de estos teoremas es el análogo esférico de un teorema del plano, y el segundo es su dual, es decir, el resultado de utilizar círculos máximos y sus polos.[31] Kiper et al.[32] demostraron el teorema recíproco: si las sumas de los lados opuestos son iguales en un cuadrilátero esférico, entonces existe una circunferencia circunscrita para este cuadrilátero.
Véase también[editar]
- Polígono cíclico
- Puntos cocíclicos
- Teorema de la mariposa
- Polígono cíclico
- Potencia de un punto
- Tabla de cuerdas de Ptolomeo
- Pentágono de Robbins
- Naraian Pandit (matemático indio, 1340-1400)
Referencias[editar]
- ↑ Levi S. Shively: «Introducción a la geometría moderna» Editorial Cecsa, México D.F., (1966)
- ↑ a b Usiskin, Zalman; Griffin, Jennifer; Witonsky, David; Willmore, Edwin (2008), «10. Cyclic quadrilaterals», The Classification of Quadrilaterals: A Study of Definition, Research in mathematics education, IAP, pp. 63-65, ISBN 978-1-59311-695-8.
- ↑ a b c d Fraivert, David; Sigler, Avi; Stupel, Moshe (2020), «Necessary and sufficient properties for a cyclic quadrilateral», International Journal of Mathematical Education in Science and Technology 51 (6): 913-938, doi:10.1080/0020739X.2019.1683772.
- ↑ Joyce, D. E. (June 1997), «Book 3, Proposition 22», Euclid's Elements, Clark University.
- ↑ a b Andreescu, Titu; Enescu, Bogdan (2004), «2.3 Cyclic quads», Mathematical Olympiad Treasures, Springer, pp. 44–46, 50, ISBN 978-0-8176-4305-8, MR 2025063.
- ↑ a b c d e f g h i Durell, C. V.; Robson, A. (2003) [1930], Advanced Trigonometry, Courier Dover, ISBN 978-0-486-43229-8.
- ↑ Fraivert, David (July 2019). «New points that belong to the nine-point circle». The Mathematical Gazette 103 (557): 222-232. doi:10.1017/mag.2019.53.
- ↑ Fraivert, David (2018). «New applications of method of complex numbers in the geometry of cyclic quadrilaterals». International Journal of Geometry 7 (1): 5-16.
- ↑ Bradley, Christopher J. (2007), The Algebra of Geometry: Cartesian, Areal and Projective Co-Ordinates, Highperception, p. 179, ISBN 978-1906338008, OCLC 213434422.
- ↑ Hajja, Mowaffaq (2008), «A condition for a circumscriptible quadrilateral to be cyclic», Forum Geometricorum 8: 103-6.
- ↑ Peter, Thomas (September 2003), «Maximizing the area of a quadrilateral», The College Mathematics Journal 34 (4): 315-6, JSTOR 3595770, doi:10.2307/3595770.
- ↑ a b Coxeter, Harold Scott MacDonald; Greitzer, Samuel L. (1967), «3.2 Cyclic Quadrangles; Brahmagupta's formula», Geometry Revisited, Mathematical Association of America, pp. 57, 60, ISBN 978-0-88385-619-2.
- ↑ Prasolov, Viktor, Problems in plane and solid geometry: v.1 Plane Geometry, archivado desde el original el 21 de septiembre de 2018, consultado el 6 de noviembre de 2011.
- ↑ Alsina, Claudi; Nelsen, Roger (2009), «4.3 Cyclic, tangential, and bicentric quadrilaterals», When Less is More: Visualizing Basic Inequalities, Mathematical Association of America, p. 64, ISBN 978-0-88385-342-9.
- ↑ a b c Alsina, Claudi; Nelsen, Roger B. (2007), «On the diagonals of a cyclic quadrilateral», Forum Geometricorum 7: 147-9.
- ↑ a b Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007 (orig. 1929).
- ↑ a b Inequalities proposed in "Crux Mathematicorum", 2007, [1].
- ↑ «ABCD is a cyclic quadrilateral. Let M, N be midpoints of diagonals AC, BD respectively...». Art of Problem Solving. 2010.
- ↑ Alexander Bogomolny, An Identity in (Cyclic) Quadrilaterals, Interactive Mathematics Miscellany and Puzzles, [2], Accessed 18 March 2014.
- ↑ Siddons, A. W.; Hughes, R. T. (1929), Trigonometry, Cambridge University Press, p. 202, OCLC 429528983.
- ↑ Hoehn, Larry (March 2000), «Circumradius of a cyclic quadrilateral», Mathematical Gazette 84 (499): 69-70, JSTOR 3621477, doi:10.2307/3621477.
- ↑ a b c d e f g Altshiller-Court, Nathan (2007) [1952], College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd edición), Courier Dover, pp. 131, 137-8, ISBN 978-0-486-45805-2, OCLC 78063045.
- ↑ a b Honsberger, Ross (1995), «4.2 Cyclic quadrilaterals», Episodes in Nineteenth and Twentieth Century Euclidean Geometry, New Mathematical Library 37, Cambridge University Press, pp. 35-39, ISBN 978-0-88385-639-0.
- ↑ Weisstein, Eric W. «Maltitude». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Buchholz, R. H.; MacDougall, J. A. (1999), «Heron quadrilaterals with sides in arithmetic or geometric progression», Bulletin of the Australian Mathematical Society 59 (2): 263-9, MR 1680787, doi:10.1017/S0004972700032883.
- ↑ Sastry, K.R.S. (2002). «Brahmagupta quadrilaterals». Forum Geometricorum 2: 167-173.
- ↑ Posamentier, Alfred S.; Salkind, Charles T. (1970), «Solutions: 4-23 Prove that the sum of the squares of the measures of the segments made by two perpendicular chords is equal to the square of the measure of the diameter of the given circle.», Challenging Problems in Geometry (2nd edición), Courier Dover, pp. 104–5, ISBN 978-0-486-69154-1.
- ↑ Josefsson, Martin (2016), «Properties of Pythagorean quadrilaterals», The Mathematical Gazette 100 (July): 213-224, doi:10.1017/mag.2016.57..
- ↑ Wimmer, Lienhard (2011). «Cyclic polygons in non-Euclidean geometry». Elemente der Mathematik 66 (2): 74-82.
- ↑ Lexell, A. J. (1786). «De proprietatibus circulorum in superficie sphaerica descriptorum». Acta Acad. Sci. Petropol. 6 (1): 58-103.
- ↑ Rosenfeld, B. A. (1988). A History of Non-Euclidean Geometry - Springer. Studies in the History of Mathematics and Physical Sciences 12. ISBN 978-1-4612-6449-1. doi:10.1007/978-1-4419-8680-1.
- ↑ Kiper, Gökhan; Söylemez, Eres (1 de mayo de 2012). «Homothetic Jitterbug-like linkages». Mechanism and Machine Theory 51: 145-158. doi:10.1016/j.mechmachtheory.2011.11.014.
Lecturas relacionadas[editar]
Enlaces externos[editar]
- Weisstein, Eric W. «Cyclic quadrilateral». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Derivación de fórmula para el área del cuadrilátero cíclico
- Incenters in Cyclic Quadrilateral en alexander Bogomolny
- Cuatro líneas concurrentes en un cuadrilátero cíclico en alexander Bogomolny
- Centro de Euler y m-alturas de un cuadrilátero cíclico en Bocetos de geometría dinámica, bocetos interactivos de geometría dinámica.




























![{\displaystyle a=[t(u+v)+(1-uv)][u+v-t(1-uv)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9cd163fbbbaa9656bd5676b09a171e5cbbb85e5b)





![{\displaystyle K=uv[2t(1-uv)-(u+v)(1-t^{2})][2(u+v)t+(1-uv)(1-t^{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/093f0b615f9b1a926b92deb5fb486cc82281c53d)






