Matriz (matemática)
En matemática, una matriz es un conjunto bidimensional de números. Dado que puede definirse tanto la suma como el producto de matrices, en mayor generalidad se dice que son elementos de un anillo. Una matriz se representa por medio de una letra mayúscula y sus elementos con la misma letra en minúscula con un doble subíndice donde el primero indica la fila y el segundo la columna a la que pertenece:
Los elementos individuales de una matriz x , se denotan a menudo por , donde el máximo valor de es , y el máximo valor de es . Siempre que la matriz tenga el mismo número de filas y de columnas que otra matriz, estas se pueden sumar o restar elemento por elemento.
Pueden sumarse, multiplicarse y descomponerse de varias formas, lo que también las hace un concepto clave en el campo del álgebra lineal.
Historia[editar]
| Año | Acontecimiento |
|---|---|
| 200 a. C. | En China los matemáticos usan series de números. |
| 1848 | J. J. Sylvester introduce el término «matriz». |
| 1858 | Cayley publica Memorias sobre la teoría de matrices. |
| 1878 | Frobenius demuestra resultados fundamentales en álgebra matricial. |
| 1925 | Heisenberg utiliza la teoría matricial en la mecánica cuántica |
El origen de las matrices es muy antiguo. Los cuadrados latinos y los cuadrados mágicos se estudiaron desde hace mucho tiempo. Un cuadrado mágico, 3 por 3, se registra en la literatura china hacia el 650 a. C.[2]
Es larga la historia del uso de las matrices para resolver ecuaciones lineales. Un importante texto matemático chino que proviene del año 300 a. C. a 200 a. C., Nueve capítulos sobre el Arte de las matemáticas (Jiu Zhang Suan Shu), es el primer ejemplo conocido de uso del método de matrices para resolver un sistema de ecuaciones simultáneas.[3] En el capítulo séptimo, "Ni mucho ni poco", el concepto de determinante apareció por primera vez, dos mil años antes de su publicación por el matemático japonés Seki Kōwa en 1683 y el matemático alemán Gottfried Leibniz en 1693.
Los «cuadrados mágicos» eran conocidos por los matemáticos árabes, posiblemente desde comienzos del s. VII d. C., quienes a su vez pudieron tomarlos de los matemáticos y astrónomos de la India, junto con otros aspectos de la matemática combinatoria. Todo esto sugiere que la idea provino de China. Los primeros «cuadrados mágicos» de orden 5 y 6 aparecieron en Bagdad en el año 983, en la Enciclopedia de la Hermandad de Pureza (Rasa'il Ihkwan al-Safa).[2]
Después del desarrollo de la teoría de determinantes por Seki Kowa y Leibniz para facilitar la resolución de ecuaciones lineales, a finales del siglo XVII, Gabriel Cramer presentó en 1750 la ahora denominada regla de Cramer. Carl Friedrich Gauss y Wilhelm Jordan desarrollaron la eliminación de Gauss-Jordan en el siglo XIX
Fue James Joseph Sylvester quien utilizó por primera vez el término «matriz» en 1848/1850.
En 1853, William Rowan Hamilton hizo algunos aportes a la teoría de matrices. Cayley introdujo en 1858 la notación matricial, como forma abreviada de escribir un sistema de m ecuaciones lineales con n incógnitas.
Cayley, Hamilton, Hermann Grassmann, Ferdinand Georg Frobenius, Olga Taussky-Todd y John von Neumann cuentan entre los matemáticos famosos que trabajaron sobre la teoría de las matrices. En 1925, Werner Heisenberg redescubre el cálculo matricial fundando una primera formulación de lo que iba a pasar a ser la mecánica cuántica. Se le considera a este respecto como uno de los padres de la mecánica cuántica.
Olga Taussky-Todd (1906-1995), durante la II Guerra Mundial, usó la teoría de matrices para investigar el fenómeno de inestabilidad aeroelastica llamado flameo.
Definición[editar]
Una matriz es un conjunto bidimensional de números (elementos de la matriz) ordenados en filas y columnas. A una matriz con filas y columnas se le denomina «matriz por » (escrito ) donde . El conjunto de las matrices de tamaño se representa como , donde es el cuerpo al cual pertenecen los elementos de la matriz.
Se dice que dos matrices son iguales si tienen el mismo tamaño (dimensión u orden) y los mismos elementos en las mismas posiciones. El elemento de una matriz que se encuentra en la fila ésima y la columna ésima se le llama elemento o elemento -ésimo de la matriz.
Dos matrices son iguales si los elementos correspondientes son iguales:
.
Para definir el concepto de matriz, el término "conjunto bidimensional" es útil, aunque poco formal, pero puede formalizarse usando el concepto de función. De este modo, una matriz de filas y columnas con entradas en un cuerpo es una función cuyo dominio es el conjunto de los pares ordenados , donde y , y cuyo codominio es . Con esta definición, la entrada es el valor de la función en el par ordenado .
Se denota a las matrices con letra mayúscula, mientras que se utiliza la correspondiente letra en minúsculas para denotar a las entradas de las mismas, con subíndices que refieren al número de fila y columna del elemento.[4] Por ejemplo, al elemento de una matriz de tamaño que se encuentra en la fila ésima y la columna ésima se le denota como , donde y .
Cuando se va a representar explícitamente una entrada la cual está indexada con un o un con dos cifras se introduce una coma entre el índice de filas y de columnas. Así por ejemplo, la entrada que está en la primera fila y la segunda columna de la matriz de tamaño se representa como mientras que la entrada que está en la fila número 23 y la columna 100 se representa como .
Además de utilizar letras mayúsculas para representar matrices, numerosos autores representan a las matrices con fuentes en negrita para distinguirlas de otros objetos matemáticos.[cita requerida] Así es una matriz, mientras que es un escalar en esa notación. Sin embargo esta notación generalmente se deja para libros y publicaciones, donde es posible hacer esta distinción tipográfica con facilidad. En otras notaciones se considera que el contexto es lo suficientemente claro como para no usar negritas.
Otra notación, en sí un abuso de notación, representa a la matriz por sus entradas, i.e. o incluso .
Como caso particular de matriz, se definen los vectores fila y los vectores columna. Un vector fila o vector renglón es cualquier matriz de tamaño mientras que un vector columna es cualquier matriz de tamaño .
A las matrices que tienen el mismo número de filas que de columnas, se les llama matrices cuadradas y el conjunto se denota
Ejemplo[editar]
Dada la matriz
es una matriz de tamaño . La entrada es 7.
La matriz
es una matriz de tamaño : un vector fila con 9 entradas.
Operaciones básicas entre matrices[editar]
Las operaciones que se pueden hacer con matrices provienen de sus aplicaciones, sobre todo de las aplicaciones en álgebra lineal. De ese modo las operaciones, o su forma muy particular de ser implementadas, no son únicas.
Suma o adición[editar]
Sean
. Se define la operación de suma o adición de matrices como una operación binaria tal que y donde en el que la operación de suma en la última expresión es la operación binaria correspondiente pero en el cuerpo . Por ejemplo, la entrada es igual a la suma de los elementos y lo cual es .
Veamos un ejemplo más explícito. Sea
No es necesario que las matrices sean cuadradas:
A la luz de estos ejemplos es inmediato ver que dos matrices se pueden sumar solamente si ambas tienen el mismo tamaño. La suma de matrices, en el caso de que las entradas estén en un cuerpo, poseen las propiedades de asociatividad, conmutatividad, existencia de elemento neutro aditivo y existencia de inverso aditivo. Esto es así ya que estas son propiedades de los cuerpos en los que están las entradas de la matriz.
- Propiedades de la suma de matrices
Sean , donde es un cuerpo entonces se cumplen las siguientes propiedades para la operación binaria
- Asociatividad
| Demostración |
| Dada la definición de la operación binaria se sigue el resultado ya que debido a que para todo . |
- Conmutatividad
| Demostración |
| Dada la definición de la operación binaria se sigue el resultado ya que debido a que para todo . |
- Existencia del elemento neutro aditivo
Existe tal que
| Demostración |
| Tómese tal que para cualquier (dónde este último es el elemento neutro aditivo en el cuerpo, el cual existe necesariamente). Entonces para cualquier se sigue que ya que para cualquier , dado que las entradas están en un cuerpo. |
- Existencia del inverso aditivo
Existe tal que
a esta matriz se le denota por .
| Demostración |
| Dada tómese tal que . Entonces ; luego, por las propiedades de cuerpo donde es el inverso aditivo de en el cuerpo para cualquier . |
En efecto, estas propiedades dependen del conjunto en el que estén las entradas, como se ha dicho antes, aunque en las aplicaciones generalmente los cuerpos usados son (los números reales) y (los números complejos).
Por como se definió la operación binaria adición se dice que esta operación es una operación interna por lo que se cumple intrínsecamente la propiedad de que es cerrado bajo adición. Con éstas propiedades se tiene que es un grupo abeliano.
En el caso en que el conjunto al que pertenecen las entradas de la matriz sea un anillo , la operación de adición de matrices continúa dotando de estructura de grupo abeliano a , ya que bajo un anillo se tiene que es un grupo abeliano. En el caso de que las entradas estén en un grupo , este necesita ser un grupo abeliano para que la adición de matrices siga dotando de estructura de grupo abeliano a .
Producto por un escalar[editar]
Sean y . Se define la operación de producto por un escalar como una función tal que y donde en donde el producto es la operación binaria correspondiente pero en el cuerpo . Por ejemplo, la entrada es igual al producto .
Veamos un ejemplo más explícito. Sea y
También es inmediato observar que el producto por un escalar da como resultado una matriz del mismo tamaño que la original. También el producto por un escalar dependerá de la estructura algebraica en la que las entradas están. En el caso de que estén en un cuerpo serán dos distributividades (una respecto de suma de matrices y otra respecto de suma en el cuerpo), asociatividad y una propiedad concerniente al producto por el elemento neutro multiplicativo del cuerpo. A continuación se presentan las propiedades.
- Propiedades del producto por un escalar
Sean y , donde es un cuerpo, entonces se cumplen las siguientes propiedades para la operación producto por un escalar
- Asociatividad
| Demostración |
| Dada la definición de la operación se sigue el resultado ya que debido a que para todo . |
- Distributividad respecto de la suma de matrices
| Demostración |
| Dada la definición de la operación se sigue el resultado ya que debido a que para todo . |
- Distributividad respecto de la suma en el cuerpo
| Demostración |
| Dada la definición de la operación se sigue el resultado ya que debido a que para todo . |
- Producto por el neutro multiplicativo del cuerpo
| Demostración |
| Dada la definición de la operación se sigue el resultado ya que debido a que para todo . |
Por como se definió la operación de producto por escalares se dice que es cerrado bajo producto por escalares. Con éstas propiedades y las de la adición se tiene que es un espacio vectorial con las operaciones de suma y producto por escalares definidas antes.
En el caso de que las entradas y los escalares no estén en un cuerpo sino en un anillo entonces no necesariamente existe el neutro multiplicativo. En caso de que exista, con lo cual el anillo es un anillo con uno, se dice que es un módulo sobre .
Ahora, a partir de las propiedades básicas se puede demostrar inmediatamente que:
| Demostración |
| Dada la definición de la operación se sigue el resultado ya que para todo |
| Demostración |
| Dada la definición de la operación se sigue el resultado ya que para todo debido a que para todo . |
| Demostración |
| Dada la definición de la operación se sigue el resultado ya que como en un cuerpo no hay divisores de cero entonces para todo implica que o para todo , i.e. . No es posible un caso en el que sólo algunas entradas de la matriz sean cero y el escalar sea no nulo ya que en esos casos estaríamos diciendo que hay divisores de cero y llegaríamos a una contradicción, ya que la suposición es que las entradas y los escalares están en un cuerpo. |
| Demostración |
| Dada la definición de la operación se sigue el resultado ya que debido a que para todo . |
Este último resultado permite usar la notación sin riesgo de ambigüedad.
Producto de matrices[editar]
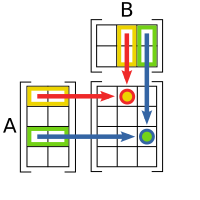
El producto de matrices se define de una manera muy peculiar y hasta caprichosa cuando no se conoce su origen. El origen proviene del papel de las matrices como representaciones de aplicaciones lineales. Así el producto de matrices, como se define, proviene de la composición de aplicaciones lineales. En este contexto, el tamaño de la matriz corresponde con las dimensiones de los espacios vectoriales entre los cuales se establece la aplicación lineal. De ese modo el producto de matrices, representa la composición de aplicaciones lineales.
En efecto, en ciertas bases tenemos que se puede representar como donde es la representación de un vector de en la base que se ha elegido para en forma de vector columna. Si tenemos dos aplicaciones lineales y entonces y , luego la aplicación se representará como donde es el producto de las representaciones matriciales de . Nótese que la composición no se puede dar entre cualquier aplicación sino entre aplicaciones que vayan de , en particular debe de haber una relación entre las dimensiones de los espacios vectoriales. Una vez dicho esto podemos definir el producto de la siguiente manera.
Sean y . Se define el producto de matrices como una función tal que y donde para toda , es decir . Por ejemplo, la entrada .
Veamos un ejemplo más explícito. Sean y
dónde la matriz producto es como habíamos establecido en la definición: una matriz .
Sin tomar en cuenta la motivación que viene desde las aplicaciones lineales, es evidente ver que si ignoramos la definición de la función de producto de matrices y solo se toma en cuenta la definición de las entradas, el producto no estará bien definido, ya que si no tiene el mismo número de columnas que de filas entonces no podremos establecer en donde acaba la suma: si la acabamos en el mayor de éstos números habrá sumandos que no están definidos ya que una de las matrices no tendrá más entradas, mientras que si tomamos el menor habrá entradas de alguna de las matrices que no se tomen en cuenta. Así es necesario que tenga el mismo número de columnas que de filas para que esté definida.
Como se puede suponer también, las propiedades de esta operación serán más limitadas en la generalidad ya que además de las limitaciones impuestas por la naturaleza de las entradas está esta limitación respecto a tamaño. Es claro, además, que el producto de matrices no siempre es una operación interna.
El producto de las matrices A x B también puede realizarse sumando el producto de cada columna de A por la correspondiente fila de B y expresarse utilizando el convenio de suma de Einstein. La enésima columna del producto de las matrices A x B es combinación lineal de las columnas de A siendo cada escalar en dicha combinación el elemento correspondiente de la enésima columna de B. La enésima fila del producto de las matrices A x B es combinación lineal de las filas de B siendo cada escalar en dicha combinación el elemento correspondiente de la enésima fila de A.
- Propiedades del producto de matrices
Sean matrices con entradas en , donde es un cuerpo, entonces se cumplen las siguientes propiedades para el producto de matrices (considerando que los productos existan)
- Asociatividad
| Demostración |
| Dada la definición de la operación se sigue el resultado ya que, si , y por lo que donde debido a que para todo . Aquí estamos considerando que es , es y es . |
- Distributividad respecto de la suma de matrices por la derecha
| Demostración |
| Dada la definición de la operación se sigue el resultado ya que debido a que para todo . Aquí estamos considerando que es , es y es . |
- Distributividad respecto de la suma de matrices por la izquierda
| Demostración |
| Dada la definición de la operación se sigue el resultado ya que debido a que para todo . Aquí estamos considerando que es , es y es . |
El producto de matrices no es conmutativo, si lo fuera la composición de funciones lineales sería conmutativa y eso en general no sucede. Obviamente, existen casos particulares de algunos tipos de matrices en los que sí hay conmutatividad. En el caso en que tengamos tendremos que el producto entre matrices en también está en . En ese caso además de espacio vectorial es un álgebra sobre un cuerpo. En el caso de que el conjunto al que pertenecen las entradas sea un anillo conmutativo con uno entonces además de módulo es un álgebra sobre un anillo. Más aún con el producto de matrices es un anillo.
Otros conceptos relacionados con matrices[editar]
Rango de una matriz[editar]
El rango de una matriz es la dimensión de la imagen de la aplicación lineal representada por , que coincide con la dimensión de los espacios vectoriales generados por las filas o columnas de .
Matriz traspuesta[editar]
La traspuesta de una matriz , donde no es necesariamente un cuerpo, es una matriz tal que . Por ejemplo la entrada .
Veamos un ejemplo más explícito. Sea
entonces su traspuesta es
Así, informalmente podríamos decir que la traspuesta es aquella matriz que se obtiene de la original cambiando filas por columnas. Las notaciones usuales para denotar la traspuesta de una matriz son .
La trasposición de matrices tiene las siguientes propiedades (donde ahora sí el conjunto de entradas debe ser al menos un anillo conmutativo):
Si representa una aplicación lineal, entonces la matriz describe la traspuesta de la aplicación lineal.
Matrices cuadradas y definiciones relacionadas[editar]
Una matriz cuadrada es una matriz que tiene el mismo número de filas que de columnas. El conjunto de todas las matrices cuadradas n-por-n junto a la suma y la multiplicación de matrices, es un anillo que generalmente no es conmutativo.
M(n,R), el anillo de las matrices cuadradas reales, es un álgebra asociativa real unitaria. M(n,C), el anillo de las matrices cuadradas complejas, es un álgebra asociativa compleja.
La matriz identidad In de orden n es la matriz n por n en la cual todos los elementos de la diagonal principal son iguales a 1 y todos los demás elementos son iguales a 0. La matriz identidad se denomina así porque satisface las ecuaciones MIn = M y InN = N para cualquier matriz M m por n y N n por k. Por ejemplo, si n = 3:
La matriz identidad es el elemento unitario en el anillo de matrices cuadradas.
Los elementos invertibles de este anillo se llaman matrices invertibles, regulares o no singulares. Una matriz A n por n es invertible si y sólo si existe una matriz B tal que AB = I
(left)
En este caso, B es la matriz inversa de A, identificada por A-1 . El conjunto de todas las matrices invertibles n por n forma un grupo (concretamente un grupo de Lie) bajo la multiplicación de matrices, el grupo lineal general.
Si λ es un número y v es un vector no nulo tal que Av = λv, entonces se dice que v es un vector propio de A y que λ es su valor propio asociado. El número λ es un valor propio de A si y sólo si A−λIn no es invertible, lo que sucede si y sólo si pA(λ) = 0, donde pA(x) es el polinomio característico de A. pA(x) es un polinomio de grado n y por lo tanto, tiene n raíces complejas múltiples raíces si se cuentan de acuerdo a su multiplicidad. Cada matriz cuadrada tiene exactamente n valores propios complejos.
El determinante de una matriz cuadrada A es el producto de sus n valores propios, pero también puede ser definida por la fórmula de Leibniz. Las matrices invertibles son precisamente las matrices cuyo determinante es distinto de cero.
El algoritmo de eliminación gaussiana puede ser usado para calcular el determinante, el rango y la inversa de una matriz y para resolver sistemas de ecuaciones lineales.
La traza de una matriz cuadrada es la suma de los elementos de la diagonal, lo que equivale a la suma de sus n valores propios.
Una matriz de Vandermonde es una matriz cuadrada cuyas filas son las potencias de un número. Su determinante es fácil de calcular.
Matriz lógica[editar]
Una matriz lógica, matriz binaria, matriz de relación, matriz booleana o matriz (0,1) es una matriz con entradas del dominio booleano . Tal matriz puede ser usada para representar una relación binaria entre un par de conjuntos finitos.
Representación de una relación matricial[editar]
Si es una relación binaria entre los finitos conjuntos ordenados e (tales que ), entonces puede representarse por la matriz lógica cuyos índices de fila y columna ordenan los elementos de e , respectivamente, tales que las entradas de se definen por:
Con el fin de designar los números de cada fila y columna de la matriz, los conjuntos X e Y están ordenados con números enteros positivos: i va desde 1 hasta la cardinalidad (tamaño) de X y j oscila entre 1 y la cardinalidad de Y.
Ejemplo[editar]
La relación binaria R en el conjunto {1, 2, 3, 4} se define de manera que aRb se lleva a cabo si y sólo si a divide b uniformemente, sin resto. Por ejemplo, 2R4 satisface la relación porque 2 divide 4 sin dejar un resto, pero 3R4 no porque cuando 3 divide 4 hay un resto de 1. El conjunto siguiente es el conjunto de pares para los que se mantiene la relación R.
- {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 4), (3, 3), (4, 4)}.
La representación correspondiente como matriz booleana es:
Algunas propiedades[editar]
La representación matricial de la relación de igualdad en un conjunto finito es la matriz de identidad, es decir, una matriz cuya diagonal principal es todo unos (1), mientras que el resto de elementos son ceros(0). Si el dominio booleano es visto como un semianillo, donde la suma corresponde al OR lógico y la multiplicación al AND lógico, la representación matricial de la composición de dos relaciones es igual al producto de la matriz de las representaciones matriciales de esta relación. Este producto se puede calcular en el tiempo esperado O(n2).
Frecuentemente, las operaciones en matrices binarias están definidas en términos de la aritmética modular mod 2, es decir, los elementos se tratan como elementos del campo de Galois GF(2) = ℤ2. Surgen una variedad de representaciones y tienen un número de formas especiales más restringidas. Se aplican por ejemplo en XOR-satisfacible (Inglés).
El número de matrices binarias mxn distintas es igual a 2mn, y es, por consiguiente, finito.
Aplicaciones[editar]
Las matrices en la computación[editar]
Las matrices son utilizadas ampliamente en la computación, por su facilidad y liviandad para manipular información. En este contexto, son una buena forma para representar grafos, y son muy utilizadas en el cálculo numérico. En la computación gráfica, las matrices son ampliamente usadas para lograr animaciones de objetos y formas.
Ejemplo de brazo robótico[editar]
El mundo de las matrices es muy amplio aunque parezca tan simple, programas como Matlab pueden crear sistemas de matrices tan complejos que incluso al programa le es difícil resolverlos. Aunque no lo parezca las matrices también se pueden aplicar al mundo de la computación y programación.
Un ejemplo sencillo sería el campo aplicado a la programación en lo que viene relacionado con la robótica ya que se utiliza en este caso el programa matlab para poder programar robots como puede ser un brazo biónico. Un ejemplo sería el Lynx6.
El Lynx6 se considera un manipulador de 5 ejes de rotación (base, hombro, codo, movimiento y rotación de la muñeca); este brazo mecánico entrega movimientos rápidos, exactos y repetitivos, gracias a los servomotores que lleva incorporados. Como paso previo se debe desarrollar una aplicación que obtiene el modelo directo FK e inverso IK del brazo robótico.

-El modelo FK consiste en encontrar una matriz de transformación homogénea T que relacione la posición cartesiana (Px, Py, PZ) y los ángulos de Euler (φ,ψ,θ) Escogiendo adecuadamente el sistema de coordenadas ligado a cada segmento es posible ir de un sistema referencial al siguiente por medio de 4 transformaciones básicas.
-Matriz de transformación (1) Donde es la matriz resultante que relaciona el sistema de referencia del segmento i-1 con el sistema de referencia del segmento ièsimo, Rotz(ϴ1) es la rotación alrededor del eje Z i-1 con un valor de ϴ1, T (0,0, di) es una traslación de una distancia di, a lo largo del eje Zi-1 , T (a1, 0,0) es una traslación de una distancia a1, a lo largo del eje Xi. Y finalmente Rotx(αi) es la rotación alrededor del eje de Xi, con un valor de αi
Los resultados van a depender exclusivamente de las características geométricas del brazo manipulador. En nuestro caso los parámetros físicos dependen de los valores de las articulaciones y longitud conocidos en cada sistema de coordenadas, deben expresarse y asignarse en términos de la convención D-H. Multiplicando las matrices individuales de la ecuación (1) en el orden correcto, la matriz de transformación, que resuelve los valores de posición y orientación en cada sistema de coordenadas es la ecuación (2) Los términos individuales de las tres primeras columnas de la matriz (n, o, a) representan la orientación del eje principal en el sistema de coordenadas. La última columna P indica la posición (x, y, z) del origen. Cada uno de los términos de la matriz pueden calcularse a partir de las ecuaciones siguientes:
La relación entre las matrices de transformación, forma la cadena cinemática de las articulaciones y segmentos consecutivos del brazo robótico. Donde T es la matriz de transformación homogénea buscada. Sustituyendo los parámetros de la tabla 2 en las matrices de transformación se obtienen estas ecuaciones. Calculando la multiplicación no conmutativa de la ecuación (17, se obtiene la matriz de transformación homogénea: Donde (n, o, a) es una terna ortogonal que representa la orientación y P es un vector (Px, Py, Pz) que representa la posición del efector extremo del brazo. La solución obtenida para una posición en reposo del brazo con Θ1= 0º , θ2= 90° , θ3 =0° , θ4= -90° y θ5=0°
Teoría de matrices[editar]
La teoría de matrices es una rama de las matemáticas que se centra en el estudio de matrices. Inicialmente una rama secundaria del álgebra lineal, ha venido cubriendo también los temas relacionados con la teoría de grafos, el álgebra, la combinatoria y la estadística.
Matrices relacionadas con otros temas[editar]
Una matriz puede identificarse a una aplicación lineal entre dos espacios vectoriales de dimensión finita. Así la teoría de las matrices habitualmente se considera como una rama del álgebra lineal. Las matrices cuadradas desempeñan un papel particular, porque el conjunto de matrices de orden n (n entero natural no nulo dado) posee propiedades de « estabilidad » de operaciones.
Los conceptos de matriz estocástica y matriz doblemente estocástica son herramientas importantes para estudiar los procesos estocásticos, en probabilidad y en estadística.
Las matrices definidas positivas aparecen en la búsqueda de máximos y mínimos de funciones a valores reales, y a varias variables.
Es también importante disponer de una teoría de matrices a coeficientes en un anillo. En particular, las matrices a coeficientes en el anillo de polinomios se utilizan en teoría de mandos.
En matemáticas puras, los anillos de matrices pueden proporcionar un rico campo de contraejemplos para conjeturas matemáticas.
Matrices en teoría de grafos[editar]
En teoría de los grafos, a todo grafo etiquetado corresponde la matriz de adyacencia. Una matriz de permutación es una matriz que representa una permutación; matriz cuadrada cuyos coeficientes son 0 o 1, con un solo 1 en cada línea y cada columna. Estas matrices se utilizan en combinatorio.
También existe otro tipo de matriz además de la matriz de adyacencia que es la conocida como matriz de incidencia en la cual el grafo se muestra en una matriz de A (serían las aristas) por V (serían los vértices), donde contiene la información de la arista (1 si está conectado y 0 no conectado).
Si nos dan un grafo , de orden , podemos llegar a representar una relación de adyacencia, mediante una matriz nxn, también llamada matriz de adyacencia de G.
Se deben de tener en cuenta una serie de observaciones sobre esto:
- La matriz de adyacencia es una matriz booleana, como se ha dicho antes es una matriz que solo puede contener 0 y 1.
- Σi xij = semigrado exterior de xi
- Σj xij = semigrado interior de xj
En la teoría de grafos, se llama matriz de un grafo a la matriz que indica en la línea i y la columna j el número de aristas que enlazan el vértice i al vértice j. En un grafo no orientado, la matriz es simétrica. La suma de los elementos de una columna permite determinar el grado de un vértice. La matriz indica en la línea i y la columna j el número de caminos a n aristas que adjuntan el vértice i al vértice j.

A continuación mostraremos un ejemplo de un grafo y su matriz de adyacencia:
La matriz de adyacencia de este grafo vendría dada de la forma:
| / | V1 | V2 | V3 | V4 | V5 |
|---|---|---|---|---|---|
| V1 | 0 | 1 | 0 | 0 | 0 |
| V2 | 1 | 0 | 1 | 1 | 0 |
| V3 | 1 | 1 | 0 | 1 | 0 |
| V4 | 0 | 1 | 1 | 1 | 0 |
| V5 | 0 | 0 | 1 | 0 | 0 |
La matriz de adyacencia se basa en las conexiones que se realizan entre los vértices del grafo apareciendo así un 1 en los casos en los que dos vértices están conectados y un 0 en los casos en los que no.
En algunos casos como el de la posición V3/V5 se observa un 0 debido a que la conexión entre ellos muestra un sentido permitiendo el paso de flujo de V5 a V3 pero no al contrario, motivo por el cual V5/V3 si presenta un 1.
Cabe decir que si se toma otra ordenación de los vértices la matriz de adyacencia será diferente, pero todas las matrices de adyacencia resultantes de un mismo grafo están unidas por una matriz de permutación P tal que P-1 C P = A (Siendo C y A dos matrices de adyacencia distintas pero provenientes de un mismo grafo).
Análisis y geometría[editar]
Sea una función diferenciable, siendo sus las componentes escalares. Se define la matriz jacobiana de como:
Si n > m, y si el rango de la matriz Jacobi alcanza su valor máximo m, f es localmente invertible en ese punto, por el teorema de la función implícita. Las ecuaciones diferenciales parciales pueden clasificarse considerando la matriz de coeficientes de los operadores diferenciales de orden más alto de la ecuación. Para las ecuaciones diferenciales elípticas parciales esta matriz es positiva para todos sus valores, los cuales tienen una influencia decisiva en el grupo de soluciones posibles de la ecuación en cuestión.
La matriz hessiana de una función consiste en la segunda derivada de f con respecto a las varias direcciones de coordenadas, esto es,
Codifica información sobre el comportamiento creciente de la función: dando un punto crítico x = (x1, ..., xn), esto es, un punto donde la primera derivada parcial de ƒ desaparece, la función tiene un mínimo local si la matriz de Hessian es definida positiva para todos sus valores. La programación cuadrática puede usarse para encontrar mínimos y máximos globales de una función cuadrática estrechamente relacionadas con las asociadas a matrices.
El método de elementos finitos es un importante método numérico para resolver ecuaciones diferenciales parciales, extensamente aplicado en simulaciones de sistemas físicos complejos. Intenta aproximar la solución a alguna ecuación de funciones lineales pieza a pieza, donde las piezas son elegidas con respecto a una rejilla suficientemente fina, que a su vez puede ser refundida como una ecuación matricial.
Algunos teoremas[editar]
Véase también[editar]
- Cálculo de matrices
- Descomposición de Schur
- Descomposición en valores singulares
- Descomposición QR
- Determinante (matemática)
- Eliminación de Gauss-Jordan
- Factorización LU
- Forma canónica de Jordan
- Lema de Schur
- Matlab
- Matriz triangular
Referencias[editar]
- Beezer, Rob, Un primer curso en álgebra lineal, licencia bajo GFDL. (En inglés)
- Jim Hefferon: Álgebra lineal (Libros de texto en línea) (En inglés)
Notas[editar]
- ↑ Tony Crilly (2011). 50 cosas que hay que saber sobre matemáticas. Ed. Ariel. ISBN 978-987-1496-09-9.
- ↑ a b Swaney, Mark. History of Magic Squares.
- ↑ Shen Kangshen et al. (ed.) (1999). Nine Chapters of the Mathematical Art, Companion and Commentary. Oxford University Press. cited byOtto Bretscher (2005). Linear Algebra with Applications (3rd ed. edición). Prentice-Hall. pp. 1.
- ↑ De Burgos, Juan (2006). «Sistemas de ecuaciones lineales». Álgebra lineal y geometría cartesiana. p. 6. ISBN 9788448149000.
Enlaces externos[editar]
- Determinante de una matriz
- Una breve historia del álgebra lineal y de la teoría de matrices lineal (en inglés)
- Matemáticas/Matrices(En Wikilibros)
- Esta obra contiene una traducción parcial derivada de «Matrix (mathematics)» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
- Esta obra contiene una traducción parcial derivada de «Logical Matrix» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.














































































































































































![{\displaystyle A=[a_{ij}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1abea4bedfb4eabb36df6d0c0b97aebc10829fb)







