Permutación

Cada una de las seis filas es una permutación diferente de tres bolas distintas.

En matemáticas, una permutación de un conjunto es, en términos generales, una disposición de sus miembros en una secuencia u orden lineal, o si el conjunto ya está ordenado, una variación del orden o posición de los elementos de un conjunto ordenado o una tupla. La palabra "permutación" también se refiere al acto o proceso de cambiar el orden lineal de un conjunto ordenado.​

Las permutaciones difieren de las combinaciones, que son selecciones de algunos miembros de un conjunto sin importar el orden. Por ejemplo, escritas como tuplas, hay seis permutaciones del conjunto {1, 2, 3}, a saber (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2) y (3, 2, 1). Estas son todas las ordenaciones posibles de este conjunto de tres elementos. Los anagramas de palabras cuyas letras son diferentes también son permutaciones: las letras ya están ordenadas en la palabra original, y el anagrama es una reordenación de las letras. El estudio de las permutaciones de conjuntos finitos es un tema importante en los campos de la combinatoria y la teoría de grupos.

Las permutaciones se utilizan en casi todas las ramas de las matemáticas y en muchos otros campos de la ciencia. En informática, se utilizan para analizar algoritmos de ordenación; en física cuántica, para describir estados de partículas; y en biología, para describir secuencias de ARN.

El número de permutaciones de n objetos distintos es n factorial, normalmente escrito como n!, que significa el producto de todos los enteros positivos menores o iguales a n.

Técnicamente, una permutación de un set S se define como una biyección de S a sí mismo.​​ Es decir, es una función de S a S para la cual cada elemento ocurre exactamente una vez como un valor de imagen. Esto está relacionado con el reordenamiento de los elementos de S en el que cada elemento s es reemplazado por el correspondiente f(s). Por ejemplo, la permutación (3, 1, 2) mencionada anteriormente es descrita por la función $\alpha$ definida como

$\alpha (1)=3,\quad \alpha (2)=1,\quad \alpha (3)=2$.

El conjunto de todas las permutaciones de un conjunto forman un grupo llamado grupo simétrico del conjunto. La operación de grupo es la composición (realizar dos reordenamientos dados sucesivamente), que da como resultado otro reordenamiento. Como las propiedades de las permutaciones no dependen de la naturaleza de los elementos del conjunto, suelen ser las permutaciones del conjunto $\{1,2,\ldots ,n\}$ las que se consideran para estudiar las permutaciones.

En combinatoria elemental, las k-permutaciones, o permutaciones parciales, son los arreglos ordenados de k elementos distintos seleccionados de un conjunto. Cuando k es igual al tamaño del conjunto, son las permutaciones del conjunto.

Definición formal

La definición intuitiva de permutación, como un ordenamiento de los elementos de un conjunto se formaliza con el uso del lenguaje de funciones matemáticas.

Una permutación de un conjunto X es una función biyectiva de dicho conjunto en sí mismo.

Ejemplos:

1. En el caso de un elemento (1) solo hay una posible permutación: $(1)$.

${\begin{matrix}A&\xrightarrow {Identidad} &A\\1&\longmapsto &1\\\end{matrix}}$

2. En el caso de dos elementos {1,2} solo hay dos posibles permutaciones (ordenamientos o posiciones de cada elemento): $(1,\,2)$ y $(2,\,1)$.

${\begin{matrix}A&\xrightarrow {Identidad} &A\\1&\longmapsto &1\\2&\longmapsto &2\\\end{matrix}}$, ${\begin{matrix}A&\xrightarrow {(2,\,1)} &A\\1&\longmapsto &2\\2&\longmapsto &1\\\end{matrix}}$

3. En el caso de tres elementos {1, 2, 3} cada permutación diferente sobre el conjunto {1, 2, 3} equivale a una forma de ordenar los elementos.

${\begin{matrix}A&\xrightarrow {Identidad} &A\\1&\longmapsto &1\\2&\longmapsto &2\\3&\longmapsto &3\\\end{matrix}}$, ${\begin{matrix}A&\xrightarrow {(2,\,1,\,3)} &A\\1&\longmapsto &2\\2&\longmapsto &1\\3&\longmapsto &3\\\end{matrix}}$, ${\begin{matrix}A&\xrightarrow {(3,\,2,\,1)} &A\\1&\longmapsto &3\\2&\longmapsto &2\\3&\longmapsto &1\\\end{matrix}}$, ${\begin{matrix}A&\xrightarrow {(1,\,3,\,2)} &A\\1&\longmapsto &1\\2&\longmapsto &3\\3&\longmapsto &2\\\end{matrix}}$, ${\begin{matrix}A&\xrightarrow {(2,\,3,\,1)} &A\\1&\longmapsto &2\\2&\longmapsto &3\\3&\longmapsto &1\\\end{matrix}}$, ${\begin{matrix}A&\xrightarrow {(3,\,1,\,2)} &A\\1&\longmapsto &3\\2&\longmapsto &1\\3&\longmapsto &2\\\end{matrix}}$

En la definición de permutación, no se establece condición alguna sobre X, el cual puede incluso ser infinito. Sin embargo, es común considerar únicamente el caso en que X es un conjunto finito al estudiar permutaciones.

En combinatoria

La combinatoria trata del número de diferentes maneras que existen de considerar conjuntos formados a partir de elementos de un conjunto dado, respetando ciertas reglas, como el tamaño, el orden, la repetición, la partición. Así un problema combinatorio consiste usualmente en establecer una regla sobre cómo deben ser las agrupaciones y determinar cuántas existen que cumplan dicha regla. Básicamente, tres asuntos: permutaciones, combinaciones y variaciones.

Un tipo importante de esas agrupaciones son las llamadas permutaciones. Dada una n-tupla ordenada de los elementos de un conjunto, el número de permutaciones es el número de n-tuplas ordenadas posibles.

Fórmula del número de permutaciones

Dado un conjunto finito $A\,\!$ de $n\,\!$ elementos, el número de todas sus permutaciones es igual a factorial de n:
$n!=n(n-1)(n-2)\cdots 1\,\!$.

Demostración: Dado que hay $n\,\!$ formas de escoger el primer elemento y, una vez escogido este, solo tenemos $(n-1)\,\!$ formas de escoger el segundo elemento, y así sucesivamente, vemos que cuando llegamos al elemento k-ésimo solo tenemos $[n-(k-1)]\,\!$ posibles elementos para escoger, lo que nos lleva a que tenemos $n(n-1)(n-2)\cdots 2\cdot 1\,\!$ formas de ordenar el conjunto, justamente lo que enunciamos anteriormente.

Ejemplo: sea el conjunto A={1,2,3} en este caso hay 6 permutaciones, en forma compacta: 123, 132, 213, 231, 312, 321. En álgebra, para estudiar los grupos simétricos se presentan entre paréntesis y en dos filas, en la primera siempre aparece 1 2 3.

Otro ejemplo de lo mismo: si se va a formar un comité que involucra presidente, tesorero y secretario, habiendo tres candidatos a, b, c ; cuando se elige por sorteo los cargos sucesivamente, hay seis posibilidades u ordenaciones: abc, acb, bac, bca, cab, cba.

En teoría de grupos

Notaciones

Representación gráfica de la permutación $\sigma$ que revela su estructura compuesta por 2 ciclos de longitud 4.

La primera forma de escribir una permutación $\sigma$, aunque no es la más compacta, consiste en escribirla en forma de matriz de dos filas, situando en la primera los elementos ordenados del dominio 1, 2, 3,...,n, y en la segunda fila las imágenes correspondientes a los elementos reordenados $\sigma (1),\,\sigma (2),\,\sigma (3),\,\dots ,\,\sigma (n).$

Por ejemplo, dado el conjunto ordenado $\{1,...,8\}$ podemos expresar una permutación $\sigma$ sobre éste mediante una matriz de correspondencias:

$\sigma ={\begin{pmatrix}1&2&3&4&5&6&7&8\\3&4&5&7&6&1&8&2\end{pmatrix}}$

Por ser biyectiva por definición, podemos encontrar una aplicación inversa $\sigma ^{-1}$ de forma que su composición genera la aplicación identidad. Para ello, en primer lugar intercambiamos las filas y finalmente reordenamos las columnas de modo que los elementos del dominio queden ordenados de forma natural:

$\sigma ^{-1}$ $={\begin{pmatrix}3&4&5&7&6&1&8&2\\1&2&3&4&5&6&7&8\end{pmatrix}}$ $={\begin{pmatrix}1&2&3&4&5&6&7&8\\6&8&1&2&3&5&4&7\end{pmatrix}}$

Notación de ciclos

Existe otra notación más compacta, llamada notación de ciclos. Un ciclo es una permutación que intercambia cíclicamente elementos y fija los restantes. Esta notación revela mejor la estructura interna de la permutación. Para ello:

1. Empezamos con cualquier elemento. Lo escribimos, a su derecha escribimos su imagen, a la derecha de esta, la imagen de su imagen, y seguimos así hasta que se complete un ciclo.
2. Luego cogemos cualquier elemento no contenido en el primer ciclo, volvemos a escribir su imagen a su derecha, y continuamos hasta completar el segundo ciclo.
3. El proceso continúa hasta que la permutación entera ha quedado descrita como producto de ciclos disjuntos.

Siguiendo con el mismo ejemplo de antes, en notación de ciclos, $\sigma$ quedaría expresada como composición de dos ciclos:

$\sigma =(1356)(2478)$.

Un ciclo de longitud k es llamado k-ciclo.

Descomposición de una permutación en ciclos disjuntos

La descomposición realizada por el procedimiento anterior no es única en principio, pues podrían haberse obtenido cualquiera de estos resultados equivalentes:

$\sigma =(1356)(2478)=(2478)(1356)=(8247)(6135)=(3561)(4782)=(5613)(7824)=(6135)(8247)$

La descomposición canónica de una permutación como producto de ciclos se obtiene en dos pasos (según Miklós Bóna):

• Dentro de cada ciclo, se escribe primero el elemento más grande;
• A continuación, ordenamos los ciclos en orden creciente en base al primer elemento de cada ciclo.

Frecuentemente, suelen omitirse los ciclos de longitud 1. Así la permutación (1 3)(2)(4 5) se escribe simplemente como (3 1)(5 4) en forma canónica.

Richard P. Stanley llama «representación estándar» a esta forma​, mientras que Martin Aigner usa el término «forma estándar»​. Sergey Kitaev también usa el término «forma estándar» pero invierte los criterios: en cada ciclo se lista primero el elemento más pequeño y luego los ciclos se ordenan de mayor a menor según el primer elemento​.

Como curiosidad, la forma canónica permite eliminar los paréntesis sin que haya pérdida de información, o bien recuperar la posición de los paréntesis a partir de un listado de elementos sin ellos. Por ejemplo, usando los criterios de Miklós Bóna, en una forma canónica que haya «perdido» los paréntesis, como 3 1 2 5 4 6, el primer ciclo estará formado por el primer elemento de la lista, 3, y los siguientes que sean menores que él: (3 1 2). El siguiente elemento mayor que el primero (5 > 3) inicia un nuevo ciclo, junto con los siguientes menores que él, y así sucesivamente. Por lo tanto, la forma canónica ha de ser (3 1 2) (5 4) (6).

Descomposición de una permutación en transposiciones

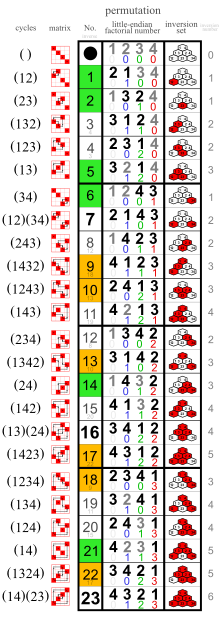
Permutaciones de 4 elementos

De izquierda a derecha aparecen las permutaciones en forma matricial, en forma de vector y como producto de transposiciones. Los números a la derecha indican la cantidad de transposiciones con que se puede escribir cada permutación (este número no es único, pero sí su paridad). Las permutaciones impares están marcadas con verde o naranja.

Una transposición es una permutación que intercambia dos elementos y fija los restantes. Dicho de otro modo, es un ciclo de longitud 2. Una propiedad interesante es que cualquier permutación se puede construir como una composición de transposiciones, aunque no de manera única. Dadas dos descomposiciones en transposiciones de una permutación se cumple que ambas usaran un número par o ambas usarán un número impar, eso permite definir de manera unívoca la signatura de una permutación.

Las transposiciones permiten descomponer una permutación cualquiera de una forma diferente a la descomposición en ciclos. En particular, las transposiciones que aparezcan no tendrán que ser disjuntas: Por ejemplo, el ciclo (1 2 3 4) = (1 2) (2 3) (3 4).

Nótese la diferencia entre permutación, ciclo y transposición, dado lo similar de la notación, la expresión anterior es equivalente a:

${\begin{pmatrix}1&2&3&4\\2&3&4&1\end{pmatrix}}={\begin{pmatrix}1&2&3&4\\2&1&3&4\end{pmatrix}}\circ {\begin{pmatrix}1&2&3&4\\2&3&4&1\end{pmatrix}}\circ {\begin{pmatrix}1&2&3&4\\1&3&2&4\end{pmatrix}}\circ {\begin{pmatrix}1&2&3&4\\1&2&4&3\end{pmatrix}}$

La composición señalada como: $\circ$ se opera de derecha a izquierda y no es conmutativa.

Aquí el orden de aplicación es importante: en primer lugar (3 4) deja el 4 en su sitio definitivo y el 3 descolocado. Después (2 3) deja en su sitio definitivo el 3 y el 2 descolocado, que quedará recolocado definitivamente por (1 2).

Para ver que cualquier permutación se descompone como producto de transposiciones bastará ver que todo ciclo lo hace. La descomposición no es única. Por ejemplo:

$(a_{1},\ldots ,a_{n})=$

$(a_{1},a_{2})(a_{2},a_{3})\cdots (a_{n-1},a_{n})=(a_{1},a_{n})(a_{1},a_{n-1})\cdots (a_{1},a_{2}).$

El número de transposiciones de la descomposición tampoco es único. Por ejemplo:

$(a_{1},\ldots ,a_{n})=$

$(a_{n-1},a_{n})(a_{1},a_{n-1})(a_{n-1},a_{n})(a_{1},a_{n-1})(a_{1},a_{n-2})\cdots (a_{1},a_{2}).$

Pero la paridad del número de transposiciones de la descomposición sí está determinada. Es decir, para cualquier par de descomposiciones distintas de $\sigma$ con n y con m transposiciones, respectivamente, n y m tienen la misma paridad (serán simultáneamente pares o impares).

Dada una permutación cualquiera, se define el siguiente homomorfismo de grupos:

$\varepsilon :S_{n}\to (\{-1,1\},\cdot )\approx (\mathbb {Z} _{2},+),\qquad \varepsilon (\sigma )=(-1)^{m},$

donde $\scriptstyle S_{n}$ es el grupo simétrico de n elementos y m es un número entero, tal que existen transposiciones $\scriptstyle \tau _{i}$ tales que:

$\sigma =\tau _{1}\tau _{2}\dots \tau _{m}\in S_{n}.$

Permutación par y permutación impar

Llamaremos permutación par (resp. impar) a la que se escribe como composición de un número par (resp. impar) de transposiciones.

Como ejemplo, dado el conjunto {1, 2, 3} de las 6=3! permutaciones posibles:

Permutación 1

La permutación

${\begin{pmatrix}1&2&3\\1&2&3\end{pmatrix}}$

Escritas en notación de ciclos:

$(1)(2)(3)\equiv id$

Las transposiciones: La identidad no tiene transposiciones. El número de transposiciones de id es 0(cero).

Permutación 2

La permutación

${\begin{pmatrix}1&2&3\\1&3&2\end{pmatrix}}$

Escritas en notación de ciclos:

$(1)(23)\equiv (23)$

Las transposiciones:

$(23)\,$

El número de transposiciones es :1.

Permutación 3

La permutación

${\begin{pmatrix}1&2&3\\2&1&3\end{pmatrix}}$

Escritas en notación de ciclos:

$(12)(3)\equiv (12)$

Las transposiciones:

$(12)\,$

El número de transposiciones es :1.

Permutación 4

La permutación

${\begin{pmatrix}1&2&3\\2&3&1\end{pmatrix}}$

Escritas en notación de ciclos:

$(123)\,$

Las transposiciones:

$(12)(23)\,$

El número de transposiciones es :2.

Permutación 5

La permutación

${\begin{pmatrix}1&2&3\\3&1&2\end{pmatrix}}$

Escritas en notación de ciclos:

$(132)\,$

Las transposiciones:

$(13)(32)\,$

El número de transposiciones es :2.

Permutación 6

La permutación

${\begin{pmatrix}1&2&3\\3&2&1\end{pmatrix}}$

Escritas en notación de ciclos:

$(13)(2)\equiv (13)$

Las transposiciones: La transposición es:

$(13)\,$

El número de transposiciones es :1.

Conclusión

En general, se demuestra que la mitad de las n! permutaciones de un conjunto de n elementos son pares y la otra mitad impares. Esto surge como consecuencia directa de la existencia del morfismo $\varepsilon :S_{n}\to (\{-1,1\},\cdot )$ que tiene como núcleo justamente a las permutaciones pares.

Estructura de grupo

Dado un número natural $n\geq 1$, consideramos el conjunto $X=\{1,2,...,n\}$. Definimos el grupo de permutaciones de $n$ elementos, que denotaremos por $S_{n}$, o lo que es lo mismo, el conjunto de aplicaciones biyectivas de $X$ a $X$.

Las permutaciones pares forman un subgrupo normal de índice 2 del grupo S_n, al que llamaremos grupo alternado, y notaremos por $A_{n}$.

Desorden

Permutación completa o desorden es una permutación de objetos en la que ninguno de los elementos aparece en su lugar natural.

Por ejemplo: la permutación 23451 es un desorden o permutación completa de un 12345 ya que ninguna cifra se encuentra en su posición original. Pero si la permutación fuera 15423 no se consideraría un desorden, debido a que el número 1 se encuentra en su posición natural.

• Teorema

El número de permutaciones completas de un conjunto de $n$ elementos es:

$PC_{n}=n!\left(1-{1 \over 1!}+{1 \over 2!}-{1 \over 3!}+...+(-1)^{n}{1 \over n!}\right)$

Se puede demostrar utilizando el principio de inclusión-exclusión.

Dato histórico

El estudio de las permutaciones de las raíces de ecuaciones algebraicas le permitió a Galois elaborar los inicios de la teoría de grupos y usar este vocablo, por primera vez, en matemáticas. Y empezó por los grupos no abelianos.

El concepto de permutación aparece en la obra hebrea Séfer Yetzirah ('El libro de la creación'), un manuscrito elaborado por un místico entre el año 200 y el 600. Pero existía ya un resultado anterior de Jenócrates de Calcedonia (396-314 a. C.)​

Véase también

• Ciclo (permutación)
• Matriz permutación
• Combinatoria
• Combinaciones
• Variaciones

Bibliografía

• Bogart, Kenneth P. (1990), Introductory Combinatorics (2nd edición), Harcourt Brace Jovanovich, ISBN 978-0-15-541576-8 .
• Bóna, Miklós (2004), Combinatorics of Permutations, Chapman Hall-CRC, ISBN 978-1-58488-434-7 .
• Bona, Miklos (2012), Combinatorics of Permutations (2nd edición), CRC Press, ISBN 978-1-4398-5051-0 .
• Brualdi, Richard A. (2010), Introductory Combinatorics (5th edición), Prentice-Hall, ISBN 978-0-13-602040-0 .
• Cameron, Peter J. (1994), Combinatorics: Topics, Techniques, Algorithms, Cambridge University Press, ISBN 978-0-521-45761-3 .
• Carmichael, Robert D. (1956), Introduction to the theory of Groups of Finite Order, Dover, ISBN 978-0-486-60300-1 .
• Fraleigh, John B. (1976), A First Course In Abstract Algebra (2nd edición), Reading: Addison-Wesley, ISBN 0-201-01984-1 .
• Gerstein, Larry J. (1987), Discrete Mathematics and Algebraic Structures, W.H. Freeman and Co., ISBN 978-0-7167-1804-8, (requiere registro) .
• Hall, Marshall, Jr. (1959), The Theory of Groups, MacMillan .
• Humphreys, J. F. (1996), A course in group theory, Oxford University Press, ISBN 978-0-19-853459-4 .
• Knuth, Donald (1973), Sorting and Searching, The Art of Computer Programming 3 . This book mentions the Lehmer code (without using that name) as a variant C₁,...,C_n of inversion tables in exercise 5.1.1–7 (p. 19), together with two other variants.
• Knuth, Donald (2005), Generating All Tuples and Permutations, The Art of Computer Programming 4, Addison–Wesley, ISBN 978-0-201-85393-3 . Fascicle 2, first printing.
• McCoy, Neal H. (1968), Introduction To Modern Algebra, Revised Edition, Boston: Allyn and Bacon, LCCN 68015225 .
• Nering, Evar D. (1970), Linear Algebra and Matrix Theory (2nd edición), New York: Wiley, LCCN 76091646 .
• Rotman, Joseph J. (2002), Advanced Modern Algebra, Prentice-Hall, ISBN 978-0-13-087868-7 .
• Stedman, Fabian (1677), Campanalogia, London . The publisher is given as "W.S." who may have been William Smith, possibly acting as agent for the Society of College Youths, to which society the "Dedicatory" is addressed. In quotations the original long "S" has been replaced by a modern short "s".
• Webster's Seventh New Collegiate Dictionary, Springfield: G. & C. Merriam Company, 1969 .

• Datos: Q161519
• Multimedia: Permutations / Q161519