Cristalografía de rayos X

La cristalografía de rayos X es una técnica experimental para el estudio y análisis de materiales, basada en el fenómeno de difracción de los rayos X por sólidos en estado cristalino.
Los rayos X son difractados por los electrones que rodean los átomos por ser su longitud de onda del mismo orden de magnitud que el radio atómico. El haz de rayos X emergente tras esta interacción contiene información sobre la posición y tipo de átomos encontrados en su camino. Los cristales, gracias a su estructura periódica, dispersan elásticamente los haces de rayos X en ciertas direcciones y los amplifican por interferencia constructiva, originando un patrón de difracción.[n. 1] Existen varios tipos de detectores especiales para observar y medir la intensidad y posición de los rayos X difractados, y su análisis posterior por medios matemáticos permite obtener una representación a escala atómica de los átomos y moléculas del material estudiado.
Max von Laue realizó los primeros experimentos de cristalografía de rayos X en 1912. Von Laue, William Henry Bragg y William Lawrence Bragg desarrollaron inicialmente la teoría de difracción de cristales, tarea a la que pronto se sumaron otros científicos. A lo largo del siglo XX tuvieron lugar varios avances teóricos y técnicos, como la aparición de los superordenadores y el uso de sincrotrones para la producción de rayos X, que incrementaron la capacidad del método para determinar las propiedades estructurales de todo tipo de moléculas: sales, materiales inorgánicos complejos, proteínas y hasta componentes celulares como los ribosomas. Es posible trabajar con monocristales o con polvo microcristalino, consiguiéndose diferentes datos en ambos casos: para las aplicaciones que requieren solo una caracterización precisa de los parámetros de la red cristalina, puede ser suficiente la difracción de rayos X por polvo; para una dilucidación precisa de las posiciones atómicas es preferible trabajar con monocristales.
Dada la relación existente entre la estructura tridimensional de las moléculas y sus propiedades químicas y físicas, la cristalografía ha contribuido al avance en varias disciplinas científicas como la química, la biología molecular, la geología, la física aplicada y la ciencia de materiales. La amplia disponibilidad de tubos de rayos X, complementada con el desarrollo de fuentes de rayos X de alta intensidad ha aumentado significativamente su impacto en estos campos de investigación así como en áreas con aplicaciones industriales, como el desarrollo de fármacos y la mineralogía aplicada. La mayor limitación de este método es la necesidad de trabajar con sistemas cristalinos, por lo que no es aplicable a disoluciones, a sistemas biológicos in vivo, a sistemas amorfos o a gases. En algunos casos, los rayos X pueden romper los enlaces químicos que mantienen la integridad estructural, lo que resulta en un modelo distorsionado de la molécula estudiada. Este problema afecta especialmente a los materiales de interés biológico.
Historia[editar]
Primeros experimentos[editar]
La idea de que los cristales son una repetición periódica de un grupo de moléculas ya existía anteriormente a que Wilhelm Conrad Röntgen descubriera los rayos X en 1895. Aunque las distancias típicas entre los planos de la red cristalina se desconocían, se sabía que debían ser muy pequeñas comparadas con la longitud de onda de la luz visible. Esto le dio al físico alemán Max von Laue la idea de utilizar cristales de sulfato de cobre para determinar si los rayos X se componían de partículas u ondas: dedujo que, si fueran ondas, deberían generar un patrón de difracción al atravesar los cristales.[n. 2] Los experimentos se realizaron en 1912, con la ayuda de Walter Friedrich y Paul Knipping, ambos antiguos estudiantes de Röntgen. Estos experimentos confirmaron la presencia de difracción cristalina, interpretada por von Laue como la extensión a tres dimensiones de la difracción de Fraunhofer por un enrejado.
Poco después, los británicos William Henry Bragg y William Lawrence Bragg (padre e hijo respectivamente) reprodujeron el experimento. W.L. Bragg explicó la difracción como la interferencia de los rayos X reflejados por planos cristalinos paralelos, introduciendo la descripción conocida desde entonces como la ley de Bragg.[1] En 1913, Paul Ewald demostró que las dos interpretaciones de los resultados publicadas independientemente por von Laue y Bragg eran equivalentes.[2] Von Laue recibió el premio Nobel de Física en 1914 por su descubrimiento del fenómeno, y los Bragg recibieron el mismo premio un año más tarde por su trabajo en las aplicaciones prácticas.[n. 3][3] Hacia el final de la década, se había logrado determinar las longitudes de onda de los rayos X y la estructura de varios compuestos inorgánicos simples y se habían establecido las bases teóricas de la técnica gracias al trabajo de los ya mencionados investigadores, Charles Galton Darwin[n. 4] y Peter Debye, entre otros.
El desarrollo de la técnica: 1920-1960[editar]
El período entre 1920 y 1960 se caracterizó por importantes adelantos metodológicos que propiciaron el empleo de la difracción de rayos X para analizar estructuras de moléculas más complejas.
Durante la década de 1920, los avances de la teoría cuántica sirvieron para caracterizar más precisamente la interacción entre los rayos X y los átomos de los cristales; esto posibilitó el análisis correcto de la intensidad de la difracción. En la misma época aparecieron las tablas para determinar la simetría cristalina a partir de la distribución de reflexiones en el patrón de difracción y se empezaron a usar las series de Fourier para representar la distribución de electrones en la red cristalina. Los desarrollos en la representación matemática de la densidad electrónica continuaron hasta la Segunda Guerra Mundial, facilitando la obtención de las primeras estructuras de moléculas orgánicas. En 1935, el cristalógrafo británico Arthur Patterson descubrió un truco matemático para obtener las distancias interatómicas directamente a partir de los datos experimentales, lo que supuso un importante avance en el análisis de la difracción.[4]
Entre las décadas de 1940 y 1960, surgieron otros procedimientos para la determinación de estructuras, especialmente, métodos heurísticos basados en el proceso de ensayo y error, que demostraron ser bastante exactos en combinación con restricciones condicionantes basadas en las propiedades físicas de una estructura correcta, como por ejemplo, que la densidad electrónica debe ser siempre positiva. En este período la cristalografía empezó a adquirir importancia en el campo de la química orgánica, proceso que culminó con la determinación en 1957 de la estructura de la vitamina B12, un proyecto liderado por Dorothy Hodgkin.[4]
Avances en cristalografía de macromoléculas: 1960-1980[editar]
El adelanto más trascendente durante las décadas de los 60 y 70 fue el reconocimiento de la cristalografía de proteínas y de moléculas involucradas en procesos biológicos en general como área de investigación clave en la biología molecular. El año 1962 marcó un hito al otorgarse dos premios Nobel por los resultados obtenidos usando métodos cristalográficos en esta área: el premio Nobel de Química fue concedido a Max Perutz y John Kendrew por sus estudios cristalográficos de las proteínas hemoglobina y mioglobina y el premio Nobel de Medicina a Francis Crick, James Watson y Maurice Wilkins por descubrir que el ADN forma una doble hélice.[n. 5] En 1964 Dorothy Hodgkin también obtuvo el premio Nobel de Química por la determinación de varias estructuras de importancia biológica, como la penicilina y la vitamina B12, entre otras.[6]
Un adelanto que facilitó en gran medida el éxito de las técnicas cristalográficas tanto en el caso de macromoléculas orgánicas con un gran número de átomos como en el de moléculas de menor tamaño fue el desarrollo de ordenadores digitales; gracias a ellos fue posible usar programas para medir y analizar fácilmente los datos obtenidos en los experimentos en vez de realizar los laboriosos cálculos manualmente.[7] Sin embargo, al final de este período el estudio de proteínas estaba aún limitado por la ausencia de fuentes de rayos X intensos y el empleo de película fotográfica para medir los patrones de difracción, lo que requería un largo proceso de revelado y digitalización de las imágenes.[n. 6] A consecuencia de estas limitaciones, y a pesar del reconocimiento generalizado del potencial de la cristalografía para estos experimentos, a finales de la década de 1970 el Banco de Datos de Proteínas solo contaba con unas sesenta entradas.[8]
Expansión y madurez: 1980-2010[editar]
Los tubo de rayos X, con sucesivas mejoras, se utilizaron como la fuente primordial de rayos X para los experimentos de cristalografía desde sus comienzos hasta la década de 1970, época en la que se empezó a experimentar con la radiación de sincrotrón de rayos X. Los sincrotrones dedicados exclusivamente a la producción de rayos X aparecieron en la década de 1980 y su número no ha dejado de aumentar desde entonces.[n. 7] En la primera década del siglo XXI se construyeron los primeros láseres de electrones libres de rayos-X, capaces de producir haces de luz pulsada de una intensidad de órdenes de magnitud mayor que en las fuentes de luz sincrotrón convencionales. La duración de los pulsos de luz, del orden de femtosegundos ofrece la posibilidad de observar cambios en los cristales a escalas temporales inalcanzables anteriormente.[7] Durante estos años también se desarrollaron nuevos detectores bidimensionales o «de área», capaces de generar directamente una imagen digitalizada del patrón de difracción. Estos detectores facilitaron la rápida medición y análisis de la difracción y sustituyeron totalmente a las placas fotográficas usadas hasta entonces.
Los mencionados avances, unidos al incremento de la capacidad de los ordenadores modernos para almacenar y procesar datos, han permitido llevar a cabo experimentos antaño irrealizables, y han desembocado en un aumento exponencial del número de estructuras elucidadas por métodos cristalográficos. El desarrollo más notable ha tenido lugar en el área de las macromoléculas orgánicas, con más de 88 000 estructuras depositadas en el Banco de Datos de Proteínas al comienzo de 2013.[8] La obtención en 2000 de la estructura del ribosoma,[9] un enorme complejo de ácidos nucleicos y varias proteínas donde tiene lugar la síntesis de proteínas en la célula, ilustra las capacidades que ha alcanzado la técnica.
Aspectos físicos[editar]
Cristales y redes cristalinas[editar]

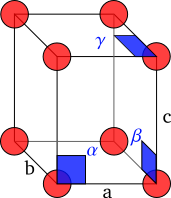
Los cristales están formados por una repetición periódica de moléculas en tres dimensiones. El cristal se puede representar matemáticamente como una red tridimensional, llamada «red de Bravais», en la que todas las intersecciones, o nodos, son idénticas.[10][11] El paralelepípedo definido por las líneas entre distintos nodos de la red se conoce como la celda unidad; aunque para una red dada sea posible designar múltiples celdas unidad que cumplan esta definición, por convención se escoge habitualmente la de menor volumen que refleje la simetría del cristal.[12][11] La celda unidad se define por la longitud de sus lados , y en la dirección de los tres ejes espaciales y los ángulos , y que los ejes de la red forman entre sí. Las coordenadas de cualquier punto de la red cristalina se pueden expresar como una combinación lineal de los vectores , y .[13]
La posición de un átomo en la celda unidad se expresa como coordenadas fraccionarias de , y de la siguiente forma:
con las coordenadas (, , ) comprendidas entre 0 y 1.[14]
El objetivo de los experimentos de difracción por rayos X es averiguar , y para cada átomo. Para lograrlo es necesario, en primer lugar, determinar la relación entre la red cristalina y la geometría del patrón de difracción y, en segundo lugar, obtener las posiciones de los átomos a partir de la intensidad de la difracción.
Rayos X[editar]

Los rayos X son un tipo de radiación electromagnética con longitudes de onda entre 10 y 10-2 nm o energías entre 0,1 y 100 keV.[15] Para los experimentos de difracción cristalina se suelen usar rayos X de energía relativamente alta, del orden de 10 keV, correspondiente a longitudes de onda del orden de 0,1 nm.[16][17]
Los rayos X se describen matemáticamente como una onda sinusoidal propagándose a través del espacio.
Tomando un punto arbitrario como origen, el valor del campo eléctrico en función del tiempo se puede escribir como:[18][19]
es la amplitud de la oscilación, la longitud de onda y la velocidad de la luz. A consecuencia de la interacción con los electrones de los átomos en la muestra, la onda sufre un desfase con respecto a la onda en el punto de origen:
La diferencia de fase depende de la distancia entre el punto de origen y los átomos del material; esto implica que la estructura atómica, es decir, las posiciones que ocupan los átomos, se pueden derivar de la fase de los rayos X que han atravesado el material.
Dispersión elástica de rayos X[editar]
El fenómeno de difracción cristalina tiene su origen en la dispersión elástica o scattering elástico del haz de rayos X por los átomos del cristal.[n. 8] En este tipo de interacción, el electrón desvía los rayos X, que toman exactamente la misma trayectoria que un rayo de luz visible reflejado en un espejo, es decir, los rayos dispersados emergen a un ángulo con respecto a la dirección de los rayos incidentes.[n. 9] Tanto el electrón como los rayos X conservan su energía inicial durante esta interacción.[20]
La dispersión elástica por un grupo de átomos en una dirección dada se puede cuantificar con una cantidad conocida como factor de estructura que es igual a la suma de los rayos reflejados por cada átomo que interactúa con los rayos incidentes[n. 10][21]
es una función llamada factor de forma atómica —o factor de dispersión atómica— que describe la dispersión por todos los electrones del átomo en conjunto. La dispersión elástica atómica depende del número atómico y del ángulo de incidencia de los rayos X.[22] El cambio de fase de los rayos dispersados durante la interacción viene dado por el producto escalar de , el vector entre el origen y cada átomo y , conocido como vector de dispersión, con magnitud y dirección perpendicular al plano virtual de reflexión.
Difracción cristalina[editar]
Ley de Bragg[editar]
La difracción en una dirección dada se debe esencialmente a la relación entre las fases de todas las ondas reflejadas por cada celda unidad del cristal en esa dirección. Los rayos que han atravesado distintos puntos del cristal siguen caminos ópticos de diferente longitud y esta diferencia da lugar a un cambio en la amplitud de la onda resultante; cuando la diferencia de fase es de 180 grados, las ondas se anulan entre sí. Por el contrario, cuando las ondas están en fase, la amplitud de la onda final es la suma de las amplitudes para cada onda. Puesto que un cristal está compuesto de un gran número celdas unidad, la interferencia constructiva entre todas ellas resulta en un haz lo suficientemente intenso para poder ser medido con un detector de rayos X.

La condición para que las ondas estén en fase es que la diferencia de sus caminos ópticos sea cero o un múltiplo entero de la longitud de onda. En un cristal, la diferencia en el camino óptico entre átomos situados en posiciones equivalentes en distintas celdas unidad es donde es la distancia entre los planos imaginarios que unen los puntos equivalentes de la red cristalina. Es decir, para que se observe interferencia constructiva de rayos X a un ángulo de observación , se debe cumplir la expresión conocida como Ley de Bragg:[23]
Como en el caso de la dispersión elástica por un átomo, la difracción cristalina se puede interpretar como la reflexión especular de los rayos X por todos los planos del cristal a un ángulo del haz incidente y separados entre sí por la distancia que cumple la ley de Bragg. Por este motivo, los puntos del patrón de difracción se denominan «reflexiones».[24]
Índices de Miller[editar]
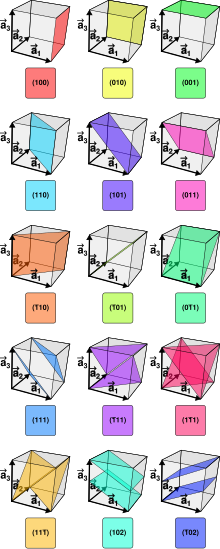
Para que se cumpla la ley de Bragg para un grupo de planos de reflexión paralelos, estos deben cruzar los ejes de la celda unidad un número entero de veces. Las reflexiones cristalinas se identifican mediante tres números , y iguales al número de intersecciones de los planos con los ejes , y de la celda. Los números , y reciben el nombre de índices de Miller. Matemáticamente, los índices de Miller describen un vector perpendicular al plano de reflexión en el sistema de coordenadas definido por la red cristalina.[25]
La red recíproca[editar]
Se denomina red recíproca a la transformada de Fourier de la red cristalina. Esta construcción matemática facilita la representación de los planos de reflexión y la visualización de la relación entre la orientación del cristal y el patrón de difracción. Las coordenadas de cada punto de la red recíproca coinciden con los índices de Miller, es decir, cada punto de la red recíproca representa a una familia de planos de Miller en el espacio real de la red cristalina; la distancia del origen a cada punto de la red es .[26][27]
Al igual que en el caso de la red cristalina, los puntos de la red recíproca se pueden expresar como una combinación lineal de vectores , y :[26]
La relación entre los parámetros de la celda unidad (, , , , , ) de volumen y la celda unidad recíproca (, , , ,, ) es la siguiente:[28][27]

La esfera de Ewald[editar]
Para visualizar fácilmente los planos de Miller que contribuyen a la difracción en una dirección dada y determinar la relación entre la orientación del cristal y el patrón de difracción, se utiliza la construcción conocida como esfera de Ewald. La esfera de Ewald ilustra todas las posibles direcciones en que los rayos X pueden ser reflejados por el cristal. El radio de esta esfera es y su extremo en la dirección del haz de rayos X incidente coincide con el origen de la red recíproca.[24][26]
Si un punto de la red recíproca de coordenadas se encuentra sobre la superficie de la esfera de Ewald, los planos de Miller con índices darán lugar a un punto de difracción en la dirección definida por el centro de la esfera y ese punto de la red recíproca. La distancia entre el origen y es , por lo que se puede demostrar geométricamente que esta condición de difracción es equivalente a la ley de Bragg.[26]
El factor de estructura cristalino[editar]
El vector con coordenadas en la red recíproca es perpendicular al plano de reflexión y su magnitud es ; es decir, es un vector de dispersión , introducido en la definición del factor de estructura , para el que se cumple la ley de Bragg. Por lo tanto, el factor de estructura en la dirección definida por los planos de Miller descritos por los índices se reformula como[29][n. 11]
donde es el vector de coordenadas del átomo en el sistema definido por la celda unidad y la suma se realiza para todos los átomos contenidos en ella. En lugar de sumar las contribuciones de cada átomo, también se puede realizar una integración sobre los electrones en el volumen de la celda unidad, cuya distribución por elemento de volumen se representa por la función de densidad electrónica :[30]

La aplicación de las operaciones de simetría del cristal a las coordenadas resulta en relaciones de igualdad entre los factores de estructura de diferentes reflexiones. A las reflexiones así relacionadas se las denomina «simétricamente equivalentes». En los experimentos cristalográficos, donde el grupo de simetría no se conoce con certeza a priori, se comparan las reflexiones relacionadas por diversas operaciones de simetría para caracterizar la simetría del cristal. La igualdad entre los módulos o «amplitudes» de las reflexiones relacionadas por un centro de inversión, con índices de Miller y
se conoce como ley de Friedel y ocurre incluso en la ausencia de simetría, aparte de la traslación de la celda unidad sobre la red cristalina.[31] En la práctica la ley de Friedel no se cumple exactamente debido a la presencia de interacciones inelásticas entre los rayos X y los átomos, que resultan en absorción de energía por estos.[32] Esos efectos suelen ser pequeños comparados con las interacciones elásticas y no se suelen tener en cuenta, excepto para longitudes de onda en la vecindad de una discontinuidad de absorción del cristal.
El problema de las fases[editar]
El propósito de los experimentos cristalográficos no es obtener el patrón de difracción, sino el valor de la función de distribución electrónica , lo que permite determinar la posición de los átomos y la estructura tridimiensional de la molécula cristalina. Se puede demostrar que puede representarse como sumas de Fourier de los factores de estructura en todas las direcciones:[33]
Mientras que el módulo del factor de estructura es simplemente la raíz cuadrada de la intensidad del punto de difracción, medida por un detector sensible a los rayos X, la fase no se puede computar directamente. Esto se conoce como el «problema de las fases».[34] Existen varios métodos para resolver el problema de las fases y elucidar la estructura atómica, clasificados en los siguientes grupos:[35]
- Métodos de Patterson
- Métodos directos
- Dispersión anómala
- Reemplazamiento isomorfo
- Reemplazamiento molecular
Método de Patterson[editar]
La función de Patterson se calcula efectuando la síntesis de Fourier con el cuadrado de los factores de estructura como coeficientes. Esta función se puede calcular directamente a partir de los datos experimentales, al no depender de la fase de los factores de estructura. En 1935, Arthur Patterson se percató de que los máximos de esta función corresponden a los vectores que se pueden trazar entre cada par de átomos en la celda unidad, lo cual se puede utilizar en ciertos casos favorables para determinar la posición de todos o algunos átomos. En particular, el análisis de la función de Patterson se utiliza a menudo para localizar los átomos causantes de diferencias isomorfas o anómalas, lo cual es a su vez el primer paso para solucionar el problema de las fases por estos otros métodos.[36][37][38]
Métodos directos[editar]
La función de distribución de densidad electrónica se caracteriza por ser siempre positiva y alcanzar valores máximos alrededor de los átomos. Estas y otras propiedades derivadas de principios básicos, expresadas en forma matemática, se utilizan para discriminar entre valores de las fases que resultan en una estructura con características físicamente posibles y los que no y, por eliminación de estos últimos, elucidar la estructura de la molécula de interés. Este método se usa corrientemente para resolver el problema de las fases para moléculas pequeñas.[39] En contraste, en el caso de los cristales de macromoléculas, los métodos directos no suelen ser suficientes para resolver la estructura totalmente ab initio sin ninguna información experimental adicional; esto se debe a que, por un lado, los cristales de proteínas y moléculas de similar tamaño raramente difractan a una resolución suficiente para obtener el número de reflexiones requerido para determinar todos los parámetros atómicos y, por otro lado, al gran número de átomos en la celda unidad, que causa que las relaciones entre las probabilidades de las fases sean menos determinantes que en los casos de moléculas que cuentan con pocos átomos.[40][41]
A pesar de los límites del método, sus principios también se aplican en el área de difracción de macromoléculas para mejorar las fases obtenidas por otros métodos y el cálculo de las fases a partir de un modelo de baja resolución. En la cristalografía de proteínas, las propiedades claves para discriminar entre fases correctas e incorrectas incluyen:[42]
- El contraste entre las zonas de la celda unidad ocupadas por moléculas de agua o solvente en estado amorfo y las zonas ordenadas ocupadas por la molécula.
- Una distribución característica de la probabilidad de valores de la densidad electrónica.
Al igual que la función de Patterson, los métodos directos también se utilizan para determinar las posiciones de átomos especiales en los métodos de sustitución o reemplazamiento isomorfo y de dispersión anómala.
Reemplazamiento isomorfo[editar]
El reemplazamiento isomorfo o sustitución isomorfa es un método para resolver el problema de las fases empleado predominantemente en cristalografía de macromoléculas. Consiste en la introducción en el medio de cristalización de un compuesto químico de pequeño tamaño conteniendo un átomo pesado, es decir de un número atómico elevado. Los compuestos de mercurio, platino, uranio, y oro son los más utilizados, entre muchos otros.[43][n. 12] Para que el método tenga éxito se debe establecer un enlace químico entre la molécula de interés y el átomo pesado, y la molécula modificada o «derivada» debe formar cristales isomorfos, con la misma simetría que los obtenidos a partir de la molécula «nativa» sin modificar. El factor de estructura de la molécula derivada es la suma del factor de estructura «nativo» y la contribución del átomo pesado .
Las fases del átomo pesado que contribuyen a esto se pueden calcular por métodos directos a partir de las diferencias . Aunque una sola sustitución isomorfa no es suficiente para determinar , si se repite el proceso con al menos una segunda estructura derivada diferente, es posible determinar las fases para la estructura nativa, por el método conocido como reemplazamiento isomorfo múltiple o sus siglas en inglés MIR (Multiple Isomorphous Replacement)[n. 13][44]
Las principal limitación de este método estriba en la dificultad de encontrar compuestos que reaccionen con la molécula a estudiar sin destruir al mismo tiempo el cristal o modificar sensiblemente su simetría o las dimensiones de la celda unidad.
Dispersión anómala[editar]

El factor de forma atómica no solo describe la dispersión elástica, sino también el efecto fotoeléctrico, que tiene lugar cuando los electrones cambian su estado cuántico al absorber parte de la energía de los rayos X. El término que corresponde a la dispersión inelástica o «anómala» es un número complejo .[45] Ambas componentes real e imaginaria alteran la magnitud de los factores de estructura. La componente imaginaria, relacionada con el coeficiente de absorción, introduce además un cambio de fase que resulta en diferentes magnitudes de los pares Friedel y , idénticas en ausencia de este efecto.
La contribución anómala al factor de estructura es menor que la contribución elástica y a menudo no es necesario tenerla en cuenta. Sin embargo, depende de la longitud de onda de los rayos X y experimenta grandes variaciones cuando la energía del haz incidente es similar a la energía de un nivel atómico del átomo. Cuando y alcanzan sus valores máximos los cambios en la magnitud y fase de los factores de estructura pueden ser significativos. Si algunos átomos en la molécula resultan afectados por este tipo de interacción, se pueden hallar sus posiciones en la celda unidad analizando las diferencias de intensidad entre las mismas reflexiones medidas a distintas longitudes de onda, o entre los pares de Friedel a la misma longitud de onda. Dichas diferencias se pueden utilizar para resolver el problema de las fases, por el método MAD (Multiwavelength Anomalous Dispersion/Diffraction o ‘dispersión/difracción anómala a múltiples longitudes de onda’)[46] o SAD (Single-wavelength Anomalous Dispersion/Diffraction o ‘dispersión/difracción anómala a una sola longitud de onda’)[n. 14]
La mayoría de los átomos pesados usados en el método de reemplazamiento isomorfo exhiben una dispersión anómala importante en el rango de longitudes de onda usado en los experimentos cristalográficos, por lo cual estas dos técnicas se usan a veces en conjunción. La ventaja de los métodos basados en la dispersión anómala es que, al precisar en principio solo un cristal para determinar las fases, no están limitados por un isomorfismo imperfecto. El uso de radiación sincrotrón, que se puede sintonizar a las longitudes de onda que optimizan la dispersión anómala, ha resultado en un fuerte incremento de la popularidad del método.
Reemplazamiento molecular[editar]
El método de reemplazamiento molecular consiste en el empleo de una molécula de estructura conocida para calcular las fases iniciales de una segunda molécula con elementos estructurales comunes con la primera. Este es el método más usado para determinar la estructura de macromoléculas como las proteínas, ya que muchas de ellas se agrupan en familias con una estructura similar o forman complejos supramoleculares en los que se conoce la estructura de una o más componentes.[48][49]
La desventaja del reemplazamiento molecular es que las fases obtenidas están sesgadas hacia la estructura utilizada como punto de partida, lo que no ocurre con las técnicas basadas enteramente en los datos de difracción experimentales y conocimiento a priori de las propiedades químicas o estructurales del material. El éxito de este método depende de algoritmos sofisticados para detectar y eliminar este sesgo durante el refinamiento de las fases.[49]
Refinamiento de la estructura[editar]
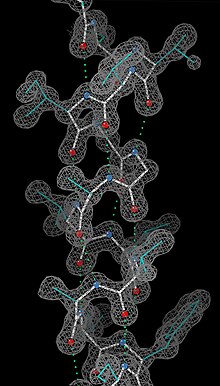
Una vez calculada la función a partir de las fases, se puede construir un modelo de la estructura en el mapa de densidad electrónica, descrito por un número de parámetros: las posiciones de cada átomo , y , su factor de temperatura representando los desplazamientos de los átomos con respecto a su posición media, etc.[50][n. 15] La determinación inicial de estos parámetros puede ser incorrecta, debido a errores en la determinación de las fases o fallos de interpretación de la densidad electrónica.[51] Durante el refinamiento, se modifica reiterativamente el modelo y a continuación se compara el módulo de los factores de estructura calculados a partir de este con el de los factores de estructura experimentales , hasta que la diferencia entre ambos sea mínima. La figura de mérito utilizada para la comparación es el factor R, definido como:[50]
La suma se realiza sobre todas las reflexiones .
Se usan dos técnicas matemáticas para ajustar los parámetros del modelo durante el refinamiento: los mínimos cuadrados y la máxima verosimilitud. El segundo método requiere más recursos computacionales, pero es más general y se aplica con preferencia en problemas difíciles, como macromoléculas y difracción a baja resolución.[52][53]
Cristalización[editar]

Para obtener datos de difracción de un cristal, este debe cumplir ciertos requisitos en cuanto a tamaño, pureza y regularidad de la red cristalina. Aunque a veces es posible utilizar cristales de metales o minerales inorgánicos formados por medios naturales, a menudo es necesario prepararlos mediante recristalización o precipitación del material en una solución líquida sobresaturada en condiciones controladas de concentración y temperatura. En el método de cristalización por difusión de vapor, la solución que contiene el material a cristalizar junto con un precipitante alcanza un estado de equilibrio termodinámico con otra solución más concentrada del precipitante, por difusión del disolvente hacia esta a través del aire; esta técnica se usa tanto para moléculas de pocos átomos como para proteínas y otras macromoléculas.[54][55] Un segundo método es la cristalización en geles, muy útil para cristalizar materiales insolubles; esta técnica, lenta comparada con la difusión de vapor,[54] consiste en la introducción de un reactante en un gel antes de que este se endurezca. Posteriormente se introduce otra solución de un segundo reactante en la capa superior del gel, desde donde se difunde al resto de la matriz y reacciona con la primera sustancia para dar lugar a cristales.[56]
Las condiciones de preparación de cristales deben también ser las adecuadas para obtener cristales de un tamaño óptimo para su estudio por difracción de rayos X; la talla ideal está determinada por la densidad y composición de la muestra: mientras que los cristales de gran tamaño atenúan excesivamente los rayos X y suelen presentar irregularidades en la matriz cristalina, los de talla muy pequeña difractan débilmente. En el caso de cristales de materiales orgánicos, son preferibles los cristales de unas décimas de milímetro; no obstante, cuando se usan fuentes de rayos X muy intensas, como láseres de electrones libres o líneas de luz sincrotrón modernas, es posible trabajar con cristales de dimensiones de unos veinte μm o incluso menores.[57][58] Para las aplicaciones de cristalografía en polvo, se requieren al menos varios cientos de miligramos de material machacado hasta formar cristales de aproximadamente diez μm o menores.[59]
Adquisición de datos[editar]
Fuentes de rayos X[editar]

Los experimentos de cristalografía de rayos X se pueden realizar, o bien con un tubo de rayos X o usando la radiación sincrotrón emitida por aceleradores de partículas. En los tubos de rayos X, se aplica un voltaje para acelerar un haz de electrones producidos por calentamiento de un filamento de wolframio —el cátodo. Los electrones acelerados colisionan contra un material metálico —el ánodo— y durante la consiguiente desaceleración emiten radiación de Bremsstrahlung de espectro continuo, es decir, compuesta de múltiples longitudes de onda. El ánodo absorbe parte de los rayos X emitidos por los electrones y emite a su vez rayos X de las longitudes de onda características del metal. Por ejemplo, un ánodo de cobre emite principalmente en la longitud de onda de 1,5405 Å. La radiación de Bremsstrahlung y otras líneas de emisión características menos intensas se filtran con un metal absorbente. En el ejemplo del ánodo de cobre, se utiliza níquel, que es bastante transparente a los rayos X de 1,5405 Å, pero absorbe eficazmente la radiación a longitudes de onda menores, obteniéndose un haz de rayos X bastante monocromático.[60] Los tubos de rayos X son relativamente baratos y los laboratorios de investigación los suelen utilizar para realizar experimentos in situ.
La radiación sincrotrón se obtiene cuando un haz de electrones[n. 16] acelerados hasta alcanzar una velocidad cercana a la de la luz es desviado de su trayectoria por medio de un campo magnético. El espectro de la radiación sincrotrón depende del tipo de dispositivo magnético usado para curvar la trayectoria de los electrones: los imanes dipolares y wigglers procucen radiación de espectro continuo muy amplio, mientras que los rayos X emitidos por los onduladores presentan máximos de amplitud a ciertas longitudes de onda. La longitud de onda deseada para el experimento se puede seleccionar mediante un monocromador. Las fuentes de radiación sincrotrón emiten rayos X mucho más intensos que los generados por los tubos y son necesarias para mejorar la calidad de la difracción cuando los cristales son muy pequeños o están compuestos de átomos ligeros, que interaccionan débilmente con los rayos X.
Durante los años 2010 empezaron a entrar en funcionamiento varios láseres de electrones libres diseñados para la producción de rayos X. Los pulsos de radiación emitida por estos dispositivos son del orden de femtosegundos —entre tres y cuatro órdenes de magnitud menores que los producidos las fuentes de radiación sincrotrón convencionales— y de alta intensidad. Estas propiedades permiten la investigación de procesos físicos o químicos que tienen lugar en escalas de tiempo muy rápidas y el estudio de cristales del tamaño de una micra mediante la nueva técnica de «cristalografía en serie a escala de femtosegundos», especialmente relevante para la cristalografía de proteínas de membrana.[61]
Detectores[editar]
Existen varios tipos de detectores usados en los experimentos de cristalografía. El detector bidimensional más usado durante mucho tiempo fue la película fotográfica, actualmente reemplazada por otros detectores más sensibles a los rayos X. Otro detector clásico es el contador proporcional unidimensional, normalmente un detector de centelleo, instalado en un difractómetro y controlado por ordenador. Este tipo de detector mide las reflexiones una a una y todavía se usa para la cristalografía de moléculas pequeñas, pero es poco eficaz en los experimentos con macromoléculas, donde el número de reflexiones ronda entre 10 000 y 100 000.[62]
A partir de los años 1990 empezaron a aparecer nuevos detectores, como las «placas de imagen» (image plates). Las placas de imagen están recubiertas de un material fosforescente, donde los electrones incrementan su energía al absorber los rayos X difractados y son atrapados en este nivel en centros de color. Los electrones liberan la energía al iluminarse la placa con luz láser, emitiendo luz con intensidad proporcional a la de la reflexión. Estos detectores son un orden de magnitud más sensibles que la película fotográfica y poseen un margen dinámico superior en varios órdenes de magnitud, lo que facilita la medición simultánea de las reflexiones más intensas y las más débiles. Otros detectores usados en la actualidad son detectores electrónicos, conocidos como detectores «de área», que procesan la señal inmediatamente tras la detección de los rayos X. Pueden ser cámaras de ionización o una placa fosforescente acoplada a una cámara CCD.[63] En los años 2000 se empezaron a utilizar fotodiodos alineados formando una placa, denominados PAD (Pixel Array Detectors). Estos detectores se caracterizan por un gran margen dinámico y un tiempo muerto entre imágenes muy bajo, del orden de milisegundos.[64]
Geometrías de difracción[editar]
Existen tres métodos tradicionales para medir la difracción de rayos X: el método de Laue, el método de rotación y el método de polvo. Una nueva técnica, la cristalografía en serie, se ha desarrollado en las primeras décadas del siglo XXI.
Método de Laue[editar]

Consiste en hacer incidir en un cristal un espectro continuo de rayos X, de tal manera que para cada longitud de onda se cumple la ley de Bragg para diferentes puntos de la red recíproca. Esto posibilita medir todas o casi todas la reflexiones sin cambiar la orientación del cristal. Existen dos variantes del método de Laue: transmisión y reflexión. En el método de Laue por transmisión, el cristal se emplaza entre la fuente de rayos X y el detector. En método de reflexión, el detector se encuentra entre la fuente y el cristal, para detectar los haces difractados hacia atrás.[65]
A pesar de ser el método utilizado en los primeros experimentos cristalográficos, el método de Laue se usaba muy poco para la determinación de estructuras debido principalmente a la baja intensidad de la radiación de espectro continua producida por los tubos de rayos X en comparación con la emisión característica monocromática. El creciente uso de la radiación sincrotrón ha fomentado el resurgimiento del método. La capacidad de medir todos los datos necesarios para la determinación de la estructura en un corto tiempo lo convierte en el método más apropiado para el estudio de reacciones químicas que tienen lugar en pocos segundos, como catálisis por enzimas y zeolitas y los efectos de perturbaciones causadas por campos eléctricos, cambios de presión y temperatura, etc. en diversos materiales.[66]
Métodos de rotación de cristal[editar]


Se hace incidir un haz de rayos X monocromáticos sobre un cristal, que rota a una velocidad constante alrededor de un eje perpendicular a los rayos X. La rotación del cristal causa que todos los puntos de la red recíproca atraviesen consecutivamente la esfera de Ewald, logrando así medir las reflexiones necesarias. Existen diferentes variantes de este método. En el método de Weissenberg se usa una cámara de forma cilíndrica rodeando al cristal tal que el eje de rotación del cristal coincide con el eje del cilindro. La cámara se traslada a medida que el cristal gira para que las reflexiones estén separadas. En el método de precesión, la cámara es plana, y rota alrededor de un eje paralelo al eje de rotación del cristal. En ambos métodos se usa una pantalla para medir solo una sección bidimensional de la red recíproca en cada imagen.[67][68] Estos métodos facilitan la determinación de la orientación del cristal y los índices de las reflexiones, pero son lentos e ineficientes. Los avances en computación de los años 90 posibilitaron un diseño más simple, en el que el detector se mantiene estacionario detrás del cristal, usándose programas para hallar automáticamente la orientación y los parámetros cristalinos consistentes con el patrón de difracción observado.[69]
Método de polvo cristalino[editar]

En el método de polvo cristalino o de Debye-Scherrer,[n. 17] el cristal a analizar es pulverizado de tal manera que forme un conjunto de microcristales en todas las posibles orientaciones de la red recíproca. Con esta geometría todas las reflexiones se pueden medir en un solo patrón de difracción, consistente en círculos, uno para cada reflexión. Aunque el método de rotación de cristal resulta en valores más exactos de la intensidad de las reflexiones, el método de polvo es a veces la única opción cuando el material a estudiar no forma monocristales de un tamaño suficiente para producir difracción detectable. Este método se usa mayoritariamente cuando no es necesario determinar la estructura; por ejemplo, en el análisis de minerales presentes en una muestra.[70]
Cristalografía en serie[editar]
La cristalografía en serie consiste en trasladar un medio o una placa que contiene cristales —generalmente de un tamaño de micras o menor— a través de un haz de rayos X, mientras que un detector registra datos continuamente para medir la difracción generada por los cristales a medida que atraviesan el haz. Un grupo de investigadores dirigidos por Janos Hajdu propusieron este método en el año 2000 como una manera de sacar partido de la corta duración de los pulsos de radiación generados por los láseres de electrones libres de rayos X para obtener datos de microcristales o partículas biológicas —por ejemplo, virus— antes de su destrucción por los procesos de ionización inducidos por los rayos X.[71] El concepto, popularizado como «diffract before destroy», 'difractar antes de destruir',[72] fue demostrado experimentalmente poco tiempo después de que el primer láser de electrones libres —LCLS, ubicado en el Laboratorio Nacional de Aceleradores SLAC— entrara en funcionamiento en 2009.[73]
La técnica, denominada «cristalografía en serie de femtosegundos», experimentó un fuerte desarrollo en poco tiempo, gracias a los avances realizados en la preparación e identificación de microcristales; en el desarrollo de instrumentación para medir la difracción a alta velocidad; y en la introducción de nuevos programas y algoritmos para analizar los datos obtenidos.[74] La nueva tecnología ha sido adoptada también en las líneas de rayos X de los sincrotrones (cristalografía en serie de sinchrotrón); los pulsos de luz de los sincrotrones que permiten la investigación de muchos procesos y reacciones importantes que tienen lugar en una escala temporal del milisegundos y estas instalaciones son más numerosas y accesibles que los láseres de electrones libres.[61][75]
Existen dos métodos principales de transportar los microcristales al punto de interacción con los rayos X: el primero se basa en producir un goteo o un chorro muy fino de cristales en suspensión en un medio líquido más o menos viscoso que interseca el haz de rayos X. El segundo método, inspirado más directamente en las técnicas de rotación de cristales, consiste en distribuir los cristales sobre la superficie de un material transparente a los rayos X conectada a un diffractómetro convencional u otro aparato motorizado para poder escanear el área ocupada por los cristales.[76]
Aplicaciones[editar]
La cristalografía tiene muchas aplicaciones en una gran variedad de disciplinas científicas, como la mineralogía, la química, la biología molecular, la farmacología,[77] la geología, la física aplicada y la ciencia de materiales.[78][79][80] Asimismo, las diferencias en el patrón de difracción de diversos materiales,[81][82] hielo,[83] sean minerales, drogas, pigmentos, adsorbentes,[84] catalizadores,[85][86][87] etc., con aspectos y composiciones químicas similares son de mucha utilidad en la industria y campos sin relación directa con la investigación científica básica o el desarrollo tecnológico, como la ciencia forense o la historia del arte.[88][89]
Premios Nobel[editar]

Varios de los descubrimientos y avances científicos que fueron llevados a cabo gracias a la cristalografía de rayos X han sidos galardonados con el Premio Nobel.[90] Entre ellos, una alta proporción se han otorgado a descubrimientos en química orgánica y biología; los primeros fueron los sendos premios en 1962 a Kendrew y Perutz en Química y Crick, Watson y Wilkins en Medicina, seguidos dos años más tarde por el galardón a Dorothy Hodgkin. Tras cuatro décadas de expansión, la cristalografía de macromoléculas empezó a contribuir de manera significativa al esclarecimiento de muchos procesos clave en la biología molecular y celular: En 1997, Boyer, Walker y Skou recibieron el Nobel de Química por elucidar el mecanismo de la síntesis del ATP; Roderick MacKinnon obtuvo dicho premio en 2003 por sus estudios de los canales de potasio en la membrana celular y Roger Kornberg en 2006 por el análisis de la maquinaria de transcripción genética. En 2009, fue otorgado a Ramakrishnan, Steitz y Yonath por el estudio de la estructura y función del ribosoma, complejo celular que lleva a cabo la síntesis de proteínas, y en 2012 a Lefkowitz y Kobilka por la investigación sobre los receptores acoplados a proteínas G, proteínas que permiten a las células detectar y responder a cambios en su entorno exterior.[6]
En el campo de la química inorgánica, la difracción con rayos X ha contribuido a la obtención de la estructura de los boranos, compuestos importantes para la síntesis química, por cuyo estudio la Academia recompensó a Herbert Brown con el Nobel de Química en 1979. Asimismo, la técnica se ha usado para determinar la estructura de los fulerenos, materiales con interesantes propiedades físicas y químicas. En 1996, Krotro, Smalley y Curl recibieron el premio por el descubrimiento de estas moléculas.[6]
En otras ocasiones se ha concedido premios Nobel por desarrollos teóricos y prácticos de la técnica misma, reconociendo su impacto científico; en esta categoría se incluyen los premios en Física a Max von Laue y William Henry y Lawrence Bragg, así como el de Química de 1936 a Peter Debye y el de 1985 para Hauptman y Karle por el desarrollo de los métodos directos para la solución de estructuras cristalinas.[6]
Análisis de minerales[editar]
La cristalografía de rayos X se utiliza no solo para obtener estructuras desconocidas, sino también para determinar la composición de muestras de suelos o minerales, así como para la identificación de metales y otros elementos. Cada sustancia mineral forma cristales con una celda unidad y simetría determinada, que resulta en un patrón de difracción característico. La difracción por el método de polvo es muy usada para este tipo de aplicaciones, por ser sencillo comparar el espaciado entre los anillos de difracción con los valores compilados por el Joint Committee on Powder Diffraction Standars (JCPDS).[70] Las proporciones relativas de dos o más minerales presentes en una misma muestra se obtienen comparando las intensidades de sus respectivas líneas con aquellas de muestras de composición conocida. Un ejemplo de esta aplicación es la identificación de minerales arcillosos, la fracción del suelo cuyas partículas minerales tienen un tamaño inferior a 2 μm.[91][92]
El vehículo explorador Curiosity, que aterrizó en Marte en 2012 para estudiar la superficie del planeta, cuenta entre sus instrumentos científicos con un difractómetro compacto equipado con un generador de rayos X y un detector de área.[93] En octubre de 2012, transmitió las primeras imágenes de difracción, que demostraron la presencia de minerales como feldespato, piroxeno y olivina en el suelo marciano, mezclados con material amorfo, a semejanza de los terrenos basálticos de los volcanes de Hawái.[94]
Diseño de fármacos[editar]
Desde finales de siglo XX se ha empezado a diseñar nuevos fármacos y medicamentos basados en inhibidores y sustratos naturales de diversas proteínas y enzimas involucradas en ciclos celulares y metabólicos. El conocimiento de la estructura de la parte de la proteína —la forma y la distribución de cargas electrostáticas— que liga estos compuestos facilita este proceso, gracias a la mejor comprensión de las interacciones entre la proteína y el ligando de interés; esto permite concentrarse en el diseño de fármacos con las características específicas deseadas.[95] Uno de los ejemplos más importantes de esta aplicación es el compuesto vemurafenib, diseñado para bloquear una enzima mutante presente en el 60 % de los casos de melanoma.[96]
Comparación con otras técnicas de difracción[editar]
Debido a la dualidad onda-partícula, es posible estudiar cristales mediante la difracción de un haz de neutrones o de electrones, además de con rayos X. Los primeros experimentos de difracción por electrones tuvieron lugar en 1926 y la difracción de neutrones se observó por vez primera en 1936. Aunque los experimentos y el análisis de datos obtenidos por cristalografía de electrones, neutrones y rayos X tienen mucho en común, existen algunas diferencias debidas a los diferentes modos de interacción con la materia: los electrones interaccionan tanto con el núcleo atómico como con los electrones que lo rodean y los factores de estructura cristalinos son unos cuatro órdenes de magnitud mayores que los resultantes de la dispersión elástica de rayos X, lo que posibilita el estudio de muestras de menor tamaño con electrones. Los neutrones, a su vez, son reflejados solo por el núcleo y no los electrones, aunque estos contribuyen indirectamente al factor de forma atómico mediante la creación de campos magnéticos; además, la interacción de la materia con ellos es mucho más débil que con los rayos X y es necesario usar reactores nucleares para generar haces de neutrones lo suficientemente intensos para obtener difracción cristalina.[97]
Una ventaja importante del uso de electrones es que las fases pueden obtenerse a partir de la transformada Fourier de las imágenes del objeto en un microscopio electrónico. En 1968, David DeRosier y Aaron Klug publicaron un método para reconstruir mapas de densidad electrónica tridimensionales basados en este principio.[98] Hasta la segunda década del siglo XXI, la mejor resolución espacial de estos mapas —alrededor de 0,4 nm— era baja comparada con los valores alcanzables con rayos X o neutrones, aunque la criomicroscopía electrónica era útil en casos donde no era posible cristalizar la molécula a estudiar o la estructura no podía determinarse por otros métodos, principalmente en el ámbito de la biología macromolecular.[99] El desarrollo de detectores directos de electrones y de técnicas computacionales para el procesamiento de imágenes han acercado la resolución de los mapas a la obtenida por cristalografía de rayos X.[100] Las desventajas de la criomicroscopía electrónica residen en las dificultades de preparación de las muestras y el elevado coste del equipo necesario para obtener datos de alta calidad.[101]
En lo que respecta a la cristalografía de neutrones, la ventaja principal estriba en la clara visualización de los átomos de hidrógeno, muy difíciles de detectar con rayos X debido a que solo poseen un electrón; esta propiedad constituye una ventaja para el estudio de aquellas moléculas orgánicas en cuya función tenga un papel importante el intercambio de hidrógeno.[102] Además, los neutrones no ionizan los átomos, por lo que no destruyen los enlaces moleculares durante el experimento.
Limitaciones[editar]
La limitación fundamental de la cristalografía de rayos X consiste en que solo puede aplicarse a sustancias susceptibles de formar cristales. Aunque las técnicas cristalográficas pueden utilizarse también para determinar la estructura de otros materiales con periodicidad espacial, como fibras helicoidales —ADN, algunos tipos de virus, etc.— y cuasicristales, resulta imposible estudiar gases, líquidos y sólidos desordenados por este método. Además, la obtención de cristales no es siempre suficiente para obtener la estructura de interés: las moléculas de tamaño grande, por ejemplo, suelen ser casos difíciles.[103]

Otro límite de la técnica está relacionado con el tipo de información que proporciona sobre la estructura: Los modelos obtenidos por difracción representan una media de las posiciones atómicas para todas las moléculas del cristal; cuando la molécula cuenta con átomos que oscilan entre diferentes conformaciones, la densidad electrónica media se extiende sobre la totalidad del espacio que pueden ocupar estos átomos y las partes desordenadas de la molécula resultan invisibles. Esto representa un serio problema para el estudio de enzimas si el sitio activo de la molécula —asociada a su actividad química— presenta una gran movilidad; en este caso la determinación de las propiedades de materiales biológicos in vivo a partir de su estructura cristalina es problemática y requiere métodos de estudio alternativos, como la resonancia magnética nuclear.
Las vibraciones atómicas también limitan la resolución alcanzable con los datos de difracción, incluso cuando las moléculas adoptan la misma conformación en distintas celdas unidad. La resolución del modelo no suele ser suficiente para determinar el estado de oxidación, posicionar todos los átomos de hidrógeno o distinguir elementos con números atómicos semejantes.[103][104] La débil interacción de los rayos X con los átomos ligeros es otra desventaja de la técnica en aplicaciones, como la caracterización de nanomateriales.[105]
Finalmente, las propiedades ionizantes de los rayos X pueden alterar o destruir las moléculas del cristal durante el experimento. Cuando esto ocurre, el modelo obtenido no refleja la verdadera estructura molecular y puede dar lugar a interpretaciones erróneas sobre sus propiedades. Además, las distorsiones globales de la red cristalina y otros efectos secundarios de la irradiación dificultan la obtención de las fases. Este problema es grave en cristales de proteínas, que contienen una alta proporción de agua y compuestos orgánicos fácilmente radiolizables, y un gran número de enlaces químicos susceptibles al ataque por los radicales libres y electrones producidos por dicha radiolisis. Los experimentos con moléculas biológicas se suelen realizar a temperaturas de 100 K o menores; esto frena la difusión de los radicales libres, aunque no soluciona enteramente el problema, pues los fotoelectrones excitados por los rayos X permanecen móviles hasta el cero absoluto.[106][107] Los cortos pulsos (alrededor de 10 fs) de los láseres de electrones libres de rayos X permiten obtener patrones de difracción por cristalografía en serie antes de que los procesos de ionización alteren la estructura de las moléculas. La técnica de cristalografía en serie también puede aplicarse en las líneas de luz de los sincrotrones más modernos; mientras que en un sincrotrón los pulsos de radiación son demasiado largos para impedir los efectos de la irradiación, estos son menores que en experimentos convencionales y el coste del experimento es menor que en un láser de electrones libres.[61]
Véase también[editar]
- Cristalografía
- Difracción de electrones
- Difracción de neutrones
- Espectroscopia de rayos X
- Resonancia magnética nuclear
Notas[editar]
- ↑ El término 'difracción de rayos X' se utiliza a menudo para referirse a la aplicación de este fenómeno a la cristalografía; sin embargo, es posible observar difracción por materiales no cristalinos. Por ejemplo, la estructura de la doble hélice de ADN se elucidó por primera vez usando datos de difracción de rayos X por fibras deshidratadas de ADN.
- ↑ Esta cuestión fue resuelta definitivamente cuando de Broglie introdujo en 1924 el concepto de la dualidad onda partícula.
- ↑ Debido al comienzo de la Primera Guerra Mundial, en la que Suecia deseaba mantenerse estrictamente neutral y no dar la impresión de que se favorecía a ningún país contendiente, los premios no fueron otorgados hasta después de la guerra.
- ↑ Nieto de Charles Darwin, autor de El origen de las especies.
- ↑ Rosalind Franklin, que realizó el análisis de los datos de difracción cruciales para determinar la estructura de la doble hélice, falleció antes de que se concediera el premio.[5]
- ↑ La medición individual de reflexiones de rayos X emergentes en diferentes direcciones con un fotodetector unidimensional, que facilitó la automatización de los experimentos con moléculas pequeñas durante este periodo no resultaba práctica en el caso de moléculas con muchos átomos, debido a la enorme cantidad de reflexiones presentes en este caso.
- ↑ Véase la lista en Anexo:Fuentes de luz sincrotrón.
- ↑ Desde el punto de vista de la electrodinámica cuántica, la dispersión elástica es simplemente un caso especial del efecto Compton.
- ↑ es el ángulo de incidencia respecto al plano de reflexión.
- ↑ El factor de estructura es una función compleja, representada habitualmente como un vector en el plano de Argand. Por este motivo, varios autores usan la nomenclatura vectorial utilizada aquí.
- ↑ La nomenclatura usada para designar al factor de forma cristalino varía; a menudo aparece como . Otras denominaciones comunes son , y . Las dos últimas son más utilizadas para describir la difracción en general que en el caso específico de la difracción cristalina.
- ↑ El factor de forma atómico f es proporcional al número atómico, por lo que la contribución al factor de estructura de un átomo pesado es significantemente mayor que la de los átomos ligeros (carbono, oxígeno, nitrógeno e hidrógeno) predominantes en las macromoléculas orgánicas.
- ↑ En ocasiones, si hay errores en los datos debidos a un isomorfismo imperfecto entre los cristales u otros factores, es necesario usar más de dos derivados para obtener fases lo suficientemente exactas.
- ↑ Se necesitan al menos dos longitudes de onda diferentes para resolver el problema de las fases solamente por este método, pero una longitud de onda basta si se aplican restricciones adicionales sobre la función de densidad electrónica.[47]
- ↑ El número de parámetros usados para representar el modelo depende de la resolución de la difracción. Para que el refinamiento sea efectivo, el número de reflexiones independientes —no relacionadas por simetría— debe ser mayor que los parámetros que se pretenden refinar.
- ↑ Es posible usar positrones u otra partícula con carga eléctrica para este fin, pero se usan electrones en la mayoría de los casos.
- ↑ Este método fue propuesto por Peter Debye y Paul Scherrer en 1916 e independientemente por Albert Hull en 1917.[4]
Referencias[editar]
- ↑ Bragg, William Lawrence Bragg (1913). Proc. Cambridge Philos. Soc. (en inglés) 17: 43-57.
- ↑ Ewald, Paul Peter (1913). Phys. Z. 14: 465-472.
- ↑ Eckert, Michael (2012). «Disputed discovery: the beginnings of X-ray diffraction in crystals in 1912 and its repercussions». Acta Crystallographica A (en inglés) 68: 30-30. doi:10.1107/S0108767311039985.
- ↑ a b c Bragg, William Lawrence; Ewald, Paul Peter (ed.) (1962). «The growing power of X-ray analysis» (PDF). Fifty Years of X-Ray Diffraction (en inglés). International Union of Crystallography. pp. 120-135.
- ↑ Osman Elkin, Lynne (2003). «Rosalind Franklin and the Double Helix». Physics Today (en inglés) 56 (3): 42. doi:10.1063/1.1570771.
- ↑ a b c d «All Nobel Prizes by Year» (en inglés). The official web site for the Nobel Prize. Consultado el 17 de enero de 2012.
- ↑ a b Schwarzenbach, Dieter (2012). «The success story of crystallography». Acta Crystallographica A (en inglés) 68: 57-67. doi:10.1107/S0108767311030303.
- ↑ a b «Yearly growth of structures solved by X-ray» (en inglés). RCSB Protein Data Bank. Archivado desde el original el 9 de octubre de 2016. Consultado el 6 de octubre de 2016.
- ↑ Ramakrishnan, Venki; Moore, Peter B. (2001). «Atomic structures at last: the ribosome in 2000» (PDF). Current Opinion in Structural Biology 11: 144-154. Archivado desde el original el 1 de febrero de 2013. Consultado el 20 de enero de 2012.
- ↑ Universidad de Cambridge. «Lattices» (en inglés). Consultado el 22 de marzo de 2012.
- ↑ a b Stout y Jensen, 1989, pp. 18-19.
- ↑ Universidad de Cambridge. «Unit cell» (en inglés). Consultado el 22 de marzo de 2012.
- ↑ Universidad de Cambridge. «Lattice geometry» (en inglés). Consultado el 22 de marzo de 2012.
- ↑ Drenth, 1999, p. 62.
- ↑ Stout y Jensen, 1989, p. 7.
- ↑ Stout y Jensen, 1989, p. 11.
- ↑ Helliwell, 1992, pp. 268-274.
- ↑ Drenth, 1999, pp. 71-74.
- ↑ Read,Randy (2009). «Advanced diffraction: waves, interference and complex numbers». Protein Crystallography Course (en inglés). Universidad de Cambridge. Consultado el 26 de marzo de 2012.
- ↑ Drenth, 1999, p. 75.
- ↑ Drenth, 1999, p. 88.
- ↑ Ozols,Andrés (2009). «Aplicaciones de la difracción de rayos X» (PDF). Facultad de Ingeniería, Universidad de Buenos Aires. Archivado desde el original el 6 de marzo de 2010. Consultado el 26 de marzo de 2012.
- ↑ IUCr (3 de febrero de 2012). «Bragg's law». Online dictionary of crystallography (en inglés). Consultado el 29 de marzo de 2012.
- ↑ a b «Ecuaciones de Laue. Ley de Bragg». Curso de cristalografía estructural. Universidad Nacional de Educación a Distancia, Facultad de Ciencias. Archivado desde el original el 29 de octubre de 2015. Consultado el 29 de marzo de 2012.
- ↑ IUCr (6 de febrero de 2012). «Miller indices». Online dictionary of crystallography (en inglés). Consultado el 3 de abril de 2012.
- ↑ a b c d IUCr (25 de mayo de 2007). «Reciprocal lattice». Online dictionary of crystallography (en inglés). Consultado el 29 de marzo de 2012.
- ↑ a b Stout, Jensen, pp. 26-33.
- ↑ Authier, André. «Reciprocal lattice» (pdf). Teaching pamphlets (en inglés). University College Cardiff Press, Cardiff, Wales; Versión digital: Unión Internacional de Cristalografía. ISBN 0 906449 08 1. Consultado el 11 de febrero de 2012.
- ↑ IUCr (1 de septiembre de 2011). «Structure factor». Online dictionary of crystallography (en inglés). Consultado el 9 de abril de 2012.
- ↑ Stout y jensen, 1989, p. 205.
- ↑ Stout y Jensen, 1989, p. 203.
- ↑ Unión Internacional de Cristalografía. «Friedel's law». Online Dictionary of Crystallography (en inglés). Consultado el 12 de marzo de 2012.
- ↑ Stout, Jensen, p. 209.
- ↑ Elies Molins y Joan F. Piniella (1995). «Determinación y aplicación de las densidades electrónicas precisas». En Félix Hernández Cano, Concepción Foces-Foces, Martín Martínez-Ripoll, ed. Cristalografía. Colección:Nuevas Tendencias 26. CSIC. pp. 61-62. ISBN 8400075579.
- ↑ Read, Randy (26 de febrero de 2012). «The phase problem: introduction to phasing methods». Protein Crystallography Course (en inglés). Cambridge University. Consultado el 12 de abril de 2012.
- ↑ Sout y Jensen, 1989, pp. 279-291.
- ↑ Luger, 1980, pp. 216-217.
- ↑ Unión Internacional de Cristalografía. «Patterson methods». Online Dictionary of Crystallography (en inglés). Consultado el 3 de abril de 2012.
- ↑ Stout y Jensen, 1989, p. 248.
- ↑ Karle, Jerome (1989). «Direct methods in protein crystallography». Acta Crystallographica A (en inglés) 45: 765-781. doi:10.1107/S0108767389007403.
- ↑ Sheldrick, George. M. (1998). S. Fortier, ed. Direct Methods for Solving Macromolecular Structures. Kluwer Academic Publishers. pp. 401-411.
- ↑ Jerónimo Bravo, Nuria Verdaguer e Ignacio Fita (1995). Modificación de la densidad electrónica en el afinamiento y extensión de las fases en macromoléculas. En Félix Hernández Cano, Concepción Foces-Foces, Martín Martínez-Ripoll, ed. «Cristalografía». Colección:Nuevas Tendencias 26 (CSIC). pp. 199-. ISBN 8400075579.
- ↑ Islam, Suhail A.; Carvin, David; Sternberg, Michael J. E.; Blundell, Tom L. (1998). «HAD, a Data Bank of Heavy-Atom Binding Sites in Protein Crystals: a Resource for Use in Multiple Isomorphous Replacement and Anomalous Scattering». Acta Crystallographica D (en inglés) 54: 1199-1206. doi:10.1107/S090744499800715X.
- ↑ Rupp, Bernhard (26 de diciembre de 2009). «Multiple Isomorphous Replacement (MIR) Phasing» (en inglés). Consultado el 27 de febrero de 2012.
- ↑ IUCr (3 de febrero de 2012). «Anomalous dispersion». Online dictionary of crystallography (en inglés). Consultado el 12 de abril de 2012.
- ↑ IUCr (11 de abril de 2008). «Multiwavelength anomalous diffraction (MAD)». Online dictionary of crystallography (en inglés). Consultado el 12 de abril de 2012.
- ↑ Dauter, Zbigniew; Dauter, Miroslawa; Dodson, Eleanor (2002). «Jolly SAD». Acta Crystallographica Section D 58: 494-506. doi:10.1107/S090744490200118X.
- ↑ Santiago García-Granda y Javier Borge (1995). Resolución estructural «Ab Initio» de moléculas orgánicas y proteínas por aplicación de funciones de rotación y traslación. En Félix Hernández Cano, Concepción Foces-Foces, Martín Martínez-Ripoll, ed. «Cristalografía». Colección:Nuevas Tendencias 26 (CSIC). pp. 199-. ISBN 8400075579.
- ↑ a b Dodson, Eleanor (2008). «The befores and afters of molecular replacement». Acta Crystallographica D 64: 17-24. doi:10.1107/S0907444907049736.
- ↑ a b Luger, 1980, p. 267.
- ↑ Read,Randy (2008). «Overview of macromolecular X-ray crystallography». Protein crystallography course. University of Cambridge. Consultado el 6 de abril de 2012.
- ↑ Drenth, 1999, p. 268.
- ↑ Read,Randy (2009). «Likelihood: theory and application to structure refinement». Protein crystallography course. University of Cambridge. Consultado el 6 de abril de 2012.
- ↑ a b Spingler, Bernhard; Schnidrig, Stephan; Todorova, Tonya; Wilda, Ferdinand (2012). «Some thoughts about the single crystal growth of small molecules». CrystEngComm (en inglés) 14: 751-757. doi:10.1039/C1CE05624G.
- ↑ Al Karadaghi, Salam (2012). «Protein Crystallization: Basic Approach». Experimental Methods in Structural Biology (en inglés). Archivado desde el original el 4 de diciembre de 2020. Consultado el 1 de octubre de 2013.
- ↑ Suib, Steven L. (1985). «Crystal growth in gels». J. Chem. Educ. (en inglés) 62 (1): 81-82. doi:10.1021/ed062p81.
- ↑ Smith, J.L.; Fischetti, R.F.; Yamamoto, M. (2012). «Micro-crystallography comes of age». Curr Opin Struct Biol. (en inglés) 22 (5): 602-612. doi:10.1016/j.sbi.2012.09.001.
- ↑ Chapman, H.N. et al (2011). «Femtosecond X-ray protein nanocrystallography». Nature (en inglés) 470: 73-77. doi:10.1038/nature09750.
- ↑ Dutrow, Barbara L. y Clark, Christine M. (24 de agosto de 2013). «X-ray Powder Diffraction (XRD)». Geochemical Instrumentation and Analysis (en inglés). Science Education Research Center at Carleton College. Consultado el 1 de octubre de 2013.
- ↑ Luger, 1980.
- ↑ a b c Helliwell, John R. (31 de agosto de 2017). «New developments in crystallography: exploring its technology, methods and scope in the molecular biosciences». Bioscience Reports (en inglés) 37 (4): BSR20170204. ISSN 0144-8463. PMC 6434086. PMID 28572170. doi:10.1042/BSR20170204. Consultado el 13 de diciembre de 2021.
- ↑ Drenth, 1999, p. 35.
- ↑ Drenth, 1999, pp. 34-35.
- ↑ Gruner, E F; Barna, S L; Tate, M W; Rossi, G; WixtedP J Sellin, R L (1998). «A Pixel-Array Detector for Time-Resolved X-ray Diffraction». Journal of Synchrotron Radiation (en inglés) 5: 252-255. PMID 15263487.
- ↑ «The Laue method». Matter, Universidad de Liverpool. 25 de julio de 2000. Archivado desde el original el 31 de mayo de 2012. Consultado el 27 de marzo de 2012.
- ↑ Helliwell, 1992, p. 276.
- ↑ Luger, 1980, pp. 52-79.
- ↑ Stout y Jensen, 1989, pp. 93-136.
- ↑ Jeffrey, Phil (febrero de 2006). «X-ray Data Collection Course» (en inglés). Archivado desde el original el 7 de enero de 2012. Consultado el 28 de marzo de 2012.
- ↑ a b «Métodos de difracción de rayos X». Curso de cristalografía. Universidad Nacional de Educación a Distancia, Facultad de Ciencias. Archivado desde el original el 29 de octubre de 2015. Consultado el 1 de abril de 2012.
- ↑ Neutze, Richard; Wouts, Remco; van der Spoel, David; Weckert, Edgar; Hajdu, Janos (2000-08). «Potential for biomolecular imaging with femtosecond X-ray pulses». Nature (en inglés) 406 (6797): 752-757. ISSN 0028-0836. doi:10.1038/35021099. Consultado el 17 de diciembre de 2021.
- ↑ Doerr, Allison (2011-04). «Diffraction before destruction». Nature Methods (en inglés) 8 (4): 283-283. ISSN 1548-7091. doi:10.1038/nmeth0411-283. Consultado el 17 de diciembre de 2021.
- ↑ Chapman, Henry N.; Fromme, Petra; Barty, Anton; White, Thomas A.; Kirian, Richard A.; Aquila, Andrew; Hunter, Mark S.; Schulz, Joachim et al. (2011-02). «Femtosecond X-ray protein nanocrystallography». Nature (en inglés) 470 (7332): 73-77. ISSN 0028-0836. PMC 3429598. PMID 21293373. doi:10.1038/nature09750. Consultado el 17 de diciembre de 2021.
- ↑ Schlichting, Ilme (1 de marzo de 2015). «Serial femtosecond crystallography: the first five years». IUCrJ (en inglés) 2 (2): 246-255. ISSN 2052-2525. PMC 4392417. PMID 25866661. doi:10.1107/S205225251402702X. Consultado el 17 de diciembre de 2021.
- ↑ Pearson, Arwen R; Mehrabi, Pedram (2020-12). «Serial synchrotron crystallography for time-resolved structural biology». Current Opinion in Structural Biology (en inglés) 65: 168-174. doi:10.1016/j.sbi.2020.06.019. Consultado el 21 de diciembre de 2021.
- ↑ Martiel, Isabelle; Müller-Werkmeister, Henrike M.; Cohen, Aina E. (1 de febrero de 2019). «Strategies for sample delivery for femtosecond crystallography». Acta Crystallographica Section D Structural Biology (en inglés) 75 (2): 160-177. ISSN 2059-7983. PMC 6400256. PMID 30821705. doi:10.1107/S2059798318017953. Consultado el 21 de diciembre de 2021.
- ↑ Fernandes, Julyane B.M.; Celestino, Maísa T.; Tavares, Maria I.B.; Freitas, Zaida M.F.; Santos, Elisabete P. Dos; Ricci Júnior, Eduardo; Monteiro, Mariana S.S.B. (8 de abril de 2019). «The development and characterization of Propranolol Tablets using Tapioca starch as excipient». Anais da Academia Brasileira de Ciências 91 (1). ISSN 1678-2690. doi:10.1590/0001-3765201920180094. Consultado el 2 de junio de 2019.
- ↑ Larsson, Letícia; Tractza, Gideã; Maia, Guilherme; Alves, Guilherme; Rodrigues, Paulo; Cunha, Maico; Banczek, Everson (2019). «COMPARATIVE STUDY OF TiO2 AND ZnO APPLICATION IN HYBRID SOLAR CELLS USING COPOLYMER P3OT/P3MT». Química Nova. doi:10.21577/0100-4042.20170344. Consultado el 2 de junio de 2019.
- ↑ T. Hahn, ed. (1990-1991). «Crystallography: current and future tasks» (en inglés). Deutsche Gesellschaft für Kristallographie. Archivado desde el original el 17 de mayo de 2014. Consultado el 13 de abril de 2012.
- ↑ Ibáñez Muñoz, Sonia. «¿Qué es la cristalografía de proteínas?». Archivado desde el original el 10 de junio de 2013. Consultado el 13 de abril de 2012.
- ↑ Iwamoto, Gerson Yoshinobu; Rodrigues, Christiane de Arruda; Iwamoto, Luciana Aparecida de Sousa; Vieira, Rogerio de Almeida (8 de abril de 2019). «New Peritectoid Reaction Identified at the MnSb Alloy». Materials Research 22 (suppl 1). ISSN 1980-5373. doi:10.1590/1980-5373-mr-2018-0647. Consultado el 2 de junio de 2019.
- ↑ Fontes, Marcos Alves; Scheid, Vladimir Henrique Baggio; Machado, David de Souza; Casteletti, Luiz Carlos; Nascente, Pedro Augusto de Paula (4 de abril de 2019). «Morphology of the DIN 100Cr6 Case Hardened Steel after Plasma Nitrocarburizing Process». Materials Research 22 (3). ISSN 1980-5373. doi:10.1590/1980-5373-mr-2018-0612. Consultado el 2 de junio de 2019.
- ↑ Angelos Michaelides; Slater, Ben (2019-03). «Surface premelting of water ice». Nature Reviews Chemistry (en inglés) 3 (3): 172-188. ISSN 2397-3358. doi:10.1038/s41570-019-0080-8. Consultado el 2 de junio de 2019.
- ↑ Schröder, Martin; Yang, Sihai; Han, Xue (2019-02). «Porous metal–organic frameworks as emerging sorbents for clean air». Nature Reviews Chemistry (en inglés) 3 (2): 108-118. ISSN 2397-3358. doi:10.1038/s41570-019-0073-7. Consultado el 2 de junio de 2019.
- ↑ «The reaction network in propane oxidation over phase-pure MoVTeNb M1 oxide catalysts». J. Catal. (311): 369-385. 2014.
- ↑ «Surface chemistry of phase-pure M1 MoVTeNb oxide during operation in selective oxidation of propane to acrylic acid». J. Catal. (285): 48-60. 2012.
- ↑ Kinetic studies of propane oxidation on Mo and V based mixed oxide catalysts (en inglés). 2011.
- ↑ Gabinete de comunicación de la Universidad Internacional Menéndez Pelayo (11 de agosto de 2011). «Expertos en Cristalografía lamentan la carencia de técnicos en España y apuestan por la divulgación para “fomentar las vocaciones”». Archivado desde el original el 19 de febrero de 2012. Consultado el 13 de abril de 2012.
- ↑ Fischer, R; Hellmiss, G (1989). «Principles and forensic applications of X-ray diffraction and X-ray fluorescence». En H. C. Lee y R. E. Gaensslen, ed. Advances in Forensic Sciences (en inglés) 2. Chicago: Year Book Medical Publishers, Inc. pp. 129-158. ISBN 081515349X.
- ↑ IUcr. «Nobel Prize winners associated with crystallography». Consultado el 13 de abril de 2012.
- ↑ Thorez, J. (1975). Phyllosilicates and Clay Minerals. A Laboratory Handbook for Their X-Ray Diffraction Analysis (en inglés). Lelotte.
- ↑ Iván Darío Gómez Guzmán, ed. (2006). Métodos Analíticos del Laboratorio de Suelos. Mineralogía de la Fracción Arcilla (6 edición). Colombia: IGAC (Instituto Geográfico Agustín Codazzi). ISBN 9789589067987.
- ↑ Matesanz, Emilio (30 de mayo de 2010). «Curiosity:DRXP en Marte». DRXP en la práctica. Archivado desde el original el 19 de diciembre de 2013. Consultado el 14 de octubre de 2013.
- ↑ Brown, Dwayne (30 de octubre de 2012). «NASA Rover's First Soil Studies Help Fingerprint Martian Minerals» (en inglés). NASA. Archivado desde el original el 3 de junio de 2016. Consultado el 14 de octubre de 2013.
- ↑ Greer, Jonathan; Erickson,, John W.; Baldwin, John J.; Varney, Michael D. (1994). «Application of the Three-Dimensional Structures of Protein Target Molecules in Structure-Based Drug Design». Journal of Medicinal Chemistry (en inglés) 37 (8): 1035-1054. doi:10.1021/jm00034a001.
- ↑ Hughes, Terry V.; Baldwin, Ian; Churcher, Ian (2011). «Fragment-based Drug Discovery - From Hit Discovery to FDA Approval: Lessons Learned and Future Challenges». International Drug Discovery (en inglés). Archivado desde el original el 9 de mayo de 2014.
- ↑ Ewald, Paul P. (1999) [1962]. «15.7: Electron and Neutron Diffraction» (PDF). En P.P. Ewald, ed. Fifty Years of X-Ray Diffraction (PDF edición). Unión Internacional de Cristalografía. pp. 261-264.
- ↑ DeRosier, D. J.; Klug, A. (1968). «Reconstruction of three dimensional structures from electron micrographs». Nature (en inglés) 217: 130-134.
- ↑ Zhu, Xiaodong Zou; Hovmöller, Sven; Oleynikov, Peter (2011). Electron Crystallography: Electron Microscopy and Electron Diffraction. International Union of Crystallography Texts on Crystallography (en inglés) 16. Oxford University Press. p. 4. ISBN 0199580200.
- ↑ Bai, Xiao-chen; McMullan, Greg; Scheres, Sjors H.W (2015-01). «How cryo-EM is revolutionizing structural biology». Trends in Biochemical Sciences (en inglés) 40 (1): 49-57. doi:10.1016/j.tibs.2014.10.005. Consultado el 15 de diciembre de 2021.
- ↑ «Focus on: Cryo-electron microscopy». RSB (en inglés). Archivado desde el original el 15 de diciembre de 2021. Consultado el 15 de diciembre de 2021.
- ↑ Blakeley, Matthew P; Langan, Paul; Niimura, Nobuo; Podjarny, Alberto (2008). «Neutron crystallography: opportunities, challenges, and limitations». Current Opinion in Structural Biology (en inglés) 18 (5): 593-600. doi:10.1016/j.sbi.2008.06.009.
- ↑ a b Center for Metalloenzyme studies. «X-Ray Crystallography» (en inglés). Archivado desde el original el 30 de octubre de 2012. Consultado el 19 de marzo de 2012.
- ↑ Ambrus, Attila. «Comparison of NMR and X-Ray Crystallography as Methods of the Protein Structure Determination» (en inglés). Consultado el 19 de marzo de 2012.
- ↑ Suneel, Sri D. «Special nano materials, characterization and Tools» (en inglés). Archivado desde el original el 2 de abril de 2012. Consultado el 19 de marzo de 2012.
- ↑ Garman, Elspeth F. (2010). «Radiation damage in macromolecular crystallography: what is it and why should we care?». Acta Crystallographica D (en inglés) 66: 339-351. doi:10.1107/S0907444910008656.
- ↑ Garman, Elspeth F. (2003). «'Cool' crystals: macromolecular cryocrystallography and radiation damage». Current Opinion in Structural Biology 13 (5): 545-551. PMID 14568608. doi:10.1016/j.sbi.2003.09.013.
Bibliografía[editar]
- Brindley, George W. y Brown, George, ed. (1980). Crystal structures of clay minerals and their X-ray identification (en inglés). Mineralogical Society. ISBN 0903056089.
- Drenth, Jan (1999). Principles of protein x-ray crystallography (en inglés) (2ª edición). Springer. ISBN 0387985875.
- Helliwell, John R. (1992). Macromolecular crystallography with synchrotron radiation (en inglés). Cambridge University Press. ISBN 0-521-33467-5.
- Luger, Peter (1980). Modern x-ray analysis on single crystals (en inglés). Walter de Gruyter. ISBN 3-11-006830-3.
- Stout, George H.; Jensen, Lyle H. (1989). X-ray structure determination — A practical guide (en inglés) (2ª edición). John Wiley & sons. ISBN 0-471-60711-8.































































































