Trisección del ángulo

La trisección del ángulo es uno de los tres problemas clásicos de la antigua matemática griega. El problema consiste en encontrar un ángulo cuya medida sea un tercio de otro ángulo dado, utilizando únicamente regla y compás.
El problema es sencillo en algunos casos (por ejemplo, si el ángulo dado es recto o si en el barrido por la circunferencia total puede construirse un ángulo que sea la tercera parte del mismo), pero es imposible de resolver en general, como demostró Pierre Wantzel en su artículo Recherches sur les moyens de reconnaître si un Problème de Géométrie peut se résoudre avec la règle et le compas, de 1837.[1] Su demostración utiliza la teoría de Galois.
La trisección del ángulo es uno de los problemas clásicos de la antigüedad griega que sobrevivió sin ser resuelto hasta el siglo XIX, junto con la cuadratura del círculo y la duplicación del cubo.[2] Este último fue resuelto en el mismo artículo por Wantzel, demostrando su irresolubilidad. La cuadratura del círculo también es imposible, como probó Carl Louis Ferdinand von Lindemann en 1882.
Es posible trisecar un ángulo arbitrario utilizando herramientas distintas a la regla y el compás. Por ejemplo, el método neusis, también conocido por los antiguos griegos, implica el deslizamiento y la rotación simultáneos de una regla graduada, lo que no se puede lograr con las herramientas originales. Los matemáticos desarrollaron otras técnicas en los siglos posteriores.
Debido a que el problema de la trisección del ángulo está definido en términos simples, pero es complejo hasta el punto de ser irresoluble, se convirtió en un tema frecuente de intentos pseudomatemáticos de resolución por parte de entusiastas ingenuos. Estas soluciones a menudo implican interpretaciones erróneas de las reglas o simplemente son incorrectas.[3]
Antecedentes y enunciado del problema[editar]

Usando solamente una regla sin marcar y un compás, los matemáticos griegos encontraron la manera de dividir una línea recta en un conjunto arbitrario de segmentos iguales, dibujar rectas paralelas, bisecar ángulos, construir algunos polígonos regulares y generar cuadrados de igual o dos veces el área de un determinado polígono.
Sin embargo, tres problemas específicos resultaron ser especialmente esquivos: trisecar un ángulo, duplicar un cubo y cuadrar un círculo. El problema de la trisección del ángulo se enuncia así:
|
Prueba de imposibilidad[editar]


Pierre Wantzel publicó una prueba de la imposibilidad de trisecar clásicamente un ángulo arbitrario en 1837.[4] La prueba de Wantzel, reformulada en terminología moderna, usa el álgebra abstracta de extensión de cuerpos, un tema que ahora se combina típicamente con la teoría de Galois. Sin embargo, Wantzel publicó estos resultados antes que Galois (cuyo trabajo se publicó en 1846) y no utilizó la conexión entre extensiones de cuerpos y grupos que es el tema específico de la teoría de Galois.[5]
El problema de construir un ángulo de una medida dada θ es equivalente a construir dos segmentos de manera que la razón de su longitud sea cos θ. De una solución a uno de estos dos problemas, se puede pasar a la solución del otro mediante una construcción con regla y compás. Existe una expresión trigonométrica que relaciona los cosenos del ángulo original y de su trisección:
- cos θ = 4 cos3 θ3 − 3 cos θ3
De ello se deduce que, dado un segmento que se define con una longitud unitaria, el problema de la trisección del ángulo es equivalente a construir un segmento cuya longitud es la raíz de un polinomio de tercer grado. Esta equivalencia reduce el problema geométrico original a un problema puramente algebraico.
Todo número racional es construible. Cada número irracional que es construible con regla y compás en un solo paso a partir de algunos números dados es una raíz de un polinomio de grado 2 con coeficientes en el cuerpo al que pertenecen estos números. Por lo tanto, cualquier número que se pueda construir mediante una secuencia finita de pasos es una raíz de un polinomio mínimo cuyo grado es una potencia de dos. El ángulo π3 radianes (60 grados, 60°) es construible. El siguiente argumento demuestra que es imposible construir un ángulo de 20°, lo que implica que no se puede trisecar un ángulo de 60° y, por lo tanto, que no se puede trisecar un ángulo arbitrario.
Denótese el conjunto de los números racionales por Q. Si se pudiera trisecar un ángulo de 60°, el grado de un polinomio mínimo de cos 20° sobre Q sería una potencia de dos. Ahora, considérese x = cos 20°. Se debe tener en cuenta que cos 60° = cos π3 = 12. Luego, por la fórmula del triple ángulo, cos π3 = 4x3 − 3x, e igualmente, 4x3 − 3x = 12.
Entonces, 8x3 − 6x − 1 = 0, y se define p(t) como el polinomio p(t) = 8t3 − 6t − 1.
Dado que x = cos 20° es una raíz de p(t), el polinomio mínimo para cos 20° es un factor de p(t). Debido a que p(t) tiene grado 3, si tiene solución en Q, entonces tiene una raíz racional. Según el teorema de la raíz racional, esta raíz debe ser ±1, ±12, ±14 o ±18, pero ninguna de ellas es una raíz del polinomio. Por lo tanto, p(t) es irreducible sobre Q, y el polinomio mínimo para cos 20° es de grado 3.
Por lo tanto, un ángulo de 60° no se puede trisecar.
Ángulos trisecables[editar]
Sin embargo, algunos ángulos se pueden trisecar. Por ejemplo, para cualquier ángulo constructible θ, un ángulo de medida 3θ se puede construir de forma trivial triplicando directamente un ángulo de medida θ. Hay ángulos que no son construibles pero que son trisecables (a pesar de que el ángulo de un tercio en sí mismo no es construible). Por ejemplo, 3π7 es un ángulo de este tipo: cinco ángulos de medida 3π7 se combinan para formar un ángulo de medida 15π7, que es un círculo completo más el π7 deseado.
Para un número natural N, un ángulo de medida 2πN es trisecable si y solo si 3 no divide a N.[6][7] En contraste, 2πN es construible si y solo si N es una potencia de 2 o el producto de una potencia de 2 con el producto de uno o más números de Fermat distintos.
Caracterización algebraica[editar]
Nuevamente, denótese el conjunto de los números racionales por Q.
Teorema: un ángulo de medida θ se puede trisecar si y solo si
- q(t) = 4t3 − 3t − cos(θ)
se puede reducir sobre la extensión del cuerpo Q(cos(θ)).
La demostración es una generalización relativamente sencilla de la prueba dada anteriormente de que un ángulo de 60° no es trisecable.[8]
Otros métodos[editar]
El problema general de la trisección de ángulos se puede resolver utilizando herramientas adicionales y, por lo tanto, saliendo del marco griego original de la regla y el compás.
Se han propuesto muchos métodos incorrectos para trisecar un ángulo en general. Algunos de estos métodos proporcionan aproximaciones razonables; otros (algunos de los cuales se mencionan a continuación) involucran herramientas no permitidas en el problema clásico. El matemático Underwood Dudley ha detallado algunos de estos intentos fallidos en su libro "The trisectors" (Los Trisectores).[3]
Método de construcción geométrica aproximada[editar]
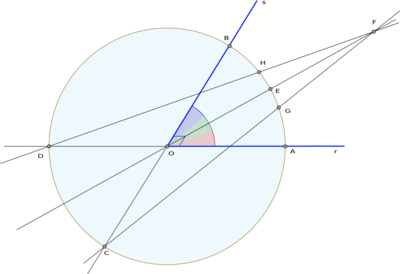
Esta construcción requiere trazar una circunferencia de radio arbitrario y con centro en el vértice O del ángulo a trisecar (∠AOB), y situar un punto F en la bisectriz del ángulo dado a una distancia del doble del radio de la circunferencia. Considerando ∠AOB = 2a y ∠HOG = 2x, entonces se tiene que el triángulo ΔOCF incluye el ángulo ∠OCF = ½ (a + x) ya que es un ángulo inscrito en la circunferencia que comprende un arco de medida a + x, y también se tiene que ∠CFO = ½ (a - x) porque al extender la bisectriz se obtiene un ángulo opuesto al ángulo ∠EOB = a, que por otro lado, es un ángulo externo al triángulo ΔOCF no adyacente a los ángulos ∠OCF = ½ (a + x ) y ∠CFO. En consecuencia:
Usando la ley de los senos y los cosenos en el triángulo ΔOCF y considerando los lados OF y OC que miden respectivamente 2.r y r, donde r es el radio de la circunferencia, entonces:
Con la segunda igualdad se llega a:
Dividiendo el numerador y el denominador del primer miembro de la expresión anterior, resulta: .
Esto demuestra que . De ello se deduce que x es aproximadamente .
Aproximación por bisecciones sucesivas[editar]


La trisección se puede aproximar mediante la repetición del método de la regla y el compás para bisecar un ángulo. Las series geométricas 13 = 14 + 116 + 164 + 1256 + ⋯ o 13 = 12 − 14 + 18 − 116 + ⋯ se pueden utilizar como base para las bisecciones. Se puede obtener una aproximación hasta cualquier grado de precisión en un número finito de pasos, pero la resolución exacta requeriría realizar un número infinito de pasos.[9]
Usando un acoplamiento mecánico[editar]
Un ángulo se puede trisecar con un dispositivo que es esencialmente una versión de cuatro brazos de un compás, con conexiones articuladas intermedias diseñadas para mantener iguales los tres ángulos entre los brazos adyacentes.[10] Este dispositivo fue estudiado por René Descartes en 1629, según consta en su correspondencia con Isaac Beeckman.[11]
Posteriormente, se idearían otros mecanismos simples capaces de trisecar ángulos, incluido el Trisector de Kempe y el mecanismo de abanico de Sylvester (también conocido como Isoklinostat).[12]
Usando origami[editar]

La trisección, como muchas construcciones imposibles con la regla y el compás, se puede lograr fácilmente mediante las operaciones de plegado de papel, u origami. Los axiomas de Huzita (tipos de operaciones de plegado) permiten construir extensiones cúbicas (raíces cúbicas) de longitudes determinadas, mientras que con la regla y el compás solo pueden construirse extensiones cuadráticas (raíces cuadradas).
La construcción en origami adjunta (ideada por de Hisashi Abe en 1980) ilustra el procedimiento:
- Se traza la línea d pasando por la esquina A de la hoja para que forme, con el borde inferior h0 de la hoja, el ángulo a cortar en tres.
- Se dobla la hoja para determinar dos bandas horizontales del mismo ancho (arbitrario) en la parte inferior de la hoja. Se denominan h1 y h2 a las líneas que las delimitan.
- Se dobla la hoja mediante un pliegue p para que AB delimite A'B', de manera que el punto A se sitúe sobre la línea h1 (generando el punto A'), al mismo tiempo que el punto B (intersección del borde izquierdo con la recta h2) se sitúe sobre la recta d, generando el punto B' (axioma 6 de las matemáticas del origami).
- La línea t que pasa por A y A' es entonces el trisector del ángulo dado: el ángulo formado por h0 y t es igual a 1/3 del ángulo formado entre h0 y d.
La demostración es simple: por simetría con respecto a la recta p, el punto medio P de AB da el punto medio P' de A'B' y, así como A'P es perpendicular a AB, se tiene que AP' es perpendicular a A'B'. Los dos triángulos rectángulos P'A'A y P'B'A son, por lo tanto, triángulos semejantes.
Por otro lado, sea H la proyección ortogonal de A' sobre h0. Dado que los triángulos HAA' y PA'A son semejantes como mitades del mismo rectángulo, y dado que los triángulos PA'A y P'AA' también son semejantes por simetría con respecto a P, se deduce que los triángulos HAA' y P'AA' son semejantes entre sí.
La semejanza de los tres triángulos HAA', P'AA' y P'AB' demuestra que las rectas AP' y AA' dividen el ángulo dAh0 en tres ángulos de la misma medida.
Con una escuadra triangular[editar]

En 1932, Ludwig Bieberbach publicó en el "Journal für die reine und angewandte Mathematik" su obra "Zur Lehre von den kubischen Konstruktionen".[13] Según sus propias palabras (traducción libre):
- "Como se sabe ... toda construcción cúbica se remonta a la trisección del ángulo y a la multiplicación del cubo, es decir, a la extracción de la tercera raíz. Solo pretendo demostrar cómo estas dos tareas clásicas se pueden resolver mediante el ajuste de un ángulo recto."
La siguiente descripción de la construcción (animación adyacente) contiene su continuación hasta la trisección completa del ángulo.
La construcción comienza con una circunferencia goniométrica alrededor del punto , el primer lado del ángulo a trisecar sobre el diámetro horizontal y a continuación un segundo círculo unitario alrededor de . Ahora, se traza un arco con radio igual al diámetro y centro en , que pasa por el punto . A continuación, se dibuja el segundo lado del ángulo , obteniéndose el punto . En el siguiente paso se utiliza el llamado "medio de construcción adicional", que en el ejemplo ilustrado es el "Geodreieck". El triángulo se debe colocar sobre el dibujo de la siguiente manera: el vértice del ángulo recto determina el punto sobre el lado del ángulo cuando un cateto del triángulo pasa por el punto y el otro es tangente al círculo unitario con centro en . Después se conecta el punto con y se dibuja la tangente desde al círculo unitario alrededor de (de acuerdo con el ajuste del ángulo recto mencionado anteriormente como Rechtwinkelhaken). El ángulo encerrado por los segmentos y es, por tanto, exactamente .
Para comprobarlo, se traza la paralela a desde , creando dos ángulos entre paralelas de valor y el punto . Una paralela adicional a desde determina el punto de contacto de la tangente con el círculo unitario alrededor de . Finalmente, si se traza una línea recta desde a través de hasta que se cruce con el círculo unitario en , se comprueba que el ángulo ha quedado dividido exactamente en tres partes.
Con una curva auxiliar[editar]
-
Trisección usando la espiral de Arquímedes
-
Trisección usando la trisectriz de Maclaurin
-
Trisección con el caracol de Pascal:
Hay ciertas curvas llamadas trisectrices que, si se dibujan en el plano usando otros métodos distintos de la regla y el compás, se pueden usar para trisecar ángulos arbitrarios.[14] Los ejemplos incluyen la trisectriz de Maclaurin, que en coordenadas cartesianas viene dada por la ecuación implícita
y la espiral de Arquímedes. De hecho, la espiral se puede utilizar para dividir un ángulo en "cualquier" número de partes iguales.
Con una regla graduada[editar]

Método de Arquímedes[editar]
Otro medio de trisecar un ángulo arbitrario con un "pequeño" paso fuera del marco clásico griego es mediante una regla con dos marcas separadas por una distancia determinada. La siguiente construcción se debe originalmente a Arquímedes. Este tipo de soluciones se caracterizan por utilizar el método neusis, incluyendo el empleo de herramientas distintas de un compás y de una regla no marcada. Los diagramas muestran esta construcción para un ángulo agudo, pero de hecho funciona para cualquier ángulo de hasta 180 grados.
La construcción implica asumir tres principios de la geometría euclídea:
- Cualquier conjunto completo de ángulos apoyados sobre una línea recta suma 180°,
- La suma de los ángulos de cualquier triángulo es 180°, y,
- Dos lados iguales de un triángulo isósceles encontrarán al tercero según el mismo ángulo (véase pons asinorum).
Construcción:
Sea l la línea horizontal en el diagrama adyacente. El ángulo a (a la izquierda del punto B) es el objeto de la trisección. Para ello, primero, se dibuja el punto A que delimita al ángulo a con el vértice en B, y a continuación se dibuja una circunferencia de radio AB. Entonces, entra en juego la regla en la que se ha marcado la distancia AB: mientras mantiene la regla (pero no la marca) pasando por A, la regla se desliza y gira hasta que una marca esté en la circunferencia y la otra en la recta l. La marca en el círculo figura como C y la marca en la recta está indicada como D. Esto asegura que CD = AB. Si se dibuja un radio BC, se hace evidente que los segmentos AB, BC y CD tienen todos la misma longitud. Ahora, los triángulos ABC y BCD son isósceles, por lo tanto (según el tercer principio), cada uno tiene dos ángulos iguales.
Hipótesis: Dado que AD es una línea recta, y que AB, BC y CD tienen la misma longitud,
Conclusión: Entonces el ángulo b = a3.
Demostración:
- Del Hecho 1) anterior, °.
- Mirando el triángulo BCD, del Hecho 2) °.
- De estas dos últimas ecuaciones, se deduce que .
- Del Hecho 2), °, entonces ° , y por lo tanto, ° .
- Del Hecho 1), °, luego ° °.
En consecuencia, (a − 3b = 0), o lo es lo mismo, (a = 3b), y el teorema queda demostrado.
Una vez más, el uso de una regla marcada hace que esta construcción quede fuera de las "reglas" de la matemática griega clásica, en la que solo se permitían construcciones con regla y compás exclusivamente.
Método de Nicomedes[editar]
El método de Nicomedes también se vale de una regla marcada para ajustar una longitud conocida.
Construcción:
Dado cualquier ángulo CÂB (véase la figura adjunta), se considera una recta , perpendicular a , que cruza en y a en . A continuación, por se traza una recta paralela a y por se traza una recta paralela a ; las rectas y se cruzan en . Ahora, desde se traza la recta , que se cruza con en y con en , ajustándola de forma que (véase método neusis):
- ; luego EÂD = CÂD.
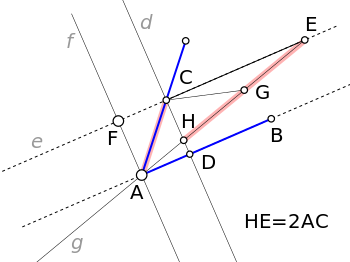
Demostración:
La construcción cumple las siguientes condiciones:
- CD AB
- FE//AD
- FA//CD
- EÂD CÂD
Sea el punto medio de , entonces se tiene que:
- por construcción
- porque el triángulo es rectángulo.
Y además, también se cumple que
Por otro lado
El ángulo CĜH es el ángulo externo del triángulo y, por lo tanto,
- CĜH EĈG + CÊG 2 CÊG
Pero también
De aquí se deduce que
- CÂB CÂG + GÂB 2 CÊG + GÂB 2 GÂB + GÂB 3 GÂB
y en consecuencia,
- GÂB CÂB como queda demostrado
Con una cuerda y un cilindro[editar]

Thomas Hutcheson publicó un artículo en el Mathematics Teacher[15] que usaba una cuerda en lugar de un compás y una regla. Una cuerda se puede utilizar como regla (estirándola) o como compás (fijando un punto e identificando otro), pero también se puede enrollar alrededor de un cilindro, la clave de la solución de Hutcheson.
Hutcheson construyó un cilindro a partir del ángulo a ser trisecado -dibujando un arco a través del ángulo, y completándolo como una circunferencia-, en la que se inscribe un triángulo equilátero para dividirla en tres partes iguales. A continuación, tras desarrollar el cilindro, procedía a proyectar estas tres partes iguales sobre el ángulo a ser trisecado mediante una simple construcción de triángulos semejantes. Tras devolver el cilindro a su posición original, los dos nuevos puntos generados se corresponden con la trisección del ángulo de partida.
Con un "tomahawk"[editar]

Un dispositivo trisector o "tomahawk" es una forma geométrica que consta de un semicírculo y dos segmentos ortogonales, de modo que la longitud del segmento más corto es igual al radio del círculo. La trisección se ejecuta apoyando el extremo del segmento más corto del tomahawk en uno de los segmentos del ángulo, y el borde del círculo en el otro, de modo que el "mango" (el segmento más largo) pase por el vértice del ángulo. Una vez ajustado el dispositivo trisector, una línea de trisección pasa por el vértice del ángulo y por el centro del semicírculo; y la otra coincide con el "mango" del aparato.
Aunque el "tomahawk" se puede construir con regla y compás, generalmente no es posible colocarlo en la posición que resuelve el problema utilizando exclusivamente estos dos elementos. En consecuencia, la construcción anterior no contradice la no trisectibilidad de los ángulos utilizando exclusivamente regla y compás.
El dispositivo produce el mismo efecto geométrico que el método de plegado de papel: la distancia entre el centro del círculo y la punta del segmento más corto es el doble de la distancia del radio, lo que siempre se cumple gracias a la que la circunferencia es tangente a uno de los lados del ángulo. También es equivalente al uso de una regla en L (una escuadra de carpintero).
Usos de la trisección angular[editar]

Un ecuación de tercer grado con coeficientes reales se puede resolver geométricamente con compás, regla y un trisector de ángulos si y solo si tiene tres raíces reales.[16]: Thm. 1
Un polígono regular con n lados se puede construir con regla, compás y un trisector de ángulos si y solo si donde r, s, k ≥ 0 y donde pi son primos distintos de 3 de la forma (es decir, son números primos de Pierpont mayores que 3).[16]: Thm. 2
Generalización[editar]
Para cualquier entero distinto de cero N, un ángulo de medida 2π⁄N radianes se puede dividir en n partes iguales con regla y compás si y solo si n es una potencia de 2 o es una potencia de 2 multiplicada por el producto de uno o más Fermat distintos. primos, ninguno de los cuales divide a N. En el caso de la trisección (n = 3, que es un número primo de Fermat), esta condición se convierte en el requisito mencionado anteriormente de que N no sea divisible por 3.[7]
Véase también[editar]
- Bisección
- Número construible
- Polígono construible
- Geometría euclidiana
- Historia de la geometría
- Teorema de Morley
- Cuadratriz
- Trisectriz
- Criptografía geométrica
- Otras construcciones imposibles con regla y compás:
Referencias[editar]
- ↑ M. L. Wantzel (1837). «Recherches sur les moyens de reconnaître si un Problème de Géométrie peut se résoudre avec la règle et le compas». Journal de Mathématiques Pures et Appliquées 1 (2): 366-372.
- ↑ Stillwell, John (2010). «Ruler and compass constructions». Mathematics andits history (en inglés) (Tercera edición). Springer. pp. 26-27. Consultado el 17 de julio de 2014.
- ↑ a b Dudley, Underwood (1994), The trisectors, Mathematical Association of America, ISBN 978-0-88385-514-0.
- ↑ Wantzel, P M L (1837). «Recherches sur les moyens de reconnaître si un problème de Géométrie peut se résoudre avec la règle et le compas.». Journal de Mathématiques Pures et Appliquées. 1 2: 366-372. Consultado el 3 de marzo de 2014.
- ↑ Para conocer la base histórica de la demostración de Wantzel en la obra anterior de Ruffini y Abel, y su sincronización respecto a Galois, véase Smorynski, Craig (2007), History of Mathematics: A Supplement, Springer, p. 130, ISBN 9780387754802..
- ↑ MacHale, Desmond. "Constructing integer angles", Mathematical Gazette 66, June 1982, 144–145.
- ↑ a b McLean, K. Robin (July 2008). «Trisecting angles with ruler and compasses"». Mathematical Gazette 92: 320-323. doi:10.1017/S0025557200183317. «See also Feedback on this article in vol. 93, March 2009, p. 156.»
- ↑ Stewart, Ian (1989). Galois Theory. Chapman and Hall Mathematics. pp. g. 58. ISBN 978-0-412-34550-0.
- ↑ Jim Loy (2003) [1997]. «Trisection of an Angle». Archivado desde el original el 25 de febrero de 2012. Consultado el 30 de marzo de 2012.
- ↑ Isaac, Rufus, "Two mathematical papers without words", Mathematics Magazine 48, 1975, p. 198. Reprinted in Mathematics Magazine 78, April 2005, p. 111.
- ↑ «Descartes’ Mathematics». Stanford Encyclopedia of Philosophy (en inglés). First published Mon Nov 28, 2011; substantive revision Fri Dec 11, 2015. Consultado el 23 de marzo de 2021.
- ↑ Yates, Robert C (1942). The Trisection Problem. The National Council of Teachers of Mathematics. pp. 39-42.
- ↑ Ludwig Bieberbach (1932) Zur Lehre von den kubischen Konstruktionen, Journal für die reine und angewandte Mathematik, H. Hasse und L. Schlesinger, Band 167 Berlin, p. 142–146 online-copie (GDZ). Retrieved on June 2, 2017.
- ↑ Jim Loy «Archived copy». Archivado desde el original el 4 de noviembre de 2013. Consultado el 4 de noviembre de 2013.
- ↑ Hutcheson, Thomas W. (May 2001). «Dividing Any Angle into Any Number of Equal Parts». Mathematics Teacher 94 (5): 400-405.
- ↑ a b c Gleason, Andrew Mattei (March 1988). «Angle trisection, the heptagon, and the triskaidecagon». The American Mathematical Monthly 95 (3): 185-194. JSTOR 2323624. doi:10.2307/2323624. Archivado desde el original el 5 de noviembre de 2014.
Lecturas relacionadas[editar]
- Courant, Richard, Herbert Robbins, Ian Stewart, "¿Qué son las matemáticas ?: una aproximación elemental a las ideas y métodos", Oxford University Press US, 1996. ISBN 978-0-19-510519-3.
Enlaces externos[editar]
- Sitio de MathWorld
- Problemas geométricos de la antigüedad, incluida la trisección de ángulos
- Un poco de historia
- Enlace con la construcción mediante una regla graduada
- Otro enlace, mencionando a Arquímedes
- Un artículo extenso con muchas aproximaciones y puntos de vista exteriores al ámbito griego
- sitio de geometría Archivado el 12 de enero de 2010 en Wayback Machine.
- Twelve Ways to Trisect an Angle – David Richeson en YouTube. (Doce maneras de trisecar un ángulo)
Otros medios de trisección[editar]
- Animación de la trisección aproximada de un ángulo, con un error máximo de ≈ ± 4E-8°
- Trisección mediante el caracol de Pascal (Archivado 2009-10-25) el caracol de Pascal de Pascal; véase también Trisectriz
- Trisección con la Espiral de Arquímedes
- Trisección mediante la concoide de Nicomedes
- Sitio sciencenews.org sobre el uso del origami
- Trisección hiperbólica y el espectro de los polígonos regulares





























































