Circunferencia circunscrita
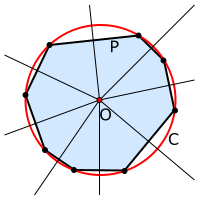
En geometría, la circunferencia circunscrita es la circunferencia que pasa por todos los vértices de un polígono y contiene completamente a dicha figura en su interior.[1] El centro de la circunferencia circunscrita se llama circuncentro[2][3] y su radio circunradio.[4][5]
Un polígono que tiene una circunferencia circunscrita se llama polígono cíclico.[6] Todos los polígonos simples regulares, todos los triángulos y todos los rectángulos son cíclicos. En todo polígono cíclico, el circuncentro se halla en el punto de intersección de las mediatrices de los lados del polígono.[3]
Circunferencia circunscrita de triángulos[editar]
Los triángulos son los únicos polígonos que tienen garantizado poseer una circunferencia circunscrita, ya que son siempre polígonos cíclicos. La única excepción son algunos triángulos degenerados que tienen superficie nula.
Circunferencia circunscrita de cuadriláteros[editar]

Los cuadriláteros inscritos poseen propiedades particulares, incluyendo que los ángulos opuestos son suplementarios que se deduce a partir de la generalización del arco capaz.
Véase también[editar]
Referencias[editar]
- ↑ «Circumcircle & Circumscribed Circle». Mathwords (en inglés). Consultado el 20 de febrero de 2012.
- ↑ «Circumcenter». Wolfram Mathworld (en inglés). Consultado el 3 de noviembre de 2015.
- ↑ a b Simmons, Bruce (2011). «Circumcenter». Mathwords (en inglés). Consultado el 20 de febrero de 2012.
- ↑ Simmons, Bruce (2011). «Circumradius». Mathwords (en inglés). Consultado el 20 de febrero de 2012.
- ↑ «Circumradius». Wolfram Mathworld (en inglés). Consultado el 3 de noviembre de 2015.
- ↑ >Weisstein, Eric W. «Polígono cíclico». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Enlaces externos[editar]
- Triángulo inscripto Sitio interactivo
- Circuncentro de un triángulo Sitio interactivo
