Ángulos suplementarios

Ángulos suplementarios.

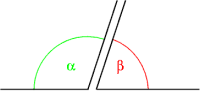
Dos ángulos son ángulos suplementarios si suman 180.

• Un ángulo es o tiene suplementario si es menor que $180^{\circ }$.

• El valor de $180^{\circ }$ es el mismo que dos ángulos rectos, $\pi$ rad o $200^{g}$ grados centesimales.
• Suplemento de un ángulo es lo que le falta al ángulo para medir un ángulo plano o llano.

Método de obtención

Aritmético

Para obtener el ángulo suplementario $\beta$ de un determinado ángulo $\alpha$, se restará $\alpha$ a $180^{\circ }$, de manera que:

$\beta =180^{\circ }-\alpha$

Propiedades

• Si dos ángulos son suplementarios de otros dos ángulos congruentes, también son congruentes entre sí.
• Los senos de los ángulos suplementarios son los mismos, por ejemplo:

$\operatorname {sen} \alpha =\operatorname {sen}(180^{\circ }-\alpha )$

$\operatorname {sen} \alpha =\operatorname {sen}(\pi -\alpha )$

$\operatorname {sen} 120^{\circ }=\operatorname {sen} 60^{\circ }$

• Los cosenos de los ángulos suplementarios son de igual valor absoluto, pero de signo inverso, como muestran los siguientes ejemplos:

$\cos \alpha =-\cos(180^{\circ }-\alpha )$

$\cos \alpha =-\cos(\pi -\alpha )$

$\cos 120^{\circ }=-\cos 60^{\circ }$

Véase también

Relaciones aritméticas entre ángulos:

• Ángulos congruentes
• Ángulos complementarios
• Ángulos conjugados

Relaciones posicionales entre ángulos:

• Ángulos adyacentes
• Ángulos consecutivos
• Ángulos opuestos por el vértice
• Ángulos interiores y exteriores

Determinados por dos paralelas y una transversal:

• Ángulos correspondientes
• Ángulos alternos

Ángulos:

• Ángulos

Enlaces externos

• Wikimedia Commons alberga una categoría multimedia sobre Ángulos suplementarios.

• Datos: Q1409132
• Multimedia: Supplementary angles / Q1409132