Polígono

tu mama me la lame

La palabra polígono deriva del griego antiguo πολύγωνος (polúgonos), a su vez formado por πολύ (polú) ‘muchos’ y γωνία (gōnía) ‘ángulo’,​​​ aunque hoy en día los polígonos son usualmente entendidos por el número de sus lados.

La noción geométrica elemental ha sido adaptada de distintas maneras para servir a propósitos específicos. A los matemáticos a menudo les interesan sólo las líneas poligonales cerradas y los polígonos simples (aquellos en los cuales sus lados sólo se intersecan en los vértices), y pueden definir un polígono de acuerdo a ello. Es requisito geométrico que dos lados que se intersecan en un vértice formen un ángulo no llano (distinto a 180°), ya que de otra manera los segmentos se considerarían partes de un lado único; sin embargo, esos vértices podrían permitirse algunas veces. En el ámbito de la computación, la definición de polígono ha sido ligeramente alterada debido a la manera en que las figuras son almacenadas y manipuladas en la computación gráfica para la generación de imágenes.

Línea poligonal

Se denomina línea poligonal al conjunto de segmentos unidos sucesivamente por sus extremos (el extremo de cada segmento es origen del siguiente), tal que dos segmentos sucesivos no están alineados (en tal caso se considera como un único segmento).​

Las líneas poligonales pueden ser abiertas o cerradas, un polígono está conformado por una línea poligonal cerrada.​

Elementos de un polígono

Hexágono regular.

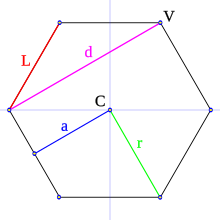
En un polígono se pueden distinguir los siguientes elementos geométricos:

• Lado (L): es cada uno de los segmentos que conforman el polígono.
• Vértice (V): es el punto de intersección (punto de unión) de dos lados consecutivos.
• Diagonal (d): es el segmento que une dos vértices no consecutivos.
• Perímetro (P): es la suma de las longitudes de todos los lados del polígono.
• Semiperímetro (SP): es la mitad del perímetro.
• Ángulo interior (AI): es el ángulo formado, internamente al polígono, por dos lados consecutivos.
• Ángulo exterior (AE): es el ángulo formado, externamente al polígono, por un lado y la prolongación de un lado consecutivo.
• Interior de un polígono es el conjunto de todos los puntos que están en el interior de la región que delimita dicho polígono. El interior es un abierto del plano.
• Exterior de un polígono es el conjunto de los puntos que no están en la poligonal (frontera) ni en el interior. El exterior es un abierto del plano.​
• Si el complemento (exterior) de una región poligonal es inconexo, este constará de varios fragmentos conexos llamados componentes. Uno y solo uno de los componente es ilimitado; todos los demás son limitados, a estos últimos se llaman huecos. Cada hueco con su frontera es un polígono.​

En un polígono regular se puede distinguir, además:

• Centro (C): es el punto equidistante de todos los vértices y lados.
• Ángulo central (AC): es el formado por dos segmentos de recta que parten del centro a los extremos de un lado.
• Apotema (a): es el segmento que une el centro del polígono con el centro de un lado; es perpendicular a dicho lado.
• Diagonales totales $N_{d}={\frac {n(n-3)}{2}}$, en un polígono de $n$ lados.
• Intersecciones de diagonales $N_{I}={\frac {n(n-1)(n-2)(n-3)}{24}}$, en un polígono de $n$ vértices.

Clasificación

Clasificación de polígonos según el número de lados
Nombre	n.º lados
trígono, triángulo	3
tetrágono, cuadrángulo, cuadrilátero	4
pentágono	5
hexágono	6
heptágono	7
octógono u octágono	8
eneágono o nonágono	9
decágono	10
endecágono o undecágono	11
dodecágono	12
tridecágono	13
tetradecágono	14
pentadecágono	15
hexadecágono	16
heptadecágono	17
octodecágono	18
eneadecágono	19
isodecágono, icoságono	20
triacontágono	30
tetracontágono	40
pentacontágono	50
hexacontágono	60
heptacontágono	70
octocontágono	80
eneacontágono	90
hectágono	100
chiliágono	1000
miriágono	10 000
decemiriágono	100 000
hectamiriágono, megágono	1 000 000
apeirógono	∞

Los polígonos se clasifican por el número de sus lados según la tabla adjunta, o bien por la forma de su contorno.

Polígono Simple Convexo Regular Irregular Cóncavo Complejo

Un polígono, por la forma de su contorno, se denomina

• Simple, si ningún par de aristas no consecutivas se corta. Equivalentemente, su frontera tiene un solo contorno.​
• Complejo, si dos de sus aristas no consecutivas se intersecan.
• Convexo, si tiene todos sus ángulos internos menores que 180º. O bien, si un segmento que une dos puntos cualesquiera del polígono yace en el interior de este.
• Cóncavo, si al atravesarlo una recta puede cortarlo en más de dos puntos; es el que tiene uno o varios ángulos mayores que 180º.
• Equilátero, si tiene todos sus lados iguales.
• Equiángulo, si tiene todos sus ángulos iguales.
• Regular, si es equilátero y equiángulo a la vez.
• Irregular, si tiene sus ángulos y lados desiguales.
• Cruzado es un polígono plano que tiene dos lados no consecutivos secantes.​ Por ejemplo una 'equis' que tiene unidos sus 'extremos' por dos lados que no se cortan.
• Ortogonal o isotético, si todos sus lados son paralelos a los ejes cartesianos $x$ o $y$.​
• Alabeado, si sus lados no están en el mismo plano.
• Estrellado, si se construye a partir de trazar diagonales en polígonos regulares. Se obtienen diferentes construcciones dependiendo de la unión de los vértices: de dos en dos, de tres en tres, etc.
• Reticular es simple y, al representarlo en un reticulado, cada vértice yace exactamente en un vértice de cuadrado unitario del reticulado (en este caso funciona la fórmula de Pick).​

• 
  Polígono simple, cóncavo e irregular.
• 
  Polígono complejo, cóncavo e irregular.
• 
  Polígono convexo y regular (equilátero y equiángulo).
• 
  Polígono estrellado.

Véase también

Figura geométrica Poliedro Politopo Regla y compás Anexo:Ecuaciones de figuras geométricas Triangulación de un polígono

Polígono regular Polígono equilátero Polígono construible Estrella (figura geométrica) Circunferencia circunscrita Teselación

Enlaces externos

• Wikimedia Commons alberga una categoría multimedia sobre Polígono.
• Los Polígonos en laslaminas.es (13/5/12)
• Weisstein, Eric W. «Polígono». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Polígono, en webdelprofesor.ula.ve
• Polígonos en YouTube.