Hexágono

Hexágono
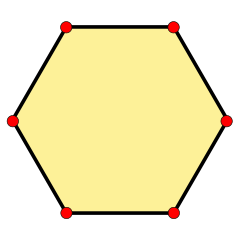	; Un hexágono regular
Características
Tipo	Polígono regular
Lados	6
Vértices	6
Grupo de simetría	, orden 2x6
Símbolo de Schläfli	{6}, t{3} (hexágono regular)
Diagrama de Coxeter-Dynkin	;
Polígono dual	Autodual
Área	; (radio )
Ángulo interior	120°
Propiedades
	Convexo, isogonal, cíclico
	[editar datos en Wikidata]

Un hexágono regular y sus ángulos principales

Hexágono irregular

En geometría plana elemental, un hexágono^[1]^[2] o exágono (esta última versión sin "h" está en desuso, ya no está recogida en la RAE) es un polígono de seis lados y seis vértices. Su nombre deriva del griego ἑξάγωνον (de ἕξ, "seis" y γωνία, "ángulo").

Propiedades[editar]

Un hexágono tiene:

6 vértices y lados.
9 diagonales.
La suma de los ángulos internos de un hexágono es 720 grados o $4\pi$ radianes.

Parhexágono[editar]

Siguiendo el hilo de un paralelogramo, un parhexágono o parexágono es aquel hexágono particular, en el que un lado es igual y paralelo a un lado opuesto, pero cada par de estos lados es de diferente tamaño.^[3]

Proposición[editar]

Sea ABCDEF un hexágono irregular cualquiera, se unen A con C; B con D; C con E; D con F; E con A; F con B. Se forman los seis triángulos ABC, BCD, CDE, DEF, EFA, FAB. En cada uno de ellos se localiza su baricentro; que se denotan como A', B', C', D', E', F'. Se unen sucesivamente dichos puntos, el hexágono A'B'C'D'E'F' es un parhexágono.^[4]

Hexágono regular[editar]

Medidas del hexágono regular

El hexágono regular es un polígono convexo con seis lados iguales y seis ángulos iguales, siempre dividido en triángulos simétricos o asimétricos.

El hexágono regular tiene las siguientes propiedades:

Sus ángulos internos son congruentes midiendo 120° o ${\frac {2\pi }{3}}$ rad. Resultado de $A_{i}={\frac {180(6-2)}{6}}$
Cada ángulo externo del hexágono regular mide 60° o ${\frac {\pi }{3}}$ rad.
Está íntimamente relacionado con los triángulos equiláteros:
- Uniendo cada vértice con su opuesto, el hexágono regular queda dividido en seis triángulos equiláteros.
- Numérense los vértices de 1 a 6 en el sentido horario. Uniendo los vértices impares se obtiene un triángulo equilátero; uniendo los vértices pares se obtiene otro.
Además de los cuadrados y los triángulos equiláteros, los hexágonos regulares congruentes (o iguales) son los terceros polígonos regulares que se pueden juntar para revestir totalmente una superficie plana sin dejar ningún vano.
Las seis raíces sextas de 1 o los números complejos que resuelven la ecuación $z^{6}-1=0$ están en los vértices de un hexágono regular ubicado en el plano complejo, siendo el primer vértice el punto (1,0).^[5]

Un hexágono regular es inscriptible y circunscribible en una circunferencia.Atendiendo a la figura, $r_{i}$ sería el radio del círculo inscrito, $r_{u}$ el radio del círculo circunscrito y $a$ la longitud de un lado. Caben las igualdades:^[6]

a=r_{u}

, la longitud de un lado es igual al radio del círculo circunscrito.

r_{i}=\cos(30^{\circ })r_{u}

, de esta forma se relacionan los radios de las circunferencias, entonces:

r_{i}={\frac {\sqrt {3}}{2}}r_{u}

y podemos concluir que

a=r_{i}={\frac {r_{u}}{2}}{\sqrt {3}}

Para una Hexágono regular de círculo circunscrito y longitud de lado

r_{u}=a=1

, el radio de la inscrita sería aproximadamente

r_{i}\approx 0.866

Las perpendiculares trazadas por los puntos medios del hexágono regular y las bisectrices de los ángulos internos del hexágono regular son ejes de simetría del mismo.^[7]

Perímetro[editar]

Su perímetro es seis veces la longitud de su lado.

P=n\cdot l_{n}=6\ l_{6}

, donde n es el número de lados y

l_{n}

, la longitud del lado.

El perímetro en función de la apotema ( $a_{p}$ ) es ^[8]

P=4\cdot a_{p}\cdot {\sqrt {3}}

Y en función del radio del círculo circunscrito ( $r_{u}$ ) es ^[8]

P=6\cdot r_{u}

Área[editar]

Área del hexágono regular

Si se conoce la longitud del apotema a₆ del polígono, una alternativa para calcular el área es:

A={\frac {P\cdot a_{p}}{2}}={\frac {6l_{6}\cdot a_{p}}{2}}=3l_{6}\cdot a_{p}

o

A=2{\sqrt {3}}\cdot a_{p}^{2}

Si solo conocemos el lado l₆ podemos calcular el área con la siguiente fórmula:

A=l_{6}^{2}{\frac {3{\sqrt {3}}}{2}}

, que equivale a las áreas de seis triángulos equiláteros que se obtienen al unir el centro con los seis vértices.

Construcción geométrica[editar]

Construcción geométrica de un hexágono regular.

Un hexágono regular puede construirse utilizando únicamente una regla y compás:

Dado un punto O cualquiera, trazar una circunferencia cuyo radio sea igual al lado del hexágono a construir;
Elegir un punto A sobre la circunferencia y trazar un diámetro que cruce O y A. Marcar el otro punto donde este diámetro interseca la circunferencia como D;
Apoyando el compás en el punto A, trazar un arco que cruce O, cortando a la circunferencia en dos puntos, marcados como B y F;
Apoyando el compás en el punto D, trazar un arco que cruce O, cortando a la circunferencia en dos puntos, marcados como C y E

Galería de hexágonos naturales y artificiales[editar]

La Francia continental o parte metropolitana de Francia recibe el sobrenombre de Hexágono (l'Hexagone en francés), por tener una forma vagamente hexagonal.
Los escudos del caparazón de una tortuga están conformados por hexágonos.
En el polo norte de Saturno se encuentra un patrón de nubes formando un hexágono.
El ajedrez hexagonal de Władysław Gliński.
Los pabellones de estilo chino en los jardines botánicos tienen una estructura hexagonal.
El hexágono es un teatro de arquitectura de tipo hexagonal ubicada en Reading, Reino Unido.
Un granero hexagonal.
Vista aérea del Parque nacional Tortugas Secas.
Ventana hexagonal de una casa.
Una imagen de burbujas ordenadas la una a la otra da la ilusión de ver hexágonos.
La hanksita, de uno de los muchos minerales del sistema cristalino hexagonal
Los panales están construidos con formas hexagonales.
$Columnas de basalto formadas naturalmente de la Calzada del Gigante en Irlanda del Norte; las masas grandes deben enfriarse lentamente para formar un patrón de fractura poligonal.$

Columnas de basalto formadas naturalmente de la Calzada del Gigante en Irlanda del Norte; las masas grandes deben enfriarse lentamente para formar un patrón de fractura poligonal.
La micrografía de un copo de nieve.
La estructura cristalina del Grafeno está formada por una rejilla de hexágonos.
El benceno, es un compuesto aromático con forma hexagonal.
Estructura cristalina de un hexágono molecular compuesto por anillos aromáticos hexagonales.
Segmentos de espejo E-ELT ensamblados.
El espejo del telescopio espacial James Webb, está compuesto por 18 segmentos hexagonales.

Véase también[editar]

Referencias[editar]

↑ Real Academia Española y Asociación de Academias de la Lengua Española (2005). «hexágono». Diccionario panhispánico de dudas. Madrid: Santillana. ISBN 978-8-429-40623-8.
↑ Real Academia Española. «hexágono». Diccionario de la lengua española (23.ª edición).
↑ Kasner- Newman. Matemáticas e maginación. Librería Hachete s.A., Buenos Aires (1944)
↑ Kasner-Newman. Op. cit.
↑ César A. Trejo. Variable compleja
↑ Edgar de Alencar Filho. Exercícios de geometría plana
↑ Pogorélov. Op. cit.
↑ ^a ^b Sapiña, R. «Calculadora del área y perímetro del hexágono regular». Problemas y ecuaciones. ISSN 2659-9899. Consultado el 20 de junio de 2020.

Enlaces externos[editar]

Wikimedia Commons alberga una categoría multimedia sobre hexágonos.
Wikcionario tiene definiciones y otra información sobre hexágono.

Datos: Q83043
Multimedia: Hexagons / Q83043

[1] Real Academia Española y Asociación de Academias de la Lengua Española (2005). «hexágono». Diccionario panhispánico de dudas. Madrid: Santillana. ISBN 978-8-429-40623-8.

[2] Real Academia Española. «hexágono». Diccionario de la lengua española (23.ª edición).

[3] Kasner- Newman. Matemáticas e maginación. Librería Hachete s.A., Buenos Aires (1944)

[4] Kasner-Newman. Op. cit.

[5] César A. Trejo. Variable compleja

[6] Edgar de Alencar Filho. Exercícios de geometría plana

[7] Pogorélov. Op. cit.

[pye-8] Sapiña, R. «Calculadora del área y perímetro del hexágono regular». Problemas y ecuaciones. ISSN 2659-9899. Consultado el 20 de junio de 2020.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]