Octodecágono
| Octodecágono | ||
|---|---|---|
 Un octodecágono regular | ||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 18 | |
| Vértices | 18 | |
| Grupo de simetría | , orden 2x18 | |
| Símbolo de Schläfli | {18}, t{9} (octodecágono regular) | |
| Diagrama de Coxeter-Dynkin |
| |
| Polígono dual | Autodual | |
| Área |
(lado ) | |
| Ángulo interior | 160° | |
| Propiedades | ||
| Convexo, isogonal, cíclico | ||
En geometría, un octodecágono u octadecágono es un polígono de 18 lados y 18 vértices.
Propiedades[editar]
Un octodecágono tiene 135 diagonales, resultado que se puede obtener aplicando la ecuación general para determinar el número de diagonales de un polígono, ; siendo el número de lados , tenemos:
La suma de todos los ángulos internos de cualquier octodecágono es 2880 grados o radianes.
Octodecágono regular[editar]
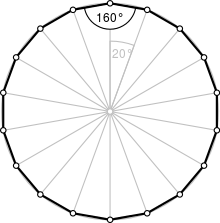
Un octodecágono regular es el que tiene todos sus lados de la misma longitud y todos sus ángulos internos iguales. Cada ángulo interno del octodecágono regular mide 160º u rad. Cada ángulo externo del octodecágono regular mide 20º o rad.
Al multiplicar la longitud t de un lado de un octodecágono regular por dieciocho (el número de lados n del polígono) obtendremos la longitud de su perímetro P.
El área A de un octodecágono regular con lado de longitud a se obtiene de la siguiente forma:
donde es la constante pi y es la función tangente calculada en radianes.
Si se conoce la longitud de la apotema a del polígono, otra alternativa para calcular el área es:
Construcción[editar]
Dado que 18=2×32, un octadecágono regular no puede ser construible usando solamente regla y compás.[1] Sin embargo, se puede construir usando el método neusis, o una trisección del ángulo con un dispositivo trisector.

La siguiente construcción aproximada es muy similar a la del eneágono, ya que un octadecágono puede construirse como un eneágono truncado. También es factible con el uso exclusivo de regla y compás.

|
Simetría[editar]

El octodecágono regular posee simetría diedral Dih18 de orden 36. Incluye 5 subgrupos de simetría diedrales: Dih9, (Dih6, Dih3) y (Dih2 Dih1), y 6 simetrías cíclicas: (Z18, Z9), (Z6, Z3) y (Z2, Z1). Las 15 clases de simetría se materializan en 12 tipos de formas de octodecágono distintas.
John Conway clasificó estas simetrías usando una letra y el orden de la simetría a continuación. Asignó la letra r al grupo de simetría de la figura regular; y en el caso de los subgrupos utilizó la letra d (de diagonal) para las figuras con ejes de simetría solo a través de sus vértices; p para figuras con ejes de simetría solo a través de ejes perpendiculares a sus lados; i para figuras con ejes de simetría tanto a través de vértices como a través de centros de lados; y g para aquellas figuras solo con simetría rotacional. Con a1 se etiquetan aquellas figuras con ausencia de simetría. Los tipos de simetrías más bajos permiten disponer de uno o más grados de libertad para definir distintas figuras irregulares.[2] Solo el subgrupo g18 no tiene grados de libertad, pero puede verse como un grafo dirigido. (Véase un ejemplo en la Teoría de grupos de John Conway)
![]()
Disección[editar]

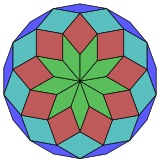
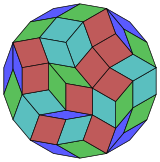
Harold Scott MacDonald Coxeter estableció que cada zonágono (un 2m-gono cuyos lados opuestos son paralelos y de igual longitud) se puede diseccionar en m(m-1)/2 paralelogramos.[3] En particular, esto es cierto para los polígonos regulares con muchos lados, en cuyo caso los paralelogramos son todos rombos. Para el octodecágono regular, m=9, y se puede dividir en 36, formando 4 conjuntos de 9 rombos. Esta descomposición se basa en una proyección con forma de polígono de Petrie de un eneracto, con 36 de sus 4608 caras. La lista A006245 enumera el número de soluciones como 112018190, incluidas rotaciones de hasta 18 veces y formas quirales en reflexión.

|

|
|

|
|
Uso[editar]
|
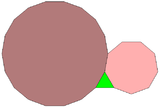
Un triángulo equilátero, y un nonágono y un octadecágono regulares, pueden rodear completamente un punto en el plano, una de las 17 combinaciones diferentes de polígonos regulares con esta propiedad.[4] Sin embargo, este patrón no se puede extender a un teselado arquimediano del plano: debido a que el triángulo y el nonágono tienen ambos un número impar de lados, ninguno de ellos puede estar completamente rodeado por un anillo alternando los otros dos tipos de polígono.
El octadecágono regular puede teselar el plano con espacios hexagonales cóncavos. Y otro mosaico se puede lograr mezclando nonágonos y huecos octogonales. El primer mosaico está relacionado con un teselado hexagonal truncado y el segundo con el teselado trihexagonal truncado.
Figuras relacionadas[editar]
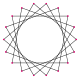
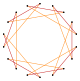
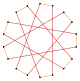
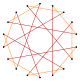
Un octodecagrama es un polígono en forma de estrella de 18 lados, representado por el símbolo {18/n}. Hay dos estrellas regulares: {18/5} y {18/7}, que utilizan los mismos puntos, pero conectan cada quinto o séptimo puntos. También hay cinco compuestos: {18/2} se reduce a 2{9} o dos eneágonos, {18/3} se reduce a 3{6} o tres hexágonos, {18/4} y {18/8} son reducidos a 2{9/2} y 2{9/4} o dos eneagramas, {18/6} se reduce a 6{3} o 6 triángulos equiláteros, y finalmente {18/9} se reduce a 9{2} como nueve dígonos.
Los truncamientos más profundos del eneágono regular y los eneagramas pueden producir formas de octodecagramas intermedios isogonales (figura isogonal) con vértices igualmente espaciados y dos longitudes de arista. Otros truncamientos forman recubrimientos dobles: t{9/8} = {18/8} = 2{9/4}, t{9/4} = {18/4} = 2{9/2}, t{9/2} = {18/2} = 2{9}.[5]
Polígonos de Petrie[editar]
El octodecágono regular es el polígono de Petrie para una serie de politopos de mayor dimensión, que se muestran en estos proyecciones oblicuas sobre el plano de Coxeter:
| Polígonos de Petrie octodecagonales | |||||||
|---|---|---|---|---|---|---|---|
| A17 | B9 | D10 | E7 | ||||
 símplex |
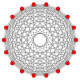 9-ortoplex |
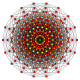 eneracto |
 711 |
 171 |
 321 |
 231 |
 132 |
Referencias[editar]
- ↑ Conway, John B. (2010), Mathematical Connections: A Capstone Course, American Mathematical Society, p. 31, ISBN 9780821849798..
- ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
- ↑ Harold Scott MacDonald Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
- ↑ Dallas, Elmslie William (1855), The Elements of Plane Practical Geometry, Etc, John W. Parker & Son, p. 134..
- ↑ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum
Bibliografía[editar]
Enlaces externos[editar]
 Wikimedia Commons alberga una categoría multimedia sobre octodecágonos.
Wikimedia Commons alberga una categoría multimedia sobre octodecágonos.- Weisstein, Eric W. «Octadecagon». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.