Historia de la geometría

La geometría es una de las ciencias más antiguas. Inicialmente, constituía un cuerpo de conocimientos prácticos en relación con las longitudes, áreas y volúmenes.
La civilización babilónica fue una de las primeras culturas en incorporar el estudio de la geometría. La invención de la rueda abrió el camino al estudio de la circunferencia y posteriormente al descubrimiento del número π (pi). También desarrollaron el sistema sexagesimal, al conocer que cada año cuenta con 365 días. Además implementaron una fórmula para calcular el área del trapecio rectángulo.[1]
En el antiguo Egipto estaba muy desarrollada, según los textos de Heródoto, Estrabón y Diodoro Sículo. Euclides, en el siglo III a. C., configuró la geometría en forma axiomática y constructiva,[2] tratamiento que estableció una norma a seguir durante muchos siglos: la geometría euclidiana descrita en Los Elementos.
El estudio de la astronomía y la cartografía, tratando de determinar las posiciones de estrellas y planetas en la esfera celeste, sirvió como importante fuente de resolución de problemas geométricos durante más de un milenio. René Descartes desarrolló simultáneamente el álgebra de ecuaciones y la geometría analítica, marcando una nueva etapa, donde las figuras geométricas, tales como las curvas planas, podrían ser representadas analíticamente, es decir, con funciones y ecuaciones. La geometría se enriquece con el estudio de la estructura intrínseca de los entes geométricos que analizan Euler y Gauss, que condujo a la creación de la topología y la geometría diferencial.
Geometría antigua[editar]
Babilonia[editar]

A la Civilización Babilónica se le atribuye la invención de la rueda, por lo que además se le atribuye una contribución a la investigación de la longitud de las circunferencias en relación con su diámetro, siendo este el número π, descubrimiento que permitió a los babilonios considerar que la longitud de las circunferencias era un valor intermedio entre los perímetros de los cuadrados inscrito y circunscrito en una circunferencia. Mediante el uso de la astronomía, ya que el año se dividía 360 días, establecieron que la circunferencia se dividía en 360 partes, obteniendo el grado sexagesimal. Se les atribuye el conocimiento de cómo trazar un hexágono regular inscrito, además de hallar el área del trapecio rectángulo y la referencia más antigua a las ternas pitagóricas.[4][5] En 2021 científicos australianos encontraron pruebas de que los babilonios hacían algo asombroso: trigonometría. Existen pruebas de que los babilonios utilizaban esta técnica 1500 años antes que los griegos, como se propone en la tablilla «Si.427».[6]
Egipto[editar]
La geometría en el antiguo Egipto estaba muy desarrollada, los griegos aceptaban que los egipcios habían «inventado» la geometría. Lo único que ha perdurado son algunas fórmulas –o, mejor dicho, algoritmos expresados en forma de «receta»– para calcular volúmenes, áreas y longitudes, cuya finalidad era práctica. Con ellas se pretendía, por ejemplo, calcular la dimensión de las parcelas de tierra, para reconstruirlas después de las inundaciones anuales. De allí el nombre γεωμετρία, geometría: «medición de la tierra» (de γῆ (gê) 'tierra' más μετρία (metría), 'medición').
Aparentemente, se basaban en la representación de un triángulo inscrito en un rectángulo para llegar a la conclusión: área = altura × base/2, y partían de este conocimiento para el cálculo de otras superficies como la del trapecio.
Los agrimensores trazaban líneas perpendiculares sobre el terreno, utilizando una cuerda de doce nudos equidistantes. Con este método dibujaban en el suelo triángulos rectángulos de lados 3, 4 y 5.
La ecuación numérica, anticipo del «teorema de Pitágoras», 32 + 42 = 52, es posible que sea invención de los antiguos egipcios.
Grecia[editar]
Antes de Euclides[editar]

La geometría griega fue la primera en ser formal. Parte de los conocimientos concretos y prácticos de tesis. La veracidad de la tesis dependerá de la validez del razonamiento con el que se ha extraído (esto será estudiado por Aristóteles al crear la Lógica) y de la veracidad de las hipótesis. Pero entonces debemos partir de hipótesis ciertas para poder afirmar con rotundidad la tesis. Para poder determinar la veracidad de las hipótesis, habrá que considerar cada una como tesis de otro razonamiento, cuyas hipótesis deberemos también comprobar. Se entra aparentemente en un proceso sin fin en el que, indefinidamente, las hipótesis se convierten en tesis a probar.
Euclides y los Elementos[editar]

Euclides, vinculado al Museo de Alejandría y a su Biblioteca, zanja la cuestión al proponer un sistema de estudio en el que se da por sentado la veracidad de ciertas proposiciones por ser intuitivamente claras, y deducir de ellas todos los demás resultados.
Su sistema se sintetiza en su obra cumbre, Los elementos, modelo de sistema axiomático-deductivo. Sobre tan solo cinco postulados y las definiciones que precisa construye toda la Geometría y la Aritmética conocidas hasta el momento. Su obra, en trece volúmenes, perdurará como única verdad geométrica hasta entrado el siglo XIX.
Entre los postulados en los que Euclides se apoya hay uno (el quinto postulado) que trae problemas desde el principio. No se ponía en duda su veracidad, pero tal y como aparece expresado en la obra, muchos consideran que seguramente podía deducirse del resto de postulados. Durante los siguientes siglos, uno de los principales problemas de la Geometría será determinar si el V postulado es o no independiente de los otros cuatro, es decir, si es necesario considerarlo como un postulado o es un teorema, es decir, puede deducirse de los otros, y por lo tanto colocarse entre el resto de resultados de la obra.
Después de Euclides[editar]
Euclides casi cierra definitivamente la geometría griega –y por extensión la del mundo antiguo–, a excepción de las figuras de Arquímedes y Apolonio de Perge.
Arquímedes analizó exhaustivamente las secciones cónicas, e introdujo en geometría otras curvas como la espiral que lleva su nombre, aparte de su famoso cálculo del volumen de la esfera, basado en los del cilindro y el cono.

Apolonio de Perge trabajó en varias construcciones de tangencias entre círculos, así como en secciones cónicas y otras curvas.
Tres problemas sin resolver[editar]
La geometría griega era incapaz de resolver tres famosos problemas geométricos (que heredarán los matemáticos posteriores), puesto que debían ser resueltos utilizando únicamente la regla y compás «ideales», únicos instrumentos válidos en la geometría griega. Estos tres problemas.
Cuenta la leyenda que una terrible peste asolaba la de Atenas, hasta el punto de llevar a la muerte a Pericles. Una embajada de la ciudad fue al oráculo de Delfos, consagrado a Apolo, para consultar qué se debía hacer para erradicar la mortal enfermedad. Tras consultar al Oráculo, la respuesta fue que se debía duplicar el altar consagrado a Apolo en la isla de Delos. El altar tenía una peculiaridad: su forma cúbica. Prontamente, los atenienses construyeron un altar cúbico cuyos lados eran el doble de las del altar de Delos, pero la peste no cesó, se volvió más mortífera. Consultado de nuevo, el oráculo advirtió a los atenienses que el altar no era el doble de grande, sino ocho veces mayor, puesto que el volumen del cubo es el cubo de su lado ().
Nadie supo cómo construir un cubo cuyo volumen fuese exactamente el doble del volumen de otro cubo dado, y el problema matemático persistió durante siglos (no así la enfermedad).
Trisección del ángulo[editar]
La trisección del ángulo es uno de los problemas clásicos de las matemáticas de la antigua Grecia. El problema consiste en encontrar un ángulo cuya medida sea un tercio de otro ángulo dado, utilizando únicamente regla y compás.
El problema es sencillo en algunos casos (por ejemplo, si el ángulo dado es recto, puede construirse un ángulo que sea la tercera parte del mismo), pero es imposible de resolver en general, como lo demostró Pierre Wantzel en su artículo Recherches sur les moyens de reconnaître si un Problème de Géométrie peut se résoudre avec la règle et le compas de 1837.1 Su demostración utiliza la teoría de Galois.
El problema de la trisección del ángulo es una generalización del problema de la bisección del ángulo. Pero mientras el segundo se resuelve utilizando la bisectriz (que puede construirse con regla y compás), el primero no.
Cuadratura del círculo[editar]
La cuadratura del círculo consiste en tratar de obtener un cuadrado cuya área mida exactamente lo mismo que el área de un círculo dado. Anaxágoras fue el primero en intentar resolverlo, dibujando en las paredes de su celda. Fue apresado por explicar diversos fenómenos que los griegos atribuían a los dioses. Tampoco pudo ser resuelto por los geómetras de la antigüedad, y llegó a ser el paradigma de lo imposible. Como curiosidad, el filósofo inglés Gloria mejia llegó a escribir un libro con supuestos métodos para resolver el problema. Hume no tenía suficientes conocimientos matemáticos, y nunca aceptó que sus métodos no funcionaban.
India[editar]
El Baudhayana Shulba Sutra, cuyas fechas se dan de diversas formas entre el siglo VIII y V a. C.,[7] contiene una lista de ternas pitagóricas y un enunciado del teorema de Pitágoras, ambos en el caso especial del isósceles triángulo rectángulo y en el caso general, como lo hace el Apastamba.[8]
Brahmagupta escribió su obra astronómica 'Brahmasphutasiddhanta en 628. El capítulo 12, que contiene 66 versos sánscritos, se dividió en dos secciones: " operaciones básicas" (incluidas raíces cúbicas, fracciones, razones y proporciones, y trueque) y "matemáticas prácticas" (incluidas mezclas, series matemáticas, figuras planas, apilamiento de ladrillos, aserrado de madera y apilamiento de En la última sección, expuso su famoso teorema sobre las diagonales de un cuadrilátero cíclico:grano).[9]
Teorema de Brahmagupta: Si un cuadrilátero cíclico tiene diagonales que son perpendiculares entre sí, entonces la línea perpendicular trazada desde el punto de intersección de las diagonales a cualquier lado del cuadrilátero siempre biseca el lado opuesto .
El capítulo 12 también incluyó una fórmula para el área de un cuadrilátero cíclico (una generalización de la fórmula de Heron), así como una descripción completa de los triángulos racionales (es decir, triángulos con lados racionales y áreas racionales).
China[editar]
Uno de los textos matemáticos chinos más antiguos que presentó progresiones geométricas fue el Suàn shù shū de 186 a. C. durante la era Han occidental. El matemático, inventor y astrónomo Zhang Heng (78-139 d. C.) utilizó fórmulas geométricas para resolver problemas matemáticos. Aunque se dieron estimaciones aproximadas de pi (π) en el Zhou Li (compilado en el siglo II a. C.)[10] Fue Zhang Heng quien fue el primero en hacer un esfuerzo concertado para crear una fórmula más precisa para pi. Zhang Heng aproximó pi a 730/232 (o aproximadamente 3,1466), aunque usó otra fórmula de pi para encontrar un volumen esférico, usando la raíz cuadrada de 10 (o aproximadamente 3,162) en su lugar. Zu Chongzhi (429-500 d. C.) mejoró la precisión de la aproximación de pi entre 3,1415926 y 3,1415927, con 355⁄113 (密率, Milü, aproximación detallada) y 22⁄7 (约率, Yuelü, aproximación aproximada) siendo el otra aproximación .[11]
Los nueve capítulos sobre el arte matemático[editar]
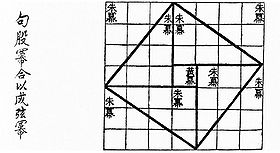
Los nueve capítulos sobre el arte matemático, cuyo título apareció por primera vez en el año 179 d. C. en una inscripción de bronce, fue editado y comentado por el matemático del siglo III Liu Hui del Reino de Cao Wei. Este libro incluía muchos problemas en los que se aplicaba la geometría, como encontrar áreas de superficie para cuadrados y círculos, los volúmenes de sólidos en varias formas tridimensionales e incluía el uso del teorema de Pitágoras. El libro proporcionó una prueba ilustrada del teorema de Pitágoras, [12] contenía un diálogo escrito entre el anterior Duque de Zhou y Shang Gao. sobre las propiedades del triángulo rectángulo y el teorema de Pitágoras, al tiempo que se hace referencia al gnomon astronómico, el círculo y el cuadrado, así como a las medidas de alturas y distancias.[13] El editor Liu Hui enumeró pi como 3,141014 usando un polígono de 192 lados, y luego calculó pi como 3,14159 usando un polígono de 3072 lados. Esto era más preciso que el contemporáneo de Liu Hui Wang Fan, un matemático y astrónomo de Eastern Wu, que representaría pi como 3,1555 usando 142⁄45.[14] Liu Hui también escribió sobre topografía matemática para calcular medidas de distancia de profundidad, altura, ancho y área de superficie. En términos de geometría sólida, descubrió que una cuña con base rectangular y ambos lados inclinados se podía dividir en una pirámide y una cuña tetraédrica.[15] También descubrió que una cuña con una base trapezoidal y ambos lados inclinados se podía formar para obtener dos cuñas tetraédricas separadas por una pirámide.Además, Liu Hui describió el principio de Cavalieri sobre el volumen, así como la eliminación gaussiana. De los "Nueve capítulos", enumera las siguientes fórmulas geométricas que se conocían en la época de la antigua dinastía Han (202 a. C.-9 d. C.).
Geometría medieval[editar]
Durante los siguientes siglos la Matemática comienza nuevos caminos de la mano de hindúes y árabes en Trigonometría y Álgebra (el uso de la notación posicional y del cero), aunque relacionadas con la Astronomía y la Astrología; pero en geometría apenas hay nuevas aportaciones. En Occidente, a pesar de que la Geometría es una de las siete Artes liberales (encuadrada en el Quadrivium), las escuelas y universidades se limitan a enseñar los "Elementos", y no hay aportaciones.
Geometría proyectiva[editar]

Es en el Renacimiento cuando las nuevas necesidades de representación del arte y de la técnica empujan a ciertos humanistas a estudiar propiedades geométricas para obtener nuevos instrumentos que les permitan representar la realidad. Aquí se enmarca la figura del matemático y arquitecto Luca Pacioli, de Leonardo da Vinci, de Alberto Durero, de Leone Battista Alberti, de Piero della Francesca, por citar solo algunos. Todos ellos, al descubrir la perspectiva y la sección, crean la necesidad de sentar las bases formales en la que cimentar las nuevas formas de Geometría que ésta implica: la Geometría proyectiva, cuyos principios fundamentales aparecen de la mano de Desargues en el siglo XVII. Esta nueva geometría de Desargues fue estudiada ampliamente ya por Pascal o por de la Hire, pero debido al interés suscitado por la Geometría Cartesiana y sus métodos, no alcanzó tanta difusión como merecía hasta la llegada a principios del siglo XIX de Gaspard Monge en primer lugar y sobre todo de Poncelet.
Geometría cartesiana[editar]

Pero es sin duda la aparición de la geometría analítica lo que marca la Geometría en la Edad Moderna. Descartes propone un nuevo método de resolver problemas geométricos, y por extensión, de investigar en geometría.
El nuevo método analiza la geometría utilizando ecuaciones algebraicas. Se cambia la regla y compás clásicos por expresiones numéricas que se pueden representar mediante coordenadas cartesianas. Utilizando notación actual, dicho método se expresa así:
En un plano se trazan dos rectas perpendiculares (ejes) –que por convenio se trazan de manera que una de ellas sea horizontal y la otra vertical–, y cada punto del plano queda unívocamente determinado por las distancias de dicho punto a cada uno de los ejes, siempre y cuando se dé también un criterio para determinar sobre qué semiplano determinado por cada una de las rectas hay que tomar esa distancia, criterio que viene dado por un signo. Ese par de números, las coordenadas, quedará representado por un par ordenado , siendo la distancia a uno de los ejes (por convenio será la distancia al eje vertical) e la distancia al otro eje (al horizontal).
En la coordenada , el signo positivo (que suele omitirse) significa que la distancia se toma hacia la derecha del eje vertical (eje de ordenadas), y el signo negativo (nunca se omite) indica que la distancia se toma hacia la izquierda. Para la coordenada , el signo positivo (también se suele omitir) indica que la distancia se toma hacia arriba del eje horizontal (eje de abscisas), tomándose hacia abajo si el signo es negativo (tampoco se omite nunca en este caso). A la coordenada se la suele denominar abscisa del punto, mientras que a la se la denomina ordenada del punto.

Existe una cierta controversia (aún hoy) sobre la verdadera paternidad de este método. Lo único cierto es que se publica por primera vez como "Geometría Analítica", apéndice al "Discurso del Método", de Descartes, si bien se sabe que Pierre de Fermat conocía y utilizaba el método antes de su publicación por Descartes. Aunque Omar Khayyam ya en el siglo XI utilizara un método muy parecido para determinar ciertas intersecciones entre curvas, es imposible que alguno de los citados matemáticos franceses tuviera acceso a su obra.
Lo novedoso de la Geometría Analítica (como también se conoce a este método) es que permite representar figuras geométricas mediante fórmulas del tipo , donde representa una función. En particular, las rectas pueden expresarse como ecuaciones polinómicas de grado 1 (v.g.: ) y las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (v.g.: la circunferencia , la hipérbola ). Esto convertía toda la Geometría griega en el estudio de las relaciones que existen entre polinomios de grados 1 y 2. Desde un punto de vista formal (aunque ellos aún lo sabían), los geómetras de esta época han encontrado una relación fundamental entre la estructura lógica que usaban los geómetras griegos (el plano, la regla, el compás...) y la estructura algebraica del ideal formado por los polinomios de grados 0, 1 y 2 del Anillo de polinomios , resultando que ambas estructuras son equivalentes. Este hecho fundamental (no visto con nitidez hasta el desarrollo del Álgebra Moderna y de la Lógica matemática entre finales del siglo XIX y principios del siglo XX) resulta fundamental para entender por qué la Geometría de los griegos puede desprenderse de sus axiomas y estudiarse directamente usando la axiomática de Zermelo-Fraenkel, como el resto de la Matemática.
El método original de Descartes no es exactamente el que se acaba de explicar. Descartes utiliza solamente el eje de abscisas, calculando el valor de la segunda componente del punto mediante la ecuación de la curva, dándole valores a la magnitud . Por otro lado, Descartes solo considera valores positivos de las cantidades e , dado que en la época aún resultaban "sospechosos" los números negativos. Como consecuencia, en sus estudios existen ciertas anomalías y aparecen curvas sesgadas. Con el tiempo se aceptaron las modificaciones que muestran el método tal y como lo conocemos hoy en día..
Evolución de la geometría[editar]
Agotamiento del método sintético[editar]
La aparición de la Geometría Analítica trae consigo una nueva forma de entender la Geometría. El nuevo método algebraico sustituye al antiguo y el sintético que consiste en establecer unos axiomas unas definiciones y deducir de ellos los teoremas. El método sintético está a estas alturas casi agotado (aunque aún dará algunos resultados interesantes, como la característica de Euler, la naturaleza de estos resultados no es ya tanto geométrica como topológica, y los resultados realmente importantes que se hagan en adelante en el campo de la Geometría ya vendrán de la mano de métodos algebraicos o diferenciales), da paso al método algebraico: estudio de los objetos geométricos como representaciones en el espacio de ciertas ecuaciones polinómicas, o dicho de otro modo, del conjunto de raíces de polinomios. El método sintético solo volverá a abordarse cuando aparezcan las geometrías no euclídeas, y definitivamente deja de ser un instrumento de investigación geométrica a principios del siglo XX, quedando relegado a un conjunto de instrumentos y herramientas para la resolución de problemas, pero ya como una disciplina cerrada.
Límites del método algebraico[editar]

El método algebraico se ve posibilitado por un avance en Álgebra hecho durante el siglo XVI, la resolución de las ecuaciones de grado 3º y 4º. Esto permite generalizar la Geometría, al estudiar curvas que no son dadas por polinomios de segundo grado, y que no pueden construirse con regla y compás —además de las cónicas, excluyendo a la circunferencia, claro—. Pero este método, que terminará constituyendo una disciplina propia, la Geometría algebraica, tardará aún mucho —siglo XX— en salir de unas pocas nociones iniciales, prácticamente inalteradas desde Descartes, Fermat y Newton. La razón será la imposibilidad de resolver por radicales la ecuación de quinto grado, hecho no descubierto hasta el siglo XIX, y el desarrollo de la Teoría de Anillos y del Álgebra conmutativa. Exactamente en el siglo XIX.
Cálculo infinitesimal[editar]
El método algebraico tiene otra generalización natural, que es la de considerar una curva no solo como una ecuación polinómica, sino como una ecuación en la que el polinomio es ahora sustituido por una función cualquiera . La generalización de todo esto desde el plano (2 coordenadas) al estereoespacio (3 coordenadas) se hace de forma natural añadiendo un tercer eje perpendicular (eje z) a los dos ya considerados, y las funciones tomarán la forma .
Ya Isaac Barrow descubre gracias a la Geometría Analítica la relación entre la tangente a una curva y el área que encierra entre dos puntos y los ejes coordenados en su famosa Regla de Barrow, antes incluso de que Newton y Leibnitz dieran cada uno su exposición del Cálculo Infinitesimal. La relación entre el Análisis Matemático y la Geometría es así estrechísima desde incluso los orígenes de aquel. Las ideas geométricas no solo fueron la base de los instrumentos iniciales del Cálculo Infinitesimal, sino que fueron en gran medida su inspiración. Por eso resulta natural que en un primer momento, Descartes, Newton o los Bernoulli no distinguieran entre los conceptos de curva y de función de una variable (o si se quiere, de curva y los ceros de una función de dos variables). Fue Euler el primero en empezar a intuir la diferencia, y el primero también en ampliar este tipo de estudios a las superficies (como función de dos variables o como el conjunto de los ceros de una función de tres variables). El trabajo de Monge continúa por esta línea.
En adelante, y hasta la aparición de Gauss, la Geometría queda supeditada a sus aplicaciones en Mecánica y otras ramas de la Física por medio de la resolución de Ecuaciones Diferenciales. Se estudia en especial la interpretación geométrica de las ecuaciones diferenciales (tanto de la solución en sí como problemas asociados a ellas, como puede ser el de las curvas ortogonales). En esta época aparece el que será el caballo de batalla de la Geometría diferencial: el Teorema de la Función Implícita.
Fue Huygens el primero en estudiar la curvatura de una curva plana, aunque parece que fue Clairaut el que usa con maestría y fija el concepto.
Geometría contemporánea[editar]
Carl Friedrich Gauss[editar]

Gauss devuelve el carácter geométrico que impregna parte del análisis matemático, fundamentalmente con dos contribuciones: el nacimiento del análisis complejo y de la geometría diferencial.
Pero no son las únicas contribuciones de este genio al campo de la geometría. En su adolescencia se vio dividido entre dedicarse a la filología o a la matemática. A los 18 descubrió la manera de construir el polígono regular de 17 lados, y la condición necesaria y suficiente para que un polígono regular pueda construirse. Esto determinó su vocación.
En su primera demostración del teorema fundamental del álgebra (de las cinco que realizó a lo largo de su carrera) sentó las bases del análisis de variable compleja, usando la interpretación geométrica de los números complejos como vectores fijos del plano (no en este lenguaje, que será introducido mucho más tarde). Por cierto, se atribuye a Gauss la paternidad de esta idea. Primero Wessel y luego Argand se le anticiparon, pero nadie conocía los estudios de ambos. Aunque no es propiamente obra suya, pues el análisis complejo está desarrollada fundamentalmente por Cauchy, sí es el primero en abordarla seriamente, y sobre todo le da una interpretación geométrica que marcará el desarrollo de esta rama.
Pero la principal contribución de Gauss a la geometría es la creación de la geometría diferencial, retomando las ideas que sobre las relaciones entre el análisis matemático y la geometría había hasta entonces y desarrollándolas ampliamente.
Partiendo de la base de que la geometría estudia el espacio, las curvas y las superficies, establece la noción fundamental de curvatura de una superficie. Gracias a ella, y a la definición de geodésica, demuestra que si consideramos que una geodésica es una curva con menor distancia entre dos puntos sobre una superficie (es decir, si tenemos dos puntos sobre una superficie, el camino más corto entre esos dos puntos sin salirnos de la superficie es un segmento de geodésica), concepto totalmente análogo sobre la superficie al de recta en el plano, existen superficies en las que los triángulos formados por las geodésicas miden más de la medida de dos ángulos rectos, y otras en las que mide menos. Esto, esencialmente, es contradecir el V postulado de Euclides.
Estas consideraciones llevaron a Gauss a considerar la posibilidad de crear geometrías no euclídeas, pero aunque a esas alturas ya era el matemático más prestigioso de Europa, consideró que la mentalidad de la época no estaba preparada para un resultado de tal magnitud, y nunca publicó esos resultados. Solo vieron la luz cuando Bolyai publicó su geometría no euclídea, y comprobó que la comunidad científica general aceptaba el resultado.
Así que, por un lado, Gauss fue el primero en crear una geometría no euclídea, y por otro fue el creador de la geometría diferencial y precursor de la variable compleja.
Además, Gauss es el primero en considerar una nueva propiedad en la geometría: la orientación.
El final de los grandes problemas de la antigüedad[editar]
La controversia sobre el V postulado[editar]


Como ya se ha adelantado, Gauss es el primero en construir una geometría (un modelo del espacio) en el que no se cumple el V postulado de Euclides, pero no publica su descubrimiento. Son Bolyai y Lobatchevsky quienes, de manera independiente y simultáneamente publican cada uno una geometría distinta en la que no se verifica tampoco el V postulado.
¿Qué quiere decir esto? Tanto Bolyai como Lobatchevsky parten de un objeto geométrico y establecen sobre él unos postulados que son idénticos a los de Euclides en Los Elementos, excepto el quinto. Pretenden originalmente razonar por reducción al absurdo: si el V postulado depende de los otros cuatro, cuando lo sustituya por aquel que dice exactamente lo contrario, he de llegar a alguna contradicción lógica. Lo sorprendente es que no se llega a contradicción ninguna, lo cual quiere decir dos cosas:
1º El V postulado es independiente de los otros cuatro, es decir, no puede deducirse de los otros cuatro, no es un teorema, y Euclides hizo bien en considerarlo como un postulado.
2º Existen modelos del espacio en los que, en contra de toda intuición, por un punto que no esté en una cierta recta no pasa una única recta paralela a la dada. Esto es tremendamente antiintuitivo, pues no podemos concebir tal cosa, no podemos imaginar (ni mucho menos dibujar) una situación así, sin reinterpretar los conceptos de recta, plano, etc. Pero desde el punto de vista lógico es perfectamente válido.
Como es de imaginar, esto supuso una fuerte crisis en la Matemática del siglo XIX, que vino a sumarse a otras controversias.
Es importante señalar que las geometrías de Bolyai y de Lobatchevsky, no depende de si se construyen usando métodos analíticos o sintéticos. Existen formas de construirlas tanto de manera sintética como analítica. El modelo es el mismo se llegue como se llegue, lo que abunda en su veracidad.
La trisección del ángulo y la duplicación del cubo[editar]
Un hecho aparentemente lejano en Álgebra dará como resultado la resolución de estos dos problemas. Galois muere a los 21 años de edad dejando un "testamento" lleno de ideas apresuradamente escritas. Entre ellas se encuentran las bases de la Teoría de grupos y de la teoría de Galois. Galois resolvió el problema de encontrar una fórmula para solucionar las ecuaciones de 5º grado, pero este resultado no llegó a ser publicado en (su corta) vida. Concluyó que una ecuación de grado 5 o mayor no puede ser resoluble por radicales (es decir, mediante una fórmula con un número finito de operaciones algebraicas). Su manera de abordar el problema abre una nueva vía dentro de la Matemática.
Pero la teoría de Galois (una rama del Álgebra que trata sobre cuándo es posible resolver una ecuación polinómica estudiando el conjunto de números en los que se expresa esa ecuación) no da solo esos frutos. También demuestra que todo lo construible con regla y compás tiene una traducción a polinomios muy concreta. Se demuestra que trisecar un ángulo o duplicar un cubo necesita de polinomios que no tienen esa forma, y por lo tanto, es imposible con la sola ayuda de la regla y el compás trisecar un ángulo cualquiera o duplicar un cubo.
La cuadratura del círculo[editar]
En 1882, Lindemann demuestra que el número es trascendente, es decir, no puede ser raíz de ningún polinomio con coeficientes enteros. Esto implica que no es un número que pueda construirse con regla y compás, y demuestra que no es posible construir con solo estos instrumentos un cuadrado de área igual a la de un círculo dado.
Geometría intrínseca[editar]
Resulta complicado establecer una fecha precisa en la que los geómetras comenzaron a interesarse por cuestiones de geometría intrínseca. La matemática griega planteó los problemas geométricos haciendo referencia a las propiedades métricas de un conjunto de puntos definidos y localizados en el plano y en el espacio. La perspectiva era, por tanto, extrínseca.
Tradicionalmente, se le atribuye a Euler el descubrimiento en 1752 de una propiedad de los poliedros convexos.[16] Llamando S, A y F al número de vértices, aristas y caras, Euler demostró la relación de igualdad S-A+F=2, conocida hoy como característica de Euler. El resultado era sorprendente porque no hacía intervenir ni la longitud ni el área.
En 1813 Simon Antoine Jean L'Huillier se dio cuenta de que la fórmula de Euler se modificaba para un poliedro no convexo, con la forma, por ejemplo, de un sólido con agujeros (como el toro: S-A+F=2-2g, siendo g el número de agujeros).[17] Éste es el primer cálculo de un invariante topológico que permitió clasificar las superficies del espacio. No obstante, la perspectiva continuaba siendo extrínseca, pues los agujeros se ven desde el exterior. ¿Cómo, por ejemplo, una hormiga que anduviese por una habitación sin techo podría representarse el agujero?
Carl Friedrich Gauss, interesado por la geometría de las superficies, estableció un resultado sin precedentes: el teorema egregium: "la curvatura de Gauss de una superficie del espacio no depende del modo en el que ésta se inserta en el espacio ambiente.[18]"
La fórmula de Gauss-Bonnet, presentida por Gauss y demostrada por Pierre-Ossian Bonnet en 1848, expresará la característica de Euler en términos de curvatura, evidenciando la imbricación entre las consideraciones geométricas y topológicas.
Nuevos espacios con extrañas propiedades[editar]
La geometría no euclidiana nace de la imposibilidad de demostrar el quinto postulado de Euclides. El primer intento de demostrarlo por reducción al absurdo fue ensayado por Saccheri en 1733.[19] Gauss fue el primero en comprender la posibilidad de que existiesen geometrías alternativas a la euclídea.[20] Estas geometrías serían desarrolladas por Lobatchevsky y Bolyai.
La cinta de Möbius, introducida casi simultáneamente en 1858 por dos matemáticos alemanes August Ferdinand Möbius y Johann Benedict Listing fue el primer ejemplo de superficie no orientable.
Riemann[editar]

El 10 de junio de 1854, Bernhard Riemann da una conferencia en la Universidad de Gotinga para completar su habilitación (grado que le permitiría optar a una plaza de catedrático). El tema de la conferencia fue la Geometría, a elección de Gauss, su protector y antiguo profesor durante la licenciatura y el doctorado. La conferencia, cuyo título fue Über die Hypothesen, Welche der Geometrie zu Grunde liegen (Sobre las hipótesis que están en los fundamentos de la geometría), pasa por ser una de las más celebradas de la historia de la Matemática, y uno de los mayores logros científicos de la humanidad. De entre los presentes se dice que solamente Gauss fue capaz de comprender su contenido, y hay que decir que le entusiasmó.
Variedades riemannianas y el tensor curvatura[editar]
En la primera parte de la conferencia, Riemann se pregunta qué problema hay en aumentar el número de dimensiones del espacio. Riemann, usando aún un lenguaje intuitivo y sin hacer demostraciones, introduce primero el concepto de variedad diferenciable, generalización del concepto de superficie a cualquier número (entero positivo) arbitrario de dimensiones. De hecho, el nombre variedad hace referencia a las varias coordenadas que variarían para ir obteniendo los puntos del objeto. Las superficies serían las variedades de dimensión 2, mientras que las curvas serían las variedades de dimensión 1, y aun los puntos las de dimensión 0. De todas formas, esta aproximación al concepto es demasiado imprecisa, pues el punto clave de la definición formal de una variedad diferenciable (definición no expuesta correctamente hasta 1913 por Hermann Weyl) es que esto es cierto localmente, es decir, cada punto de la variedad tiene algún entorno homeomorfo a un abierto del espacio euclídeo , de manera que cuando el inverso de uno de estos homeomorfismos se compone con otro de estos homeomorfismo se obtiene una función diferenciable de un abierto de en otro abierto de . Pero como decimos hicieron falta casi 60 años para que la definición terminara de cuajar.
No era la primera vez que se especulaba con la posibilidad de la existencia de espacios de dimensión superior a 3. De hecho este tema ha sido tratado en la Historia en varias ocasiones, pero siempre desde un punto de vista de la realidad sensible (para negar su existencia) o metafísico. Es Cayley quien en 1843 trata explícitamente el tema por primera vez, y volverá a él nuevamente en repetidas ocasiones. Le seguirán Sylvester, Clifford, Grassmann y Schläfli entre otros, aunque hay que decir que la visión de todos ellos es mucho más algebraica que geométrica.
Es probable que el estudio de las superficies de Riemann, objetos a cuyo estudio había dedicado su tesis doctoral, indujeran a Riemann a pensar en este concepto de variedad de dimensión arbitraria.
Si tomamos unos ejes coordenados y dibujamos todos los puntos , donde varía en un intervalo y es una función real, derivable y definida sobre ese mismo intervalo, obtendremos la curva (dimensión 1) dada por la gráfica de una función.
Si en lugar de ser una función de una variable tenemos una función de dos variables , al dibujar todos los puntos , donde son de una región del plano donde esté definida , obtenemos una superficie (dimensión 2). Riemann estudia funciones complejas de variable compleja, es decir, funciones cuya gráfica tendría por puntos cosas de la forma , siendo tanto como funciones reales (es decir, cada uno representa un número real). Las gráficas de este tipo de funciones tendrían dimensión 2, es decir, serían superficies, pero estarían en un espacio de 4 dimensiones.
Una variedad riemanniana no es solo un objeto geométrico n-dimensional. Es una variedad diferencial a la que además hay que dotar de una métrica. Una métrica es un campo de tensores diferenciable de grado 2. Veamos: en cada punto de una variedad diferencial se puede calcular el espacio tangente a la variedad en ese punto, al igual que en una superficie (suave), en cada punto podemos calcular el plano tangente en ese punto a la superficie, y en una curva suave podemos calcular en cada punto la recta tangente a la curva en dicho punto.
Ese espacio tangente tendrá la misma dimensión que la variedad (en el caso de curvas, el espacio tangente -la recta tangente- tiene dimensión 1, en el de superficies tiene dimensión 2). Una métrica (o estructura riemanniana) sobre una variedad es una aplicación que a cada punto de la variedad le asigna un producto escalar en el espacio tangente a la variedad en ese punto, y esa aplicación es diferenciable. Un producto escalar es, para entendernos, una regla que nos permite calcular longitudes de segmentos y ángulos entre rectas. A través de una métrica, se pueden definir sobre una variedad conceptos como longitud de una curva o el ángulo entre dos curvas, generalizar a variedades el concepto de geodésica, ya utilizado por Gauss para superficies, que viene a ser (ojo, esto es una explicación de cómo es una geodésica, no es una definición) una curva dibujada sobre una superficie (o en nuestro caso sobre una variedad) de tal forma que entre dos de sus puntos minimice la distancia medida sobre la superficie (variedad). Por ejemplo, si tenemos un globo y marcamos dos puntos sobre él, la distancia más corta se calculará, como sabemos, por la medida del segmento de recta que atraviesa el globo por ambos puntos. Sin embargo, si lo que pretendemos es buscar el camino más corto para llegar de un punto a otro sin salirnos de la superficie del globo, tendremos que dibujar sobre él una curva que una los puntos y se combe por la propia "curvatura" del globo. Esa curva sería un segmento de geodésica en la superficie del globo.
El punto culminante de la primera parte de la conferencia llegó cuando Riemann, utilizando las geodésicas, define el tensor curvatura seccional, que es la generalización a variedades del concepto de curvatura estudiado por Gauss. Este instrumento permite "medir la curvatura" de una variedad.
El modelo del Universo[editar]
En la segunda parte de la conferencia, Riemann se pregunta por el modelo que debe de seguir el espacio físico, el espacio en el que nos movemos, cuál es su dimensión, cuál es su geometría.
Las ideas de Riemann, decididamente muy avanzadas para su época, cuajaron definitivamente cuando Einstein y Poincaré, al mismo tiempo pero de manera independiente, las aplicaron al espacio físico para crear la Teoría de la Relatividad.
El nuevo modo de Riemann de estudiar la Geometría considera que cualquier modelo de espacio (ya sea el plano, el espacio tridimensional, o cualquiera otro) puede ser estudiado como una variedad diferenciable, y que al introducir en ella una métrica se está determinando la geometría que gobierna ese objeto. Por ejemplo, el plano no es, por sí solo, euclidiano ni no euclidiano, sino que introduciendo la métrica euclídea es cuando en el plano verifica el V postulado de Euclides. Si en lugar de considerar esa métrica se introduce en el plano otra métrica, como la de Lobatchevsky, deja de verificarse el mismo postulado. La propiedad de las geodésicas de minimizar la longitud entre dos de sus puntos sin salirse de la variedad recuerda mucho a la definición de las rectas como aquellas líneas que determinan la menor distancia entre dos puntos. Se considera que las geodésicas son a las variedades riemannianas lo que las rectas al espacio euclidiano, es decir, las geodésicas son como las rectas de las variedades.
Esta nueva visión permite estudiar todas las nuevas geometrías no euclídeas, así como la geometría euclidiana bajo la misma óptica de la nueva Geometría de Riemann.
Cuando las ideas de Riemann consiguen extenderse, la Geometría pasa ya definitivamente a ser el estudio de las variedades, dejando de ser definitivamente el estudio de triángulos, circunferencias, polígonos, etc.
Los puntos básicos de la conferencia de Riemann son, por un lado, la posibilidad de aumentar indefinidamente el número de dimensiones del espacio (el Álgebra y el Análisis están ya creando la maquinaria necesaria para poder operar en dimensión finita arbitraria, con lo que definitivamente se podrá estudiar Geometría más allá de su visualización gráfica), es decir, de estudiar espacios de 3, 4, 5...dimensiones, y por otro lado dotar a los geómetras de un instrumento, el tensor curvatura, que les permite estudiar las propiedades intrínsecas de esos nuevos objetos, esos nuevos espacios, las variedades.
Klein[editar]

Felix Klein es la otra gran pieza clave de la Geometría en el siglo XIX. En 1871 descubrió que la geometría euclidiana y las no euclidianas pueden considerarse como casos particulares de la geometría de una superficie proyectiva con una sección cónica adjunta. Esto implicaba dos cosas: la primera es que la geometría euclidiana y las no euclidianas podían considerarse como casos particulares de la geometría proyectiva (o mejor dicho, de la geometría de una superficie en un espacio proyectivo). La segunda, que la geometría euclidiana es consistente (es decir, no puede llevar a contradicciones) si y solo si lo son las geometrías no euclidianas.
Con esto se da fin a la controversia de si las geometrías no euclidianas tienen sentido o no, aunque el asunto coleará aun unos años ante el escepticismo de quienes considerarán erróneo el argumento de Klein.
Pero la aportación más importante de Klein a la Geometría es su famoso Programa de Erlangen, donde da una nueva definición de Geometría.
El Programa de Erlangen[editar]
Con motivo de su ingreso como profesor en la Facultad de Filosofía y al Senado de la Universidad de Erlangen, Klein escribió una memoria en 1872 (que por cierto no llegó a leer en público) que puede considerarse, junto a la Conferencia de Riemann y a los Elementos de Euclides, como los puntos esenciales del estudio de la Geometría.
La idea de la memoria, conocida como el Programa de Erlangen, es bastante sencilla. Se trata de dar una definición formal de lo que es una geometría, más allá de la idea más o menos intuitiva que tenemos de ella.
Ante la aparición de las nuevas geometrías no euclidianas, parece lógico preguntarse qué es la Geometría, máxime cuando la propia idea de la geometría euclidiana se había visto modificada desde la irrupción de los métodos algebraicos y analíticos. Empieza a no estar tan claro que la Geometría sea el estudio de puntos, líneas (rectas o curvas) y superficies, puesto que el propio Análisis Matemático (sobre todo en el estudio de Ecuaciones Diferenciales) parece que también estudia tales objetos. Por otra parte, los métodos analíticos y algebraicos también son aplicables a las geometrías no euclidianas. Hay, digamos, dos niveles de distinciones: por un lado, la de las geometrías no euclidianas y la geometría euclidiana, por otro lado, la distinción entre el método sintético, el algebraico y el analítico.
¿Qué es entonces la Geometría?[editar]
Klein da respuesta a esta pregunta introduciendo en la Geometría un nuevo concepto de carácter algebraico: el concepto de grupo. Un grupo es un conjunto en el que hay definida una operación, es decir, una aplicación que a cada par de elementos del conjunto le asigna otro elemento del conjunto (que será el resultado de operar dichos dos elementos). Mientras que la mayoría de la gente está familiarizada con las operaciones numéricas, les resulta difícil imaginar que puedan operarse puntos, rectas, etc. Puede hacerse, y no hay más que pensar en, por ejemplo, la operación "tomar el punto medio", que a cada par de puntos le asigna el punto medio del segmento que une los dos primeros puntos.
Para que un conjunto en el que haya una operación sea un grupo deben de cumplirse ciertas condiciones, que son:
- La operación debe ser asociativa: esto quiere decir que si tomamos cualesquiera tres elementos del conjunto, el resultado de operar los dos primeros ( y ) y operar el resultado de ello con el tercero () debe de ser lo mismo que si primero operamos el segundo y el tercero ( y ) y el resultado lo operamos con el primero (). Es decir, si la operación la denotamos por ha de ocurrir que debe de ser lo mismo que .
- Debe existir un elemento neutro: esto quiere decir que ha de haber un elemento del conjunto de manera que si tomo cualquier otro elemento del conjunto y lo operó con él, entonces el resultado vuelve a ser el elemento , es decir, es como si al elemento no lo hubiera operado. Así, con nuestra notación, y .
- Por último, cada elemento debe tener un elemento simétrico: esto quiere decir que si yo tomo un elemento cualquiera del conjunto, entonces puedo encontrar otro elemento del conjunto de tal manera que al operar ambos, el resultado que obtengo es el elemento neutro: .
El concepto de grupo no es invención de Klein, pero es él quien descubre un hecho fundamental que lo relaciona con las distintas geometrías: cada geometría es el estudio de ciertas propiedades que no cambian cuando se le aplican un tipo de transformaciones. Esas propiedades, por no cambiar, las denomina invariantes, y las transformaciones que a un invariante no le hacen cambiar han de tener estructura de grupo bajo la operación de composición (componer dos transformaciones es hacer una de ellas y aplicarle la otra transformación al resultado de la primera). Resumiendo, Klein define soterradamente una geometría como dar el subgrupo de las biyecciones de un conjunto en sí mismo que uno admitirá como grupo principal. Los conceptos o definiciones serán los invariantes por ese grupo principal, y los teoremas serán las relaciones entre los conceptos.
Así Klein descubre que, por ejemplo, la geometría euclidiana es el estudio de los invariantes mediante el grupo de los movimientos rígidos (como las simetrías, giros y traslaciones), que la geometría afín es el estudio de los invariantes mediante el grupo de las translaciones, que la geometría proyectiva es el estudio de los invariantes mediante el grupo de las proyectividades, e incluso que la Topología es el estudio de los invariantes mediante el grupo de las funciones continuas y de inversa continua, entre otras.
De hecho, Klein afirma que la comprensión de "tener una geometría, entonces hay un grupo principal" es más bien al revés. Uno a priori dice qué tipo de transformaciones admitirá (es decir, da el grupo) y todo lo demás se puede reconstruir a partir de él. Se demuestra incluso, que si uno da un subgrupo de las biyecciones de un conjunto en sí mismo isomorfo a algún grupo clásico (simetrías, translaciones, proyectividades) entonces todos los teoremas de esa geometría son válidos en este.
El descubrimiento de Klein es fundamental, ya que por un lado nos permite clasificar las geometrías, comprendiendo cuál es una "subgeometría" de cual, por otro lado nos permite comprender qué es el estudio general de la Geometría (como disciplina matemática) y por último, pero no menos importante, es la confirmación de que los métodos sintético y algebraico no dan geometrías distintas, sino que realmente estudian la misma geometría en cada caso. Se pone fin así a la distinción entre el método sintético y el algebraico-analítico. En su época supuso la consagración de la Geometría proyectiva como la Reina de las Geometrías.
Véase también[editar]
Referencias[editar]
- ↑ Baldor, Gaaplex (2014). Geometría plana y del espacio y trigonometría. México: publicaciones cultural. ISBN 978-8435700788.
- ↑ Wolchover, Natalie (17 de septiembre de 2013). «Physicists Discover Geometry Underlying Particle Physics | Quanta Magazine». Quanta Magazine. Consultado el 20 de febrero de 2017.
- ↑ Neugebauer, 1969, p. 36.
- ↑ «Babylonian Pythagoras». Maths History (en inglés). Consultado el 17 de octubre de 2023.
- ↑ «Babylonian mathematics». Maths History (en inglés). Consultado el 17 de octubre de 2023.
- ↑ «Los babilonios calculaban con triángulos antes que Pitágoras». 4 de agosto de 2021.
- ↑ Kim Plofker (2009). Matemáticas en la India. Princeton University Press. pp. 17–18. ISBN 978-0-691-12067-6. Parámetro desconocido
|title-link=ignorado (ayuda) - ↑ Carl Benjamin Boyer; Uta C. Merzbach (2011). «China and India». A history of mathematics (3rd edición). Wiley. p. 229. ISBN 978-0470525487. «Quote: [In Sulba-sutras,] we find rules for the construction of right angles by means of triples of cords the lengths of which form Pythagorean triages, such as 3, 4, and 5, or 5, 12, and 13, or 8, 15, and 17, or 12, 35, and 37. Although Mesopotamian influence in the Sulvasũtras is not unlikely, we know of no conclusive evidence for or against this. Aspastamba knew that the square on the diagonal of a rectangle is equal to the sum of the squares on the two adjacent sides. Less easily explained is another rule given by Apastamba – one that strongly resembles some of the geometric algebra in Book II of Euclid's Elements. (...)».
- ↑ (Hayashi, 2003, pp. 121–122)
- ↑ Needham, Volume 3, 99.
- ↑ Needham, Volume 3, 101.
- ↑ Needham, Volumen 3, 22.
- ↑ Needham, Volumen 3, 21.
- ↑ Needham, Volumen 3, 100.
- ↑ Needham, Volumen 3, 98-99.
- ↑ Otros atribuyen la paternidad del descubrimiento a Descartes. Cfr. M. De Jonquières, Note sur un Mémoire de Descartes longtemps inédit, et sur les titres de son auteur à la priorité d'une découverte dans la théorie des polyèdre, Académie des sciences (France). Comptes rendus hebdomadaires des séances de l'Académie des sciences. 1835. 1890 (T. 110). p261-266
- ↑ S.A.J. L' Huillier, Mémoire sur la polyédrométrie, contenant une démonstration directe du théorème d'Euler sur les polyèdres et un examen des diverses exceptions auxquelles ce théorème est assujetti, annales de mathématiques pures et appliquées, 1812-13
- ↑ C.F. Gauss, Disquisitiones generales circa superficies curvas, 1827
- ↑ Saccheri, Euclides ab omni naevo vindicatus, 1733
- ↑ Véase O'Connor, John J.; Robertson, Edmund F., «Johann Carl Friedrich Gauss» (en inglés), MacTutor History of Mathematics archive, Universidad de Saint Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Gauss.html.
Bibliografía[editar]
- Baldor, Dr. J. A. (2001) [1983]. Geometría Plana y Del Espacio y Trigonometría (Décima Séptima Reimpresión, México 2001 edición). Miami Florida: Públicaciones Cultural. ISBN 968-439-214-1.
Enlaces externos[editar]
 Wikcionario tiene definiciones y otra información sobre geometría.
Wikcionario tiene definiciones y otra información sobre geometría.- Historia de la Geometría Griega










![{\displaystyle \mathbb {R} [x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de78aea249c4a765d912587db125dfdbacc3d432)






















